判断题(3分一个)
1 向量范数的计算
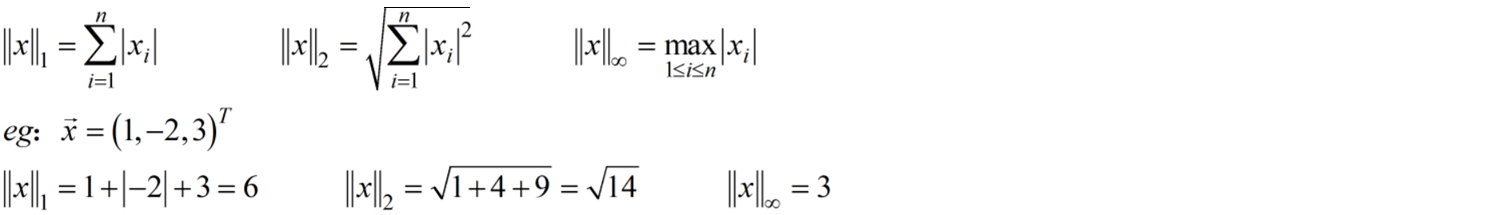
2 矩阵范数的计算

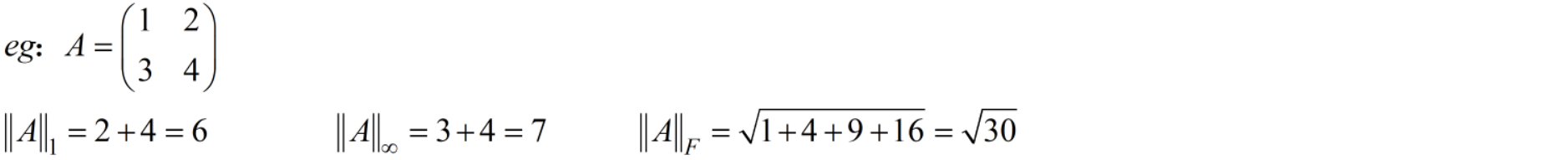
3 给个矩阵,求不变因子【第三章】
若给的矩阵A不是Smith标准形,则需要将λI−AλI-AλI−A初等变换成Smith标准形后再计算不变因子
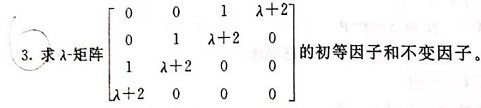

4 矩阵的谱半径的计算
注:是小于等于任意一种范数

5 给个矩阵,判定它是否收敛。


计算题
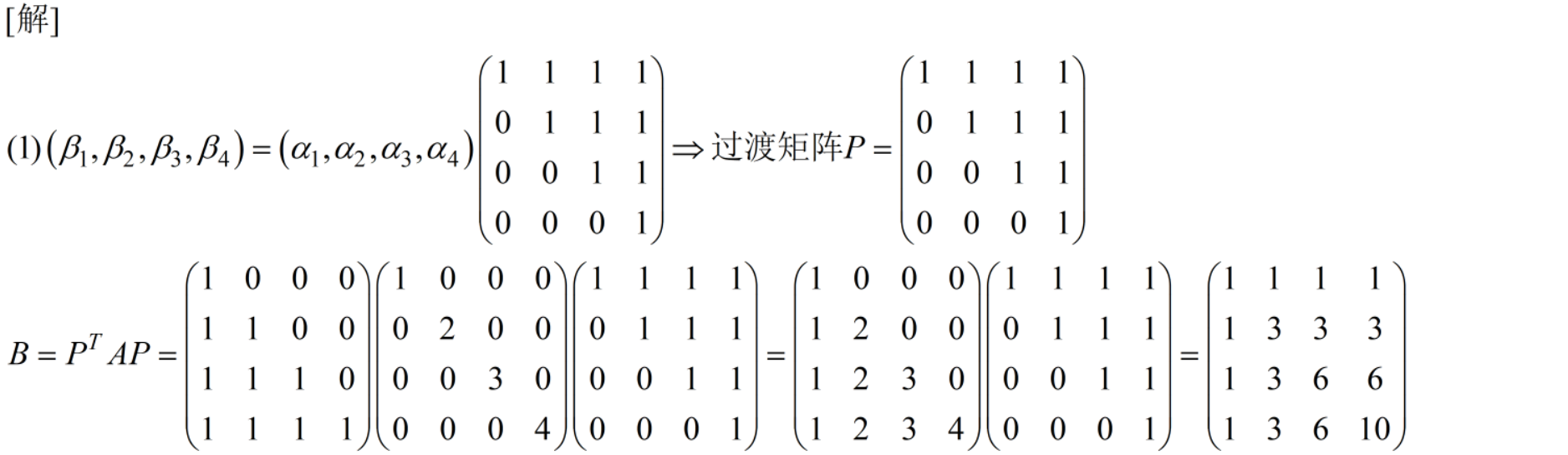
6 求一组基到另一组基的过渡矩阵,并求某一元素在某组基下的坐标。12分【第一章】


求过渡矩阵 :先设过渡矩阵为P,再取简单基后将题给的基都用简单基表示,接着化简代入其中一个式子,使其表示为AP=B的形式。注意题给的是矩阵基,二维矩阵基有4个元素,每个基的元素是以Z字形竖着写成向量样式组成的矩阵。
求坐标:设出坐标后直接线性表示出来。


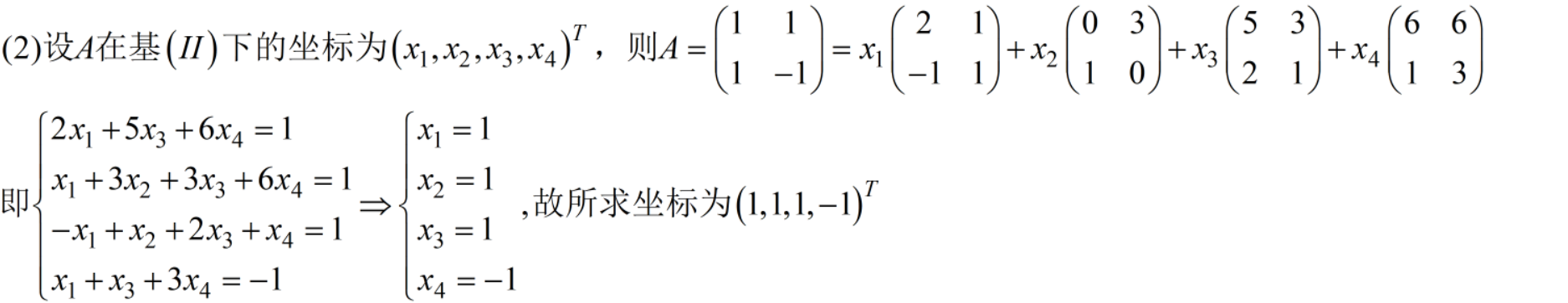
7(1)在线性空间当中定义某一个内积,知道某一组基下的度量矩阵,去求另一组基上的度量矩阵,(2)确定参数使两向量正交。12分【第二章】只用看P31页



8 求Jordan标准型及相似变换矩阵P,注意!会出现无解的情况。12分【第三章】



9 QR分解。12分【第四章】

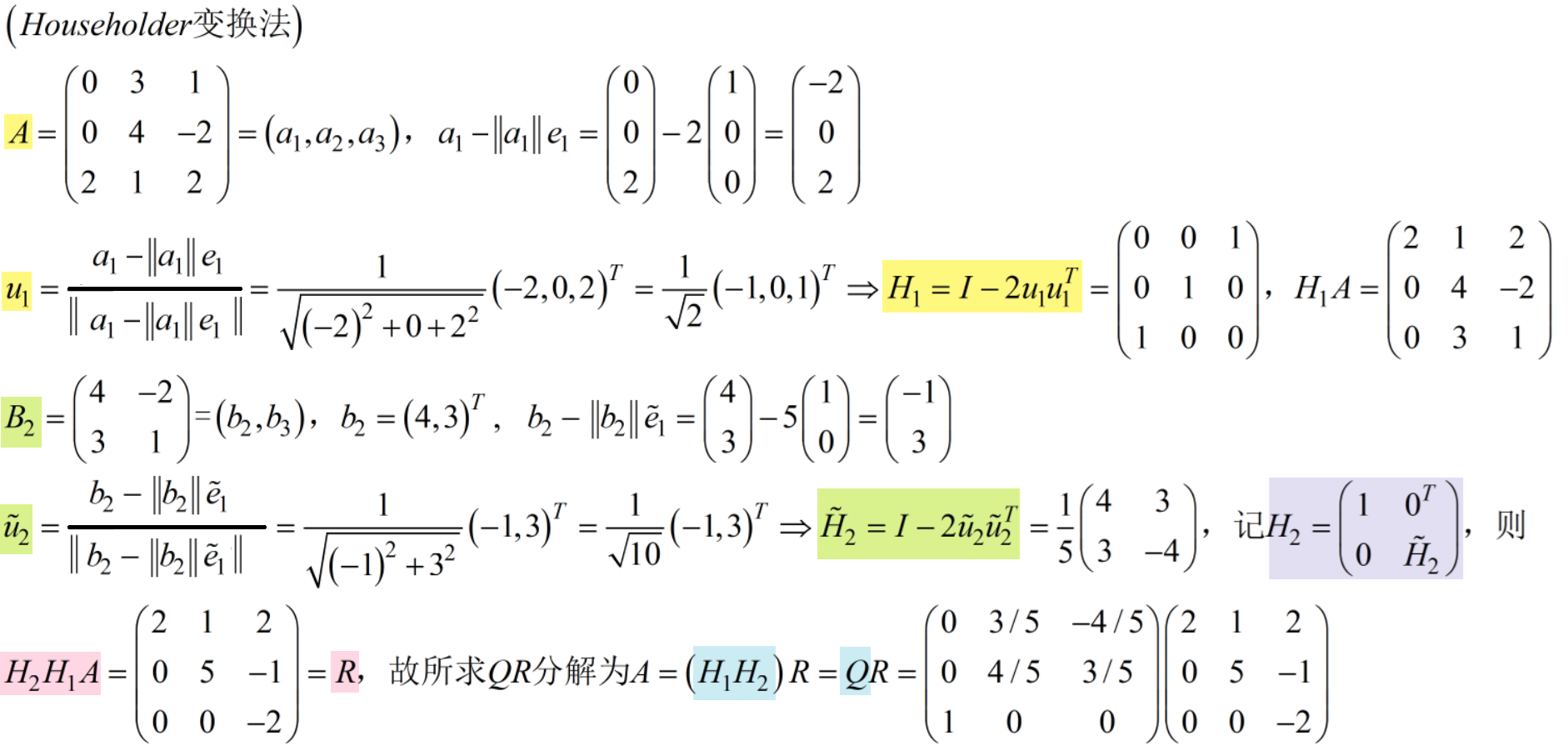
10 判定矩阵幂级数的敛散性,如果收敛,求和。7分
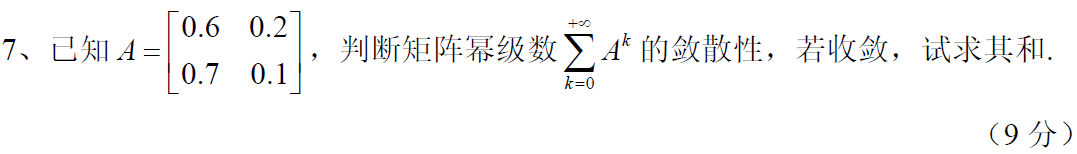
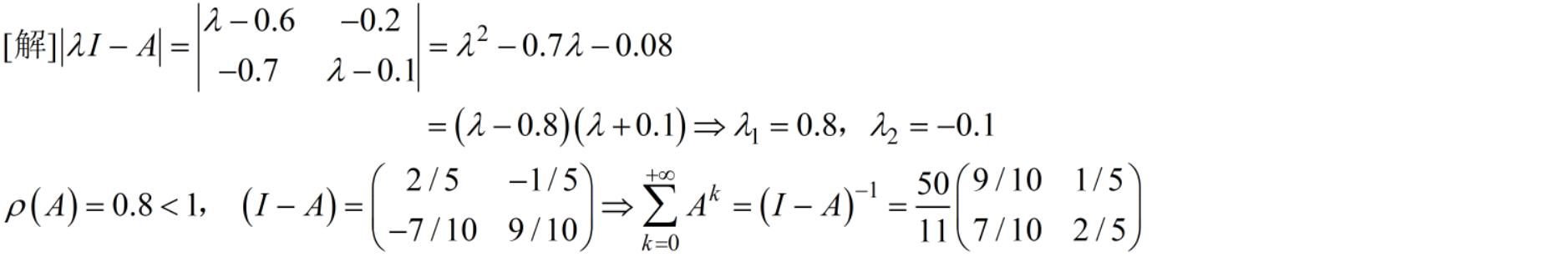
11 求e的At次幂,sinAt,cosAt。15分

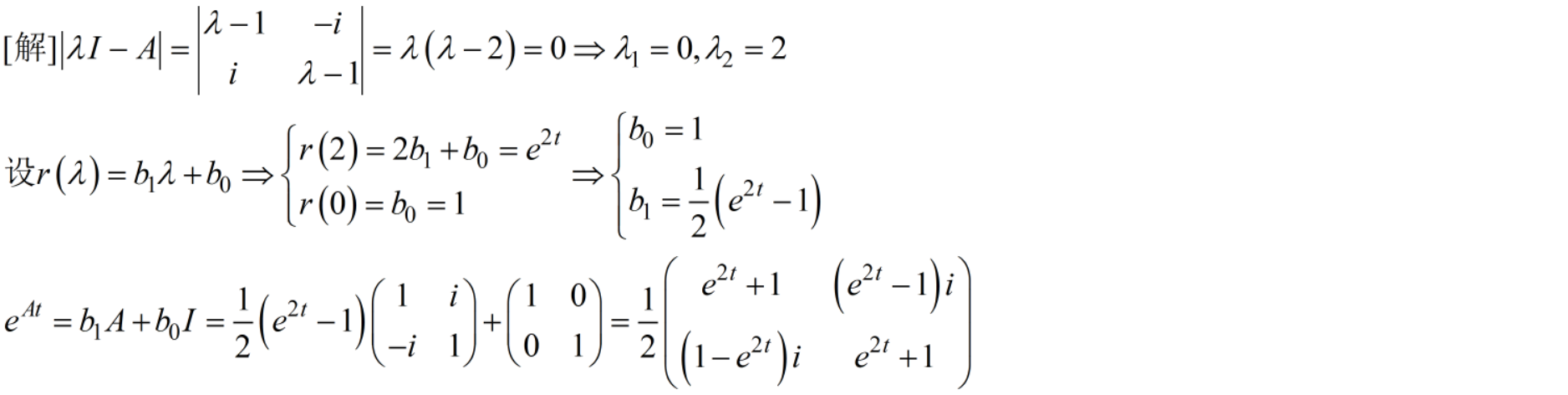
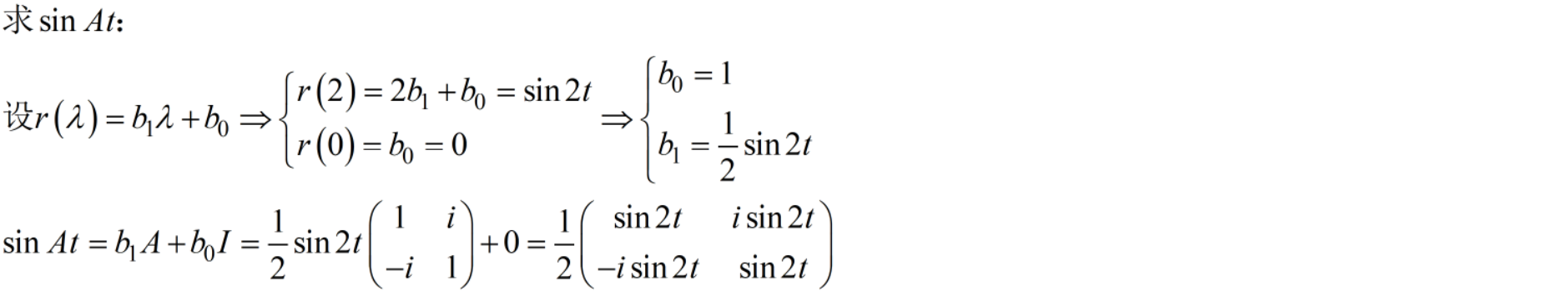
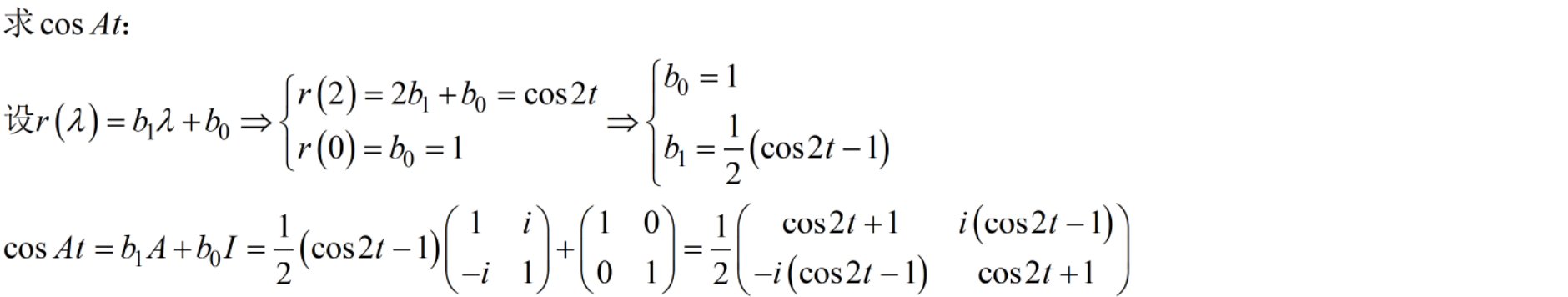

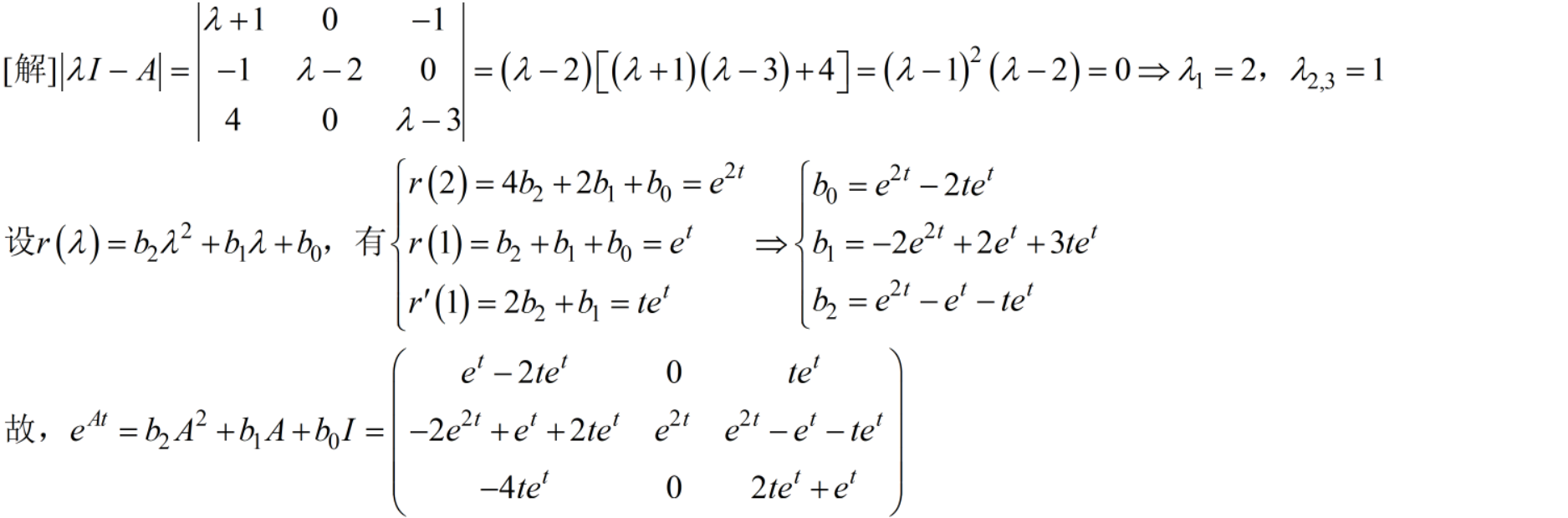
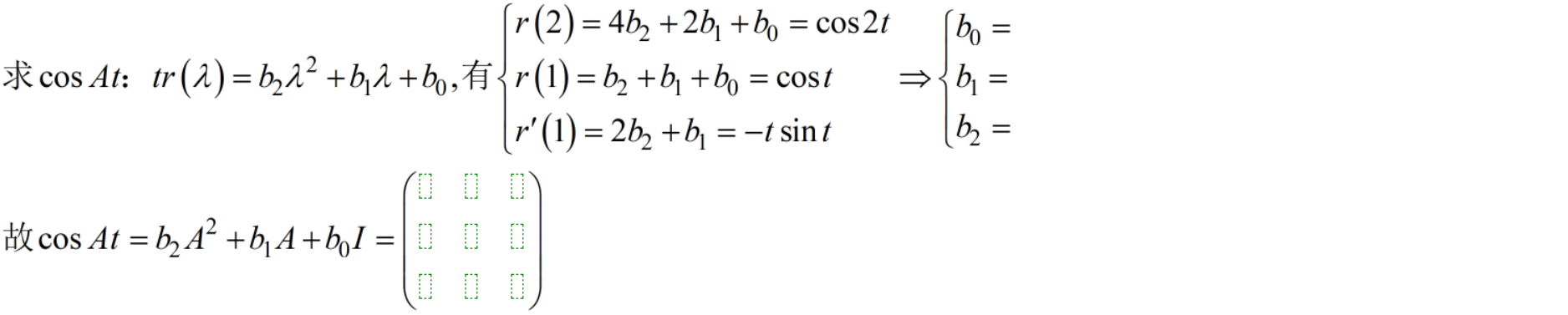
12 求满足初始条件的微分方程组的解。15分
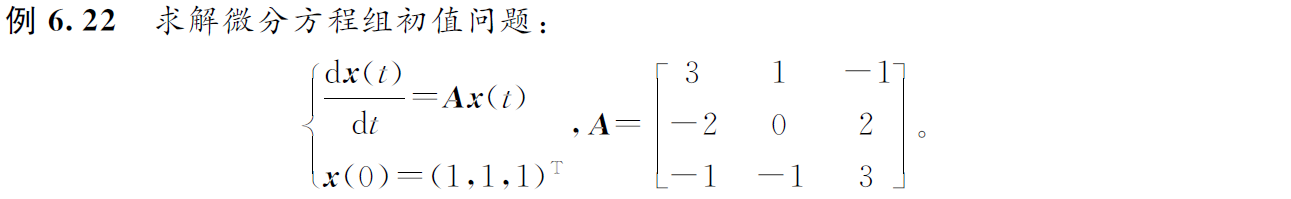
解

