[数字信号处理-入门] 频域分析
个人导航
知乎:https://www.zhihu.com/people/byzh_rc
CSDN:https://blog.csdn.net/qq_54636039
注:本文仅对所述内容做了框架性引导,具体细节可查询其余相关资料or源码
参考文章:各方资料
文章目录
- [[数字信号处理-入门] 频域分析](#[数字信号处理-入门] 频域分析)
- 个人导航
- DTFT和DFT
-
-
-
- [1. DTFT](#1. DTFT)
- [2. DFT](#2. DFT)
- [ZT -> DTFT -> DFT](#ZT -> DTFT -> DFT)
- [∣ X ( e j w ) ∣ − w |X(e^{jw})| - w ∣X(ejw)∣−w频谱图](#∣ X ( e j w ) ∣ − w |X(e^{jw})| - w ∣X(ejw)∣−w频谱图)
-
-
- DFT性质
- FFT
-
-
-
- [1. W N k n W_N^{kn} WNkn性质](#1. W N k n W_N^{kn} WNkn性质)
- [2. N点DFT](#2. N点DFT)
- [3. 蝶形运算](#3. 蝶形运算)
-
-
DTFT和DFT
1. DTFT
X ( e j w ) = ∑ n = − ∞ ∞ x ( n ) e − j w n X(e^{jw})=\sum_{n=-\infty}^{\infty} x(n)e^{-jwn} X(ejw)=n=−∞∑∞x(n)e−jwn
DTFT的周期是 2 π 2\pi 2π, w ∈ [ 0 , 2 π ) w \in [0,2\pi) w∈[0,2π)
2. DFT
X ( k ) = ∑ n = 0 N − 1 x ( n ) e − j 2 π N n k x ( n ) = 1 N ∑ k = 0 N − 1 X ( k ) e − j 2 π N k n X(k)=\sum_{n=0}^{N-1} x(n)e^{-j\frac{2\pi}{N}nk} \\ x(n)=\frac{1}{N}\sum_{k=0}^{N-1}X(k)e^{-j\frac{2\pi}{N}kn} X(k)=n=0∑N−1x(n)e−jN2πnkx(n)=N1k=0∑N−1X(k)e−jN2πkn
将DTFT的 w w w做N等分取样, 其取值就是DFT
也可以说是ZT的单位圆的N等分点
ZT -> DTFT -> DFT
| ZT | DTFT | DFT |
|---|---|---|
| X ( z ) X(z) X(z) | X ( e j w ) X(e^{jw}) X(ejw) | X ( k ) X(k) X(k) |
| ∑ n = − ∞ ∞ x ( n ) z − n \sum_{n=-\infty}^{\infty}x(n)z^{-n} ∑n=−∞∞x(n)z−n | ∑ n = − ∞ ∞ x ( n ) e − j w n \sum_{n=-\infty}^{\infty} x(n)e^{-jwn} ∑n=−∞∞x(n)e−jwn | ∑ n = 0 N − 1 x ( n ) e − j 2 π N n k \sum_{n=0}^{N-1} x(n)e^{-j\frac{2\pi}{N}nk} ∑n=0N−1x(n)e−jN2πnk |
- ZT -> DTFT: z = e j w z=e^{jw} z=ejw
- DTFT -> DFT: w=\\frac{2\\pi}{N}k,\\quad k=0,...,N-1, w \\in \[0,2\\pi)
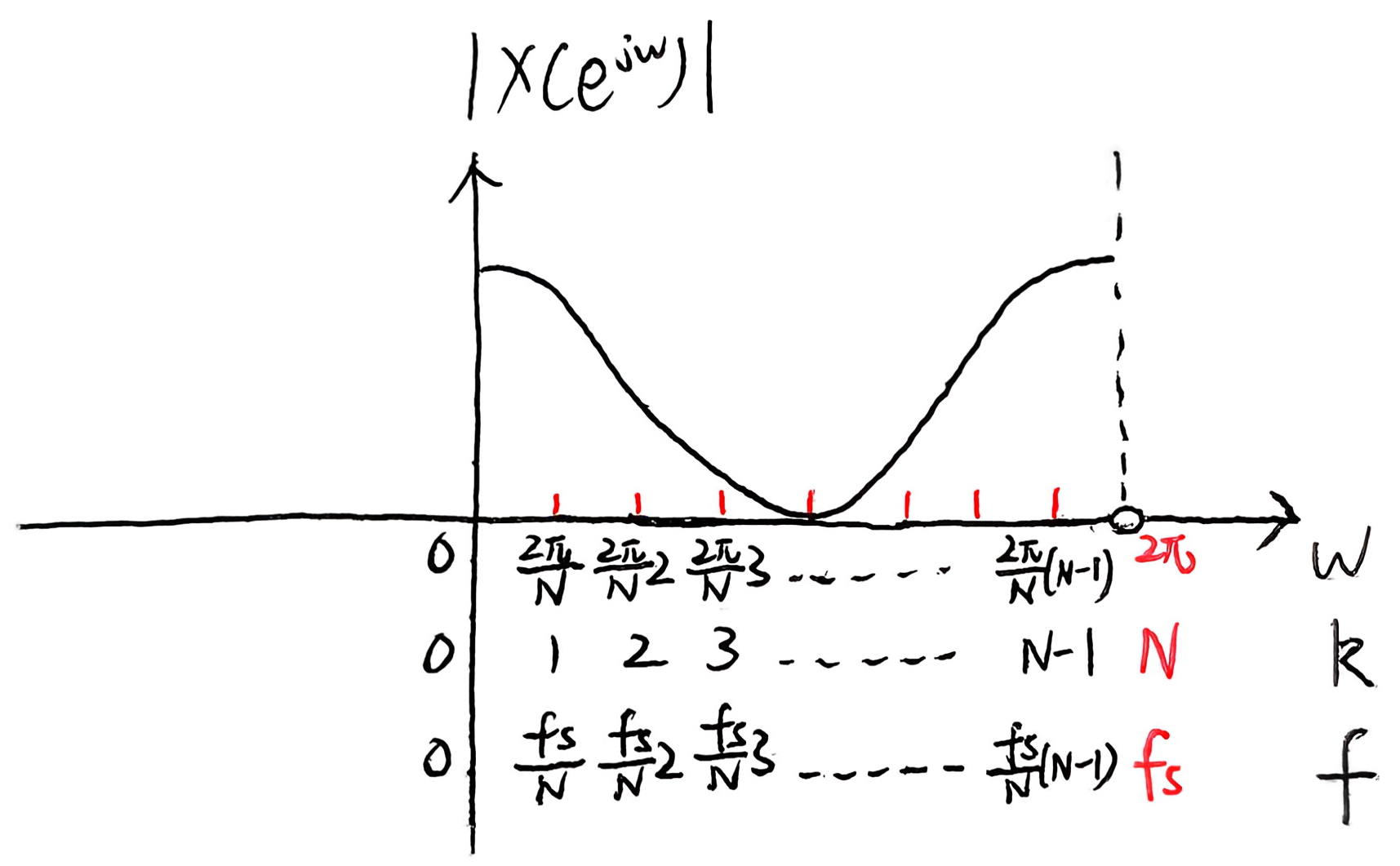
∣ X ( e j w ) ∣ − w |X(e^{jw})| - w ∣X(ejw)∣−w频谱图
- X ( k ) X(k) X(k)对应 w = 2 π N ⋅ k w=\frac{2\pi}{N}\cdot k w=N2π⋅k的点
- 当 w w w接近 2 π 2\pi 2π时
- 若换做 f f f(Hz)做横轴, 则 f f f接近 f s f_s fs
- 若换做 k k k做横轴, 则 k k k接近 N N N
- 频率分辨率: △ f = f s / N \triangle f =f_s/N △f=fs/N
DFT性质
1.循环卷积
用DFT来求解线性卷积
因为有FFT可以帮DFT快速运算
假设循环卷积的点数是 L L L点的, 线性卷机两个序列长度是 N 1 N_1 N1和 N 2 N_2 N2
当 L ≥ N 1 + N 2 − 1 L \geq N_1+N_2-1 L≥N1+N2−1时, 可以取循环卷积的主值区域
循环卷积就是线性卷积以 L L L为周期做周期延拓
2.分析信号频谱
频率分辨率:
△ f = f s / N = 1 / T 0 \triangle f =f_s/N=1/T_0 △f=fs/N=1/T0
1 / T 0 1/T_0 1/T0: 数据的长度的倒数
工程问题的理解分析:
- f s f_s fs如何避免混叠 -> f s ≥ 2 f h f_s \geq 2f_h fs≥2fh
- 采样定理要求的信号需要是频带有限信号 -> 时域无限长
- 工程上需要给时域无限长信号加窗
时域加窗(时域相乘) -> 频域卷积 -> 展宽信号的频谱
(展宽的程度受窗函数的主瓣宽度的影响) - 旁瓣干扰 -> 频谱泄漏, 谱间串扰
FFT
DFT:
X ( k ) = ∑ n = 0 N − 1 x ( n ) e − j 2 π N n k = ∑ x ( n ) W N n k W N = x ( n ) e − j 2 π N X(k)=\sum_{n=0}^{N-1} x(n)e^{-j\frac{2\pi}{N}nk}=\sum x(n)W_N^{nk} \\ W_N = x(n)e^{-j\frac{2\pi}{N}} X(k)=n=0∑N−1x(n)e−jN2πnk=∑x(n)WNnkWN=x(n)e−jN2π
1. W N k n W_N^{kn} WNkn性质
-
周期性 W N n k = W N ( n + N ) k = W N n ( k + N ) W_N^{nk}=W_N^{(n+N)k}=W_N^{n(k+N)} WNnk=WN(n+N)k=WNn(k+N)
-
共轭对称性 ( W N n k ) ∗ = W N − n k (W_N^{nk})^*=W_N^{-nk} (WNnk)∗=WN−nk
-
可约性 W N n k = W m N m n k W_N^{nk}=W_{mN}^{mnk} WNnk=WmNmnk, W N m k = W N / m n k \ W_N^{mk}=W_{N/m}^{nk} WNmk=WN/mnk
2. N点DFT
- 乘法: N 2 N^2 N2
- 加法: N ( N − 1 ) N(N-1) N(N−1)
-> 希望把 N N N减小
时域抽取: 基2-DIT
频域抽取: 基2-FIT
3. 蝶形运算
共L级
N = 2 L L = log 2 N N=2^L \\ L=\log_2 N N=2LL=log2N
每一级有 N / 2 N/2 N/2个蝶形
每一个蝶形, 乘1次, 加2次
-> 乘法共有 N 2 log 2 N \frac{N}{2}\log_2N 2Nlog2N, 加法共有 2 N 2 log 2 N 2\frac{N}{2}\log_2N 22Nlog2N