
A股涨到3600点了。
你是不是也跟我一样------看到新闻标题说"牛市要来了!",一打开账户......嗯?怎么手里的票还是绿的,上证指数25年都涨7%了,而你确亏了7%

为什么你的股票没涨过大盘?到底是市场的问题,还是你的股票压根不跟着市场走?
聪明的你可能已经想到一个词了,叫------β值(Beta)。
说白了,β值其实就是个股相对大盘"跟涨跟跌"的敏感度。你可以把它想象成你手上这票对"市场情绪"的反应速度和强度。
- β > 1 的股票,市场一疯,它先蹦跶;市场一跌,它先躺平。
- β < 1 的股票,属于佛系型,涨跌都慢半拍。
- β ≈ 0 的,那是独行侠,走自己的路让别人说去吧。
我知道,有些小伙伴可能说:"花姐你说这我都懂,但怎么算这个β值啊?"
来,今天我们就来整点硬核的------用卡尔曼滤波器来动态估算β值。
传统β值是怎么算的?
这事儿咱得先交代清楚,不然后面你会问:为啥要搞卡尔曼滤波呢?直接用回归不香吗?
最常见的β值计算方式是用OLS线性回归,比如拿某个股票和上证指数近一年日收益率,做个线性回归,斜率就是β值。代码长这样:
python
import pandas as pd
import numpy as np
import statsmodels.api as sm
stock_ret = ... # 股票收益率序列
market_ret = ... # 市场指数收益率序列
X = sm.add_constant(market_ret)
model = sm.OLS(stock_ret, X).fit()
beta = model.params[1]结果算出来的β是固定的一个值 。问题来了:市场在变,个股特性也在变,一个固定的β能代表未来吗?
用卡尔曼滤波器
那么问题来了:有没有什么办法,可以让β值随着时间动态变化,反映出最新的市场行为?
有!这时候就该请出我们的主角了------卡尔曼滤波器(Kalman Filter)。
别听名字吓人,其实你可以把它理解为一个"会自我更新"的预测模型。它有点像是个不断修正自己认知的智能体,每来一个新数据,就纠正一下之前的偏差。
如果说OLS是一次性静态判断,那卡尔曼滤波就是边走边看边修正。
卡尔曼滤波器怎么估算β?
卡尔曼滤波在量化里的用途很多,其中一个经典用途就是:时间序列中的线性参数动态估计。
我们的问题就可以建模成这个样子
股票收益率 = α + β × 市场收益率 + 噪声
不同的是,我们让β变成一个随时间变化的变量。 也就是说,今天的β和昨天的不一样,明天的也不一定一样。
我们设定两个方程:
状态方程(β的演变):
<math xmlns="http://www.w3.org/1998/Math/MathML"> β t = β t − 1 + w t β_t = β_{t-1} + w_t </math>βt=βt−1+wt
观测方程(收益率的观察):
<math xmlns="http://www.w3.org/1998/Math/MathML"> y t = α + β t ∗ x t + v t y_t = α + β_t * x_t + v_t </math>yt=α+βt∗xt+vt
其中:
- <math xmlns="http://www.w3.org/1998/Math/MathML"> x t x_t </math>xt 是大盘的收益率
- <math xmlns="http://www.w3.org/1998/Math/MathML"> y t y_t </math>yt 是股票的收益率
- <math xmlns="http://www.w3.org/1998/Math/MathML"> w t w_t </math>wt 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> v t v_t </math>vt 是噪声,分别表示系统噪声和观测噪声
这个模型的核心点是:我们认为β本身在缓慢变化,而每个观测数据都能对β的估计做一次修正。
不扯了,直接上代码!
咱们用 Python 写个计算个股β值的方法,当然你也可以把上证指数换成股票对应的行业指数,这样就可以得到个股相对行业的β值了。
这里计算卡尔曼的时候用了第三方库通过以下代码安装
txt
pip install pykalman
python
from xtquant import xtdata
import pandas as pd
from pykalman import KalmanFilter
import numpy as np
import matplotlib.pyplot as plt
def get_hq(code,start_date='19900101',period='1d',dividend_type='front',count=-1):
'''
这里替换成你获取行情的方法
'''
df = pd.read_csv(f'{code}.csv')
return df
def calu_kalman_beta(df_stock,df_index):
'''
计算某个股票相对某个指数的β值
'''
# 对齐日期,按日期升序
df_stock = df_stock.sort_values('date')
df_index = df_index.sort_values('date')
df_stock = df_stock[df_stock['suspendFlag'] == 0] # 剔除停牌数据
# 合并,方便对齐(外层用 inner,保证两个都有数据)
df = pd.merge(df_stock[['date', 'close']],
df_index[['date', 'close']],
on='date',
suffixes=('_stock', '_index'))
# 计算对数收益率(更平滑、更合理)
df['ret_stock'] = np.log(df['close_stock'] / df['close_stock'].shift(1))
df['ret_index'] = np.log(df['close_index'] / df['close_index'].shift(1))
# 去除缺失
df = df.dropna().reset_index(drop=True)
# 提取序列
stock_ret = df['ret_stock'].values
index_ret = df['ret_index'].values
# 初始化卡尔曼滤波器
kf = KalmanFilter(
transition_matrices=1.0,
observation_matrices=1.0 ,
initial_state_mean=0.0,
initial_state_covariance=1.0,
observation_covariance=0.01, # 控制对观测数据的信任度 可微调
transition_covariance=0.00001 # 控制 β 的平滑程度 越小越平滑
)
# 加入极端值裁剪(防止除以接近0)
index_ret_safe = np.where(np.abs(index_ret) < 1e-4, np.sign(index_ret) * 1e-4, index_ret)
# 我们把 market_ret 作为"输入变量",用于动态预测观测值
observations = stock_ret / index_ret_safe # y_t / x_t
observations = np.clip(observations, -10, 10) # 避免除数太小导致爆炸(你也可以换个方式)
state_means, _ = kf.filter(observations)
df['beta_kalman'] = state_means.flatten()
return df[10:]
if __name__=="__main__":
start_date='20240101'
code = '这里替换成股票代码'
index = '这里是指数代码'
df_stock = get_hq(code=code,start_date=start_date,period='1d')
df_index = get_hq(code=index,start_date=start_date,period='1d')
df = calu_kalman_beta(df_stock,df_index)
# 画图
plt.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体
plt.rcParams['axes.unicode_minus'] = False # 正负号也正常显示
plt.figure(figsize=(12, 6))
plt.plot(df['date'], df['beta_kalman'], label='动态β(Kalman估计)', color='orange')
plt.axhline(1, linestyle='--', color='gray', alpha=0.5)
plt.title(f'{code} vs {index} 的动态β值')
plt.xlabel('date')
plt.ylabel('β值')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()给大家简单展示几个绘制的图
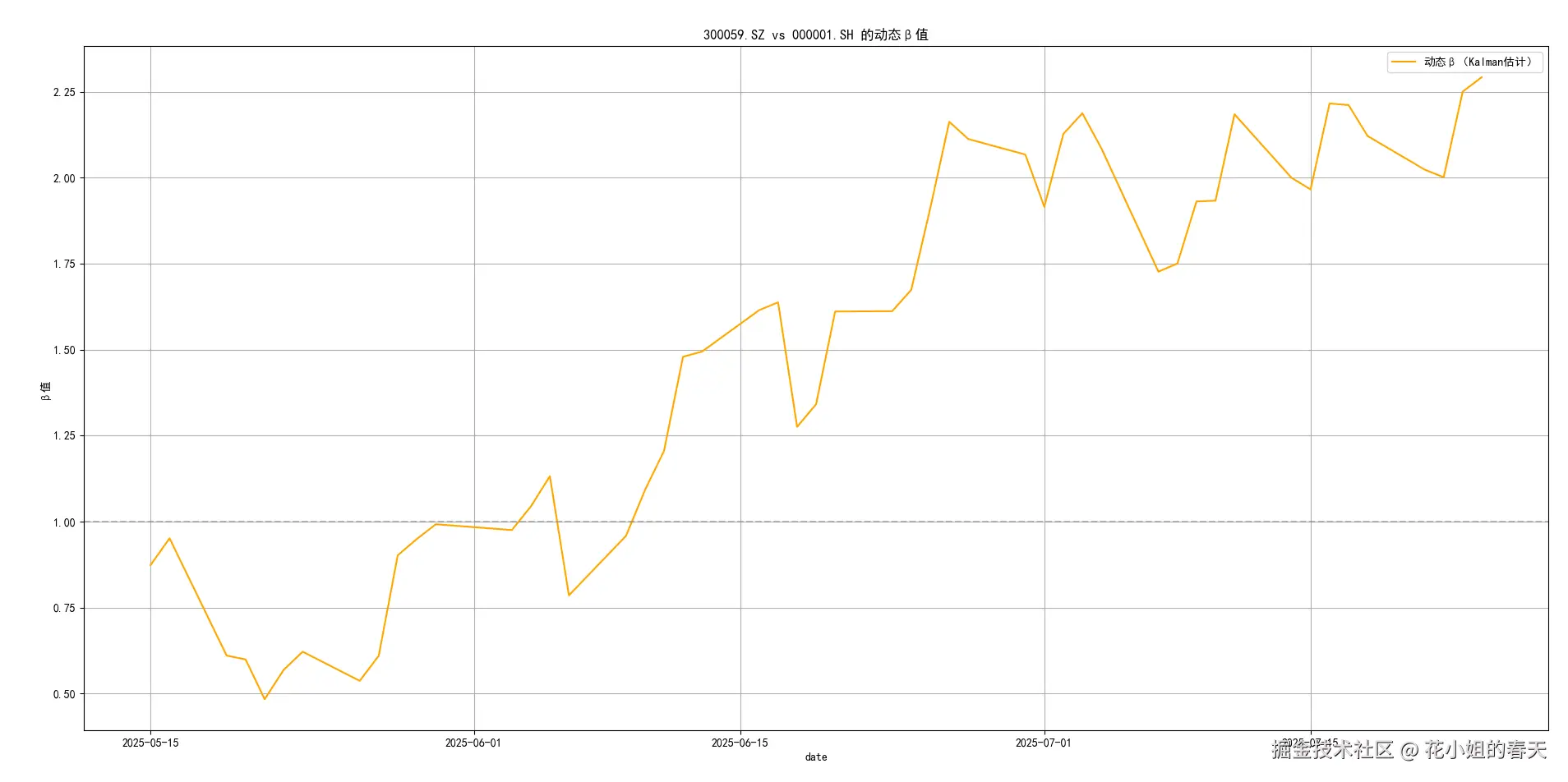
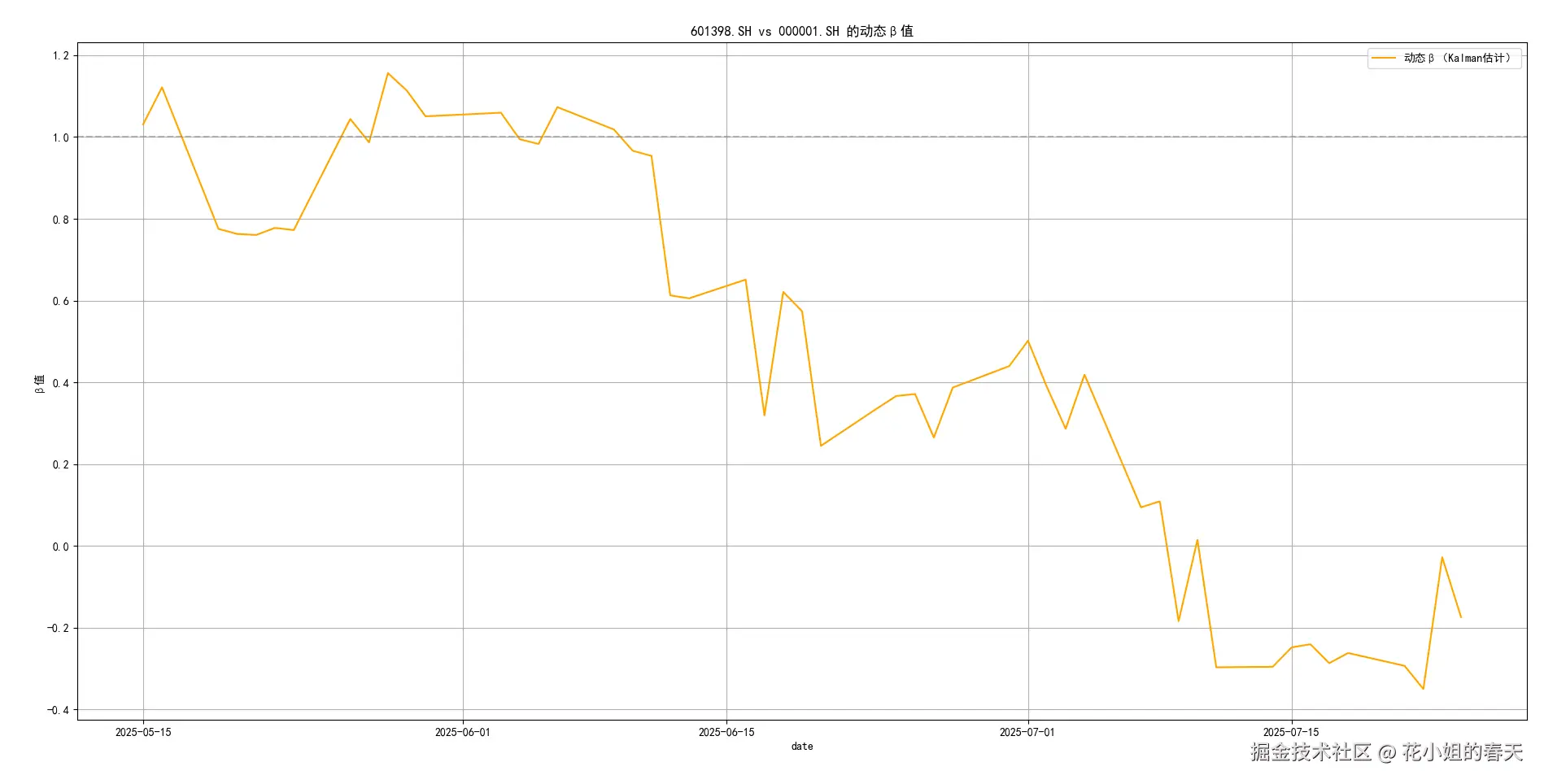
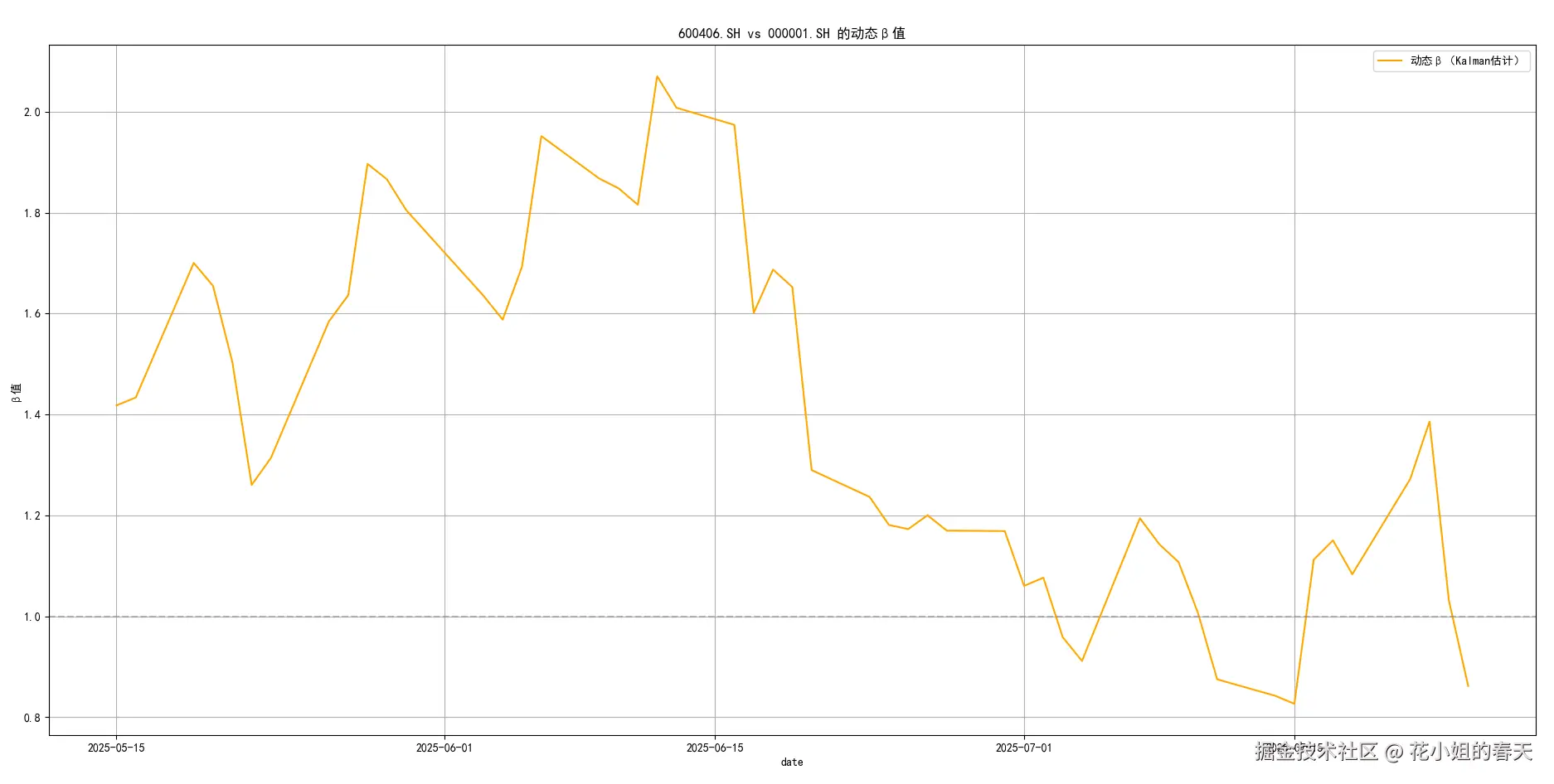
那我怎么用这个β?
有意思的来了。
用法1:选股
找出动态β长期 < 1 的股票,说明它抗跌能力强------在市场波动大的时候更稳。这类票适合熊市配置。
反过来,找动态β > 1.2 并上升中的,说明它在牛市中可能跑得飞快。
你甚至可以把这个β当作因子,搞个多空策略:多β上升的,空β下降的,构建一个方向中性的策略组合。这个思路其实在某些CTA策略里也有影子。
用法2:择时
你还可以跟踪你组合的整体β,动态调整仓位。
举个栗子:你组合的β从0.9升到1.3,说明风险在上升------这时候该减仓。反之也是。
今天的文章就到这里了,希望大家喜欢。