算法竞赛---宽度优先搜索求解最短路径问题

今天主要是学习了这个宽度优先搜索在我们的最短路径问题里面的应用，有些题目是比较模版化的，基本上搞明白其中的一个之后剩下的也是可以写出来的；

但是有些题目是有些困难的，困难的地方在于我们的这个题目无法直接使用这个bfs进行求解，例如晚上的一个题目：颜色的填充问题，我将逐个进行说明和介绍；

1.马的遍历

下面的这个求解的是我们的马儿到棋盘上面的任意的一个点，无论是我们的这个国际象棋还是这个中国象棋，其实这个思路都是类似的；

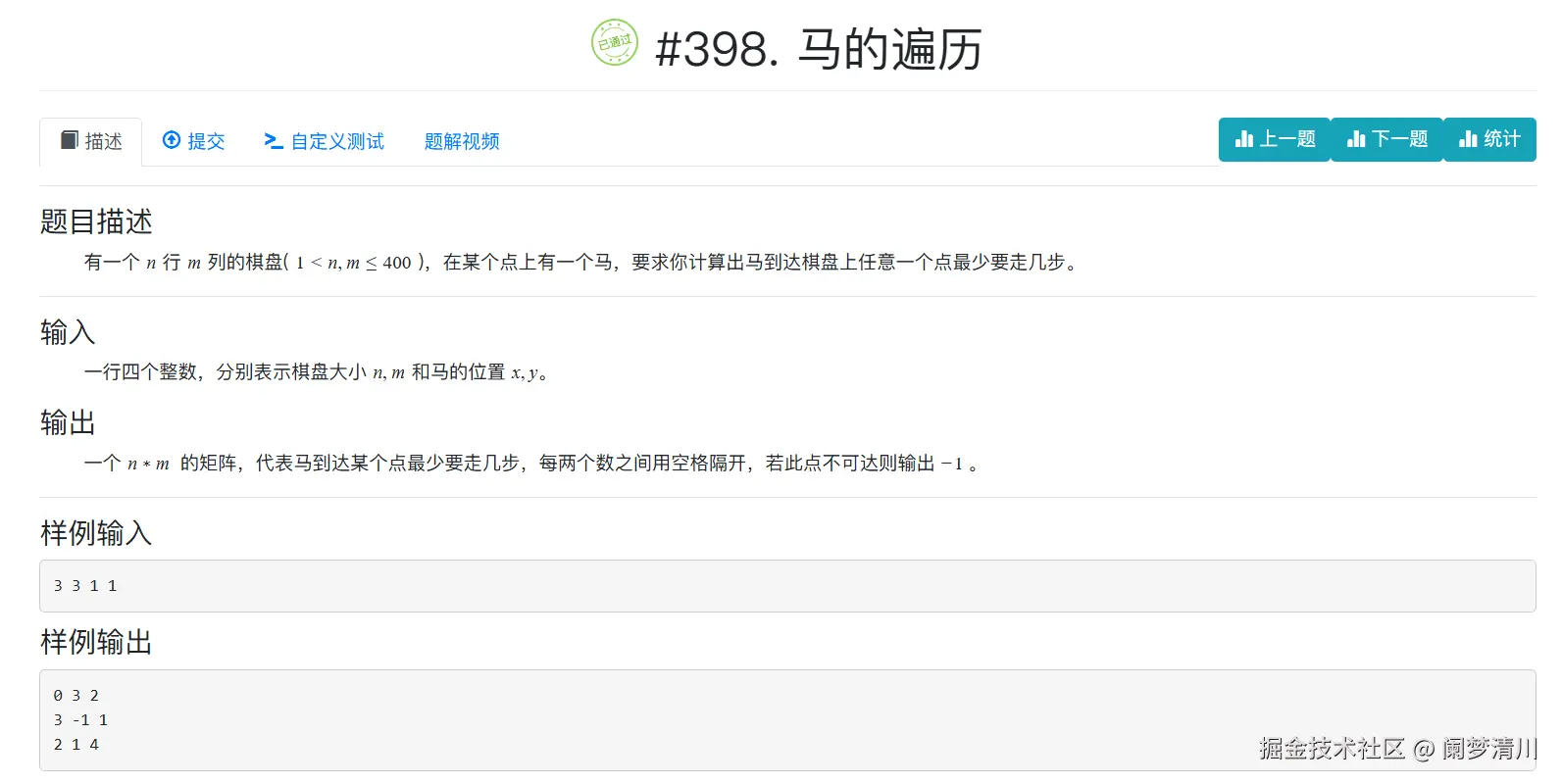
1）这个题目可以说是这个经典的可以使用bfs来求解的这个最短的路径的问题；

2）const N是根据我们的这个题目上面的数据的范围确定的，dist表示的就是我们的距离数组，也就是这个位置具体我们的这个行动开始的位置的距离；

3）dx,dy就是方向数组，根据这个马儿的可以到达的这个方向进行相关的定义的；

4）首先我们分析这个程序，需要从这个代码的主函数，输入的内容就是按照这个题目的要求来的。然后调用我们的宽度优先遍历的这个函数，最后对于这个dist数组里面的内容进行输出即可；

5）对于这个bfs函数里面的逻辑，实际上就是借助队列实现的，我们首先全部置为-1，因为默认情况下是0和我们的题目冲突，题目里面的0表示的是马儿的起始位置；

6）pair其实就是表示的我们的这个位置的下标，也就是遍历到的这个点的横坐标和纵坐标，在这个while循环里面，对于方向数组里面的8个情况进行处理，第一个if保证的是我们的这个遍历的过程当中不可以超出我们的边界；

如果不等于-1，表示这个地方已经跳过了，因此直接忽略即可，也就是continue即可；

7）既没有超出边界，也是属于没有遍历过的，这个时候就是符合条件的，这个新的点的步数就是原来的结果+1即可，并且把这个坐标放到我们的队列里面去；

8）最后就是这个题目里面的独特的需要，需要对于这个空格进行处理，本来是直接输出数字+空格即可，但是这个情况下每一行里面的最后一个元素也是存在这个空格额的，在这个网站上面是不允许这个情况的，因此这个需要进行额外的处理，但是这个限制在其他的诸如洛谷之类的这个网站上面其实不会限制的；

#include <iostream>
#include <queue>
#include <cstring>
​
using namespace std;
​
typedef pair<int, int> PII;
​
const int N = 410;
​
int n, m, x, y;
int dist[N][N];
​
int dx[] = {1, 2, 2, 1, -1, -2, -2, -1};
int dy[] = {2, 1, -1, -2, -2, -1, 1, 2};
​
void bfs()
{
    memset(dist, -1, sizeof dist);
​
    queue<PII> q;
    q.push({x, y});
    dist[x][y] = 0;
​
    while(q.size())
    {
        auto t = q.front(); q.pop();
        int i = t.first, j = t.second;
        for(int k = 0; k < 8; k++)
        {
            int x = i + dx[k], y = j + dy[k];
            if(x < 1 || x > n || y < 1 || y > m) continue;
            if(dist[x][y] != -1) continue;
​
            dist[x][y] = dist[i][j] + 1; // 更细结果
            q.push({x, y});
        }
    }
}
​
int main()
{
    cin >> n >> m >> x >> y;
​
    bfs();
​
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            if(j!=1) cout<<" ";
            cout << dist[i][j];
        }
        cout << endl;
    }
​
    return 0;
}

2.骑士风度的牛

下面的这个题目我应该是花费了两个小时，遇到很多问题，记忆犹新；

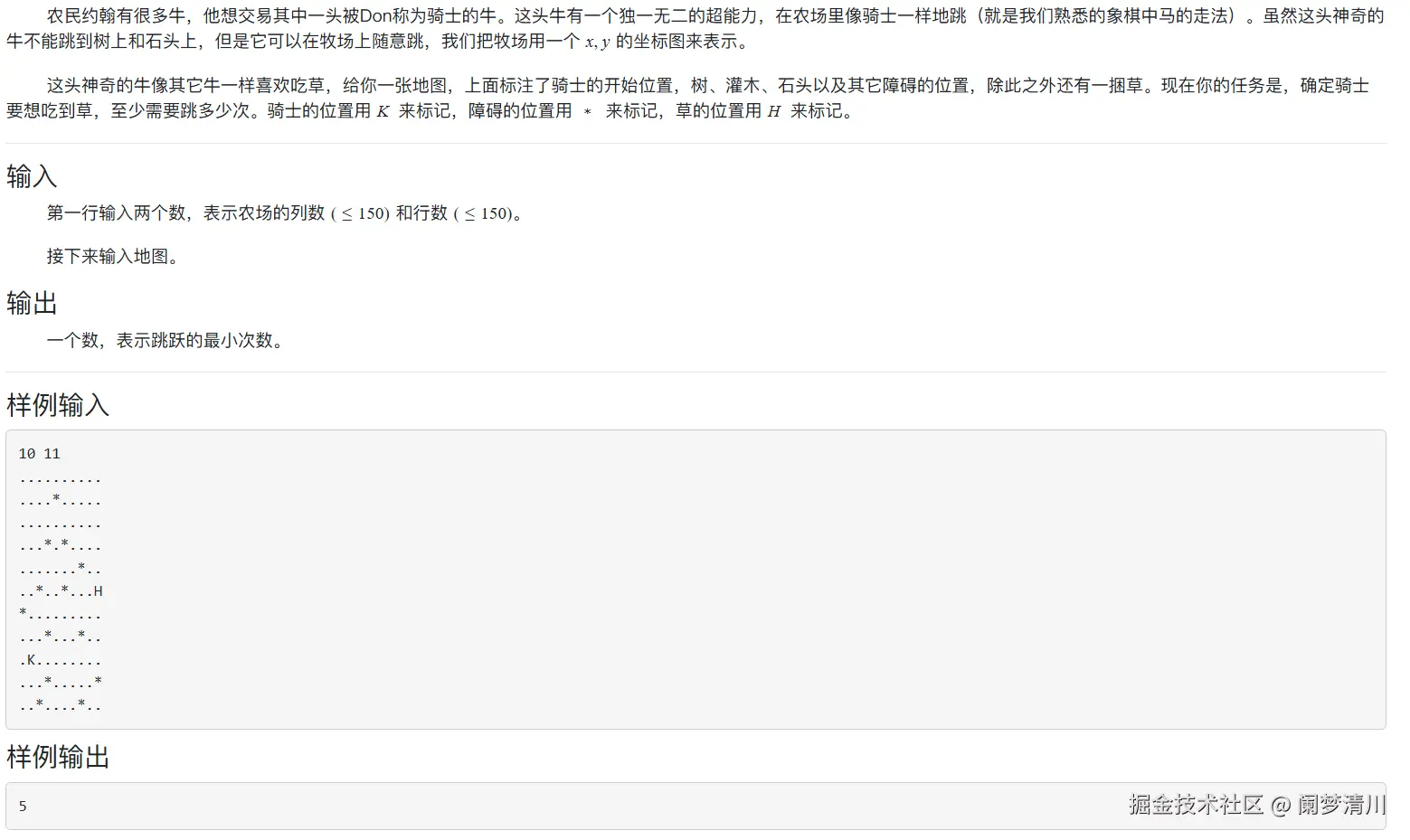
下面的这个就是我们的代码：

1）首先需要注意的就是我们的这个输入的内容，他是先输入列数，再输入行数，这个是非常的坑人的，我刚开始的一个小时都是在处理这个问题，花费了1个小时都是在检查代码逻辑，最后发现是这个输入的问题，这个就是审题的细心的问题啦，花了我1小时，因为刚开始我一直认为是这个代码的逻辑的问题；

2）还有就是刚开始我的这个模拟的过程是按照上下左右的这个顺序来的，后来发现这个事按照象棋里面的这个马顺序来的，因此之前我的这个bfs里面是进行四次循环，口音为上下左右之后4个可能得情况，但是后来成为马的情况下，这个是需要进行8次循环的这个过程的；

3）这个里面的*表示的就是障碍物，因此遇到这个星号的时候需要跳过，其他的还是上面的这个队列的操作，判断的逻辑，边界范围的处理，其他的都是一样的；

#include <iostream>
#include <queue>
#include <cstring>
​
using namespace std;
​
typedef pair<int, int> PII;
​
const int N =155;
​
int n, m, x, y;
char a[N][N];
int dist[N][N];
​
int dx[] = {1, 2, 1, 2,-1,-2,-1,-2};
int dy[] = {2, 1, -2, -1,2,1,-2,-1};
​
void bfs()
{
    memset(dist, -1, sizeof dist);
    queue<PII> q;
    q.push({x, y});
    dist[x][y] = 0;
    
    while(q.size())
    {
        auto t = q.front(); q.pop();
        int i = t.first, j = t.second;
        for(int k = 0; k < 8; k++)
        {
            int x = i + dx[k], y = j + dy[k];
            if(x >= 1 && x <= n && y >= 1 && y <= m && a[x][y] != '*' && dist[x][y] == -1)
            {
                dist[x][y] = dist[i][j] + 1;
                q.push({x, y});
            }
        }
    }
}
​
int main()
{
    cin >> m >> n;
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            cin >> a[i][j];
                //下面的这个表示的就是刚刚开始的位置哈
            if(a[i][j] == 'K')
            {
                x = i; y = j;
            }
        }
    }
    
    bfs();
    
    // 统计结果
    //int cnt = 0, ret = 1e9;
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            if(a[i][j] == 'H' && dist[i][j] != -1)
            {
                //cnt++;
                cout<<dist[i][j]<<endl;
            }
        }
    }
        
    return 0;
}