目录
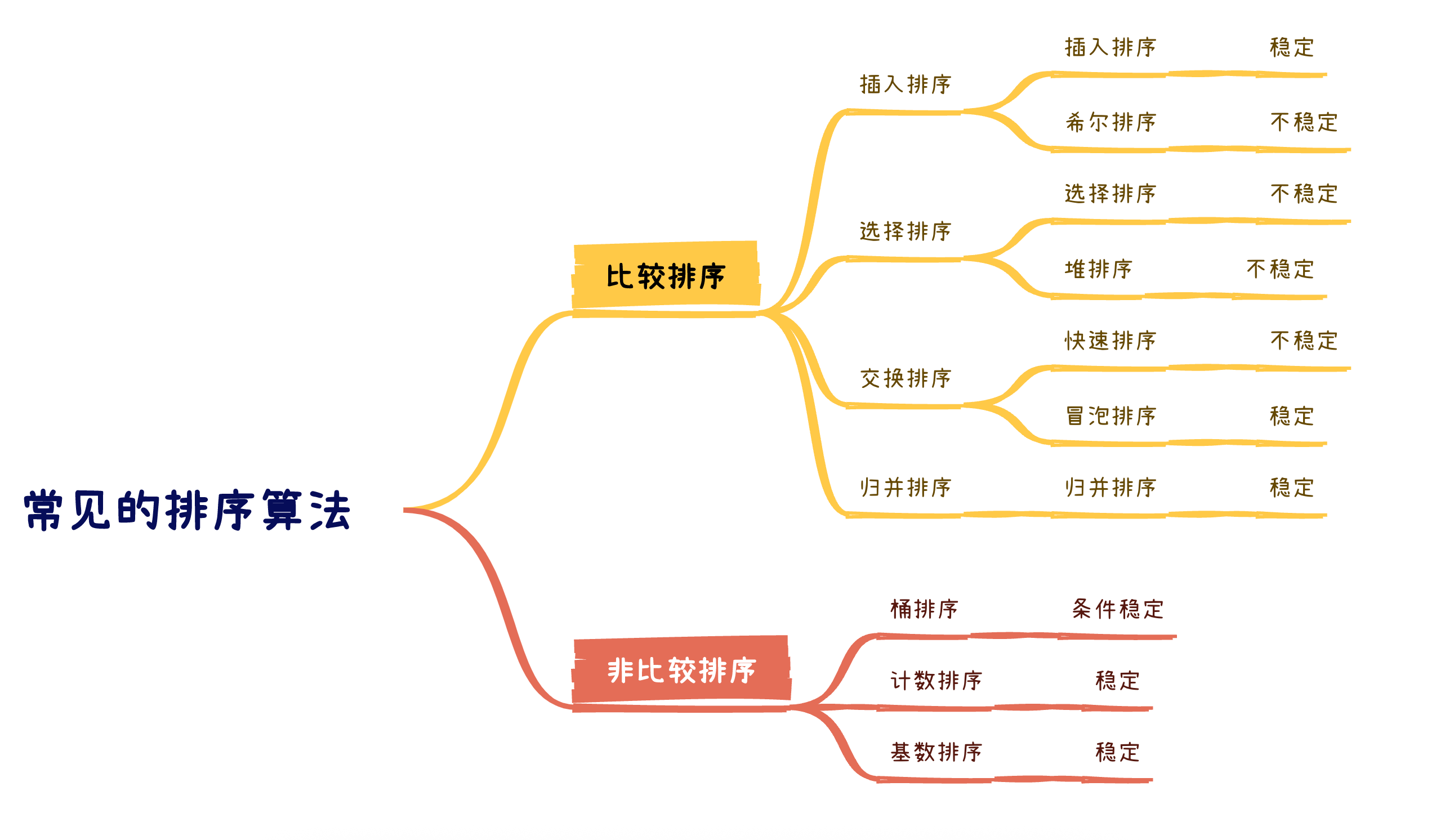
十大算法排序分类
本篇分享十大排序算法中的 需要进行交换操作的归并排序 , 其余算法也有介绍噢:
排序算法---交换排序(冒泡、快速)(动图演示)-CSDN博客
排序算法-选择排序(选择排序、堆排序)(动图演示)-CSDN博客
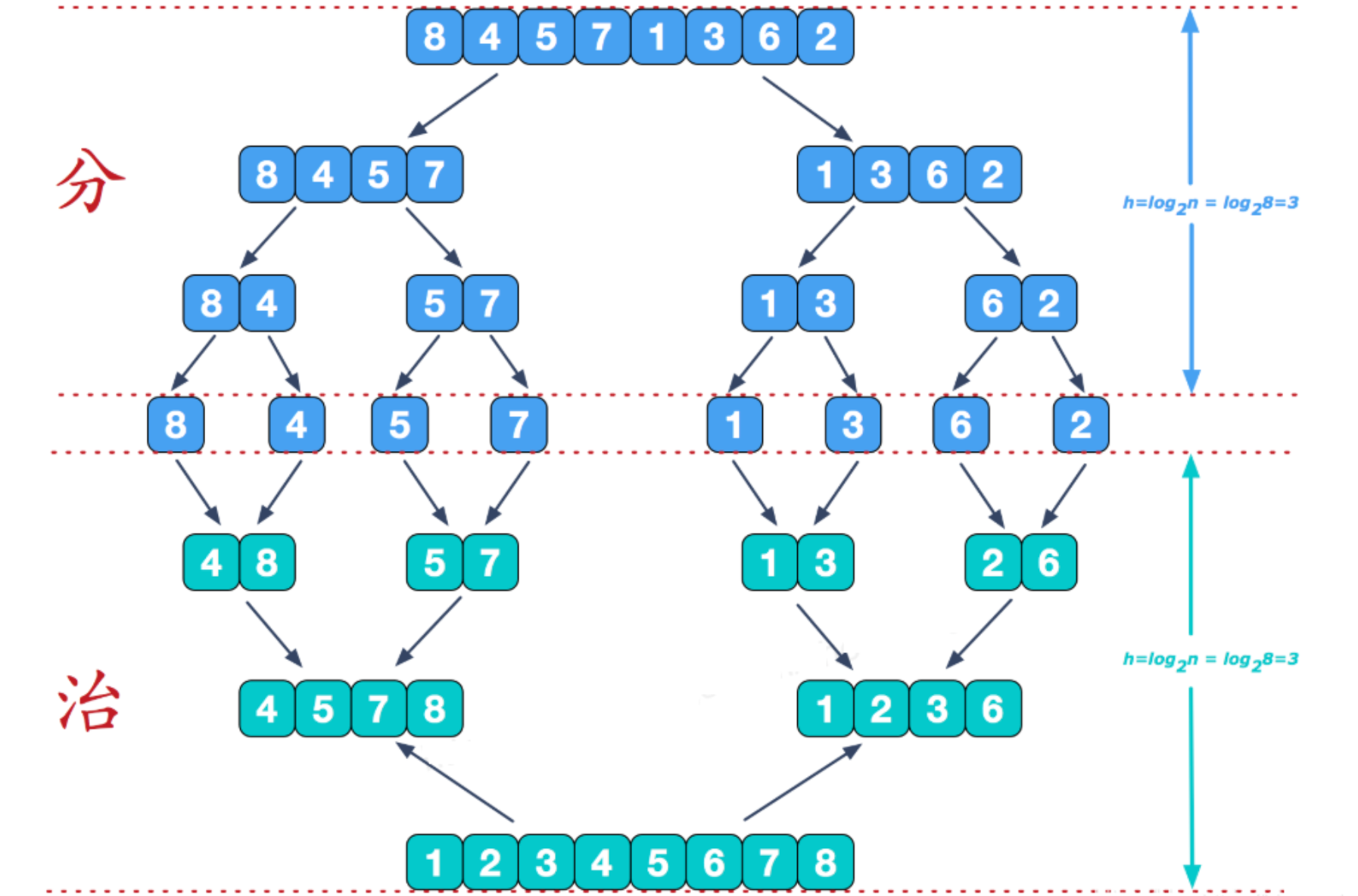
归并排序:
归并排序(Merge Sort)是基于分治思想的经典排序算法,核心逻辑是 "分而治之" ,把复杂排序问题拆分成简单子问题解决,再合并结果
算法步骤:
分解阶段:
- 将当前待排序数组从中间位置分为两部分
- 计算中点: mid = left + (right - left) / 2
- 递归地对左右两部分继续分解,直到子数组长度为1
解决阶段:
- 当前子数组长度为1时,说明该子数组是有序的
- 开始从最底层向上回朔
合并阶段:
- 将两个已排序的子数组合并为一个有序数组
- 使用双指针法比较两个子数组的元素
- 较小的元素放入临时数组
动图演示:
性能分析:
时间复杂度:
- 不管数组初始是否有序,时间复杂度都是O(nlogn) 【拆分"过程是对数级(每次规模减半,拆分次数为log2n),"合并"是线性级(每次合并遍历n个元素)】
空间复杂度:
- 因合并需要额外临时数组存数据,空间复杂度O(n) n为元素个数
稳定性:
- 稳定排序
代码实现(Java):
java
public class MergeSort {
/**
* 归并排序主方法
* @param arr 待排序数组
* @param left 当前子数组的起始索引
* @param right 当前子数组的结束索引
*/
public static void mergeSort(int[] arr, int left, int right) {
// 递归终止条件:当子数组只有一个元素时(left == right)
if (left >= right) {
return;
}
// 计算中间点(注意防止整数溢出)
int mid = left + (right - left) / 2;
// 递归排序左半部分
mergeSort(arr, left, mid);
// 递归排序右半部分
mergeSort(arr, mid + 1, right);
// 合并两个已排序的子数组
merge(arr, left, mid, right);
}
/**
* 合并两个有序子数组
* @param arr 原始数组
* @param left 左子数组起始索引
* @param mid 分割点(左子数组结束索引)
* @param right 右子数组结束索引
*/
public static void merge(int[] arr, int left, int mid, int right) {
// 创建临时数组存储合并结果
int[] temp = new int[right - left + 1];
// 初始化指针:i-左子数组,j-右子数组,k-临时数组
int i = left, j = mid + 1, k = 0;
// 比较两个子数组的元素,较小的先放入temp
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++]; // 稳定排序的关键:相等时取左边元素
} else {
temp[k++] = arr[j++];
}
}
// 将左子数组剩余元素复制到temp
while (i <= mid) {
temp[k++] = arr[i++];
}
// 将右子数组剩余元素复制到temp
while (j <= right) {
temp[k++] = arr[j++];
}
// 将排序好的temp数组复制回原数组
for (int p = 0; p < temp.length; p++) {
arr[left + p] = temp[p];
}
}
public static void main(String[] args) {
int[] arr = {5, 2, 8, 3, 6, 1, 7, 9, 4};
System.out.println("排序前: " + Arrays.toString(arr));
mergeSort(arr, 0, arr.length - 1);
System.out.println("排序后: " + Arrays.toString(arr));
}
}