非线性激活

一、 非线性激活是什么

想象一个神经网络里的神经元（Neuron）。它会接收来自上一层多个神经元的输入信号。这些信号被加权求和后，得到一个总的输入值。

激活函数的作用，就像是这个神经元的"审批开关"或"情绪调节器"。

它接收这个总输入值，然后决定：

• 是否要激活？ (要不要把信息传递下去)
• 要传递多强的信息？ (传递原始信息，还是打个折，或者增强一下)

非线性激活函数就是一个"有个性的"审批开关。它不是简单地把输入值原封不动地传出去（那是线性激活），而是会根据输入值的大小，进行一次非线性的"加工"或"扭曲"，然后再输出。

二、为什么必须用非线性激活函数？

这是最核心的问题。一句话概括：如果没有非线性激活函数，再深的神经网络也只相当于一个单层网络。

假设我们不用任何激活函数，或者用一个线性的激活函数（比如 f(x) = ax）。

• 一个单层网络可以表示为：output = W1 * input + b1
• 一个两层网络可以表示为：h1 = W1 * input + b1，output = W2 * h1 + b2

把 h1 代入第二个式子，得到： output = W2 * (W1 * input + b1) + b2 output = (W2 * W1) * input + (W2 * b1 + b2)

令 W = W2 * W1，b = W2 * b1 + b2，你会发现，这个两层网络最终还是可以写成 output = W * input + b 的形式。

结论就是： 无论叠加多少个线性层，其最终效果都等同于一个单独的线性层。这样的网络只能学习线性关系，比如线性回归。但现实世界中的绝大多数问题，比如图像识别、语音识别，都是高度非线性的。

非线性激活函数的作用就是"掰弯"这个线性关系。 它在每一层都引入了非线性变换，使得神经网络的层数有了意义，每一层都可以学习到输入数据中不同层次、不同抽象维度的特征。这使得深层网络能够拟合极其复杂的函数，从而获得强大的表达能力。

三、 常见的非线性激活函数

a. Sigmoid (S型函数)

• 公式 : f(x) = 1 / (1 + e^(-x))

• 图像: 一条平滑的S形曲线。

• 输出范围: (0, 1)

• 优点:

  • 输出值在0到1之间，可以被解释为"概率"，非常适合用在二分类问题的输出层。
  • 函数平滑，处处可导。

• 缺点 (致命的) :

  1. 梯度消失 (Vanishing Gradients) : 当输入 x 的绝对值非常大时（比如大于5或小于-5），Sigmoid函数的导数（梯度）趋近于0。在反向传播时，梯度需要逐层相乘，如果多层都使用Sigmoid，梯度会迅速衰减为0，导致网络底层部分的权重无法更新，模型学不到东西。这是它在深层网络中被弃用的主要原因。
  2. 输出非零中心 (Not Zero-centered) : 输出恒为正数。这会导致在反向传播时，对权重的梯度更新方向总是同为正或同为负，使得梯度下降的收敛过程变慢（呈"Z"字形下降）。
  3. 计算成本高 : 指数运算（e^x）比简单的加减乘除要耗时。

b. Tanh (双曲正切函数)

• 公式 : f(x) = (e^x - e^(-x)) / (e^x + e^(-x))

• 图像: 和Sigmoid类似，但更陡峭。

• 输出范围: (-1, 1)

• 优点:

  • 输出是零中心的: 相比Sigmoid，它的输出均值为0，解决了"非零中心"问题，收敛速度更快。

• 缺点:

  • 仍然存在梯度消失问题: 当输入绝对值很大时，梯度同样趋近于0。
  • 计算成本高: 同样有指数运算。

c. ReLU (Rectified Linear Unit / 修正线性单元)

这是目前在深层网络中最受欢迎、最常用的激活函数。

• 公式 : f(x) = max(0, x)

• 图像: 一条"折线"，输入为负时输出为0，输入为正时原样输出。

• 输出范围: [0, +∞)

• 优点:

  1. 解决了梯度消失问题 (在正区间) : 当输入为正时，导数恒为1，梯度可以无损地在网络中传播，使得训练深层网络成为可能。
  2. 计算速度极快: 只需一个简单的判断和赋值操作，没有复杂的指数运算。
  3. 稀疏性 (Sparsity) : 它会使一部分神经元的输出为0，这意味着网络可以变得"稀疏"，减少了参数间的依赖，可能有助于防止过拟合。

• 缺点:

  1. Dying ReLU Problem (神经元死亡问题) : 如果一个神经元的输入在训练过程中恒为负，那么它的输出将永远是0，梯度也永远是0。这个神经元的权重将永远不会被更新，它就"死亡"了。
  2. 输出非零中心: 和Sigmoid一样。

d. Leaky ReLU / PReLU

为了解决"Dying ReLU"问题而诞生。

• Leaky ReLU 公式 : f(x) = max(αx, x)，其中 α 是一个很小的常数，如0.01。

• PReLU 公式 : 和Leaky ReLU一样，但 α 不是固定的，而是作为一个参数参与网络训练。

• 图像: 和ReLU类似，但在负区有一条微小的、不为零的斜率。

• 优点:

  • 解决了"Dying ReLU"问题，因为负输入的梯度不再是0，而是 α。
  • 保留了ReLU的大部分优点，如计算高效、收敛快。

• 缺点:

  • 在实践中，其性能提升不总是很明显。

e. ELU (Exponential Linear Unit)

• 公式 : f(x) = x if x > 0, and α(e^x - 1) if x <= 0。

• 优点:

  • 兼具ReLU和Leaky ReLU的优点。
  • 输出的均值更接近0（相比ReLU），具有更好的收敛特性。
  • 在负区间是"软饱和"，可以对噪声有更强的鲁棒性。

• 缺点:

  • 计算量比ReLU大，因为有指数运算。

f. GELU (Gaussian Error Linear Unit) / Swish

这些是近年来在SOTA（State-of-the-art）模型（如BERT, GPT）中流行的激活函数。

• GELU : x * Φ(x)，其中 Φ(x) 是高斯分布的累积分布函数。可以看作是根据输入值的分布来对其进行随机正则化的一种形式。
• Swish : x * sigmoid(βx)。β 是一个可学习的参数。

它们都是平滑、非单调的函数，在很多任务上的表现都优于ReLU，但计算也更复杂。

四、如何选择？

1. 首选 ReLU: 它是绝大多数情况下的默认选择。如果你不确定用什么，就先用ReLU。它速度快，性能通常也很好。

2. 观察神经元死亡情况 : 如果你在训练中发现有大量的神经元输出持续为0（可以通过可视化工具查看），可以尝试 Leaky ReLU 或 PReLU，看看是否能改善性能。

3. 追求极致性能 : 如果计算资源不是瓶颈，并且你希望压榨出模型的最后一点性能，可以尝试 ELU , GELU , 或 Swish。尤其是在Transformer架构中，GELU和Swish非常常见。

4. Sigmoid 和 Tanh 的使用场景:

   • 隐藏层 : 在深度神经网络中，尽量避免在隐藏层使用Sigmoid和Tanh，因为它们的梯度消失问题太严重。

   • 输出层: 它们在输出层仍然非常有用。

     • Sigmoid: 用于二分类问题的输出层（输出概率）。
     • Tanh: 用于输出值范围在 [-1, 1] 之间的回归问题，或某些模型的中间状态（如RNN）。

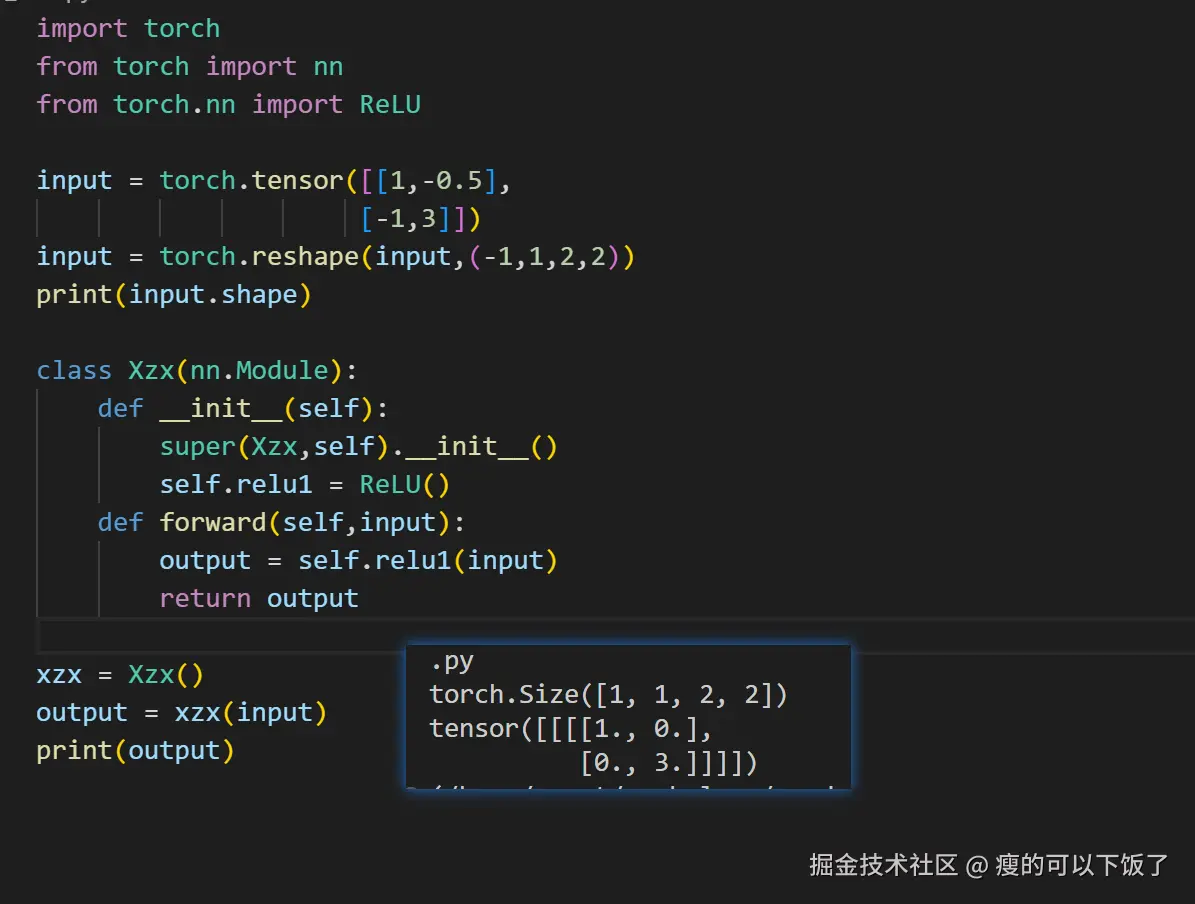
五、实操（实现一个简单的ReLU）