二分查找算法，并分析其时间、空间复杂度

查找算法中的"二分法"是这样定义的:

给定N个从小到大排好序的整数序列List，以及某待查找整数X，我们的目标是找到X在List中的下标。即若有List=X，则返回i;否则返回-1表示没有找到。

二分法是先找到序列的中点List $M$ ，与X进行比较，若相等则返回中点下标:否则，若list $M$ >X、则在左边的子系列中査找X:若list $M$ <X、则在右边的子系列中査找X。

我最开始是这样写的

java 复制代码

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
var search = function(nums, target) {
    let left = 0 
    let right = nums.length - 1;
    let center = (left + right)/2
    while (left <= right){
        if(nums[center]>target){
            right = center
        }
        else if(nums[center] == target){
            return center
        }
        else{
            left = center
        }
    }
    return -1 
};

提交结果为

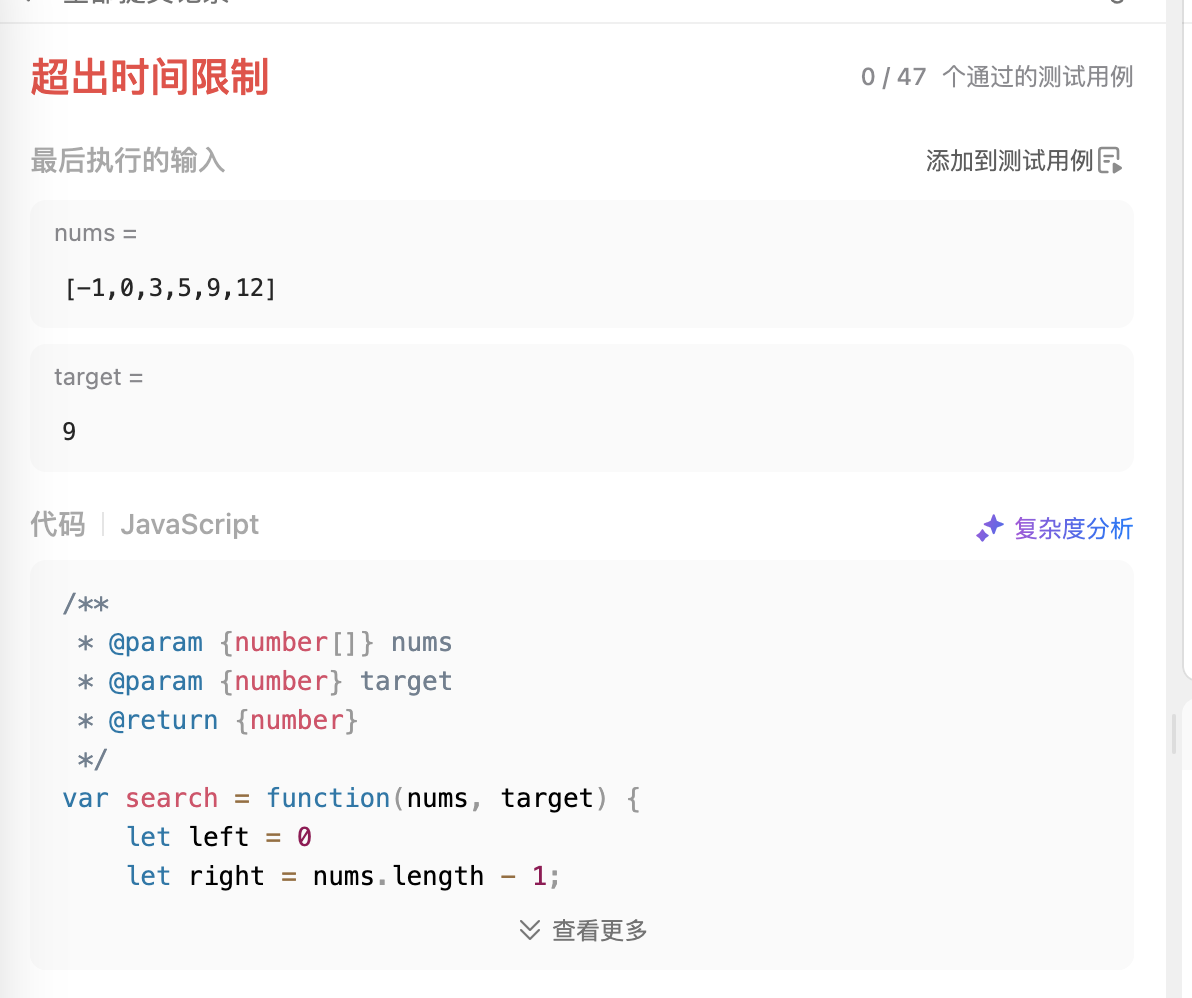
错误原因在于 let center = (left + right)/2应该写在while函数里面。按照我上面的错误代码一直执行 left = center了。

更改代码

java 复制代码

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
var search = function(nums, target) {
    let left = 0 
    let right = nums.length - 1;
    while (left <= right){
       let center = (left + right)/2
        if(nums[center]>target){
            right = center
        }
        else if(nums[center] == target){
            return center
        }
        else{
            left = center
        }
    }
    return -1 

};

提交结果于上述一样问了豆包

错误原因有二

首先 (left + right)/2 可能产生小数（例如当 left=2, right=3 时得到 2.5），而数组索引必须是整数，导致访问错误位置的元素
其次直接将 right 或 left 设置为 center，而没有 +1 或 -1，这可能陷入无限循环（例如 nums = $1, 3$ ,targat =2 这样left永远为1，right永远为2）。

新的代码

java 复制代码

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
var search = function(nums, target) {
    let left = 0 
    let right = nums.length - 1;
    while (left <= right){
       let center = Math.floor(left + right)/2
        if(nums[center]>target){
            right = center - 1
        }
        else if(nums[center] == target){
            return center
        }
        else{
            left = center + 1
        }
    }
    return -1 

};

依旧报错

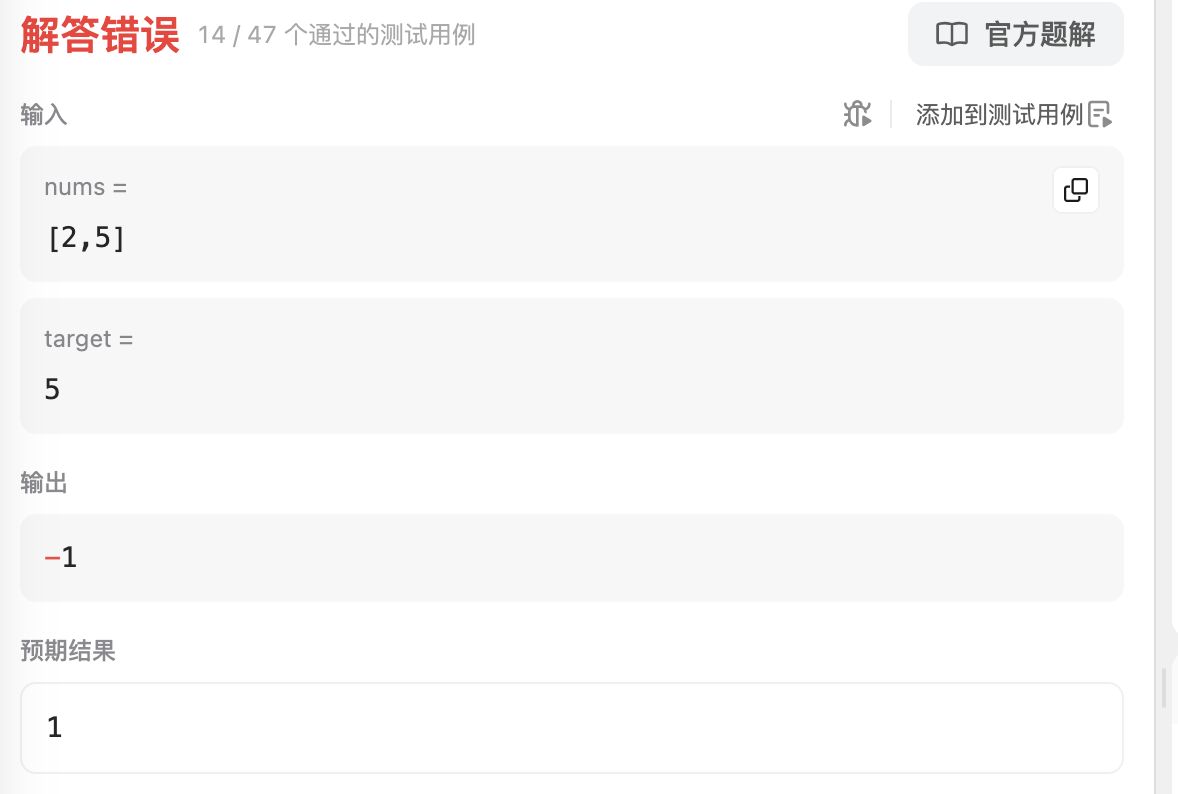
错误原因

正确的中间索引计算应该是先计算 left + right 的和，再除以 2，最后进行取整。而我的代码是先对 left + right 取整，再除以 2，这会导致计算结果错误。将 let center = Math.floor(left + right)/2 改为 let center = Math.floor((left + right)/2)

正确的代码为

java 复制代码

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
var search = function(nums, target) {
    let left = 0 
    let right = nums.length - 1;
    while (left <= right){
       let center = Math.floor((left + right)/2)
        if(nums[center]>target){
            right = center - 1
        }
        else if(nums[center] == target){
            return center
        }
        else{
            left = center + 1
        }
    }
    return -1 

};

分析时间空间复杂度

时间复杂度

最好情况：目标值刚好是序列中点，只需查找 1 次就能找到，时间复杂度为 O(1)。
最坏情况：每次查找都缩小一半范围，直到只剩 1 个元素才确定结果。时间复杂度为O(logn)。

空间复杂度

不管序列多长，算法运行过程中仅用到固定几个额外变量（left、right、mid 等），所以空间复杂度为

O(1)。

做完题感触

曾经很会的题，今天花了好久才作出来。退步了好多。