此练习,主要是使用状态空间方程来设计控制器的方法和思路:
①系统建模;
②系统的能控性;
③极点配置;
④最优化控制LQR;
⑤轨迹追踪;
以下是,第②部分:系统的能控性;
一、判断系统能控性
- 状态能控定义:对于系统而言,如果存在着输入u(t),可以在有限的时间区间[t0,t1]内,将系统的状态变量从初始状态z(t0)转移到终端状态z(t1),那么就称状态z(t0)是能控的状态。如果在任意的初始时间t0下的初始状态z(t0)都能控,就称系统的状态是能控的。
- 需要指出,如果系统的状态z(t)能控,系统的输出y(t)也一定能控。
- 在设计状态反馈控制器,之前需要先判断,系统是否是能控的;判断系统是否能控,就需要判断能控矩阵Co,其矩阵形式如下;
- 对于n维线性时不变系统而言,它的状态能控的充分必要条件是能控矩阵的秩为n。
- 判断此时矩阵Co的秩是否为n,秩为n,则系统可控;
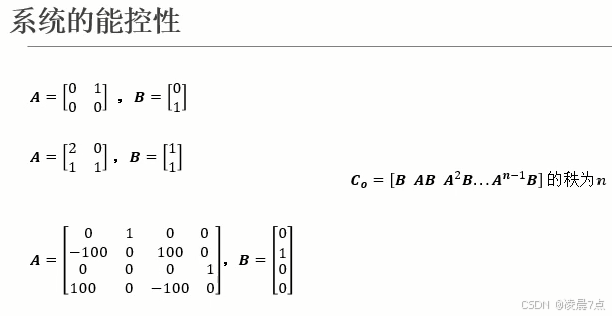
- 以其中第三个例子,在MATLAB算出:
matlab
clc;clear;close all;
%% 定义矩阵A,B
A =[[ 0 1 0 0 ];
[ -100 0 100 0];
[0 0 0 1];
[100 0 -10 0]
];
B=[0;1;0;0];
Co=ctrb(A,B); % ctrb,可以直接求出能控矩阵Co
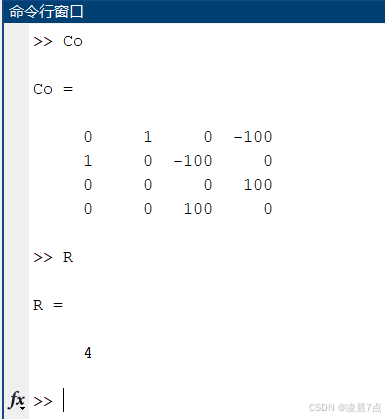
R = rank(Co) ; % rank,求秩- 运行结果:
- 在命令行窗口,分别输入Co和R;
- 可以看出,秩为R=4,所以说明系统是可控系统;
- 此例子三数学模型,对应的系统如下图;
- 两个小车通过弹环连接,右边有一外力;
- 因为上面分析这是可控的,所以可以通过控制外力,来控制里面每一个状态变量的值。
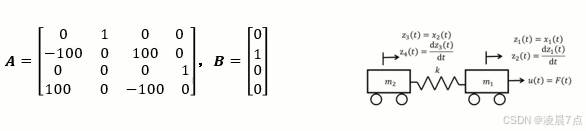
学习来源:《控制之美》[卷1],王天威