强化学习笔记：从Q学习到GRPO

推荐学习huggingface的强化学习课程，全面了解强化学习的发展史。

以下是个人笔记，内容不一定完整，有些是个人理解。

基于值函数(value function)的强化学习

• 基于值函数(value function)的强化学习：学习的是一个值函数，即Q函数，其能够给出当前state下每个action的Q值。在部署时，可以选择贪婪策略，那么每个state都会选择Q值最大的action，因此策略属于固定策略（state确定时，只有唯一确定的action）；或使用随机策略，Q值越大被选择概率越大。
  在这种情况下，重点是学习出一个Q函数，而policy本身是预定义的简单规则（不是神经网络）。

Q与V的定义

V(s): 状态价值函数，表示从这个状态开始，直到最终状态，预期得到的反馈的总和

Q(a,s)：动作价值函数，表示从这个状态开始并采取这个action，预期得到的反馈的总和

两者可以互相计算，V就是这个state下所有action在策略下的期望

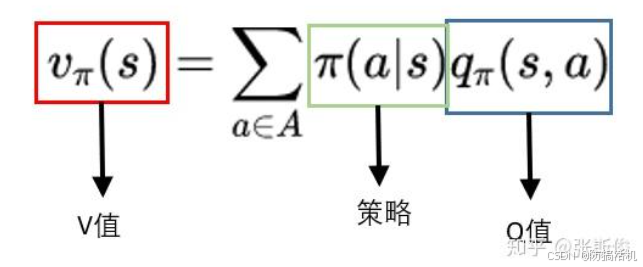
因此，如果选取的是贪婪策略，则 V ( s t + 1 ) = max ⁡ a Q ( s t + 1 , a ) V(s_{t+1})=\max_aQ(s_{t+1},a) V(st+1)=maxaQ(st+1,a)，即Q值最大的action的Q值。这在Q学习中将会用到

而 Q ( s t , a ) = r + γ V ( s t + 1 ) Q(s_t,a)=r+\gamma V(s_{t+1}) Q(st,a)=r+γV(st+1)，即在 s t s_t st采取了a后，获得了反馈r并进入了 s t + 1 s_{t+1} st+1

更新V

由于理论上计算V(s)需要从s开始遍历之后所有路径，非常麻烦，因此提出了贝尔曼公式，使用 V ( s t + 1 ) V(s_{t+1}) V(st+1) 来计算 V ( s t ) V(s_t) V(st)

更新V有2种方法，蒙特卡洛法和时间差分法。

蒙特卡洛法：从S_t开始，走到最终状态，计算轨迹上累积的反馈，以此更新 V ( s t ) V(s_t) V(st)

时间差分法：从S_t开始，只需要走一步，获取 R t + 1 R_{t+1} Rt+1和 S t + 1 S_{t+1} St+1，使用 R t R_t Rt 和 V ( s t + 1 ) V(s_{t+1}) V(st+1) 来更新 V ( s t ) V(s_t) V(st)。这符合bellman 公式。由于未来的价值与现在的价值不一定等价，我们需要更加考虑现在，因此会给未来的价值一个折扣率，例如 γ = 0.9 \gamma=0.9 γ=0.9

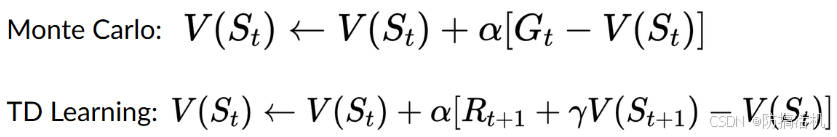
Q学习

著名的Q学习就是使用 TD learning 来更新Q表，给每个 state-action 对 更新Q值。与环境交互的策略通常是ε-greedy，即ε概率纯随机选取action，1-ε概率选取贪婪action。

使用TD learning+贪婪策略来更新Q值，公式如下
Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + Q ( S t + 1 , A t + 1 ) − Q ( S t , A t ) ] Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha[R_{t+1}+Q(S_{t+1},A_{t+1})-Q(S_t,A_t)] Q(St,At)←Q(St,At)+α[Rt+1+Q(St+1,At+1)−Q(St,At)]

贪婪策略下，A_{t+1}根据最大q值来选取，因此可以写为：
Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ m a x a Q ( S t + 1 , a ) − Q ( S t , A t ) ] Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha[R_{t+1}+\gamma max_aQ(S_{t+1},a)-Q(S_t,A_t)] Q(St,At)←Q(St,At)+α[Rt+1+γmaxaQ(St+1,a)−Q(St,At)]

因为我们实际运行使用ε-greedy，而更新Q值却使用贪婪策略，这两个策略不一样，因此Q学习属于 off-policy

Sarsa是Q学习的变体，属于on-policy，其在更新Q值时会使用ε-greedy选取action A 来计算 Q ( S t + 1 , A ) Q(S_{t+1},A) Q(St+1,A)，因此属于 on-policy

深度Q学习

由于更复杂的游戏中，state的数量无法完全列出，我们只能把当前游戏截图作为state（通常是连续的多帧截图，这样才能反映物品的运动方向），输入给神经网络θ，神经网络给出每个action的Q值。

于是，我们将 Q-Loss = Q-target − Q θ ( S t , A t ) = R t + 1 + γ m a x a Q ( S t + 1 , a ) − Q θ ( S t , A t ) \text{Q-Loss}=\text{Q-target}-Q_\theta(S_t,A_t)=R_{t+1}+\gamma max_aQ(S_{t+1},a)-Q_\theta(S_t,A_t) Q-Loss=Q-target−Qθ(St,At)=Rt+1+γmaxaQ(St+1,a)−Qθ(St,At)作为loss，利用梯度去更新神经网络

传统Q学习，做一步，学习一次，然后就丢弃这部分数据。为了提高对经验的利用率，deep-Q学习使用了"经验回放"来利用以前的数据：每次得到的 （ s t , a t , r t , s t + 1 ） （s_t,a_t,r_t,s_{t+1}） （st,at,rt,st+1）（St,a,r,St+1）会被存入经验池（容量为N）。学习时，从经验池中随机抽取一些数据来更新网络。

然而，由于Q-target和当前Q值都是用同一个神经网络计算出的，所以一旦更新这个网络，那么target也在变化，这导致训练震荡（永远跟不上target的变化）。所以，我们将计算Q-target所用的参数θ固定起来记为 θ − \theta^- θ−，每经过C步才会更新它为 θ \theta θ

Double DQN: 由于一开始Q值都是0，所以我们不知道下一状态的最优动作是什么，选取最大Q值动作会带来很大噪声，例如，错误的给一个非最优动作一直分配很大Q值，进入恶性循环。因此我们用两个不同网络，将action选取与Q值计算解耦：用 DQN network 来选择 下一状态的动作，即 m a x a Q ( S t + 1 , a ) max_aQ(S_{t+1},a) maxaQ(St+1,a)中的a，但是用target network来计算下一状态的动作的Q值。

基于策略的强化学习：学习的是策略 ，不需要学习value function（和policy融合了）

策略梯度法

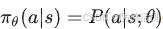
策略具有参数 θ，给定state，每个action有不同概率被选取

相比于基于value function的方法，策略梯度法具有以下优点：

1. 策略具有随机性，而不是贪婪策略，避免被卡在循环里，不需要人为平衡 探索-利用
2. 连续动作空间下，传统value function下只能给出Q值，我们不知道如何选取最优动作 。而策略梯度法的策略，可以给出整个动作空间的概率分布。
3. 传统Q学习使用了max，可能会导致Q函数更新后，max的action立刻变为另一个，导致不稳定；而策略梯度法变化更平滑

缺点：

1. 训练更慢
2. 经常陷入局部最优
3. 高方差，即同个环境下，训出来的策略也很不一样

通常，我们让agent在一个episode中不断与环境交互直至结束，如果最后赢了，那么所有动作都会被视为好

强化学习是基于反馈假设的：所有目标都可以被描述为将期望累积反馈最大化。由此，我们优化是目标是使整条动作轨迹τ的总的反馈最大，因此目标函数如下：

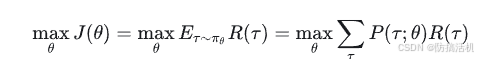
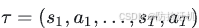
可以解释为，最大化-所有不同轨迹求和-每个轨迹的总反馈*策略θ下这个轨迹发生的概率

轨迹在策略π下发生的概率是：每个t时刻，采取 a t a_t at的概率 乘以 采取 a t a_t at后转移到 s t + 1 s_{t+1} st+1 的概率

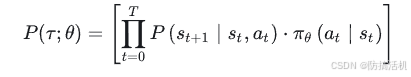
为了优化这个函数，我们需要计算 J 对于 θ 的导数，从而使用梯度法逐步优化 θ：

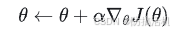
计算导数推导过程如下，主要使用了 log 求导技巧，即 ∇ x l o g f ( x ) = ∇ x f ( x ) f ( x ) \nabla_xlogf(x)=\frac{\nabla_xf(x)}{f(x)} ∇xlogf(x)=f(x)∇xf(x)

于是我们可以化简导数：
∇ θ J ( θ ) = ∑ τ ∇ θ P ( τ ; θ ) R ( τ ) = ∑ τ P ( τ ; θ ) P ( τ ; θ ) ∇ θ P ( τ ; θ ) R ( τ ) = ∑ τ P ( τ ; θ ) ∇ θ l o g P ( τ ; θ ) R ( τ ) \nabla_\theta J(\theta)=\sum_\tau\nabla_\theta P(\tau;\theta)R(\tau)=\sum_\tau \frac{P(\tau;\theta)}{P(\tau;\theta)}\nabla_\theta P(\tau;\theta)R(\tau) \\ =\sum_\tau P(\tau;\theta) \nabla_\theta log P(\tau;\theta)R(\tau) ∇θJ(θ)=τ∑∇θP(τ;θ)R(τ)=τ∑P(τ;θ)P(τ;θ)∇θP(τ;θ)R(τ)=τ∑P(τ;θ)∇θlogP(τ;θ)R(τ)

因为 ∇ θ l o g P ( τ ( i ) ; θ ) = ∇ θ l o g μ ( s 0 ) + ∇ θ ∑ t = 0 H l o g P ( s t + 1 ( i ) ∣ s t ( i ) a t ( i ) ) + ∇ θ ∑ t = 0 H l o g π θ ( a t ( i ) ∣ s t ( i ) ) = ∇ θ ∑ t = 0 H l o g π θ ( a t ( i ) ∣ s t ( i ) ) \nabla_\theta logP(\tau^{(i)};\theta)=\nabla_\theta log\mu(s_0)+\nabla_\theta\sum_{t=0}^HlogP(s_{t+1}^{(i)}|s_t^{(i)}a_t^{(i)})+\nabla_\theta\sum_{t=0}^Hlog\pi_\theta(a_t^{(i)}|s_t^{(i)})=\nabla_\theta\sum_{t=0}^Hlog\pi_\theta(a_t^{(i)}|s_t^{(i)}) ∇θlogP(τ(i);θ)=∇θlogμ(s0)+∇θt=0∑HlogP(st+1(i)∣st(i)at(i))+∇θt=0∑Hlogπθ(at(i)∣st(i))=∇θt=0∑Hlogπθ(at(i)∣st(i))

从而导数化简为
∇ θ J ( θ ) = ∑ τ P ( τ ; θ ) ∑ t = 0 H ∇ θ l o g π θ ( a t ( i ) ∣ s t ( i ) ) R ( τ ) \nabla_\theta J(\theta) =\sum_\tau P(\tau;\theta) \sum_{t=0}^H\nabla_\theta log\pi_\theta(a_t^{(i)}|s_t^{(i)})R(\tau) ∇θJ(θ)=τ∑P(τ;θ)t=0∑H∇θlogπθ(at(i)∣st(i))R(τ)

现实中，我们不可能遍历所有情况，所以我们通过m次采样获得m条轨迹，从而近似此导数为：
∇ θ J ( θ ) ≈ 1 n ∑ i = 1 n ( R ( τ ( i ) ) ∑ t = 0 T ∇ θ log ⁡ π θ ( a t ( i ) ∣ s t ( i ) ) ) \nabla_\theta J(\theta) \approx\frac{1}{n}\sum_{i=1}^{n}(R(\tau^{(i)}) \sum_{t=0}^T\nabla_{\theta}\log\pi_{\theta}(a_{t^{(i)}}\mid s_{t^{(i)}})) ∇θJ(θ)≈n1i=1∑n(R(τ(i))t=0∑T∇θlogπθ(at(i)∣st(i)))
R ( τ i ) R(\tau^i) R(τi)表示从0到T时刻这条轨迹累积的反馈，n表示样本个数（轨迹条数）

利用此公式，即可优化θ

Actor-critic

策略梯度法的方差大，因为我们需要使用蒙特卡洛法进行采样，即使初始状态一样，后续产生的采样轨迹也很不同，从而带来方差。如果想要方差小，那就要非常多的样本数量，但这样又导致训练缓慢。但好处是，这种方法直接使用真实反馈（而不是估计的反馈）来计算总反馈，因此是无偏见的。

Actor-critic结合了value-based和policy-based方法，使用了两个模块：

actor (θ)：控制了agent的行动，使用policy-based

critic (ω)：评价动作的好坏，使用value-based

Critic 相当于一个从环境中学习到的 value function，可以给出动作的Q值。这样更稳定，每一步都有Q值，而策略梯度法很多时候只有最后的状态才有反馈。

工作流程是：

1. 从s_t开始，actor选择动作a_t，与环境交互，获得 s t + 1 , r t + 1 s_{t+1}, r_{t+1} st+1,rt+1
2. Critic 评价动作，获得 Q值 q w ( s t , a t ) q_w(s_t,a_t) qw(st,at)
3. actor使用Q值更新自身参数 Δ θ = α ∇ θ ( l o g π θ ( s , a ) ) q ^ w ( s , a ) \Delta\theta=\alpha\nabla_\theta(log\pi_\theta(s,a))\hat{q}w(s,a) Δθ=α∇θ(logπθ(s,a))q^w(s,a) ，然后再使用更新的参数选择动作a{t+1}
4. Critic 使用 TD error 来更新自身参数（类似于DQN）

为了进一步稳定训练，我们引入了优势函数 A ( s , a ) = Q ( s , a ) − V ( s ) A(s,a)=Q(s,a)-V(s) A(s,a)=Q(s,a)−V(s) 其代表了这个动作的相对优势，即采取这个动作后，相比于平均反馈，我们能额外获得多少反馈。用优势函数去代替actor更新公式里的Q值，可以使反馈有正有负，使训练更稳定。

但是这样子需要有2个critic分别估计Q和V，很麻烦，因此我们只保留估计V的critic网络（也可以视为是优势函数的估计网络），用V去估计Q： Q ( s t , a ) = r + γ V ( s t + 1 ) Q(s_t,a)=r+\gamma V(s_{t+1}) Q(st,a)=r+γV(st+1)，从而actor更新公式变为：
Δ θ = α ∇ θ ( l o g π θ ( s , a ) ) A ( s , a ) = α ∇ θ ( l o g π θ ( s , a ) ) ( r + γ V ( s t + 1 ) − V ( s t ) \Delta\theta=\alpha\nabla_\theta(log\pi_\theta(s,a))A(s,a)=\alpha\nabla_\theta(log\pi_\theta(s,a))(r+\gamma V(s_{t+1})-V(s_t) Δθ=α∇θ(logπθ(s,a))A(s,a)=α∇θ(logπθ(s,a))(r+γV(st+1)−V(st)

PPO

传统策略梯度法容易导致参数更新太大或太小，因此TRPO等方法引入了KL散度惩罚项，防止更新太大。

PPO-penalty 和TRPO类似，也使用了KL散度惩罚项，但其惩罚力度是动态的，如果上一步更新过大，则加大惩罚系数，反之减小。

现在常用的PPO是PPO-clip，其在目标函数里面直接对更新的幅度进行限制。

描述更新策略相对于原策略的预期优势称为替代优势（surrogate advantage）

A 称为优势函数，衡量了一个动作的相对优势，A大于0，代表这个动作相对于其它动作有优势。
J ( π θ + Δ θ ) − J ( π θ ) ≈ E s ∼ ρ π θ π θ + Δ θ ( a ∣ s ) π θ ( a ∣ s ) A π θ ( s , a ) = L π θ ( π θ + Δ θ ) J(\pi_{\theta+\Delta\theta})-J(\pi_\theta)\approx\mathbb{E}{s\sim\rho{\pi\theta}}\frac{\pi_{\theta+\Delta\theta}(a\mid s)}{\pi_\theta(a\mid s)}A^{\pi_\theta}(s,a)=\mathcal{L}{\pi\theta}(\pi_{\theta+\Delta\theta}) J(πθ+Δθ)−J(πθ)≈Es∼ρπθπθ(a∣s)πθ+Δθ(a∣s)Aπθ(s,a)=Lπθ(πθ+Δθ)

为了直接对更新幅度进行限制，PPO将原本的目标函数里的 log \\pi_\\theta(a_t\|s_t) 替换为相对选取这个action的概率，所以PPO 的目标函数如下：
L C L I P ( θ ) = E t [ min ⁡ ( r t ( θ ) A t , clip ⁡ ( r t ( θ ) , 1 − ϵ , 1 + ϵ ) A t ) ] L^{CLIP}(\theta)=\mathbb{E}_t\left[\min\left(r_t(\theta)A_t,\operatorname{clip}(r_t(\theta),1-\epsilon,1+\epsilon)A_t\right)\right] LCLIP(θ)=Et[min(rt(θ)At,clip(rt(θ),1−ϵ,1+ϵ)At)]

其中：

r_t(\\theta) 是概率比率， 是概率比率， 是概率比率，r_t(\\theta)=\\frac{\\pi_\\theta(a_t\|s_t)}{\\pi_{\\theta_\\mathrm{old}}(a_t\|s_t)}它表示新策略和旧策略在同一状态下选择动作的概率比值。注意 θ o l d \theta_{old} θold是永远固定的，因此是定值，对θ导数为0。

剪辑操作 clip ⁡ ( r t ( θ ) , 1 − ϵ , 1 + ϵ ) :将 r t ( θ ) 限制在区间 [ 1 − ϵ , 1 + ϵ ] 内，防止策略变化过大。 \operatorname{clip}(r_t(\theta),1-\epsilon,1+\epsilon)\text{:将}r_t(\theta)\text{限制在区间}[1-\epsilon,1+\epsilon]_\text{内，防止策略变化过大。} clip(rt(θ),1−ϵ,1+ϵ):将rt(θ)限制在区间[1−ϵ,1+ϵ]内，防止策略变化过大。

ϵ \epsilon ϵ通常选0.2

在优势函数分别为正和负时，clip的功能不一样：

1. 优势函数为正时，此时如果我们的策略选取a的概率本来就已经很高（r超过了 1 + ϵ 1+\epsilon 1+ϵ），我们不想太贪婪地继续增加其概率，会将其限制在不超过 1 + ϵ 1+\epsilon 1+ϵ，此时目标函数对 θ \theta θ的导数为0，即不再继续更新网络增加a的概率
2. 优势函数为负时，此时如果我们的策略选取a的概率本来就已经很低（r低于 1 − ϵ 1-\epsilon 1−ϵ），我们不想太贪婪地继续减小其概率，会将其限制在不低于 1 − ϵ 1-\epsilon 1−ϵ，此时目标函数对 θ \theta θ的导数也为0
3. 其余情况，相当于未被clip，正常求导，和actor-critic一样
   如果只有clip项，会导致在需要快速更新参数的情况下，即a概率低但A为正的情况下（或a概率高在A为负）导数也为0，导致收敛太慢或无法收敛。

PPO实际训练llm时的操作

1. 实际在训练llm时，reward model 会输入整个序列，然后给每个token输出一个分数，作为 r t r_t rt。value model 同样也是输入整个序列，给每个token输出一个分数，作为 V ( s t ) V(s_t) V(st)，再使用 A t = r t + 1 + γ V ( s t + 1 ) − V ( s t ) A_t=r_{t+1}+\gamma V(s_{t+1})-V(s_t) At=rt+1+γV(st+1)−V(st)计算出优势函数
2. 实际训练时，将目标函数加一个负号，就变成损失函数。
3. 求 π θ ( a t ∣ s t ) \pi_\theta(a_t|s_t) πθ(at∣st)即每个token的概率时，得到 logits 后，会使用 log_softmax（比softmax更快）得到 log_prob，然后计算 r t ( θ ) r_t(\theta) rt(θ)时，再加一个exp，即 r t ( θ ) = π θ ( a t ∣ s t ) π θ o l d ( a t ∣ s t ) = e x p ( l o g π θ ( a t ∣ s t ) − l o g π θ o l d ( a t ∣ s t ) ) r_t(\theta)=\frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_\mathrm{old}}(a_t|s_t)}=exp(log \pi_\theta(a_t|s_t) - log \pi_{\theta_\mathrm{old}}(a_t|s_t)) rt(θ)=πθold(at∣st)πθ(at∣st)=exp(logπθ(at∣st)−logπθold(at∣st))，大幅加快计算

GRPO

为了让训练更快、更稳，grpo直接不使用神经网络来估计优势函数 A，而是直接使用反馈来计算。

对于一个prompt，模型先多次采样，生成多个completion，组成一个group，然后，每个completion的优势函数由 它的反馈 相对于 这个group里的平均反馈，计算得到，即 A i , t = r i − m e a n ( r ) s t d ( r ) A_{i,t}=\frac{r_i-mean(\textbf{r})}{std(\textbf{r})} Ai,t=std(r)ri−mean(r)

其目标函数可以写为

一些后续改进：

1. 除以 s t d ( r ) std(\textbf{r}) std(r)可能带来bias，例如，问题太简单，导致方差小，A就会过大。因此现在通常不除以方差
2. KL散度惩罚项对训练影响不大，因此现在的目标函数里通常不需要KL散度惩罚
3. DAPO:认为grpo的目标函数里对每个样本除以其completion的长度，这导致对于很长的completion的惩罚过小（对每个token的loss都更小），因此不除以completion的长度
4. DR-GRPO：认为DAPO依然受到response的长度的影响，因此直接除以常数
   实际训练时的操作：
   通常，我们不会对每个token计算一个单独的reward，而是对整个completion计算reward，例如，如果做对了数学题，则reward=1。因此，对于completion中的每个token，其优势函数都是一样的，即 A i , t = A i A_{i,t}=A_i Ai,t=Ai