PyTorch 深度学习实战教程-番外篇04：卷积层详解与实战指南

标签：# 深度学习 #人工智能 #神经网络 #PyTorch #卷积神经网络

引言：为什么卷积层是 CNN 的 "灵魂"？

在处理图像、视频等网格结构数据时，传统的全连接神经网络存在参数爆炸、忽视局部特征关联等问题。而卷积层（Convolutional Layer）通过局部感受野 和参数共享两大核心特性，完美解决了这些痛点，成为卷积神经网络（CNN）处理视觉任务的核心组件。本文将从基础概念到实战代码，全面解析卷积层的工作原理、核心作用及 PyTorch 实现技巧。

一、什么是卷积层？

卷积层是专门设计用于提取网格结构数据（如图片的像素网格、文本的序列网格）局部特征的神经网络层。它通过卷积操作（滑动窗口计算）对输入数据进行特征提取，相比全连接层具有以下优势：

聚焦局部特征（如图像的边缘、纹理），符合人类视觉认知规律
大幅减少参数数量，降低计算复杂度
对输入数据的平移变化具有鲁棒性

二、卷积层的工作原理：一步步看懂卷积操作

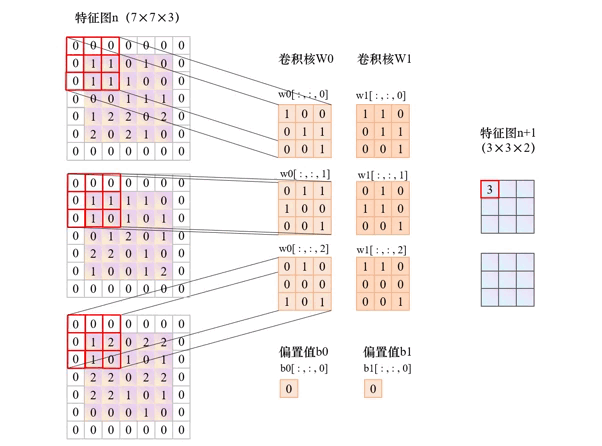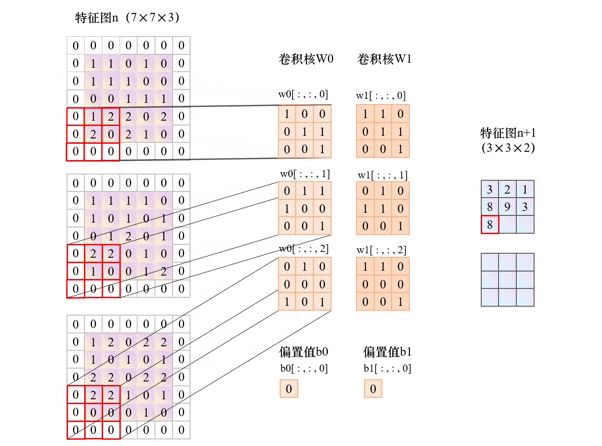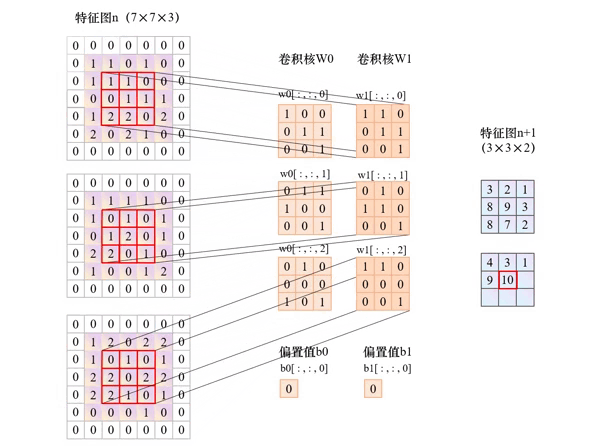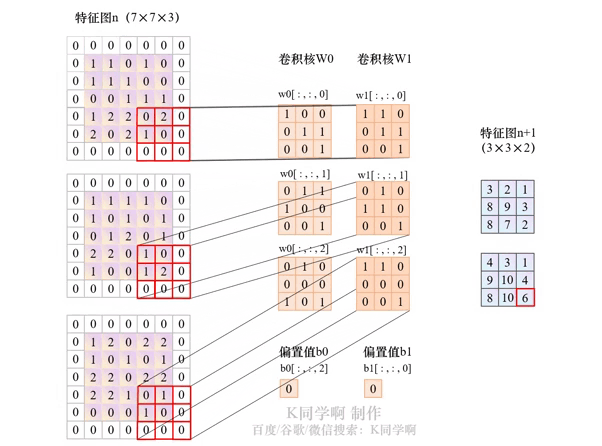
卷积层的核心是卷积操作，其过程可拆解为 4 个关键步骤，我们用具体例子直观说明：

1. 卷积核：特征提取的 "小工具"

卷积核（Kernel/Filter）是一个预设大小的矩阵（如 3×3、5×5），每个卷积核专门提取一种特定特征（如水平边缘、垂直边缘、纹理）。

例如：3×3 的卷积核可检测局部区域的边缘变化，数值分布决定了它对哪种特征敏感（如边缘检测核通常中间为正值、两侧为负值）。
卷积层的输出通道数 = 卷积核的数量（每个核输出一个特征图）。

2. 滑动窗口计算：特征提取的 "动态过程"

卷积核在输入数据上按固定步长（Stride）滑动，每次滑动时计算卷积核与对应区域的元素乘积和，结果作为输出特征图的一个像素值。

举个直观例子：假设输入是 5×5 的单通道特征图，使用 3×3 卷积核、步长 = 1：

卷积核从输入左上角开始，覆盖 (1,1)-(3,3) 区域，计算乘积和得到输出特征图的 (1,1) 像素；
按步长 = 1 向右滑动，覆盖 (1,2)-(3,4) 区域，计算得到 (1,2) 像素；
重复滑动直到覆盖整个输入区域，最终得到 3×3 的输出特征图（尺寸变化规律见下文公式）。

3. 填充（Padding）：控制输出尺寸的 "调节器"

为避免卷积操作导致特征图尺寸缩小（尤其是深层网络中），可在输入数据边缘填充 0 值，常见填充策略：

Same Padding：填充后输出尺寸与输入一致（如 3×3 卷积核 + 步长 = 1 时，padding=1 可保持尺寸）；
Valid Padding：不填充，输出尺寸随卷积操作自然缩小（默认模式）。

4. 多通道处理：彩色图像的 "特征融合"

对于 RGB 三通道图像等多输入通道数据，卷积核需与输入通道数匹配：

个卷积核包含C_in个子核（C_in为输入通道数），每个子核对应一个输入通道；
子核与对应通道卷积后求和，再叠加偏置值，得到单通道输出；
若有C_out个卷积核，最终输出C_out通道的特征图（即[C_out, H_out, W_out]）。

三、卷积层的核心作用：从理论到价值

卷积层之所以成为视觉任务的核心，源于其四大关键作用：

1. 局部特征提取：聚焦 "关键细节"

卷积核的大小（即局部感受野）决定了每次提取的局部区域范围。例如：

小卷积核（3×3）适合提取边缘、纹理等低级特征；
大卷积核（7×7）可捕捉更大范围的特征关联（但参数更多）。这种设计符合人类视觉系统 "先感知局部细节，再整合全局信息" 的规律。

2. 参数共享：大幅减少计算负担

全连接层中，每个输出神经元与所有输入神经元连接，参数量为H×W×C_in×C_out（H、W为输入尺寸）；而卷积层中，同一卷积核在输入的所有位置共享参数，参数量仅为K×K×C_in×C_out（K为卷积核大小）。 对比示例：输入为 224×224×3 的图像，若用 3×3 卷积核输出 64 通道特征：

全连接层参数量：224×224×3×64 ≈ 983 万
卷积层参数量：3×3×3×64 = 1728（仅为全连接层的 0.017%）

3. 平移不变性：特征 "在哪里都能认出来"

同一特征（如猫的耳朵）在图像的不同位置出现时，会被同一卷积核检测到。例如：无论猫的耳朵在图像左上角还是右下角，负责检测 "耳朵形状" 的卷积核都会产生高响应，这让模型对输入的平移变化更鲁棒。

4. 降维与抽象：从 "像素" 到 "语义"

通过多层卷积 + 步长控制，特征图尺寸逐步缩小（降维），同时特征从低级（边缘、纹理）抽象为高级（部件、物体）。例如：

第 1 层卷积：提取边缘、颜色块等低级特征；
第 3 层卷积：提取眼睛、鼻子等部件特征；
第 5 层卷积：提取 "猫""狗" 等完整物体特征。

四、PyTorch 卷积层实战：从参数到代码

PyTorch 的torch.nn模块提供了丰富的卷积层 API，其中nn.Conv2d是处理 2D 图像的核心工具。

1. `nn.Conv2d`核心参数详解

参数名	作用	示例
`in_channels`	输入通道数（如 RGB 图像为 3）	`in_channels=3`
`out_channels`	输出通道数（卷积核数量）	`out_channels=16`（16 个卷积核）
`kernel_size`	卷积核大小（int 或 tuple）	`kernel_size=3`（3×3）、`(3,5)`（3×5）
`stride`	滑动步长	`stride=1`（默认）、`stride=2`（尺寸减半）
`padding`	边缘填充数	`padding=1`（3×3 核保持尺寸）
`dilation`	膨胀率（扩大感受野）	`dilation=2`（3×3 核等效 5×5 感受野）
`groups`	分组卷积参数（默认 1，不分组）	`groups=2`（输入输出通道各分 2 组）
`bias`	是否添加偏置项	`bias=True`（默认添加）

2. 输出尺寸计算公式（必掌握！）

对于输入尺寸为(H, W)的特征图，卷积后输出尺寸为： \(H_{out} = \lfloor \frac{H + 2×padding - dilation×(kernel\size-1) - 1}{stride} + 1 \rfloor\) \(W{out} = \lfloor \frac{W + 2×padding - dilation×(kernel\_size-1) - 1}{stride} + 1 \rfloor\)

实例计算 ：输入H=224, W=224，kernel_size=3, stride=1, padding=1, dilation=1： \(H_{out} = (224 + 2×1 - 1×2 -1)/1 + 1 = 224\)（尺寸不变）

输入H=224, W=224，kernel_size=5, stride=2, padding=2, dilation=1： \(H_{out} = (224 + 2×2 - 1×4 -1)/2 + 1 = 112\)（尺寸减半）

3. 完整实战代码：卷积层特征提取与可视化

下面通过代码实现卷积层，并可视化卷积核、特征图的变化过程，帮助直观理解。

复制代码

import torch
import torch.nn as nn
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
from torchvision import transforms

# 1. 数据预处理：加载并转换图像
def load_image(image_path):
    """将图像转为PyTorch张量，添加批次维度"""
    # 预处理流程：调整尺寸→转Tensor→标准化（便于网络训练）
    transform = transforms.Compose([
        transforms.Resize((224, 224)),  # 统一尺寸为224×224
        transforms.ToTensor(),          # 转为Tensor，形状[C, H, W]，值范围[0,1]
        transforms.Normalize(mean=[0.5, 0.5, 0.5], std=[0.5, 0.5, 0.5])  # 标准化到[-1,1]
    ])
    image = Image.open(image_path).convert('RGB')  # 打开图像并转为RGB三通道
    image_tensor = transform(image).unsqueeze(0)   # 添加批次维度，形状变为[1, 3, 224, 224]
    return image, image_tensor

# 2. 定义卷积网络（含2个卷积层）
class ConvDemo(nn.Module):
    def __init__(self):
        super(ConvDemo, self).__init__()
        # 第1个卷积层：保持尺寸不变
        self.conv1 = nn.Conv2d(
            in_channels=3,         # 输入：RGB三通道
            out_channels=16,       # 输出：16个特征图（16个卷积核）
            kernel_size=3,         # 3×3卷积核
            stride=1,              # 步长1
            padding=1              # padding=1：保持输出尺寸=输入尺寸
        )
        # 第2个卷积层：尺寸减半
        self.conv2 = nn.Conv2d(
            in_channels=16,        # 输入：上一层的16个通道
            out_channels=8,        # 输出：8个特征图
            kernel_size=5,         # 5×5卷积核
            stride=2,              # 步长2：输出尺寸减半
            padding=2              # padding=2：配合步长2保持尺寸比例
        )
        
    def forward(self, x):
        x1 = self.conv1(x)  # 经过第1层卷积的输出
        x2 = self.conv2(x1) # 经过第2层卷积的输出
        return x1, x2

# 3. 可视化函数：展示卷积核与特征图
def visualize_results(original_image, conv1_output, conv2_output, conv1_kernels):
    plt.figure(figsize=(16, 12))  # 设置画布大小
    
    # 子图1：原始图像
    plt.subplot(3, 1, 1)
    plt.title('Original Image')
    plt.imshow(original_image)
    plt.axis('off')  # 关闭坐标轴
    
    # 子图2：第1层卷积核（前4个）
    plt.subplot(3, 2, 3)
    plt.title('First 4 Kernels of Conv1 (3×3)')
    kernels = conv1_kernels.detach().numpy()  # 转为numpy数组（脱离计算图）
    kernel_grid = np.zeros((3*3, 3*4))  # 构建3×3核的展示网格（4个核）
    for i in range(4):
        kernel = kernels[i].transpose(1, 2, 0)  # 转为[H, W, C]格式（便于显示）
        kernel = (kernel - kernel.min()) / (kernel.max() - kernel.min())  # 归一化到[0,1]
        kernel_grid[:, i*3:(i+1)*3] = kernel.reshape(9, 3)  # 排列到网格
    plt.imshow(kernel_grid, cmap='gray')
    plt.axis('off')
    
    # 子图3：第1层特征图（前4个）
    plt.subplot(3, 2, 4)
    plt.title('First 4 Feature Maps of Conv1')
    feat1 = conv1_output[0].detach().numpy()  # 取第1个样本的特征图
    feat1_grid = np.zeros((224, 224*4))  # 构建特征图展示网格
    for i in range(4):
        feat = feat1[i]
        feat = (feat - feat.min()) / (feat.max() - feat.min())  # 归一化
        feat1_grid[:, i*224:(i+1)*224] = feat  # 排列到网格
    plt.imshow(feat1_grid, cmap='gray')
    plt.axis('off')
    
    # 子图4：第2层特征图（前4个）
    plt.subplot(3, 1, 3)
    plt.title('First 4 Feature Maps of Conv2 (Downsampled)')
    feat2 = conv2_output[0].detach().numpy()
    feat2_grid = np.zeros((112, 112*4))  # 步长2，尺寸变为112×112
    for i in range(4):
        feat = feat2[i]
        feat = (feat - feat.min()) / (feat.max() - feat.min())  # 归一化
        feat2_grid[:, i*112:(i+1)*112] = feat  # 排列到网格
    plt.imshow(feat2_grid, cmap='gray')
    plt.axis('off')
    
    plt.tight_layout()  # 自动调整子图间距
    plt.show()

# 4. 主函数：执行流程
if __name__ == '__main__':
    # 加载图像（替换为你的图像路径，如'cat.jpg'）
    image, image_tensor = load_image('example.jpg')
    print(f"输入图像形状: {image_tensor.shape}")  # 输出：[1, 3, 224, 224]
    
    # 初始化模型并执行前向传播
    model = ConvDemo()
    conv1_out, conv2_out = model(image_tensor)  # 得到两层卷积的输出
    
    # 打印输出形状（验证尺寸计算）
    print(f"Conv1输出形状: {conv1_out.shape}")  # 输出：[1, 16, 224, 224]（尺寸不变）
    print(f"Conv2输出形状: {conv2_out.shape}")  # 输出：[1, 8, 112, 112]（尺寸减半）
    
    # 获取第1层卷积核（权重参数）
    conv1_kernels = model.conv1.weight  # 形状：[16, 3, 3, 3]（16个3×3×3的核）
    
    # 可视化结果
    visualize_results(
        original_image=image,
        conv1_output=conv1_out,
        conv2_output=conv2_out,
        conv1_kernels=conv1_kernels
    )

4. 代码关键步骤解析

数据预处理 ：通过transforms将图像转为网络可接受的张量格式，标准化操作可加速模型收敛。
卷积层设计 ：
- conv1使用padding=1配合stride=1，确保输出尺寸与输入一致（224×224）；
- conv2使用stride=2实现降维，padding=2保证尺寸平滑缩小至 112×112。
可视化解读 ：
- 卷积核：每个 3×3 的矩阵是特征提取 "模板"，不同核关注不同特征；
- 特征图：第 1 层保留较多细节，第 2 层尺寸缩小且特征更抽象（已整合局部信息）。

五、总结与实践建议

卷积层通过局部感受野和参数共享，实现了对网格数据的高效特征提取，是 CNN 处理视觉任务的核心。掌握卷积层需重点关注：

参数设计 ：根据任务需求调整kernel_size（小核适合细节，大核适合全局）、stride（控制降维速度）、padding（保持尺寸或降维）；
尺寸计算：熟练运用输出尺寸公式，避免网络设计中出现尺寸不匹配问题；
实战技巧：多层卷积逐步抽象特征，通常配合池化层进一步降维（后续文章将详解）。