摘要
在文章 Uniswap 流动性机制及相关数学原理分析(以下简称原理分析)中,我们详细地推导了流动性和交易相关公式,这些公式都是在假设没有手续费和协议费的情况之下得出的。现实中,Uniswap 是存在手续费和协议费的,引入这些费率后,公式推导过程依然不变,但形式需要相应调整。Uniswap 从每笔交易中收取手续费和协议费,因此最符合直觉的记账方式应当是每笔交易均记录相关费用,这在中心化交易所里是可以接受的,但是在区块链上,任何额外的计算都需要支付 gas 费用,所以 Uniswap 只记录必要的状态,只在需要时才从这些状态计算相关费用,避免额外的成本。这种记账方式省去了不必要的计算,代价就是不直观且更难理解,因此这篇文章将详细剖析 Uniswap 中手续费和协议费机制,包括相关数学公式的推导以及设计和实现方式。此外,Uniswap 已从 V2 升级至了 V3 版本(截至文章写作时,V4 也已经发布,但对于费率机制来说 V3 和 V4 可看作一个版本),V2 和 V3 采用了完全不同的记账和结算方式,这篇文章也会一一分析。
V2 中的手续费和协议费
Uniswap V2 中规定每笔交易收取 3‰(千分之三)的手续费。但请注意,这个手续费不是直接从被交易的资产中扣除 3‰。假设交易者想要使用 <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ x \Delta{x} </math>Δx 的资产换取 <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ y \Delta{y} </math>Δy 的资产,那么手续费的计算过程如下(为了便于公式表达,手续费率使用 <math xmlns="http://www.w3.org/1998/Math/MathML"> γ \gamma </math>γ 表示,现实中 <math xmlns="http://www.w3.org/1998/Math/MathML"> γ = 0.003 \gamma = 0.003 </math>γ=0.003):
- 从交易者提供的资产数量里扣除 <math xmlns="http://www.w3.org/1998/Math/MathML"> γ Δ x \gamma\Delta{x} </math>γΔx,也就是说参与交易的部分只有 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( 1 − γ ) Δ x (1-\gamma)\Delta{x} </math>(1−γ)Δx
- 根据乘积常数规则,计算出交易者可换取的资产数量 <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ y \Delta{y} </math>Δy
- 若不做扣除,根据原理分析中的公式 (36),交易者可换取更多的资产,假设为 <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ y ′ \Delta{y'} </math>Δy′,则 <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ y ′ − Δ y \Delta{y'} - \Delta{y} </math>Δy′−Δy 就是交易者支付的手续费
需要注意的是,只是在计算交易者可换取的资产数量 <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ y \Delta{y} </math>Δy 时扣除 <math xmlns="http://www.w3.org/1998/Math/MathML"> γ Δ x \gamma\Delta{x} </math>γΔx,但交易完成时,交易者向池子里转入的资产数量仍为 <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ x \Delta{x} </math>Δx。
设交易前池子的乘积常数为 <math xmlns="http://www.w3.org/1998/Math/MathML"> k k </math>k,则上述 1,2 写成数学公式表达就是:
<math xmlns="http://www.w3.org/1998/Math/MathML"> ( x + ( 1 − γ ) Δ x ) ( y − Δ y ) = k ( 1 ) (x+(1-\gamma)\Delta{x})(y-\Delta{y}) = k \qquad(1) </math>(x+(1−γ)Δx)(y−Δy)=k(1)
解得:
<math xmlns="http://www.w3.org/1998/Math/MathML"> Δ y = ( 1 − γ ) Δ x x + ( 1 − γ ) Δ x y ( 2 ) \Delta{y} = \frac{(1-\gamma)\Delta{x}}{x+(1-\gamma)\Delta{x}}y \qquad(2) </math>Δy=x+(1−γ)Δx(1−γ)Δxy(2)
从原理分析中的公式 (36) 我们知道无手续费时,交易者本应获得的资产数量为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> Δ y ′ = Δ x x + Δ x y ( 3 ) \Delta{y'} = \frac{\Delta{x}}{x + \Delta{x}}y \qquad(3) </math>Δy′=x+ΔxΔxy(3)
两式相除并化简,最终可以得到:
<math xmlns="http://www.w3.org/1998/Math/MathML"> Δ y Δ y ′ = 1 − γ x x + ( 1 − γ ) Δ x = 1 − γ 1 + ( 1 − γ ) Δ x x ( 4 ) \frac{\Delta{y}}{\Delta{y'}} = 1-\frac{\gamma{x}}{x+(1-\gamma)\Delta{x}} = 1 - \frac{\gamma}{1 + (1-\gamma)\frac{\Delta{x}}{x}} \qquad(4) </math>Δy′Δy=1−x+(1−γ)Δxγx=1−1+(1−γ)xΔxγ(4)
从公式 (4) 中可以看出,除非 <math xmlns="http://www.w3.org/1998/Math/MathML"> γ = 0 \gamma = 0 </math>γ=0,否则比值恒小于 1,其差值部分就是池子收取的手续费。举个例子,假设 <math xmlns="http://www.w3.org/1998/Math/MathML"> x = 1000 x = 1000 </math>x=1000, <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ x = 1 \Delta{x} = 1 </math>Δx=1,代入得:
<math xmlns="http://www.w3.org/1998/Math/MathML"> 1 − 0.003 × 10000 10000 + ( 1 − 0.003 ) × 1 ≈ 0.9970003 1 - \frac{0.003\times10000}{10000 + (1-0.003)\times1} \approx 0.9970003 </math>1−10000+(1−0.003)×10.003×10000≈0.9970003
可以看出来,结果非常接近手续费率 <math xmlns="http://www.w3.org/1998/Math/MathML"> γ \gamma </math>γ,从公式 (4) 也可以看出来, <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ x x \frac{\Delta{x}}{x} </math>xΔx 越小,其值就越接近费率 <math xmlns="http://www.w3.org/1998/Math/MathML"> γ \gamma </math>γ。
值得注意的是,交易完成后,池子储量的乘积常数会变大一点点,不再是 <math xmlns="http://www.w3.org/1998/Math/MathML"> k k </math>k,而是:
<math xmlns="http://www.w3.org/1998/Math/MathML"> k ′ = ( x + Δ x ) ( y − ( 1 − γ ) Δ x x + ( 1 − γ ) Δ x y ) = k x + Δ x x + ( 1 − γ ) Δ x > k k' = (x + \Delta{x})(y - \frac{(1-\gamma)\Delta{x}}{x+(1-\gamma)\Delta{x}}y) = k\frac{x+\Delta{x}}{x+(1-\gamma)\Delta{x}} > k </math>k′=(x+Δx)(y−x+(1−γ)Δx(1−γ)Δxy)=kx+(1−γ)Δxx+Δx>k
结果很好理解,如果没有手续费,交易后储量乘积肯定还是 <math xmlns="http://www.w3.org/1998/Math/MathML"> k k </math>k,但是因为手续费的存在,转出去的 <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ y \Delta{y} </math>Δy 扣留了一部分在池子里,自然使得乘积的结果变大,这扣留的一部分,就是手续费的来源。
在原理分析中我们推导了提供流动性时,所需资产数量分别为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> Δ x 1 = Δ L L 1 x 1 \Delta{x_1} = \frac{\Delta{L}}{L_1}x_1 </math>Δx1=L1ΔLx1
<math xmlns="http://www.w3.org/1998/Math/MathML"> Δ y 1 = Δ L L 1 y 1 \Delta{y_1} = \frac{\Delta{L}}{L_1}y_1 </math>Δy1=L1ΔLy1
其中 <math xmlns="http://www.w3.org/1998/Math/MathML"> x 1 x_1 </math>x1 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> y 1 y_1 </math>y1 分别是此时资产 X 和 Y 的储量, <math xmlns="http://www.w3.org/1998/Math/MathML"> L 1 L_1 </math>L1 是此时流动性代币的总供应量。
两式相乘可得:
<math xmlns="http://www.w3.org/1998/Math/MathML"> Δ x 1 Δ y 1 = Δ L 2 L 1 2 k 1 \Delta{x_1}\Delta{y_1}=\frac{\Delta{L}^2}{L_1^2}k_1 </math>Δx1Δy1=L12ΔL2k1
开方得:
<math xmlns="http://www.w3.org/1998/Math/MathML"> Δ x 1 Δ y 1 = Δ L L 1 k 1 ( 5 ) \sqrt{\Delta{x_1}\Delta{y_1}} = \frac{\Delta{L}}{L_1}\sqrt{k_1} \qquad(5) </math>Δx1Δy1 =L1ΔLk1 (5)
移除流动性时,可提取的资产数量:
<math xmlns="http://www.w3.org/1998/Math/MathML"> Δ x 2 = Δ L L 2 x 2 \Delta{x}_2 = \frac{\Delta{L}}{L_2}x_2 </math>Δx2=L2ΔLx2
<math xmlns="http://www.w3.org/1998/Math/MathML"> Δ y 2 = Δ L L 2 y 2 \Delta{y}_2 = \frac{\Delta{L}}{L_2}y_2 </math>Δy2=L2ΔLy2
两式相乘可得:
<math xmlns="http://www.w3.org/1998/Math/MathML"> Δ x 2 Δ y 2 = Δ L 2 L 2 2 k 2 \Delta{x_2}\Delta{y_2}=\frac{\Delta{L}^2}{L_2^2}k_2 </math>Δx2Δy2=L22ΔL2k2
开方得:
<math xmlns="http://www.w3.org/1998/Math/MathML"> Δ x 2 Δ y 2 = Δ L L 2 k 2 ( 6 ) \sqrt{\Delta{x_2}\Delta{y_2}} = \frac{\Delta{L}}{L_2}\sqrt{k_2} \qquad(6) </math>Δx2Δy2 =L2ΔLk2 (6)
其中 <math xmlns="http://www.w3.org/1998/Math/MathML"> L 2 L_2 </math>L2 是此时池子总流动性代币供应量, <math xmlns="http://www.w3.org/1998/Math/MathML"> k 2 k_2 </math>k2 是此时池子储量的乘积。请注意,前面已经分析过,如果有交易, <math xmlns="http://www.w3.org/1998/Math/MathML"> k k </math>k 会增大。因此, <math xmlns="http://www.w3.org/1998/Math/MathML"> L L </math>L 不一定等于 <math xmlns="http://www.w3.org/1998/Math/MathML"> k k </math>k。
公式 (6) 和 (5) 相减,可得:
<math xmlns="http://www.w3.org/1998/Math/MathML"> Δ x 2 Δ y 2 − Δ x 1 Δ y 1 = Δ L L 2 k 2 − Δ L L 1 k 1 ( 7 ) \sqrt{\Delta{x_2}\Delta{y_2}} - \sqrt{\Delta{x_1}\Delta{y_1}} = \frac{\Delta{L}}{L_2}\sqrt{k_2} - \frac{\Delta{L}}{L_1}\sqrt{k_1} \qquad(7) </math>Δx2Δy2 −Δx1Δy1 =L2ΔLk2 −L1ΔLk1 (7)
公式 (7) 说明,在流动性意义下( <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ x Δ y \sqrt{\Delta{x}\Delta{y}} </math>ΔxΔy ),流动性提供者(Liquidity Provider,以下简称 LP)赚取的交易手续费实际上是池子乘积常数的相对增量值。而且请注意,在 <math xmlns="http://www.w3.org/1998/Math/MathML"> k 1 k_1 </math>k1 变到 <math xmlns="http://www.w3.org/1998/Math/MathML"> k 2 k_2 </math>k2, <math xmlns="http://www.w3.org/1998/Math/MathML"> L 1 L_1 </math>L1 变到 <math xmlns="http://www.w3.org/1998/Math/MathML"> L 2 L_2 </math>L2 的过程中,可能包含各种交易以及流动性的添加和移除。公式 (7) 的值并不能保证绝对为正数,这也从另一方面体现了所谓的无常损失。
接下来我们讨论协议费,协议费可以看成一个特殊的 LP 来分手续费,Uniswap 规定协议可拿走手续费的一定比例 <math xmlns="http://www.w3.org/1998/Math/MathML"> ϕ \phi </math>ϕ,现实中 <math xmlns="http://www.w3.org/1998/Math/MathML"> ϕ = 0.05 \phi = 0.05% </math>ϕ=0.05。为了节省 gas,协议费不是在单笔交易中记录,而是在 LP 添加或者移除流动性时记录,记录方式为给协议地址铸造流动性代币 <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ L \Delta{L} </math>ΔL,稀释其他 LP 的份额来实现。
那么现在问题变为,新铸多少流动性代币,可以使得协议地址分得规定数量的协议费呢?
假设需要新铸 <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ L \Delta{L} </math>ΔL 的代币,一方面根据公式 (7),由于协议费是在每次添加或者移除流动性时记录,在此过程中只有交易发生,因此 <math xmlns="http://www.w3.org/1998/Math/MathML"> L 2 = L 1 L_2 = L_1 </math>L2=L1,故公式 (7) 变为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> Δ x 2 Δ y 2 − Δ x 1 Δ y 1 = Δ L L 1 k 2 − Δ L L 1 k 1 = Δ L L 1 ( k 2 − k 1 ) ( 8 ) \sqrt{\Delta{x_2}\Delta{y_2}} - \sqrt{\Delta{x_1}\Delta{y_1}} = \frac{\Delta{L}}{L_1}\sqrt{k_2} - \frac{\Delta{L}}{L_1}\sqrt{k_1} = \frac{\Delta{L}}{L_1}(\sqrt{k_2}-\sqrt{k_1}) \qquad(8) </math>Δx2Δy2 −Δx1Δy1 =L1ΔLk2 −L1ΔLk1 =L1ΔL(k2 −k1 )(8)
公式 (8) 说明,在只有交易发生的情况下,LP 赚取的手续费(流动性意义下)根据其贡献流动性的份额,分走常数乘积的增量 <math xmlns="http://www.w3.org/1998/Math/MathML"> k 2 − k 1 \sqrt{k_2}-\sqrt{k_1} </math>k2 −k1 ,所以协议需分走的量为 <math xmlns="http://www.w3.org/1998/Math/MathML"> ϕ ( k 2 − k 1 ) \phi(\sqrt{k_2}-\sqrt{k_1}) </math>ϕ(k2 −k1 )。
另一方面,根据公式 (6),给协议地址新铸 <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ L \Delta{L} </math>ΔL 流动性代币后,此时若其撤走流动性,其可以获得的代币数量等于 <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ L L 1 + Δ L k 2 \frac{\Delta{L}}{L_1 + \Delta{L}}\sqrt{k_2} </math>L1+ΔLΔLk2
因此可得:
<math xmlns="http://www.w3.org/1998/Math/MathML"> Δ L L 1 + Δ L k 2 = ϕ ( k 2 − k 1 ) \frac{\Delta{L}}{L_1 + \Delta{L}}\sqrt{k_2}=\phi(\sqrt{k_2} - \sqrt{k_1}) </math>L1+ΔLΔLk2 =ϕ(k2 −k1 )
解得:
<math xmlns="http://www.w3.org/1998/Math/MathML"> Δ L = k 2 − k 1 ( 1 ϕ − 1 ) k 2 + k 1 L 1 ( 9 ) \Delta{L} = \frac{\sqrt{k_2} - \sqrt{k_1}}{(\frac{1}{\phi} - 1)\sqrt{k_2} + \sqrt{k_1}}L_1 \qquad(9) </math>ΔL=(ϕ1−1)k2 +k1 k2 −k1 L1(9)
公式 (9) 即为白皮书中的公式 (6),只是将 <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ L \Delta{L} </math>ΔL 换为 <math xmlns="http://www.w3.org/1998/Math/MathML"> s m s_m </math>sm, <math xmlns="http://www.w3.org/1998/Math/MathML"> L 1 L_1 </math>L1 换为 <math xmlns="http://www.w3.org/1998/Math/MathML"> s 1 s_1 </math>s1。
以上即为 Uniswap V2 手续费和协议费的机制,总结一下:
- LP 赚取的手续费分成由公式 (7) 给出。当然在实现上,LP 撤走流动性时,所提取的代币数量直接通过原理分析中的公式 (22) 和 (23) 计算,手续费分成已含在提取的代币中。
- 若池子启用了协议费,每次 LP 添加或者移除流动性是,根据公式 (9) 为协议地址铸造流动性代币,则可按规定收取协议费。
可以看到,为了计算手续费和协议费,我们需要各种数学公式推导,虽然优雅简洁,但是不容易理解。
接下来我们设计一套更加直观的记账方式,新记账方式的核心是记录每单位流动性可分配的手续费以及总协议费。
由于交易方向不同,抵扣手续费所使用的资产也不同。为此,我们设置了两个全局变量:feeGrowthGlobal0 和 feeGrowthGlobal1,分别用于记录每单位流动性可分配到的资产 X 手续费和资产 Y 手续费。为了方便,后续的表述中不区分资产种类,统称为 feeGrowthGlobal。
同理,再设置 2 个全局变量记录总的协议费,分别为 protocolFee0 和 protocolFee1,统称为 protocolFee。
每一次交易(swap),设总手续费是 feeAmount,从总的手续费中拿走一部分 protocalFeeAmount 作为协议费,那么 protocolFee += protocalFeeAmount。总的流动性是 LiquidityGlobal,那么交易后 feeGrowthGlobal += (feeAmount - protocalFeeAmount) / LiquidityGlobal。
以上只是记录了总的每单位流动性可分配的手续费收益,还需要根据每个 LP 提供的流动性占比,记录其可分配到的手续费收益。我们把 LP 提供的流动性叫做 Position,Position 中记录了:
- LP 提供的流动性数量
liquidity - LP 上一次提取手续费收益时每单位流动性可分配的收益,统称为
feeGrowthGlobalLast,变量的初始值设置为当前feeGrowthGlobal。
那么 LP 可分配的手续费收益就是等于 (feeGrowthGlobal - feeGrowthGlobalLast) * liquidity。可以看到,如果 LP 添加流动性后没有交易发生,此时 feeGrowthGlobal - feeGrowthGlobalLast 等于 0,可分配的收益为 0。此后随着交易发生,feeGrowthGlobal 不断累积增大,LP 就可以分配到其该得的手续费收益。
为什么要设计上面这种记账方式呢?因为随着 V3 引入了范围流动性,再用公式计算就变得很复杂了,V3 中采用的就是上面这种更加直观的记账方式。
V3 中的手续费和协议费
先来说明实践中 V3 对价格的处理方式。原理分析中说了 V3 将流动性限定在一个价格范围。如果价格是连续的,范围两端的价格可以是任意实数,这样价格就会分的太散。所以 V3 将价格离散化,价格只能在这些离散化的点跳动,而不是连续变化。
这样做有一定合理性,实际上中心化交易所也会这样做。盘口挂单时,订单不能是任意价格,通常都有一个最小价格变动单位,例如 BTC 卖一价为 10000.0,最小变动单位是 0.1,那么卖二价格可以挂 10000.10,但 10000.05 的价格永远不会出现。
Uniswap 将离散价格对应的点叫做 tick, tick <math xmlns="http://www.w3.org/1998/Math/MathML"> i i </math>i 和价格的映射关系如下:
<math xmlns="http://www.w3.org/1998/Math/MathML"> P i = 1.000 1 i P_i = 1.0001^i </math>Pi=1.0001i
由于 tick 和价格之间是一一对应的,文章后续表述中会不加区分地混用价格和 tick 。例如价格范围,也可以说成是 tick 范围,以及当前资产价格 <math xmlns="http://www.w3.org/1998/Math/MathML"> P P </math>P、其平方根 <math xmlns="http://www.w3.org/1998/Math/MathML"> P \sqrt{P} </math>P 和当前 tick 是一回事。
图 1 是价格离散化后,流动性池的一个示意。有 2 个 LP 在 tick <math xmlns="http://www.w3.org/1998/Math/MathML"> i 1 i_1 </math>i1 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> i 2 i_2 </math>i2 间分别添加了流动性 <math xmlns="http://www.w3.org/1998/Math/MathML"> L 1 L_1 </math>L1 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> L 2 L_2 </math>L2;另一个 LP 在 <math xmlns="http://www.w3.org/1998/Math/MathML"> i 3 i_3 </math>i3 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> i 4 i_4 </math>i4 间添加了流动性 <math xmlns="http://www.w3.org/1998/Math/MathML"> L 3 L_3 </math>L3。区间 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( i 1 , i 2 ) (i_1,i_2) </math>(i1,i2) 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( i 3 , i 4 ) (i_3,i_4) </math>(i3,i4) 有一段重合,根据流动性叠加原理,重叠部分流动性为 <math xmlns="http://www.w3.org/1998/Math/MathML"> L 1 + L 2 + L 3 L_1 + L_2 + L_3 </math>L1+L2+L3。图中还标出了当前价格对应的 tick <math xmlns="http://www.w3.org/1998/Math/MathML"> i c i_c </math>ic。 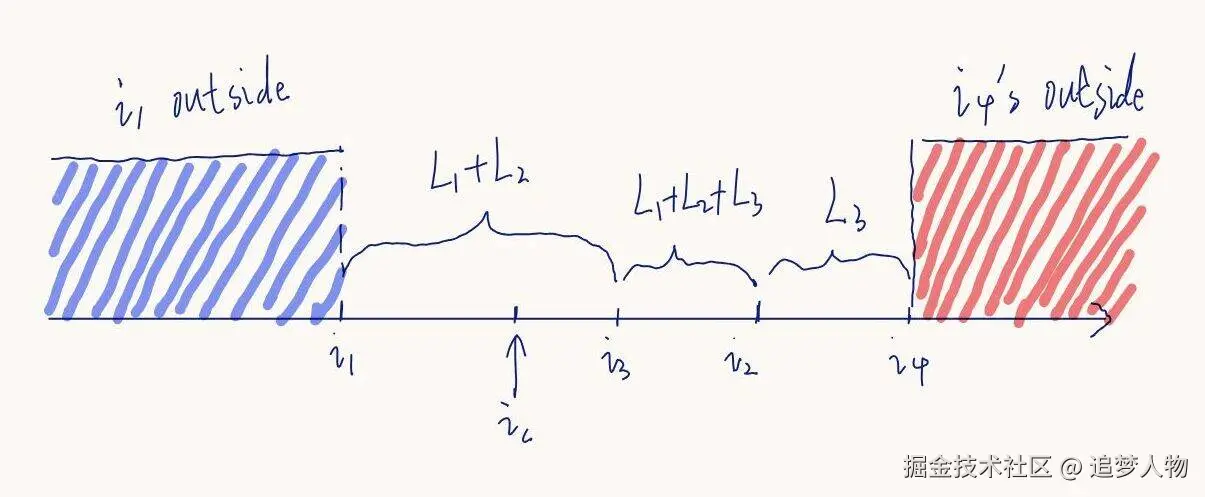 图 1
图 1
在流动性区间内发生的交易将在该区间内产生手续费,所有在此区间添加了流动性的 LP 都将获得手续费分成,所以现在问题的关键是如何计算流动性区间,例如 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( i 1 , i 2 ) (i_1,i_2) </math>(i1,i2) 或 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( i 3 , i 4 ) (i_3,i_4) </math>(i3,i4) 的手续费。
最简单的方法就是直接记录。即定义一个 map,将区间上下边界对应的 tick 区间作为键,值记录这个区间相关的所有信息,包括在这个区间内累积的手续费。这种方式很直观,但是缺点也很明显,一是很多区间可能共享同一个边界 tick,造成一定重复。二是在当前价格 <math xmlns="http://www.w3.org/1998/Math/MathML"> i c i_c </math>ic 发生的交易,需要遍历所有包含此价格的区间,更新其手续费。
Uniswap 采用了另外的记账方式,不是记录区间信息,而只记录区间边界 tick 的信息。当需要知道某个区间的信息时,从区间边界 tick 的信息就可以计算出区间的信息。例如我们首先记一个全局手续费变量 <math xmlns="http://www.w3.org/1998/Math/MathML"> f g f_g </math>fg,这是整个池子累积的手续费。此外,我们还记录 <math xmlns="http://www.w3.org/1998/Math/MathML"> i 1 i_1 </math>i1 左边的手续费 <math xmlns="http://www.w3.org/1998/Math/MathML"> f b ( i 1 ) f_b(i_1) </math>fb(i1),以及 <math xmlns="http://www.w3.org/1998/Math/MathML"> i 2 i_2 </math>i2 右边的手续费 <math xmlns="http://www.w3.org/1998/Math/MathML"> f a ( i 2 ) f_a(i_2) </math>fa(i2),那么 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( i 1 , i 2 ) (i_1, i_2) </math>(i1,i2) 区间累积的手续费就等于 <math xmlns="http://www.w3.org/1998/Math/MathML"> f g − f b ( i 1 ) − f a ( i 2 ) f_g - f_b(i_1) - f_a(i_2) </math>fg−fb(i1)−fa(i2)。当然这种方式仍然存在缺点,就是需要同时记录一个 tick 左边和右边累积的手续费。Uniswap 进一步使用了更加巧妙的方式,这种方式只需记录单边手续费就足够了。
Uniswap 引入一个外边 (outside) 的概念,从图 1 来看,一个 tick 将区域分割成左边和右边(Uniswap V3 白皮书中称为下边 below 和上边 above ,我们这里为了直观起见叫左边和右边,但依然沿用白皮书中的公式下标),那么外边就是不含当前价格的一边。例如图 1 中, <math xmlns="http://www.w3.org/1998/Math/MathML"> i 1 i_1 </math>i1 的外边是蓝色区域,而 <math xmlns="http://www.w3.org/1998/Math/MathML"> i 4 i_4 </math>i4 的外边是红色区域, <math xmlns="http://www.w3.org/1998/Math/MathML"> i 2 i_2 </math>i2 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> i 3 i_3 </math>i3 的外边同理。
一个 tick 左边和右边的手续费可以通过外边表示。以 <math xmlns="http://www.w3.org/1998/Math/MathML"> i 1 i_1 </math>i1 为例,其左边手续费 <math xmlns="http://www.w3.org/1998/Math/MathML"> f b ( i 1 ) f_b(i_1) </math>fb(i1) 就等于外边的手续费 <math xmlns="http://www.w3.org/1998/Math/MathML"> f o ( i 1 ) f_o(i_1) </math>fo(i1),而右边手续费 <math xmlns="http://www.w3.org/1998/Math/MathML"> f a ( i 1 ) = f g − f o ( i 1 ) f_a(i_1) = f_g - f_o(i_1) </math>fa(i1)=fg−fo(i1),即全局手续费减去外边手续费。对 <math xmlns="http://www.w3.org/1998/Math/MathML"> i 2 i_2 </math>i2 则刚好相反,其右边手续费 <math xmlns="http://www.w3.org/1998/Math/MathML"> f a ( i 2 ) = f o ( i 2 ) f_a(i_2) = f_o(i_2) </math>fa(i2)=fo(i2),左边手续费 <math xmlns="http://www.w3.org/1998/Math/MathML"> f b ( i 2 ) = f g − f o ( i 2 ) f_b(i_2) = f_g - f_o(i_2) </math>fb(i2)=fg−fo(i2)。总结起来,对于任意 tick <math xmlns="http://www.w3.org/1998/Math/MathML"> i i </math>i,如果其外边的手续费为 <math xmlns="http://www.w3.org/1998/Math/MathML"> f o ( i ) f_o(i) </math>fo(i),则左边手续费 <math xmlns="http://www.w3.org/1998/Math/MathML"> f b ( i ) f_b(i) </math>fb(i) 和右边手续费 <math xmlns="http://www.w3.org/1998/Math/MathML"> f a ( i ) f_a(i) </math>fa(i) 分别为:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> f a ( i ) = { f g − f o ( i ) i c ≥ i f o ( i ) i c < i f_a(i) = \begin{cases} f_g - f_o(i) & i_c \geq i \\ f_o(i) & i_c < i \end{cases} </math>fa(i)={fg−fo(i)fo(i)ic≥iic<i
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> f b ( i ) = { f o ( i ) i c ≥ i f g − f o ( i ) i c < i f_b(i) = \begin{cases} f_o(i) & i_c \geq i \\ f_g - f_o(i) & i_c < i \end{cases} </math>fb(i)={fo(i)fg−fo(i)ic≥iic<i
其中 <math xmlns="http://www.w3.org/1998/Math/MathML"> i c i_c </math>ic 为当前价格对应的 tick。上述公式实际上就是白皮书中的公式 (6.17) 和 (6.18)。
对任意区间 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( i l , i u ) (i_l, i_u) </math>(il,iu),可计算出累积手续费为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> f r = f g − f b ( i l ) − f a ( i u ) f_r = f_g - f_b(i_l) - f_a(i_u) </math>fr=fg−fb(il)−fa(iu)
上述公式实际上就是白皮书中的公式 (6.19)
外边手续费的初始值设置规则如下:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> f o : = { f g i c ≥ i 0 i c < i f_o := \begin{cases} f_g & i_c \geq i \\ 0 & i_c < i \end{cases} </math>fo:={fg0ic≥iic<i
按白皮书中说的就是:
When <math xmlns="http://www.w3.org/1998/Math/MathML"> f o f_o </math>fo is initialized for a tick <math xmlns="http://www.w3.org/1998/Math/MathML"> i i </math>i, the value---by convention---is chosen as if all of the fees earned to date had occurred below that tick. 当为一个 tick <math xmlns="http://www.w3.org/1998/Math/MathML"> i i </math>i 初始化 <math xmlns="http://www.w3.org/1998/Math/MathML"> f o f_o </math>fo 时,按照惯例,其取值应设定为仿佛截至目前赚取的所有费用都发生在该 tick 左边。
这样可以保证算出的 tick 区间初始累积的手续费是 0,同时也不会影响已初始化区间的手续费。要注意,已经初始化过的 tick 有新的流动性加入时,不需要再更新外边手续费的值。
值得注意的是,如果一笔交易在当前价格 <math xmlns="http://www.w3.org/1998/Math/MathML"> i c i_c </math>ic 发生,理论上来说需要更新所有外边包含 <math xmlns="http://www.w3.org/1998/Math/MathML"> i c i_c </math>ic 的 tick,但是实际上没有必要。看图 2 的例子,交易发生前价格为 <math xmlns="http://www.w3.org/1998/Math/MathML"> i c i_c </math>ic,全局手续费为 <math xmlns="http://www.w3.org/1998/Math/MathML"> f g f_g </math>fg,区间手续费为 <math xmlns="http://www.w3.org/1998/Math/MathML"> f g − f o ( i l ) − f o ( i u ) f_g - f_o(i_l) - f_o(i_u) </math>fg−fo(il)−fo(iu)。交易发生后,价格变为 <math xmlns="http://www.w3.org/1998/Math/MathML"> i c ′ i_c' </math>ic′,设交易手续费为 <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ f \Delta{f} </math>Δf,则全局手续费变为 <math xmlns="http://www.w3.org/1998/Math/MathML"> f g + Δ f f_g+\Delta{f} </math>fg+Δf,区间手续费变为 <math xmlns="http://www.w3.org/1998/Math/MathML"> f g + Δ f − f o ( i l ) − f o ( i u ) f_g + \Delta{f} - f_o(i_l) - f_o(i_u) </math>fg+Δf−fo(il)−fo(iu),同交易前区间手续费的差值为 <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ f \Delta{f} </math>Δf,这正是交易使得区间增加的手续费。 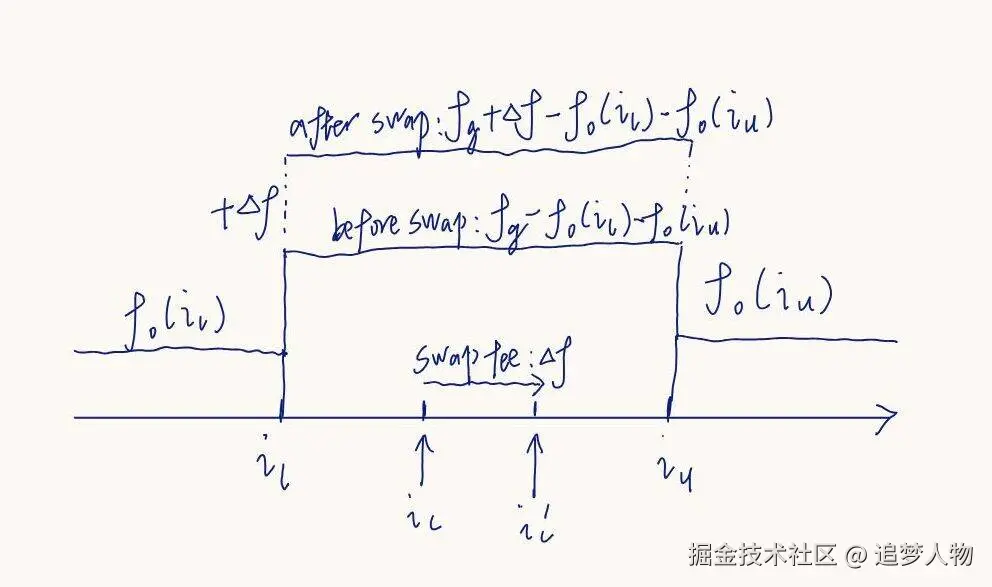 图 2
图 2
那么什么时候需要更新 tick 的 <math xmlns="http://www.w3.org/1998/Math/MathML"> f o f_o </math>fo 呢?答案是 tick 被穿越后。tick 被穿越后,对这个 tick 来说,外边发生了反向,因此按如下公式更新 <math xmlns="http://www.w3.org/1998/Math/MathML"> f o f_o </math>fo 的值:
<math xmlns="http://www.w3.org/1998/Math/MathML"> f o : = f g − f o ( 10 ) f_o := f_g - f_o \qquad(10) </math>fo:=fg−fo(10)
为什么是按照这个公式来更新 <math xmlns="http://www.w3.org/1998/Math/MathML"> f o f_o </math>fo?我们以图 3 为例进行说明。全局手续费为 <math xmlns="http://www.w3.org/1998/Math/MathML"> f g f_g </math>fg, <math xmlns="http://www.w3.org/1998/Math/MathML"> i u i_u </math>iu 外侧手续费为 <math xmlns="http://www.w3.org/1998/Math/MathML"> f o ( i u ) f_o(i_u) </math>fo(iu),在当前价格未穿越 <math xmlns="http://www.w3.org/1998/Math/MathML"> i u i_u </math>iu 仍为 <math xmlns="http://www.w3.org/1998/Math/MathML"> i c i_c </math>ic 前, <math xmlns="http://www.w3.org/1998/Math/MathML"> i u i_u </math>iu 外侧为其右边区域,此外我们也可以求得 <math xmlns="http://www.w3.org/1998/Math/MathML"> i u i_u </math>iu 左边区域的手续费为 <math xmlns="http://www.w3.org/1998/Math/MathML"> f g − f o ( i u ) f_g - f_o(i_u) </math>fg−fo(iu)。假设前几笔交易都在区间内进行,使得区间手续费增加了 <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ f \Delta{f} </math>Δf,之前已经讨论过, <math xmlns="http://www.w3.org/1998/Math/MathML"> i u i_u </math>iu 未被穿越,其外侧手续费仍然为 <math xmlns="http://www.w3.org/1998/Math/MathML"> f o ( i u ) f_o(i_u) </math>fo(iu) 不变,只是全局手续费 <math xmlns="http://www.w3.org/1998/Math/MathML"> f g f_g </math>fg 变为 <math xmlns="http://www.w3.org/1998/Math/MathML"> f g + Δ f f_g+\Delta{f} </math>fg+Δf,计算得出 <math xmlns="http://www.w3.org/1998/Math/MathML"> i u i_u </math>iu 左边的手续费变为 <math xmlns="http://www.w3.org/1998/Math/MathML"> f g + Δ f − f o ( i u ) f_g + \Delta{f} - f_o(i_u) </math>fg+Δf−fo(iu)。随后,一笔交易使得 <math xmlns="http://www.w3.org/1998/Math/MathML"> i c i_c </math>ic 穿过 <math xmlns="http://www.w3.org/1998/Math/MathML"> i u i_u </math>iu 到达 <math xmlns="http://www.w3.org/1998/Math/MathML"> i c ′ i_c' </math>ic′,该笔手续费为 <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ f 2 \Delta{f}_2 </math>Δf2,此时全局手续费 <math xmlns="http://www.w3.org/1998/Math/MathML"> f g f_g </math>fg 变为 <math xmlns="http://www.w3.org/1998/Math/MathML"> f g + Δ f + Δ f 2 f_g+\Delta{f}+\Delta{f}_2 </math>fg+Δf+Δf2, <math xmlns="http://www.w3.org/1998/Math/MathML"> i u i_u </math>iu 左边的手续费变为 <math xmlns="http://www.w3.org/1998/Math/MathML"> f g + Δ f + Δ f 2 − f o ( i u ) f_g + \Delta{f}+\Delta{f}_2 - f_o(i_u) </math>fg+Δf+Δf2−fo(iu),而此时 <math xmlns="http://www.w3.org/1998/Math/MathML"> i u i_u </math>iu 的左侧变为了外侧,因此:
<math xmlns="http://www.w3.org/1998/Math/MathML"> f o ( i u ) : = f g + Δ f + Δ f 2 − f o ( i u ) f_o(i_u) := f_g + \Delta{f}+\Delta{f_2} - f_o(i_u) </math>fo(iu):=fg+Δf+Δf2−fo(iu)
注意这里 <math xmlns="http://www.w3.org/1998/Math/MathML"> f g : = f g + Δ f + Δ f 2 f_g := f_g + \Delta{f}+\Delta{f_2} </math>fg:=fg+Δf+Δf2 是 <math xmlns="http://www.w3.org/1998/Math/MathML"> i u i_u </math>iu 被穿越后最新的全局手续费,赋值式子左边的 <math xmlns="http://www.w3.org/1998/Math/MathML"> f o ( i u ) f_o(i_u) </math>fo(iu) 是 <math xmlns="http://www.w3.org/1998/Math/MathML"> i u i_u </math>iu 被穿越前外侧手续费,替换一下即得到公式 (10)。 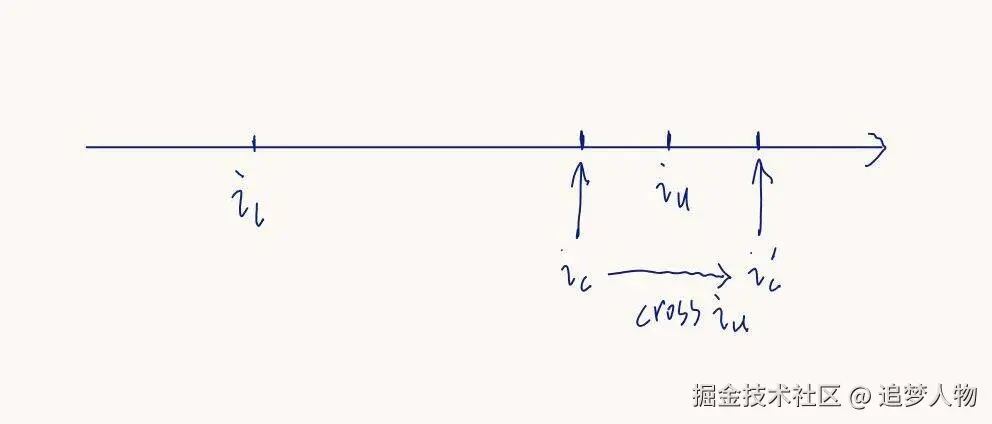 图 3
图 3
知道如何计算某个区间累积的手续费后,在此区间内,按 Position 分配手续费收益即可(其记账方式和 V2 中介绍的直观记账方式一样)。具体来说,一个 LP 如果要撤走其流动性,那么其可分配到的手续费收益计算过程如下:
- 按照上面讲过的方式,计算 Position 区间 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( i l , i u ) (i_l, i_u) </math>(il,iu) 总累积的手续费 <math xmlns="http://www.w3.org/1998/Math/MathML"> f f </math>f(注意是每单位流动性)
- 假设该 Position 流动性为 <math xmlns="http://www.w3.org/1998/Math/MathML"> L L </math>L,上一次提取收益时每单位流动性收益是 <math xmlns="http://www.w3.org/1998/Math/MathML"> f 0 f_0 </math>f0,则本次可分配到的手续费收益总量为 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( f − f 0 ) ⋅ L (f-f_0)\cdot L </math>(f−f0)⋅L
协议费的记账相比手续费简单很多,池子会维护一个总的协议费变量 protocolFee,每一笔交易会计算应当收取的协议费 protocalFeeAmount,然后更新总的协议费 protocolFee += protocalFeeAmount。可以看到,和 Uniswap V2 相比,V3 的协议费在每笔交易中计算,虽然记账方式简单了很多,但需要消耗更多的 gas。