目录
[3.7、 获取队列中中有效元素的个数](#3.7、 获取队列中中有效元素的个数)
一、引言
在计算机科学的浩瀚宇宙中,数据结构如同星辰般构建着算法的运行轨迹。当我们探讨"先进先出"(FIFO)这一朴素而强大的哲学理念时,队列(Queue) 便以秩序维护者的姿态悄然登场。从操作系统调度任务,到网络数据包的有序传输;从打印机作业排队,到游戏中的事件处理------队列无时无刻不在幕后维系着数字世界的运转秩序。
本文将以C语言为刻刀,带您亲手雕琢队列的实现细节:从基础概念到环形缓冲区的精妙设计,从内存管理到多线程环境下的安全挑战。我们不仅会构建一个高性能的动态队列,更将深入剖析其底层原理,揭示数据流转的艺术。无论您是初探数据结构的新手,还是寻求性能优化的资深开发者,这场与队列的深度对话都将为您打开新的思考维度。
二、队列的基本概念
2.1、队列的定义
队列:只允许在一端进行插入操作,在另一端进行删除操作的特殊线性表。其特点与栈相反,为先进先出。
2.2、物理结构的选择
实现队列结构,用顺序表好呢,还是链表好呢?队列涉及两头操作问题,如果选择顺序表,必然会因为数据的删除或者插入引起整个数组的平移,耗费时间,如果每次不平移,就会导致假溢出,浪费空间。所以我们选择链式结构,并特定标明链表头和链表尾
三、C语言动态实现队列
3.1、队列结构的定义
既然选择链表实现队列,首先就要构造链表结构,这里选择单链表。
cpp
//定义链表结构
typedef int QueueDataType;
typedef struct QueueNode
{
QueueDataType data;
struct QueueNode* next;
}QueueNode;然后才是队列结构
cpp
//定义队列结构
typedef struct Queue
{
QueueNode* phead; //队头
QueueNode* ptail; //对尾
}Queue;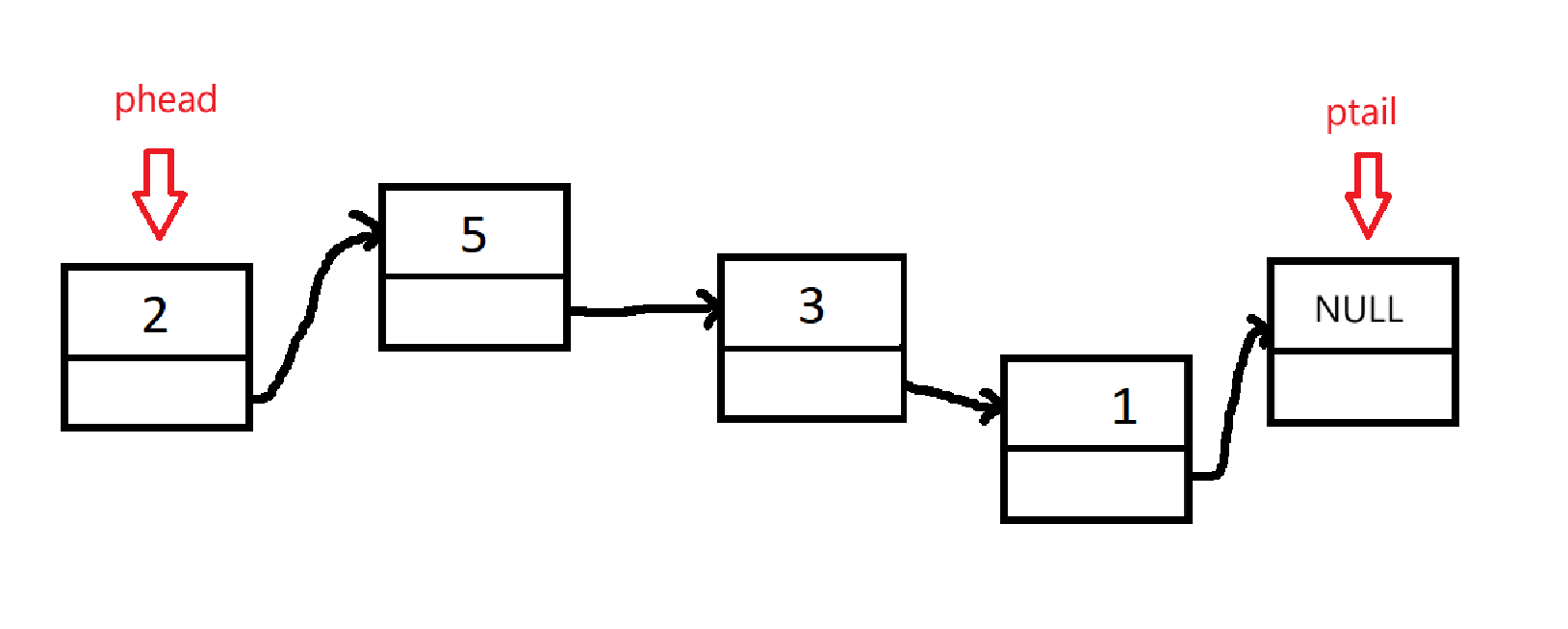
3.2、初始化
队列初始化很简单,把它的两个指针成员置为 NULL 就可以了。
cpp
void QueueInit(Queue* q)
{
assert(q);
q->phead = q->ptail = NULL;
}3.3、入队
由于初始化没有创建链表,所以在入队的时候需要先判断是否要创建链表。然后在进行入队操作。
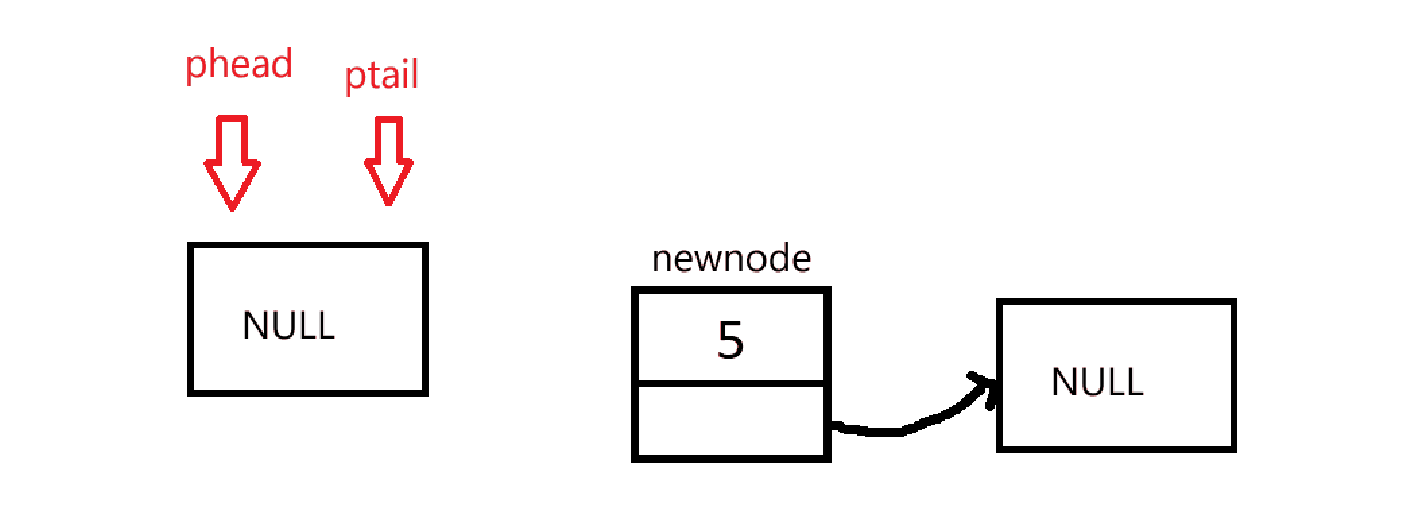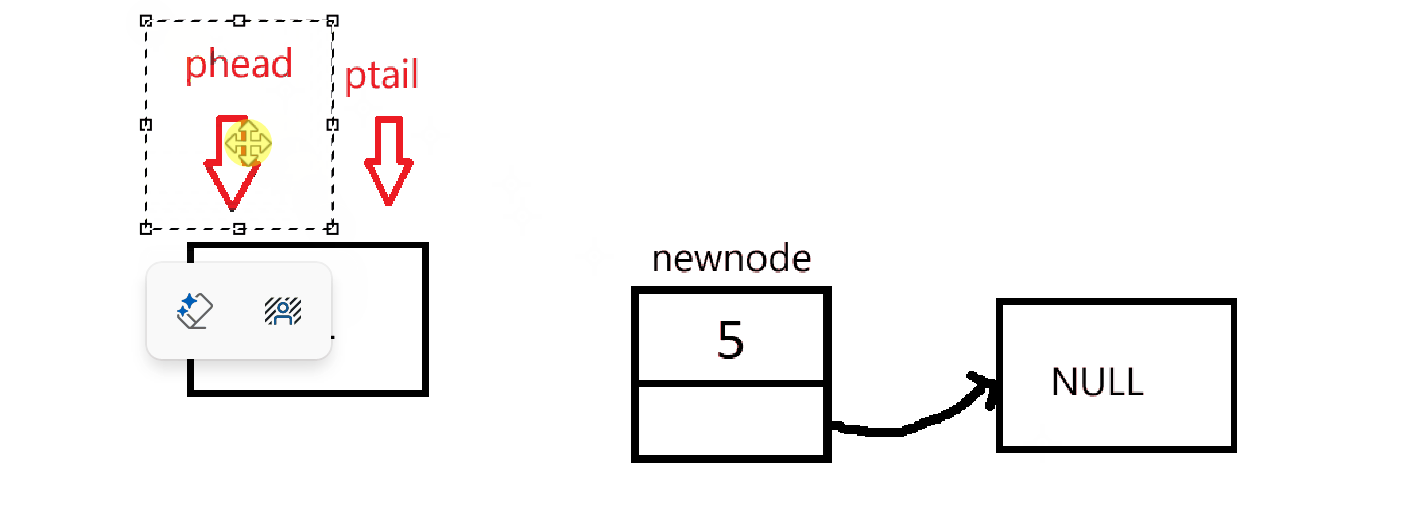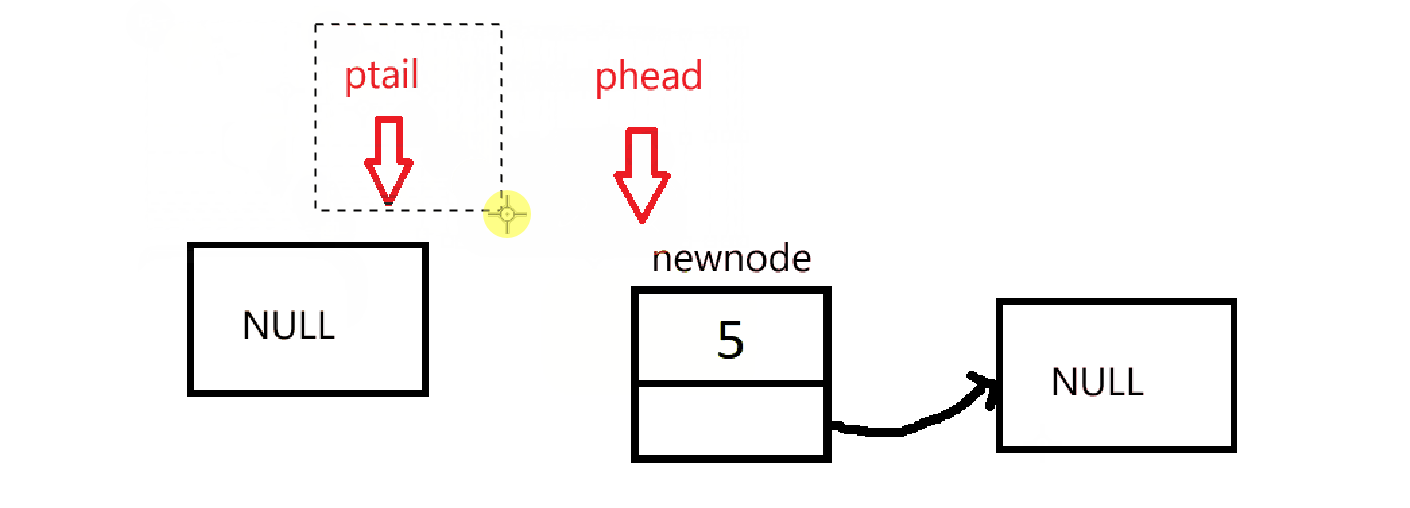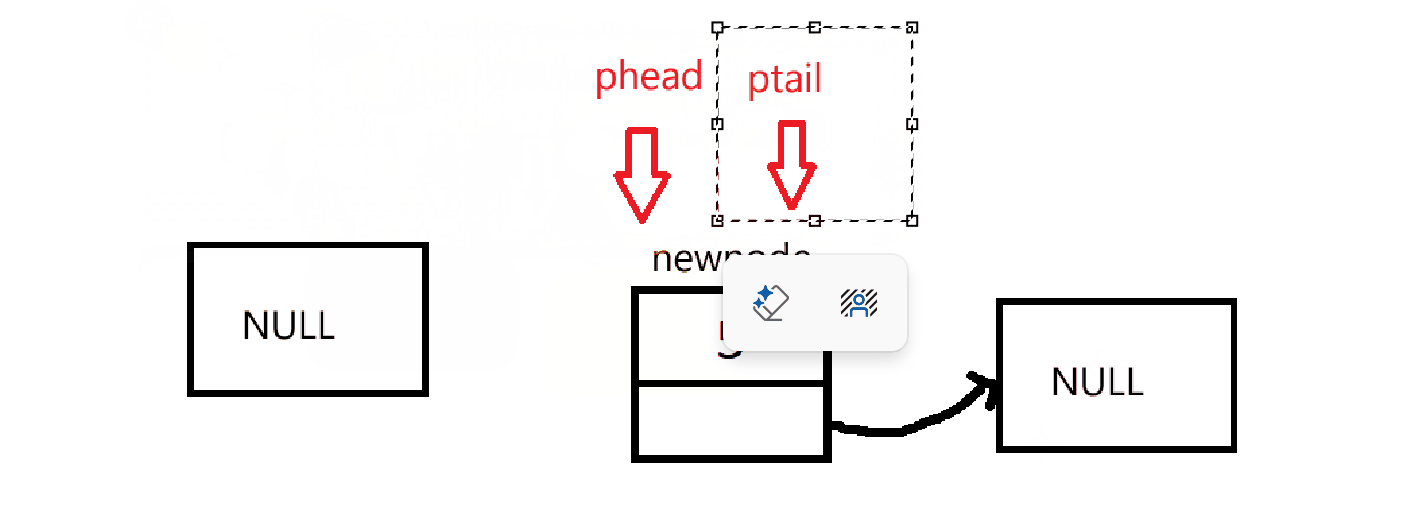
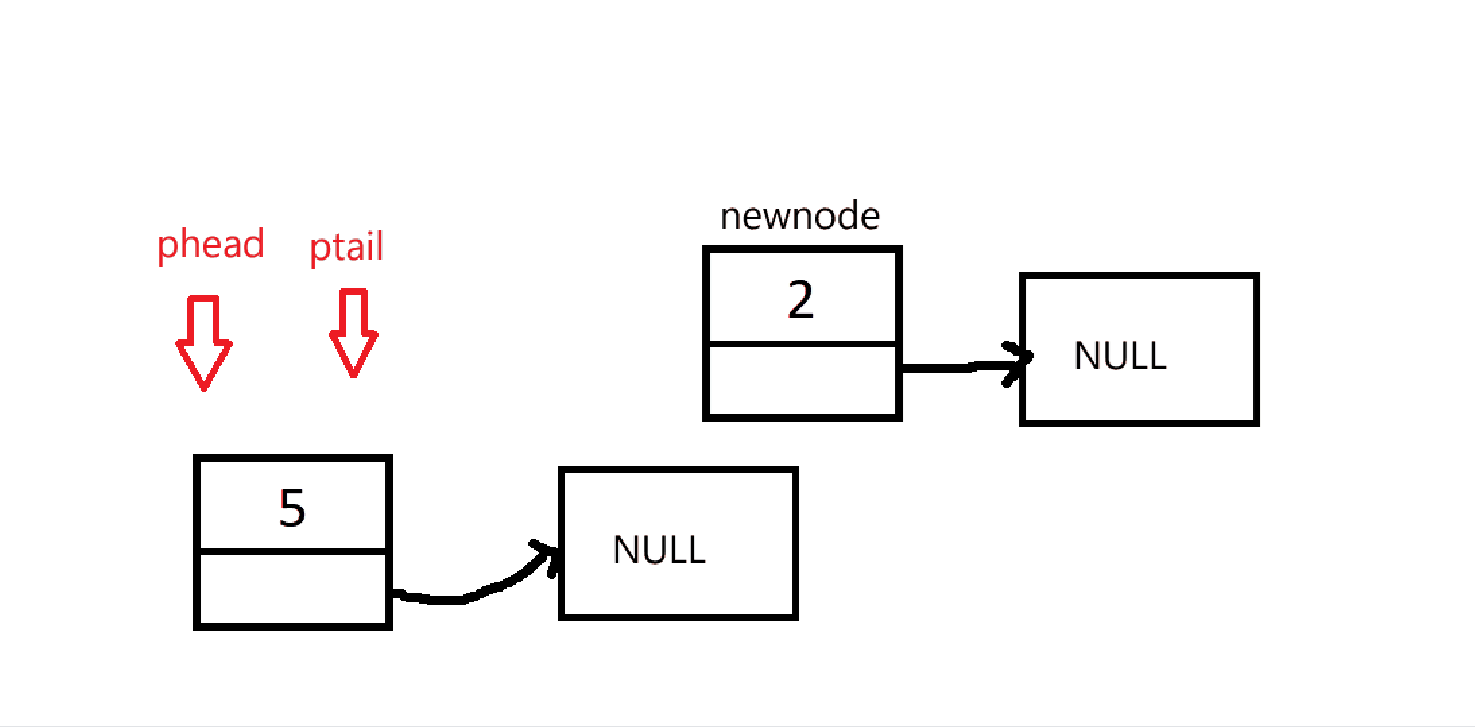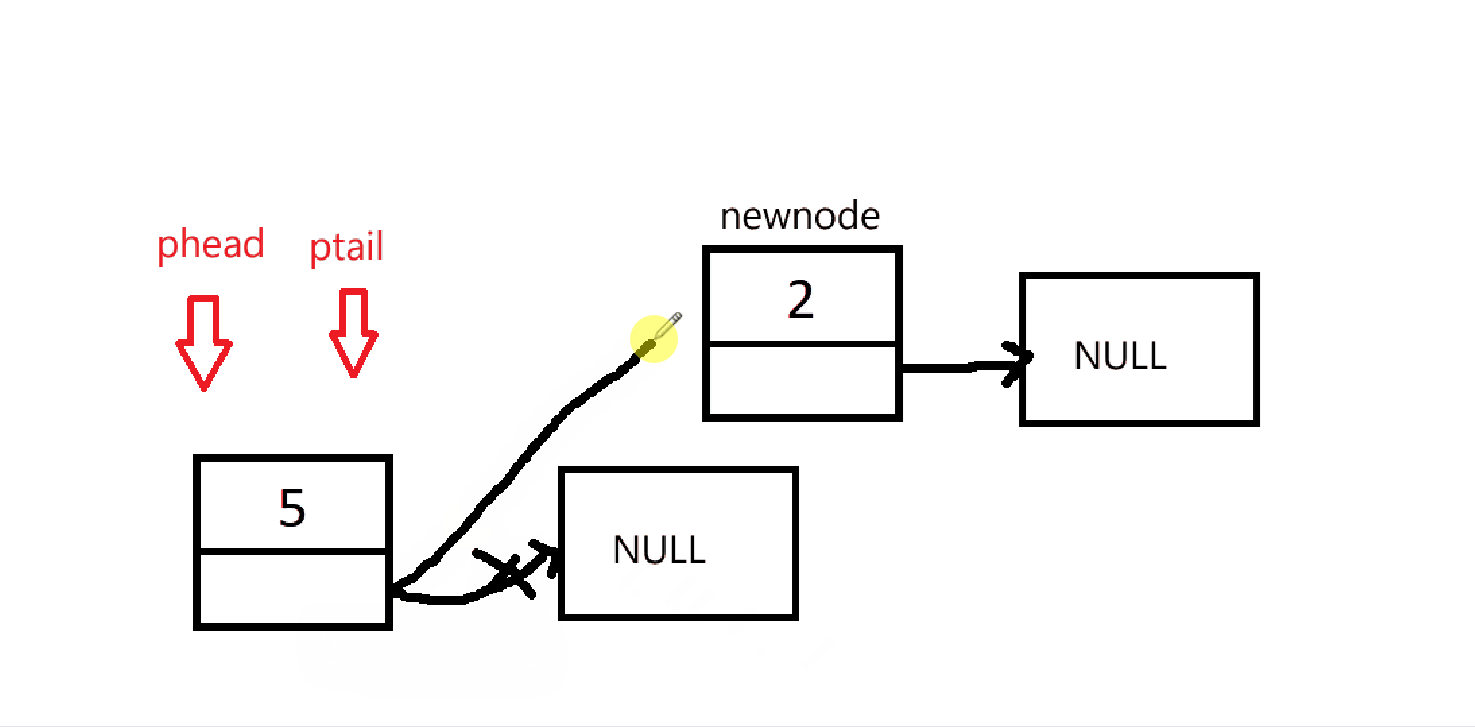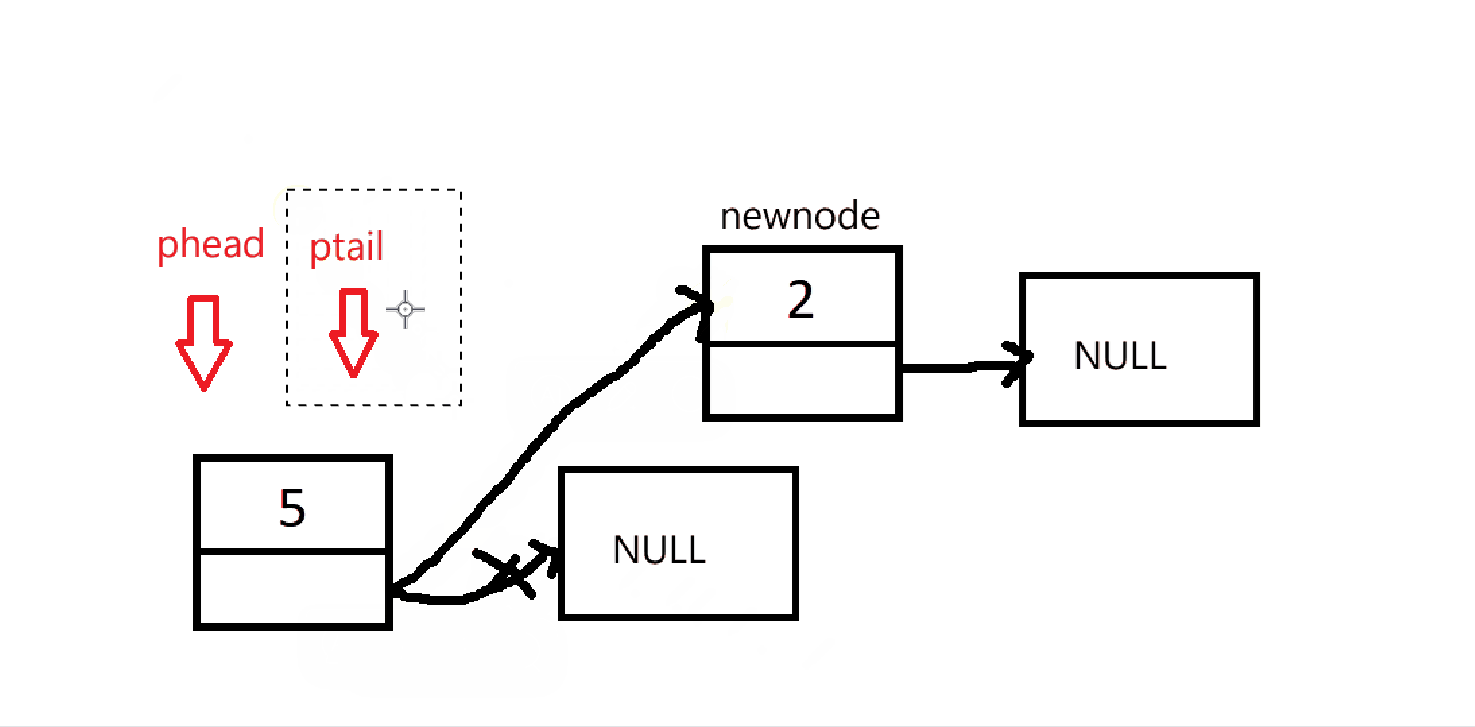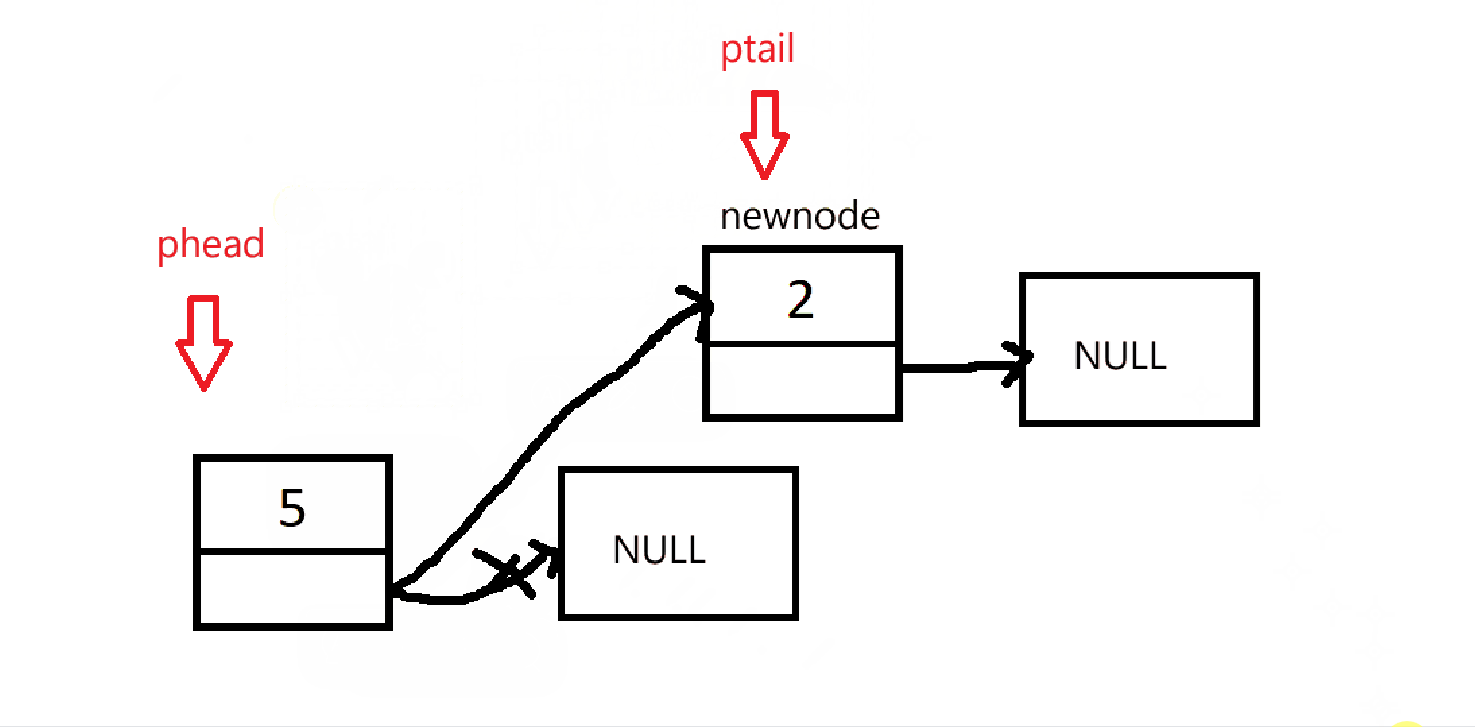
cpp
void QueuePush(Queue* q, QueueDataType x)
{
assert(q);
//创建新节点
QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
if (newnode == NULL)
{
perror("malloc fail!");
exit(1);
}
newnode->data = x;
newnode->next = NULL;
//判断需不需要建立链表
if (q->phead == NULL)
{
q->phead = q->ptail = newnode;
}
else
{
q->ptail->next = newnode;
q->ptail = newnode;
}
}3.4、判断队列是否为空
判断队列是否为空,只需要看队列的成员phead是否指向NULL
cpp
bool QueueEmpty(Queue* q)
{
assert(q);
return q->phead == NULL;
}3.5、出队
出队和单链表删除节点是一样的,只不过队列只能删除队头而已。不要忘记检查队列是否为空!
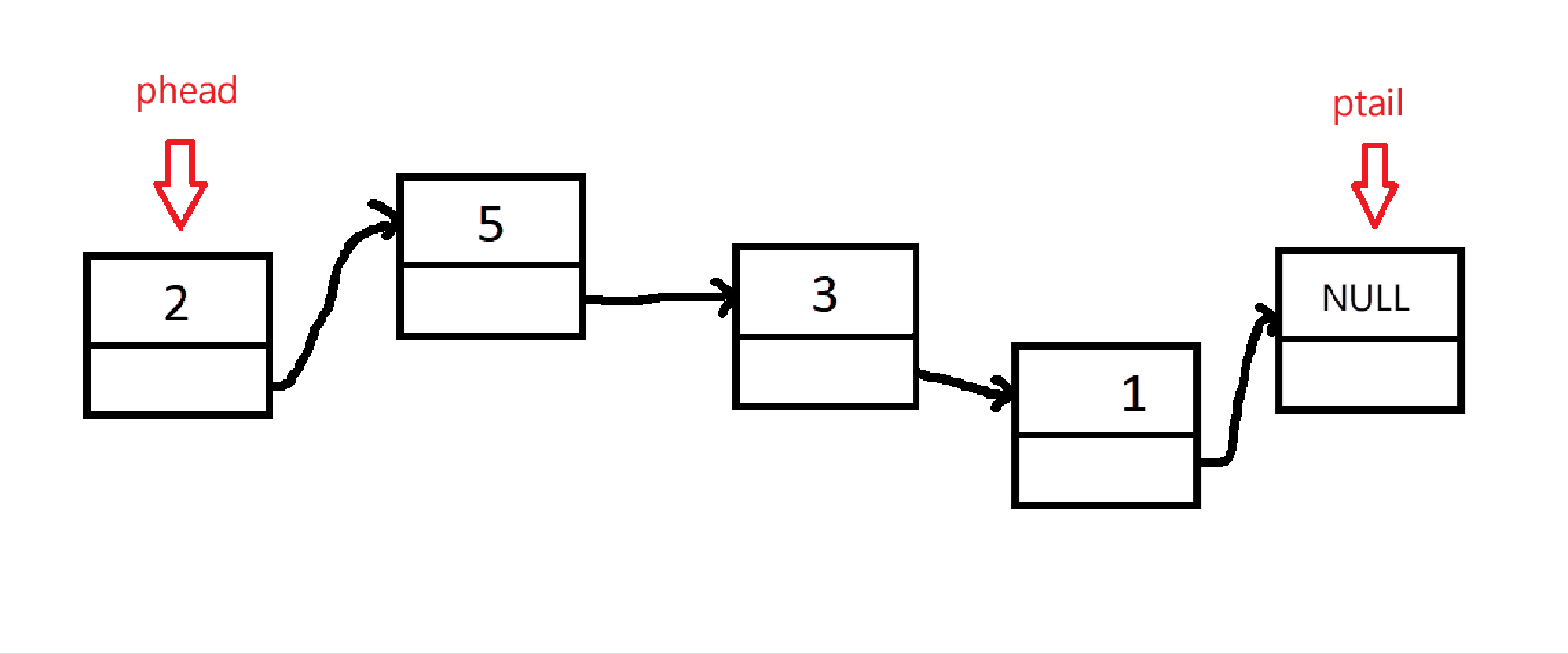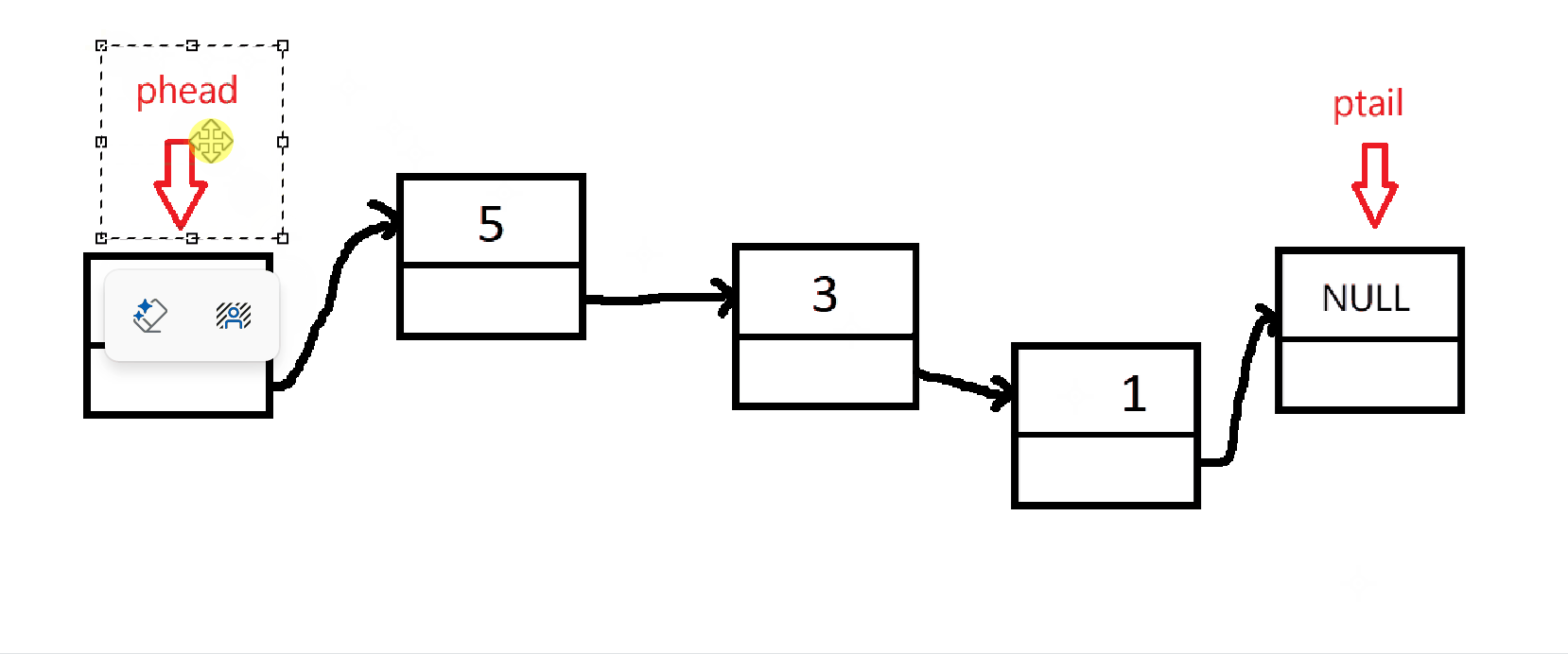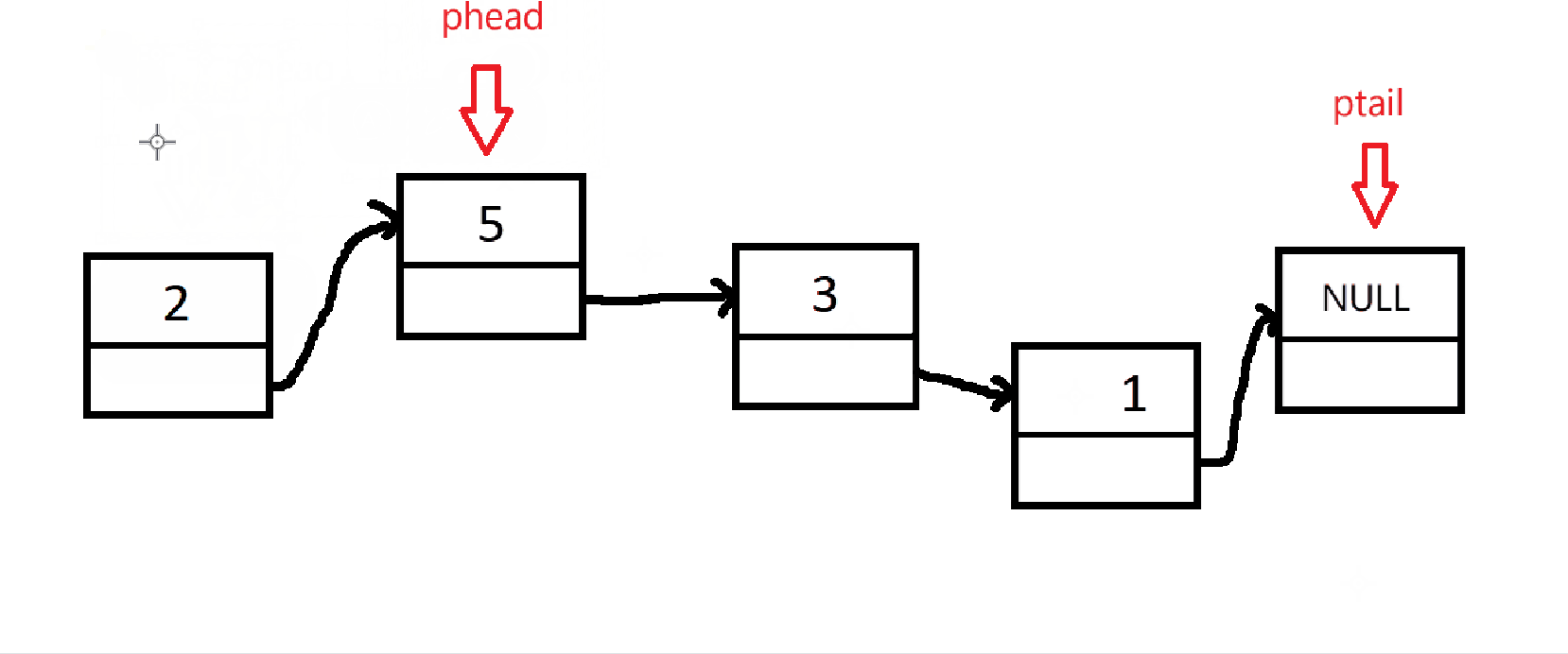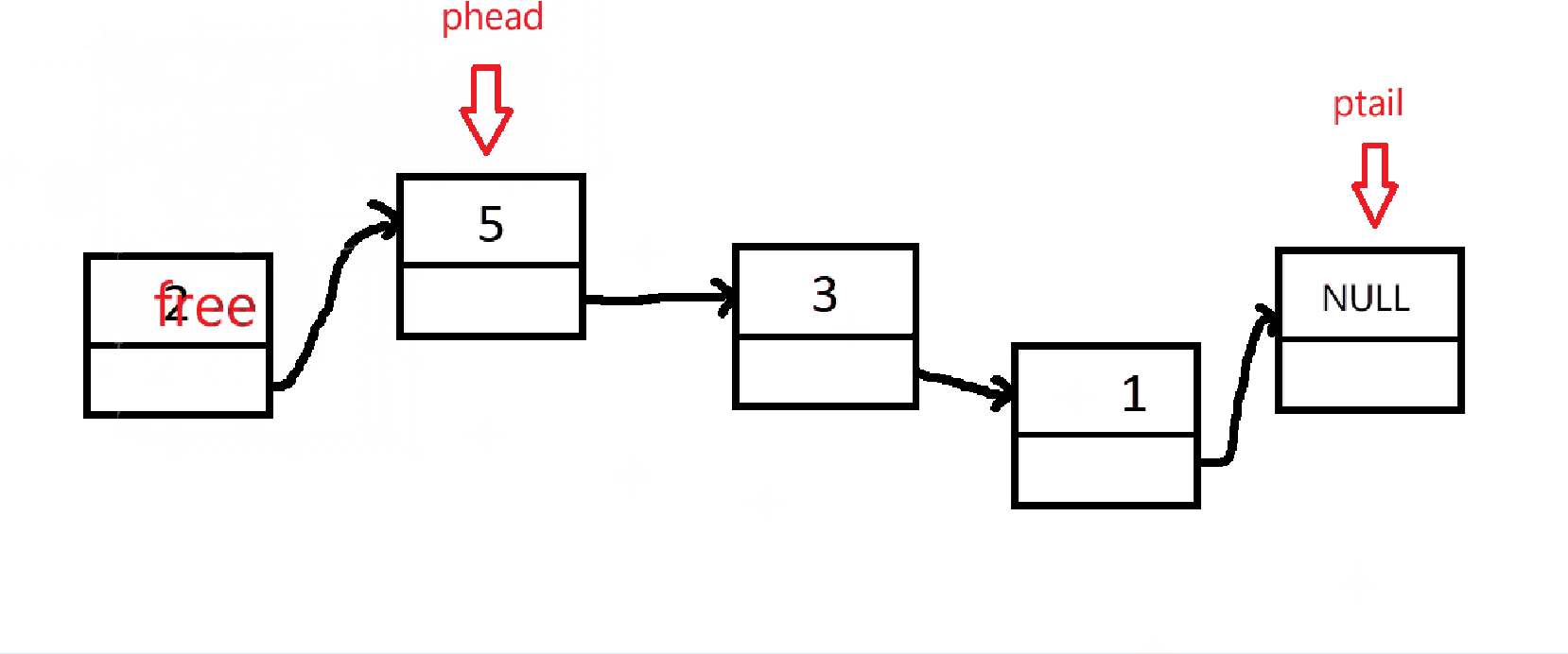
但是,如果只有一个节点,被删除后,队列的头尾指针应该都指向NULL
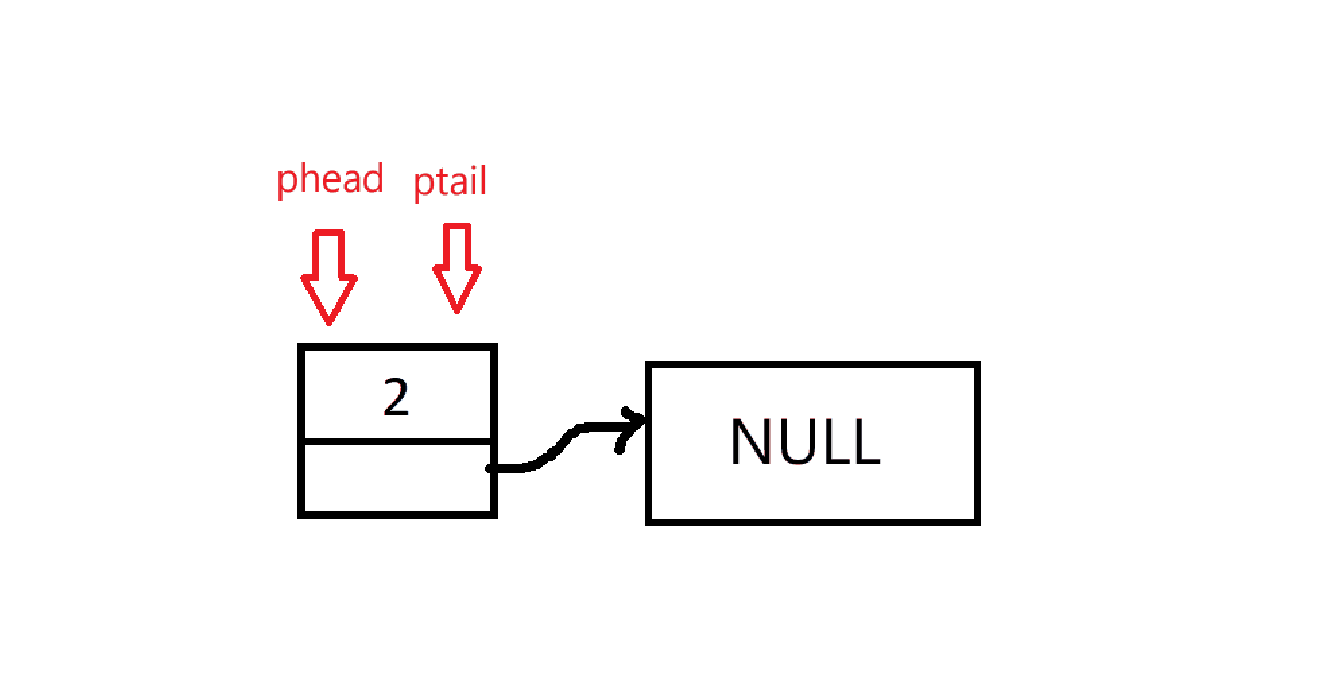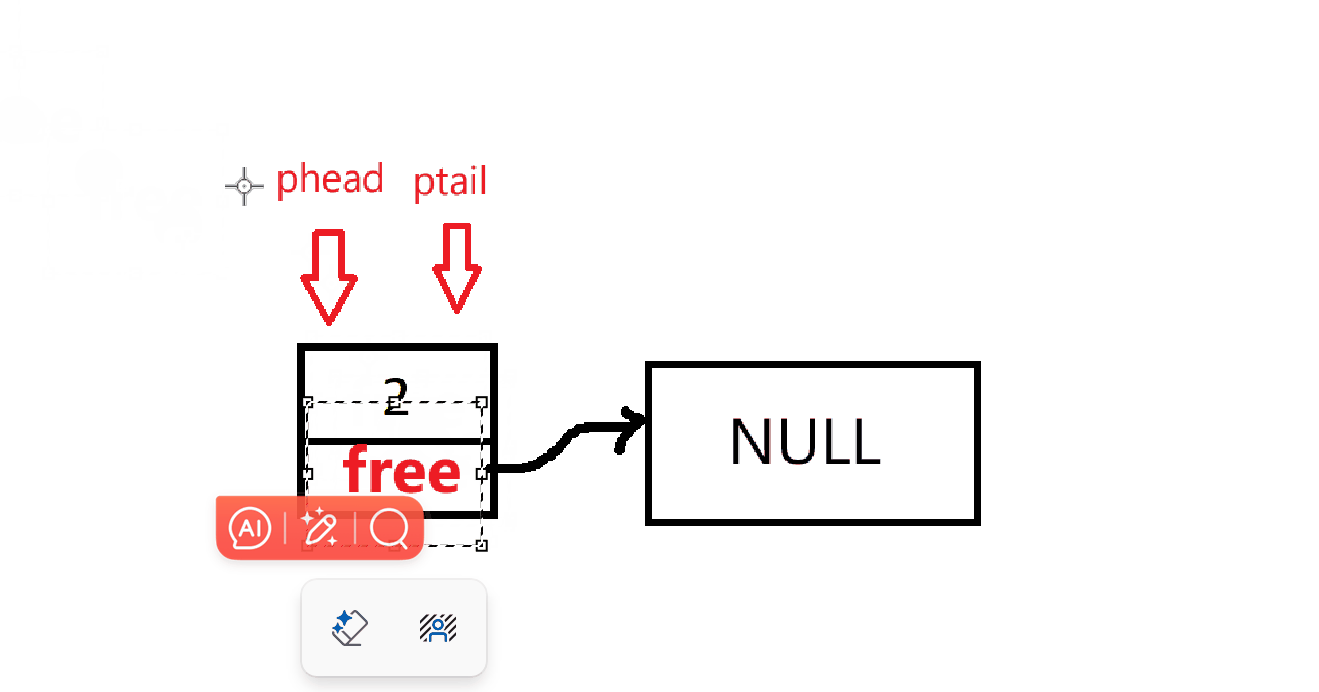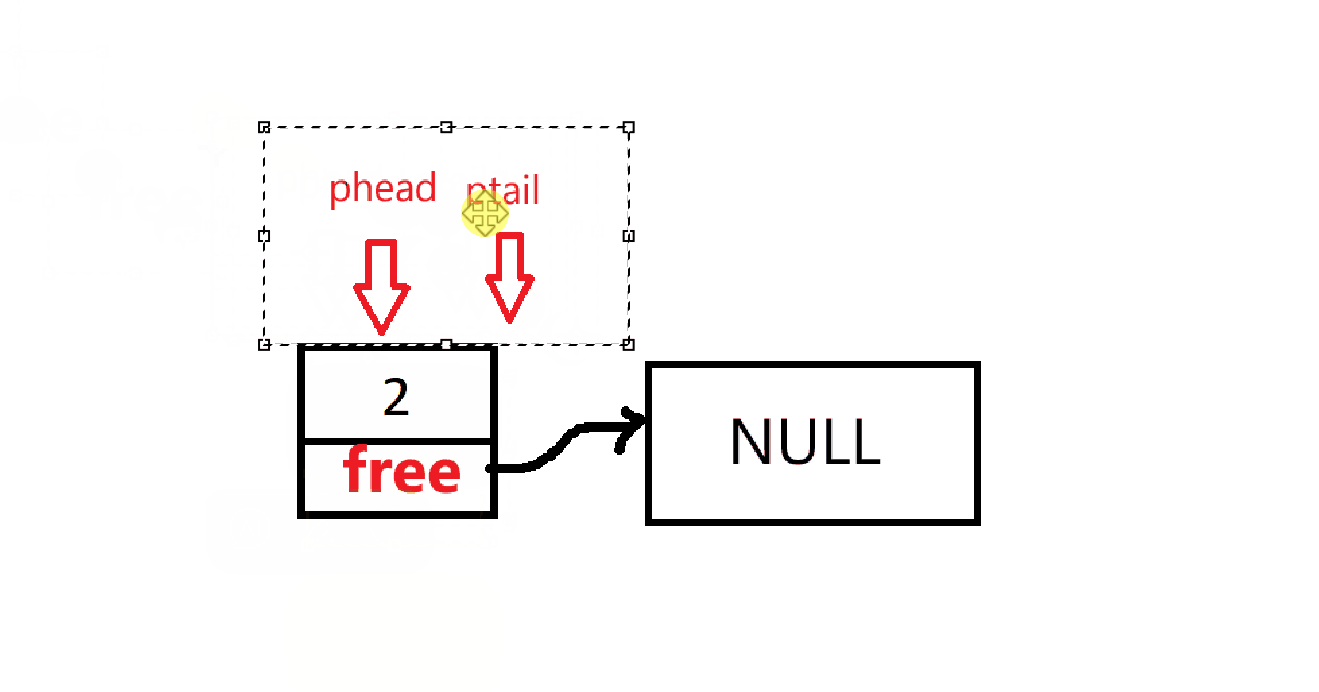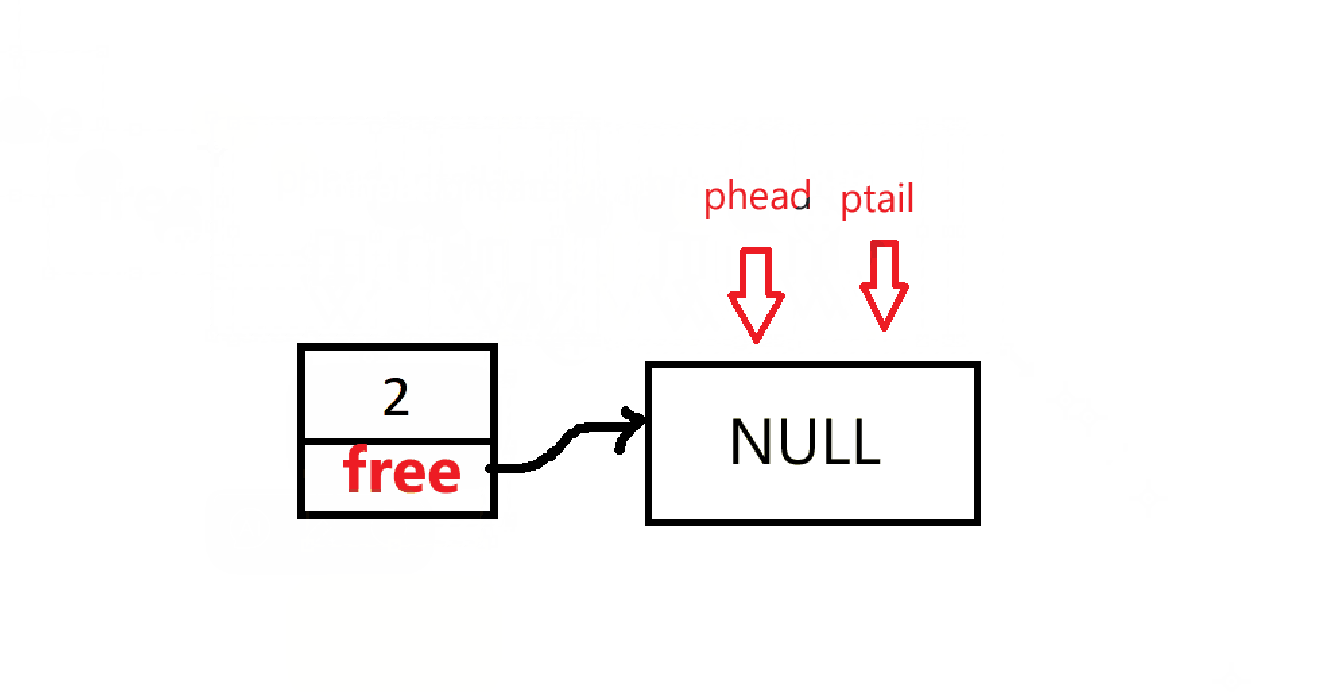
代码如下:
cpp
void QueuePop(Queue* q)
{
assert(!QueueEmpty(q));
//判断是否只剩一个节点
if (q->phead == q->ptail)
{
free(q->phead);
q->phead = q->ptail = NULL;
}
else
{
QueueNode* tmd = q->phead->next;
free(q->phead);
q->phead = tmd;
}
}3.6、取队头数据
这个直接返回队头数据,没什么好说的了
cpp
QueueDataType QueueTop(Queue* q)
{
assert(!QueueEmpty(q));
return q->phead->data;
}3.7、 获取队列中中有效元素的个数
创建一个变量,然后依次遍历整个队列链表
cpp
int QueueSize(Queue* q)
{
assert(q);
QueueNode* pcur = q->phead;
int count = 0;
while (pcur != NULL)
{
count++;
pcur = pcur->next;
}
return count;
}或者,在定义队列结构的时候就加上有效元素大小。
3.8、队列的销毁
根单链表的销毁一样,链式销毁
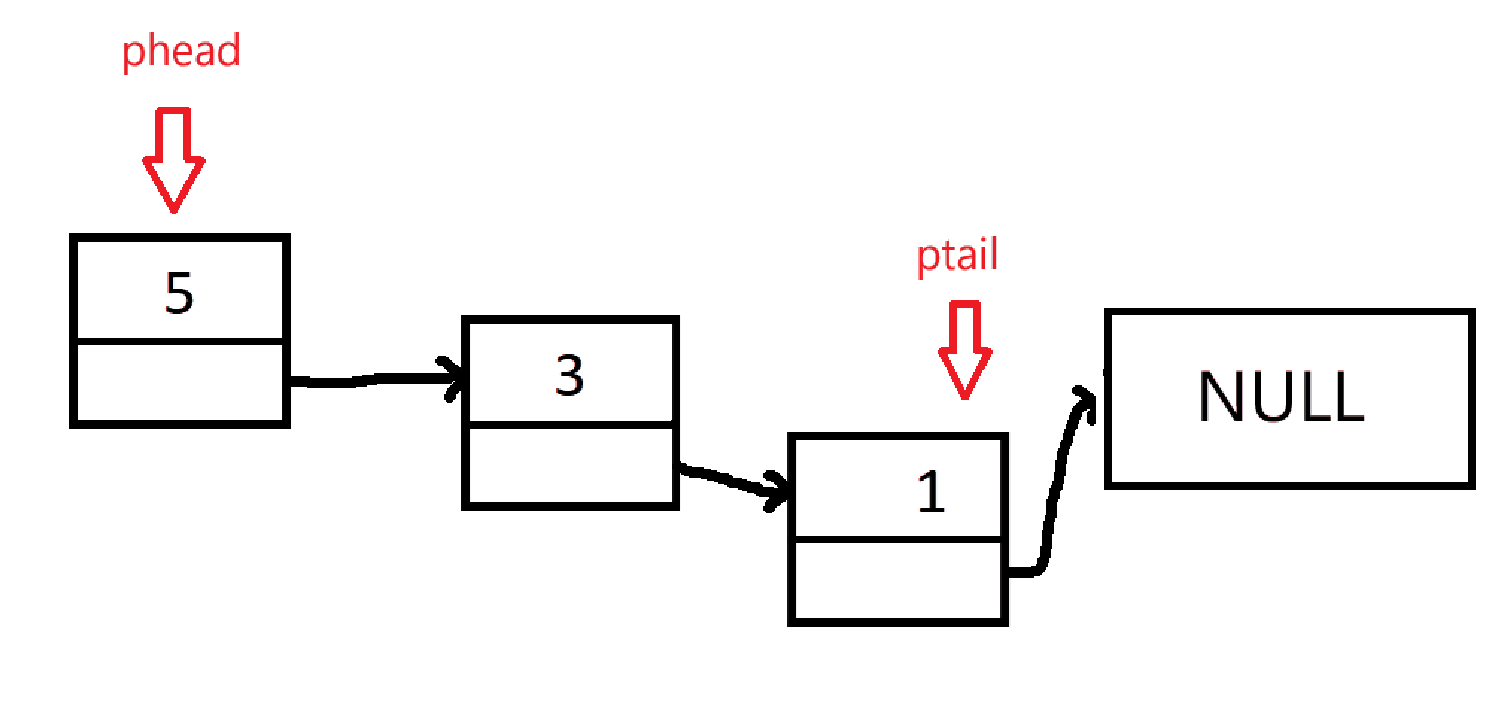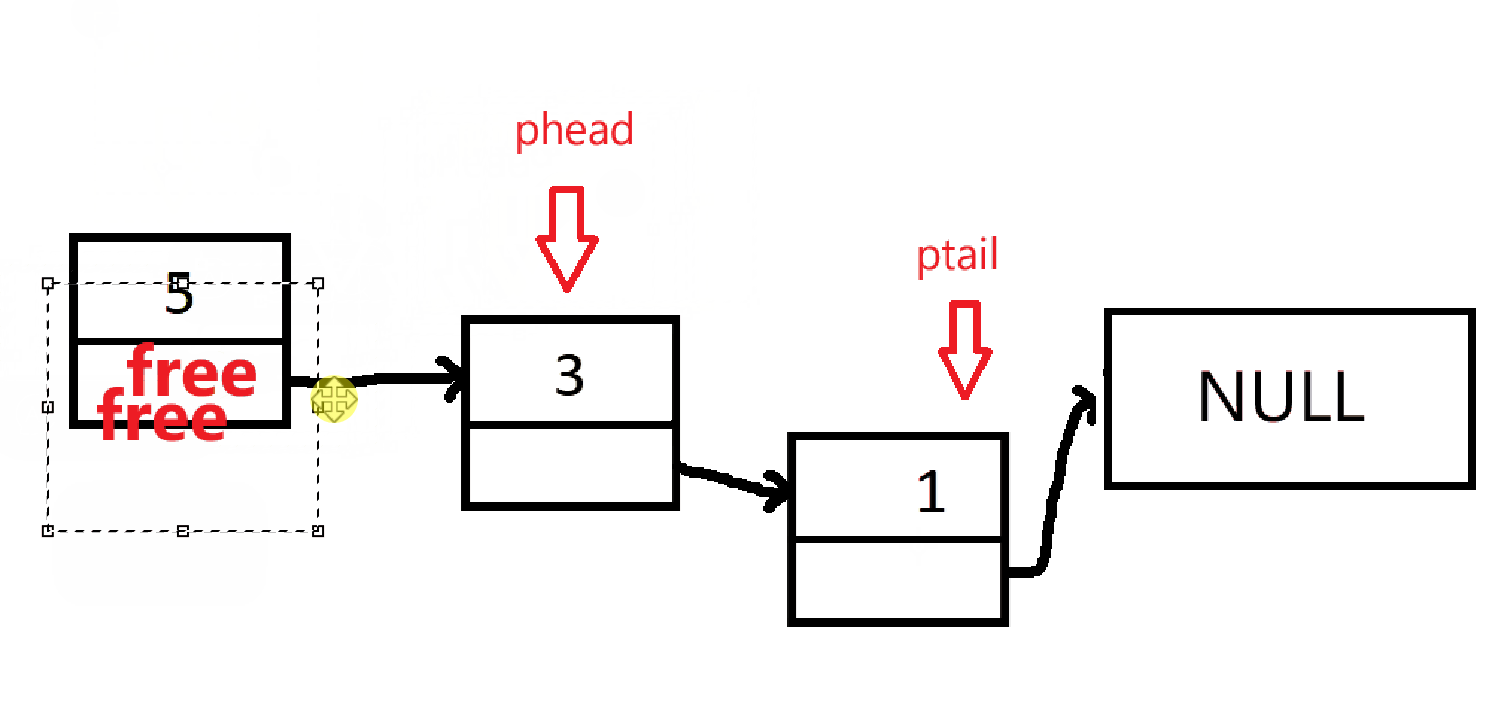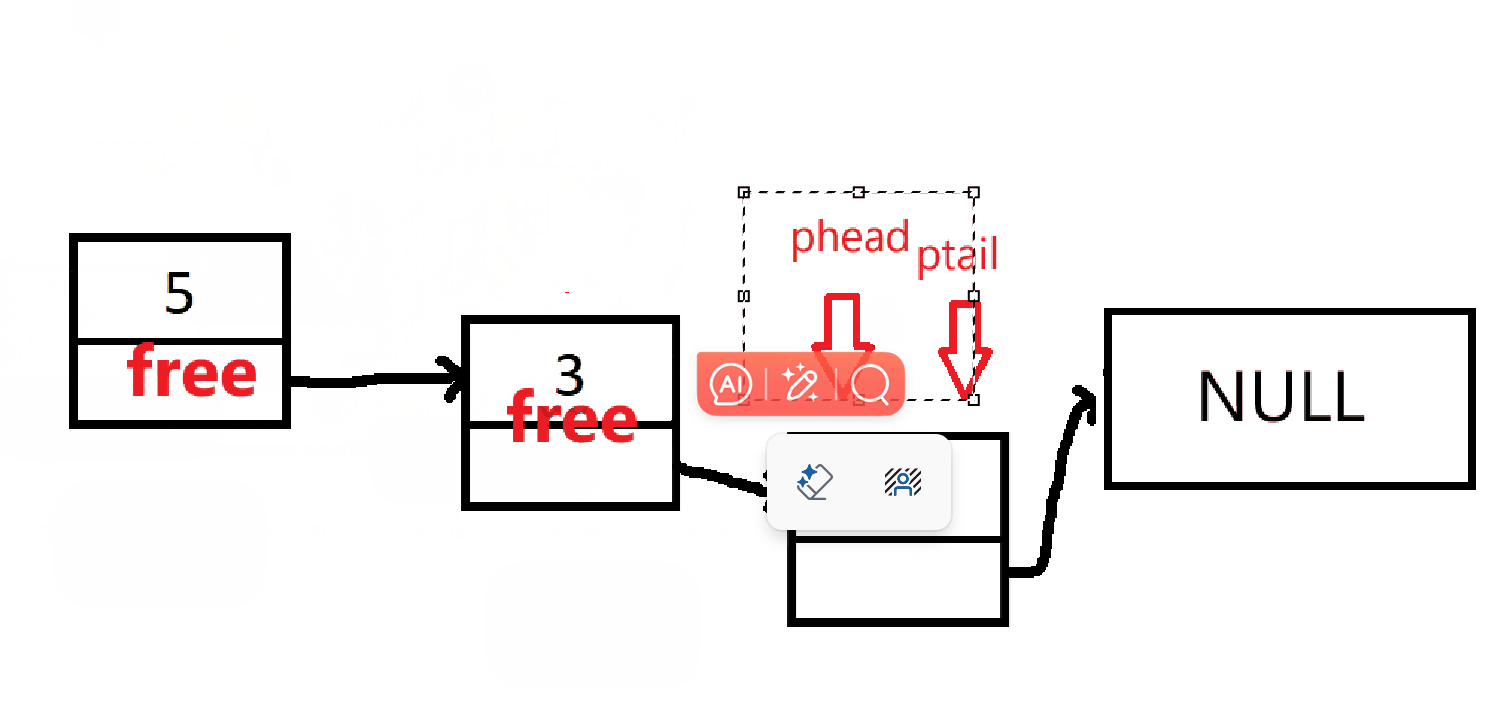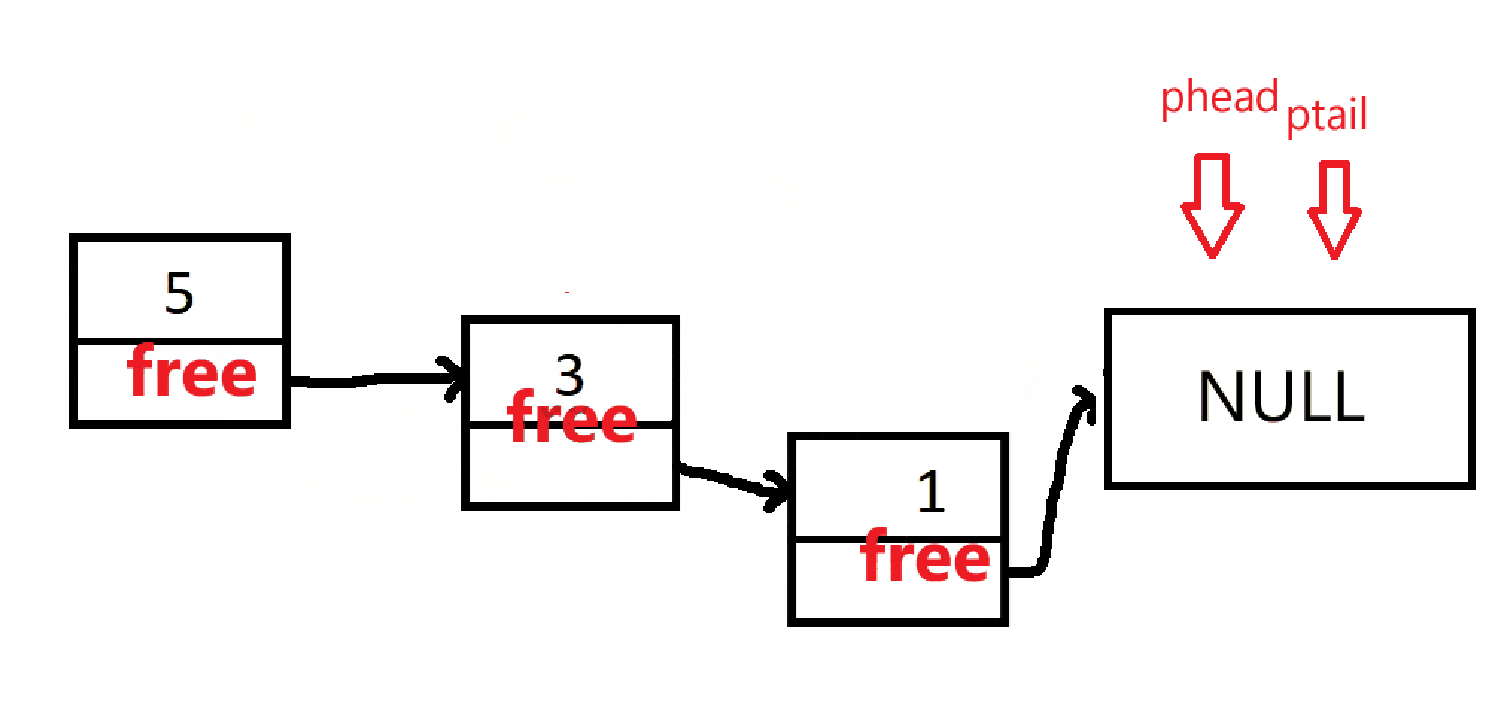
cpp
void QueueDestory(Queue* q)
{
assert(q);
while (q->phead != NULL)
{
QueueNode* next = q->phead->next;
free(q->phead);
q->phead = next;
}
q->phead = q->ptail = NULL;
}四、练习题
4.1、用队列实现栈

题目要求是用两个队列实现一个栈,由先入先出到先入后出,有什么办法呢?
将 n 个数据依次插入队列中,再将前 n-1 个数据放入另一个队列中,则第一个队列出队即可完成先入后出的栈
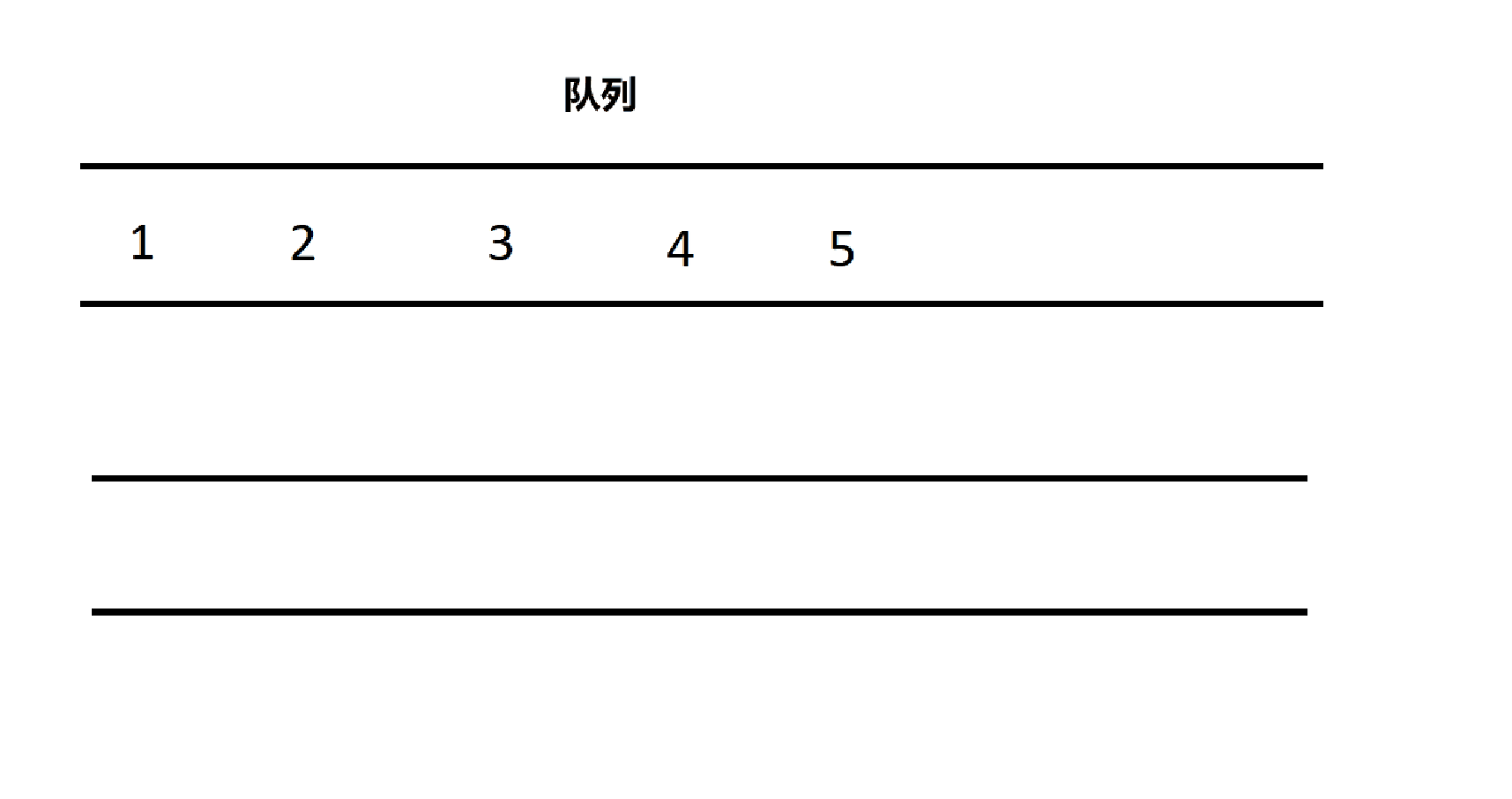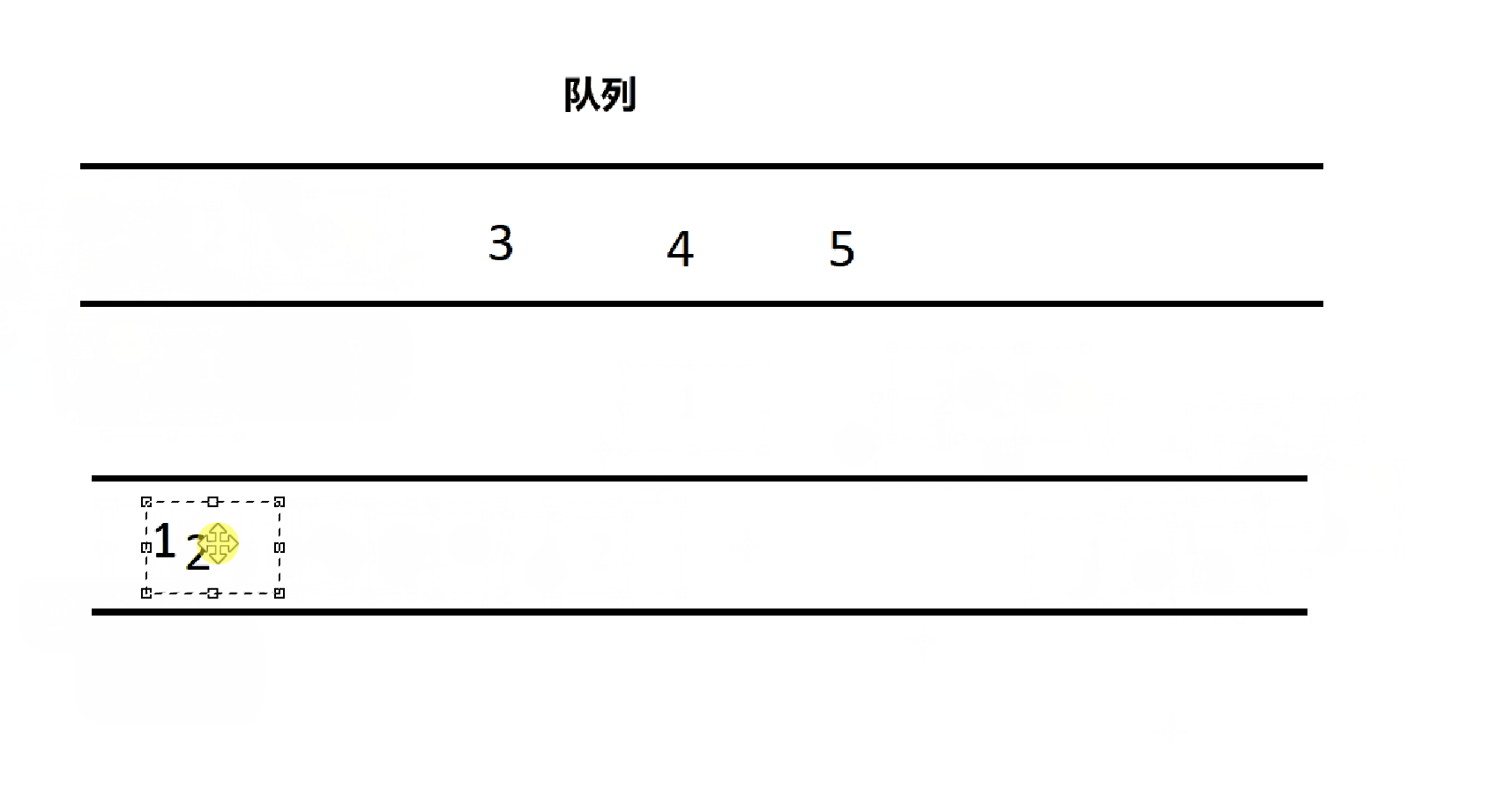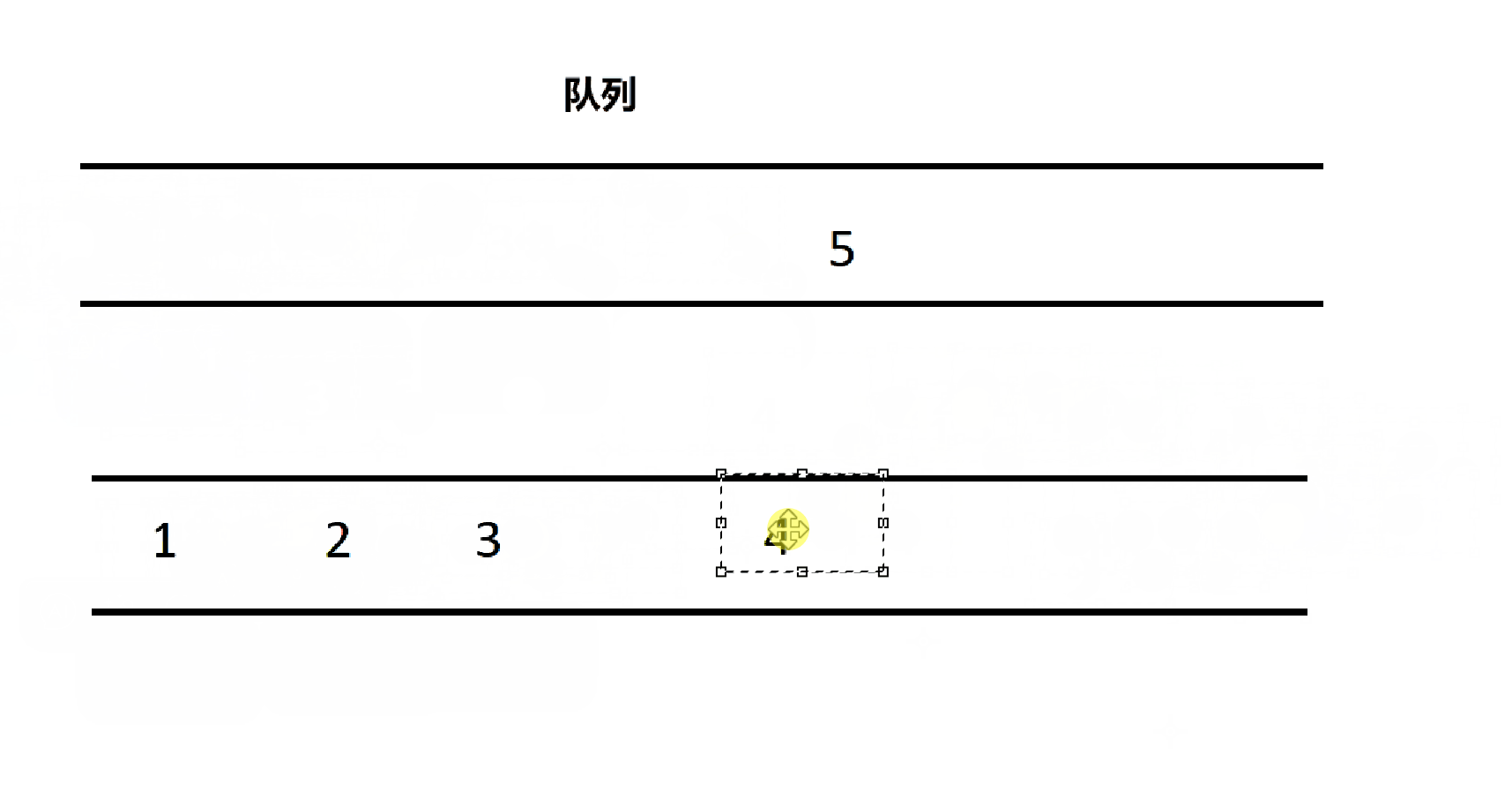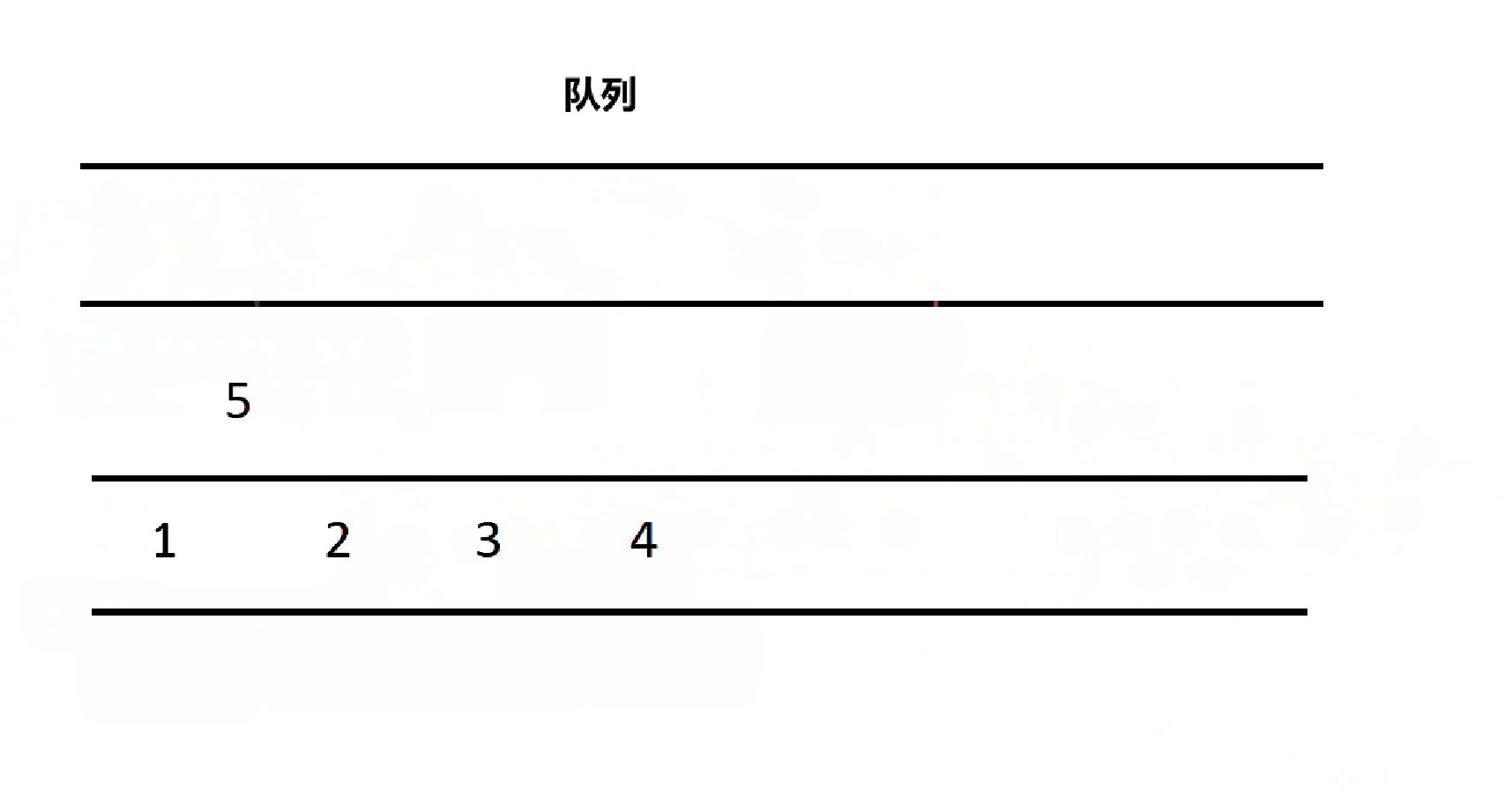
4.1.1、栈的结构
由上面的思路可以知道,栈中有两个队列,因此,定义栈的结构:
cpp
typedef struct MyStack
{
Queue q1;
Queue q2;
}MyStack;补充:这里队列的相关函数和本文上面的一致!
4.1.2、栈的创建
创建一个栈,还要返回,因此不能创建一个变量,因为该变量会在函数结束后销毁,要用malloc申请空间才能长久保存。
cpp
MyStack* myStackCreate() {
//申请一块栈的空间
MyStack* st = (MyStack*)malloc(sizeof(MyStack));
if(st == NULL)
{
perror("malloc fail!");
exit(1);
}
//初始化栈的两个队列
QueueInit(&st->q1);
QueueInit(&st->q2);
return st;
}4.1.3、入栈
根据已经有的思路,我们应该选择一个空的队列插入数据,刚开始两个队列都是空的,随便选个就好了。
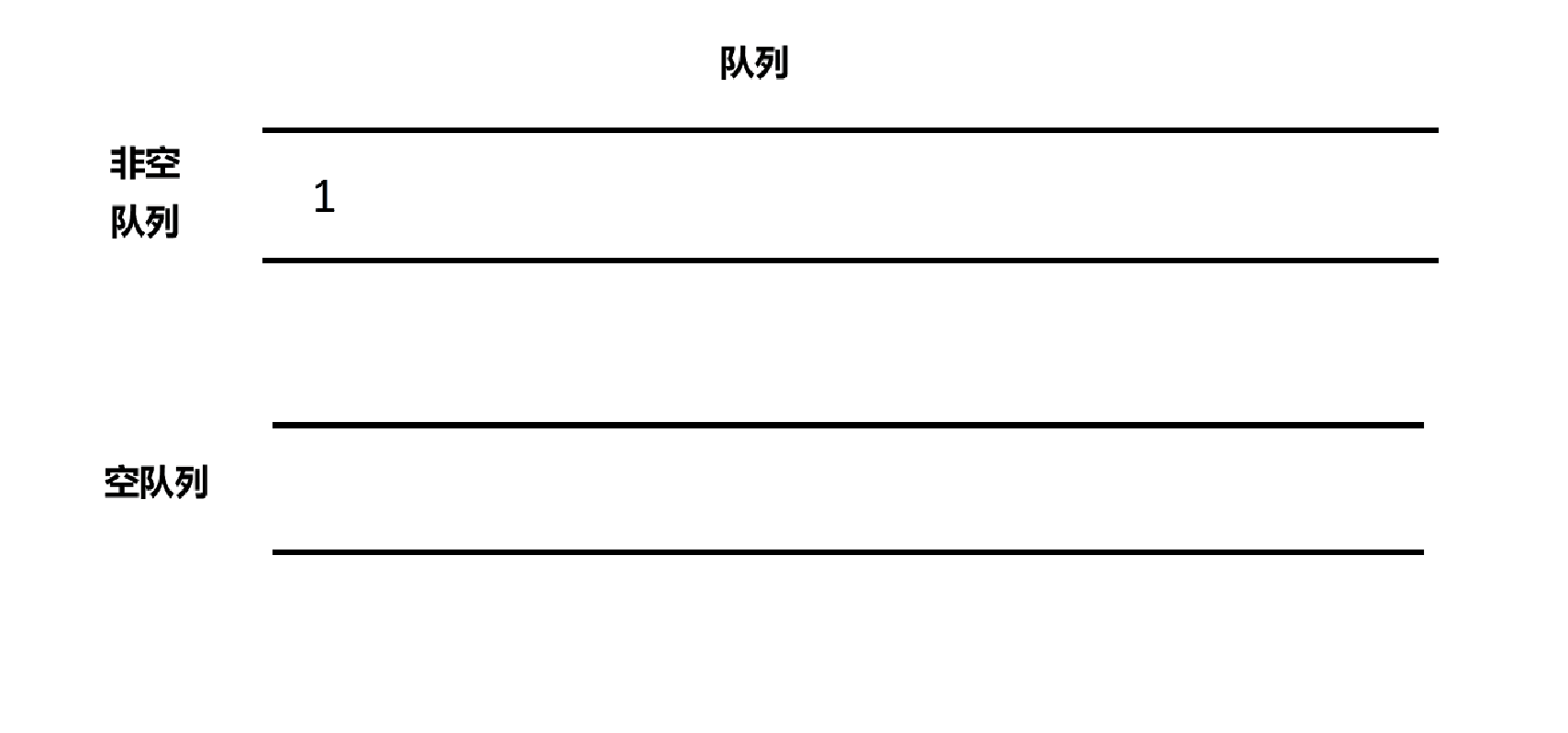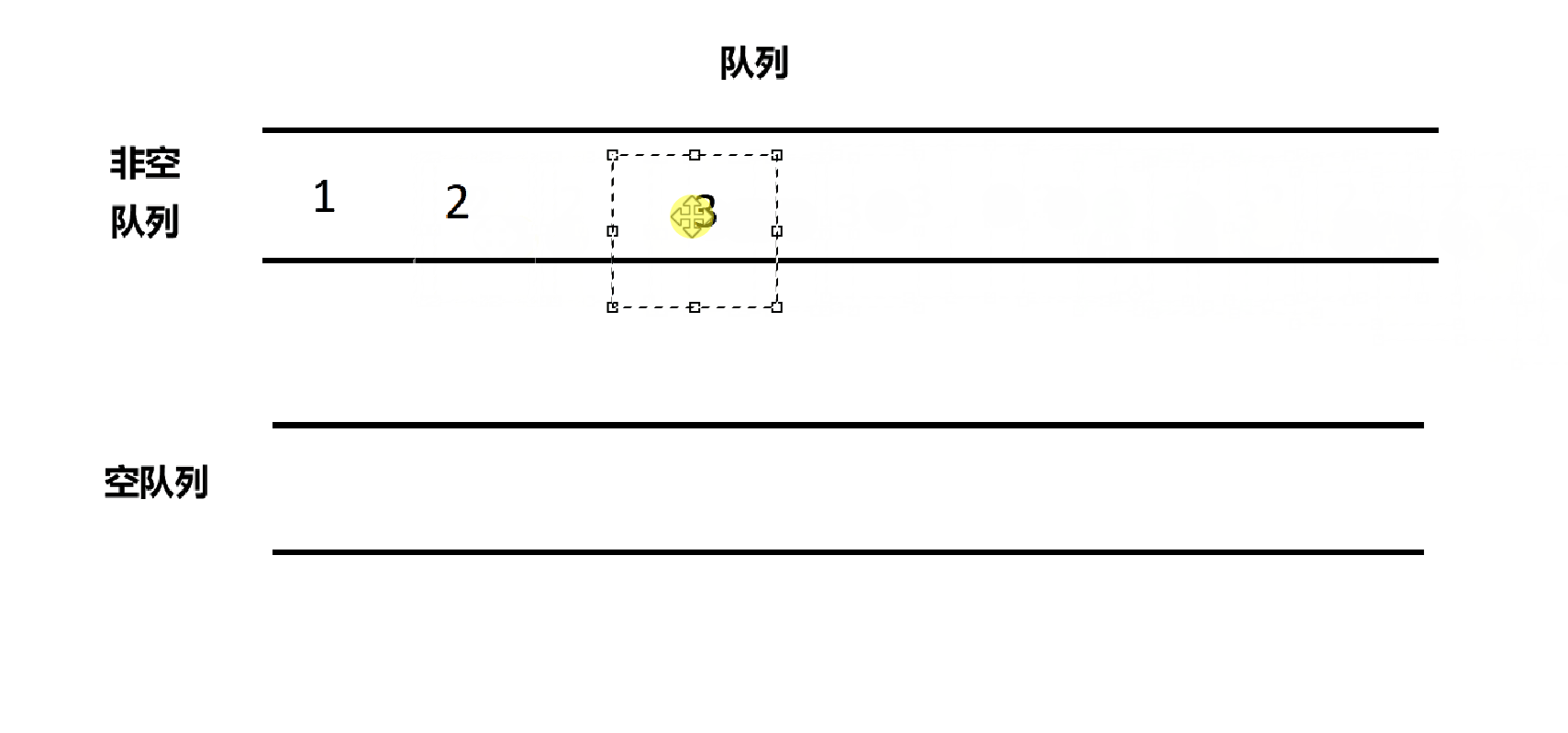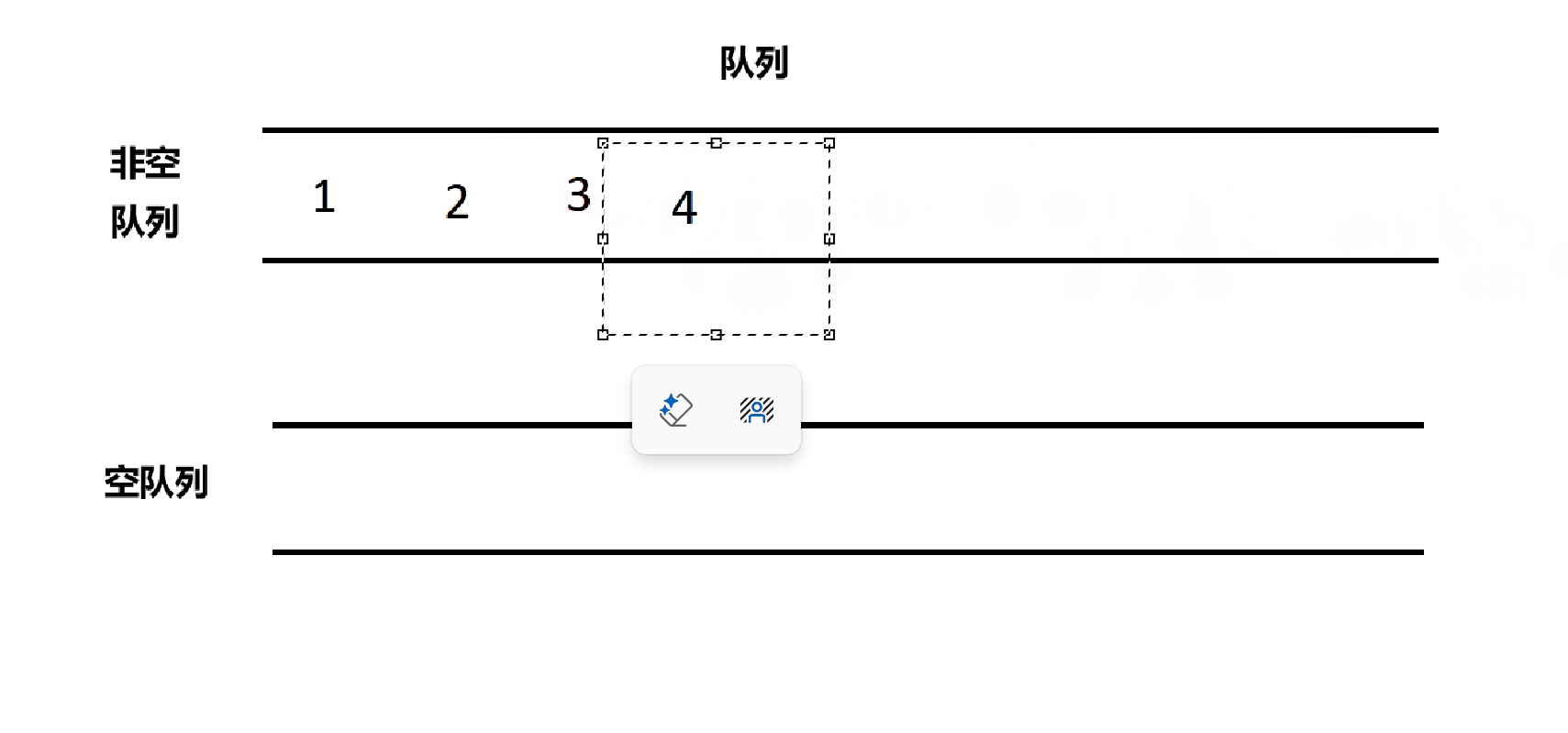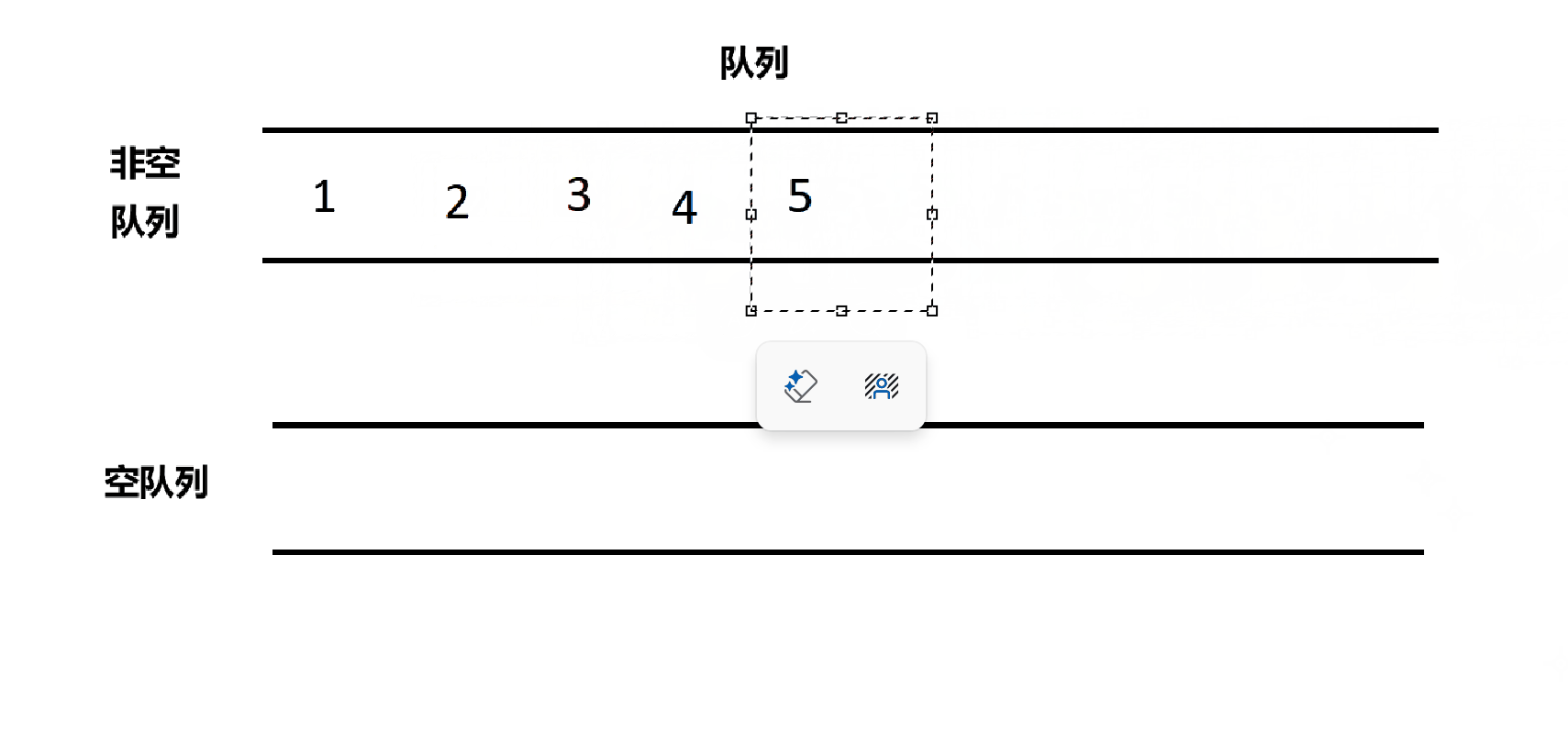
cpp
void myStackPush(MyStack* obj, int x) {
assert(obj);
//判断谁不是空队列
if(!QueueEmpty(&obj->q1))
{
//谁不是空队列就往谁入队
QueuePush(&obj->q1 , x);
}
else
{
QueuePush(&obj->q2 , x);
}
}4.1.4、出栈
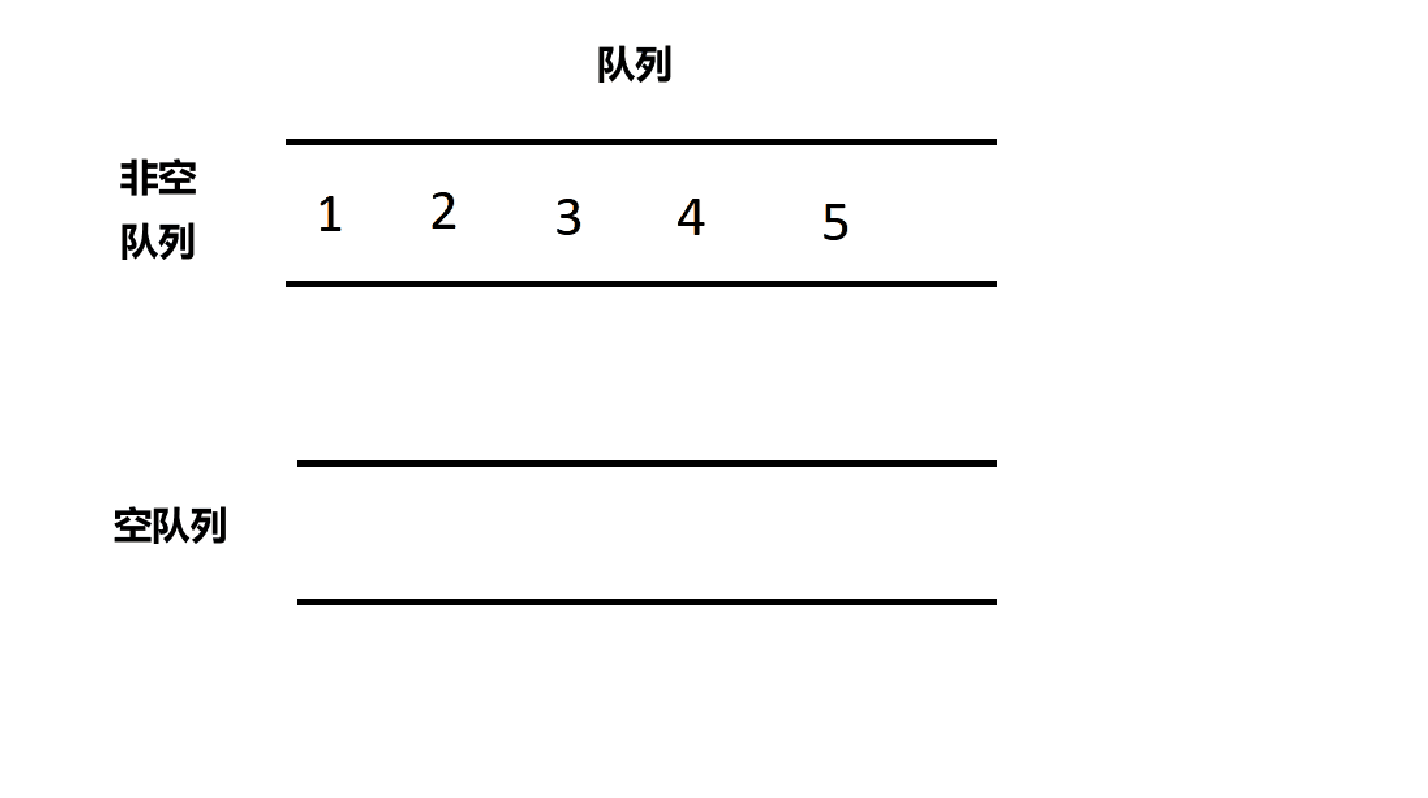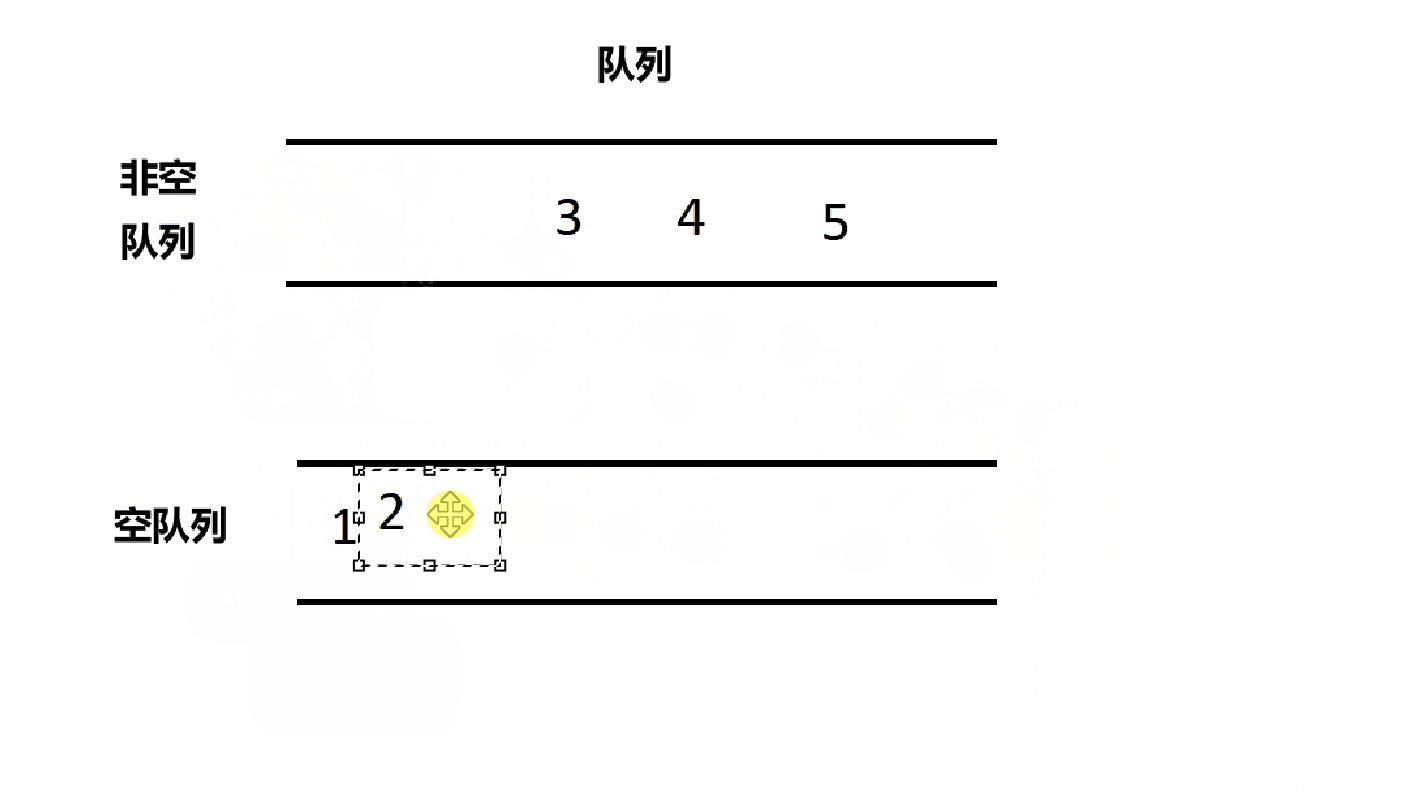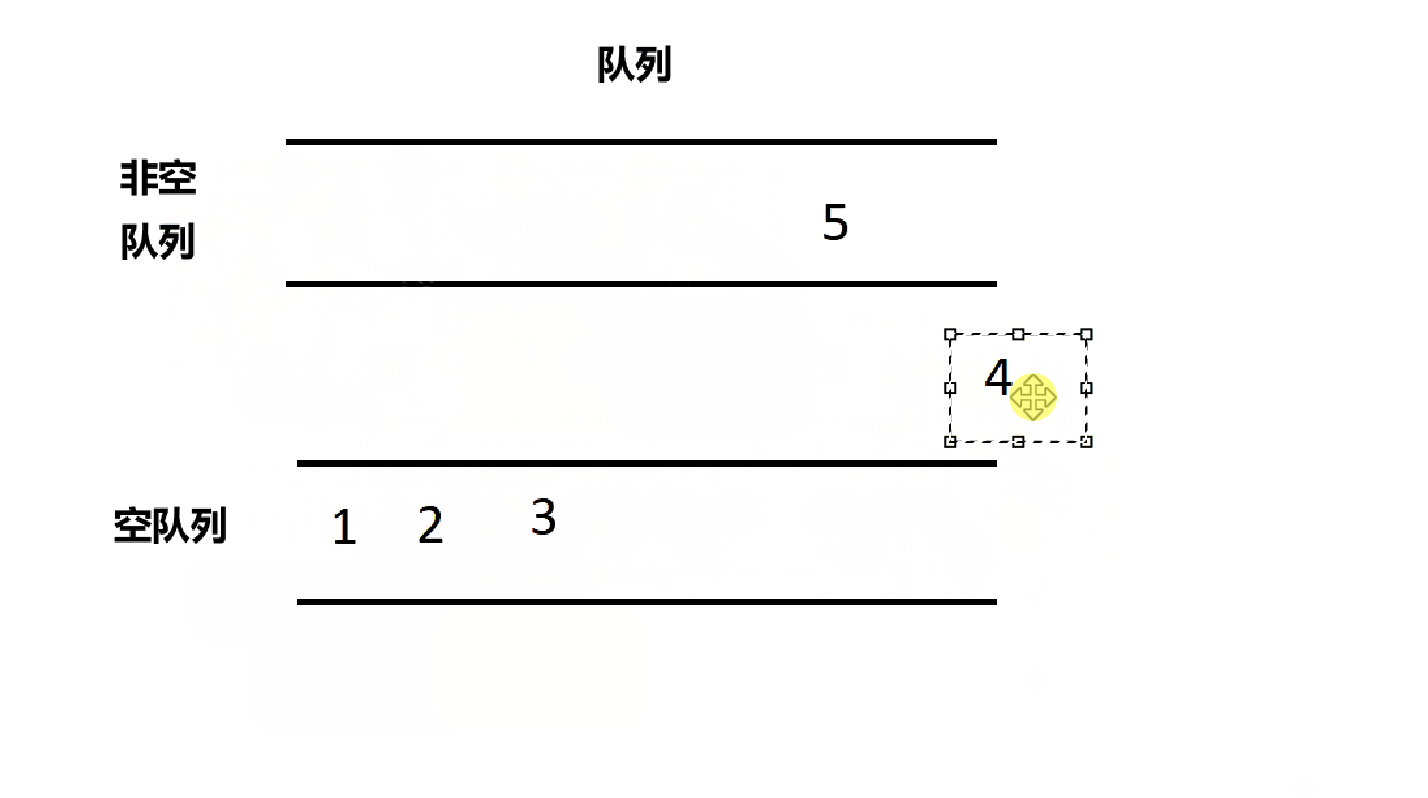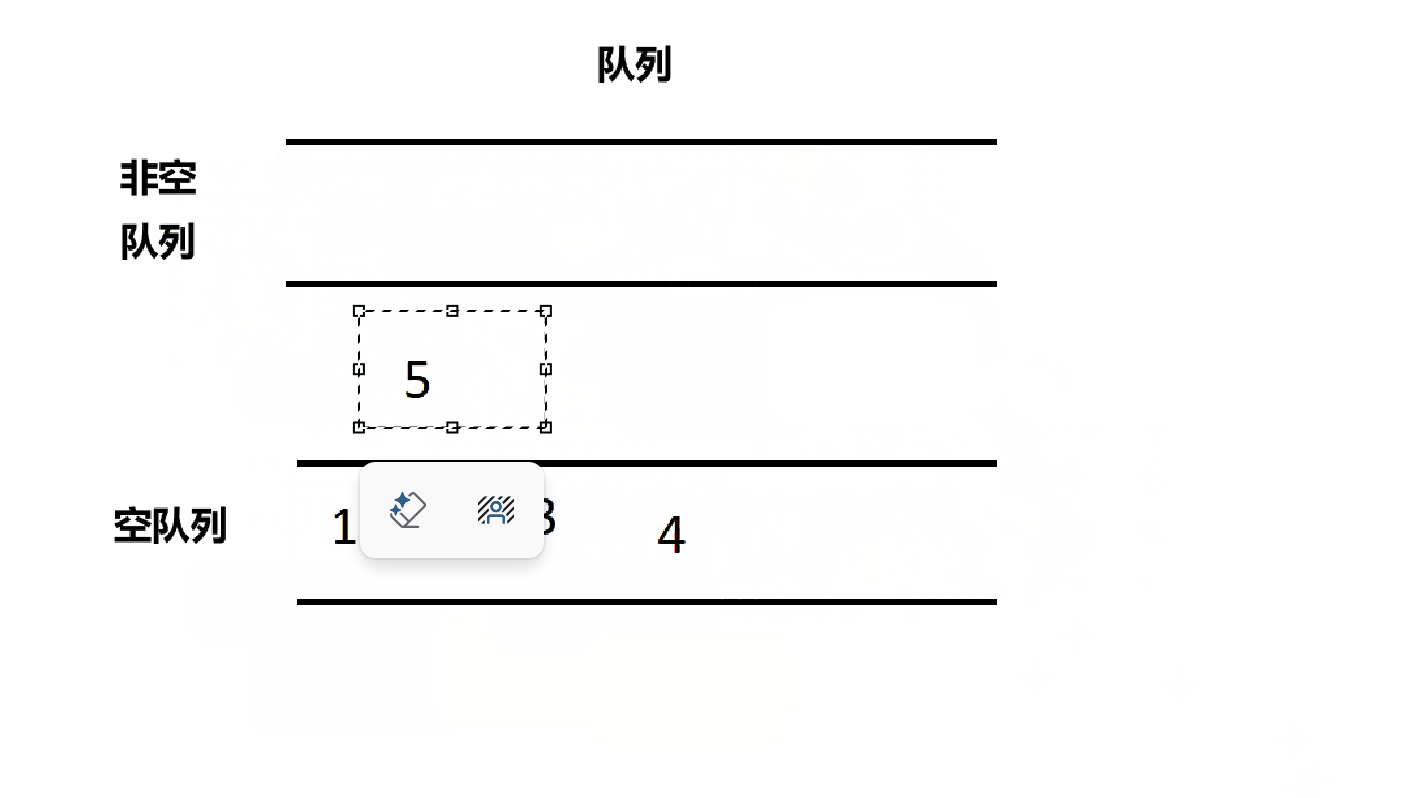
出栈的时候要先找出哪个是空队列,哪个是非空队列,然后将非空队列的n-1个数据依次放到空队列,然后非空队列剩下的那个元素出队就可以了。
cpp
int myStackPop(MyStack* obj)
{
//寻找谁是空队列
Queue* emptyq = &obj->q1; //要修改队列本身,必须用指针
Queue* nonemptyq = &obj->q2;
if(QueueEmpty(emptyq) != true)
{
emptyq = &obj->q2;
nonemptyq = &obj->q1;
}
//不为空的队列向空队列输送n-1个元素
int size = QueueSize(nonemptyq);
for(int i =0 ; i <size-1 ;i++)
{
int temp = QueueTop(nonemptyq);
QueuePush(emptyq , temp);
QueuePop(nonemptyq);
}
//原本不为空的队列取队头,出队
int count = QueueTop(nonemptyq);
QueuePop(nonemptyq);
return count;
}4.1.5、获取栈顶元素
这个简单,直接返回非空队列的末尾元素就可以了
cpp
int myStackTop(MyStack* obj) {
assert(obj);
//直接返回不为空队列的尾元素就好了
if(QueueEmpty(&obj->q1) == true)
{
return QueueEnd(&obj->q2);
}
else
{
return QueueEnd(&obj->q1);
}
}4.1.6、判断栈是否为空
栈要为空,那么两个队列都必须为空,是且的关系
cpp
bool myStackEmpty(MyStack* obj) {
assert(obj);
if(QueueEmpty(&obj->q1) == true && QueueEmpty(&obj->q2) == true)
{
return true;
}
else
{
return false;
}
}4.1.7、栈的销毁
销毁要按照顺序来,先销毁队列,再销毁栈
cpp
void myStackFree(MyStack* obj) {
assert(obj);
QueueDestory(&obj->q1);
QueueDestory(&obj->q2);
free(obj);
obj == NULL;
}4.2、用栈实现队列

根据上一次用队列实现栈的经验,这次用栈实现队列也应该大差不差,一个栈用来存放数据,一个栈用来出数据。不同的是,这两个栈是固定的,因为序列的顺序不能变。
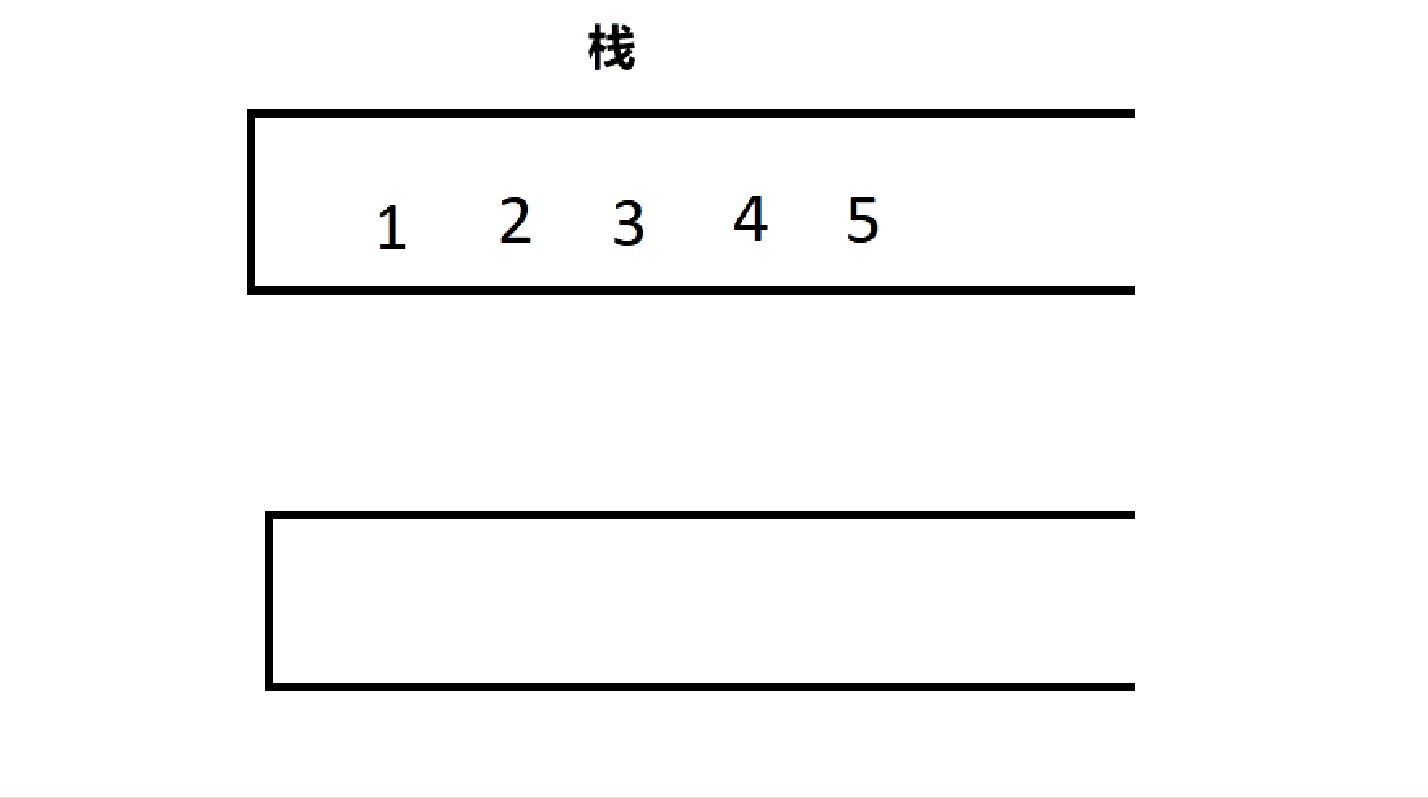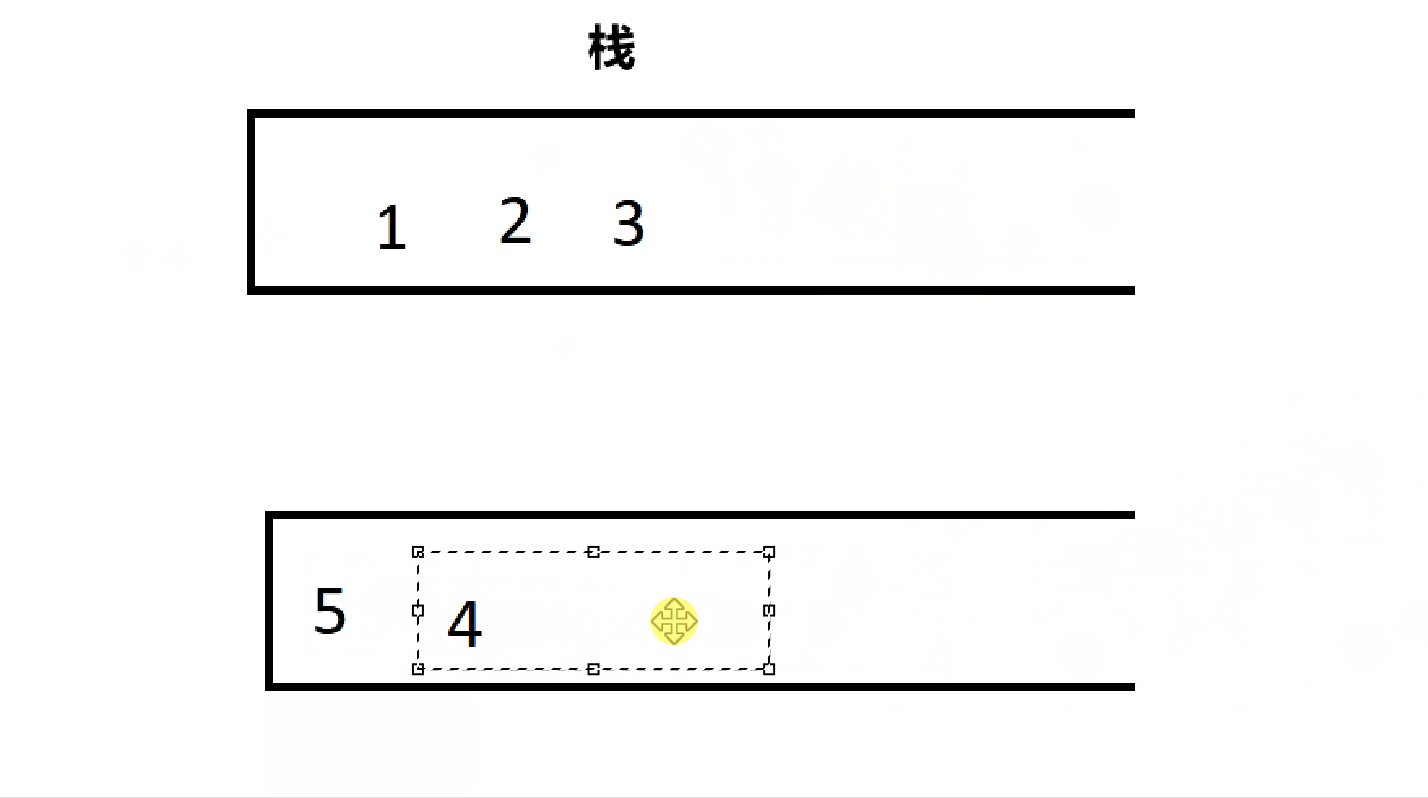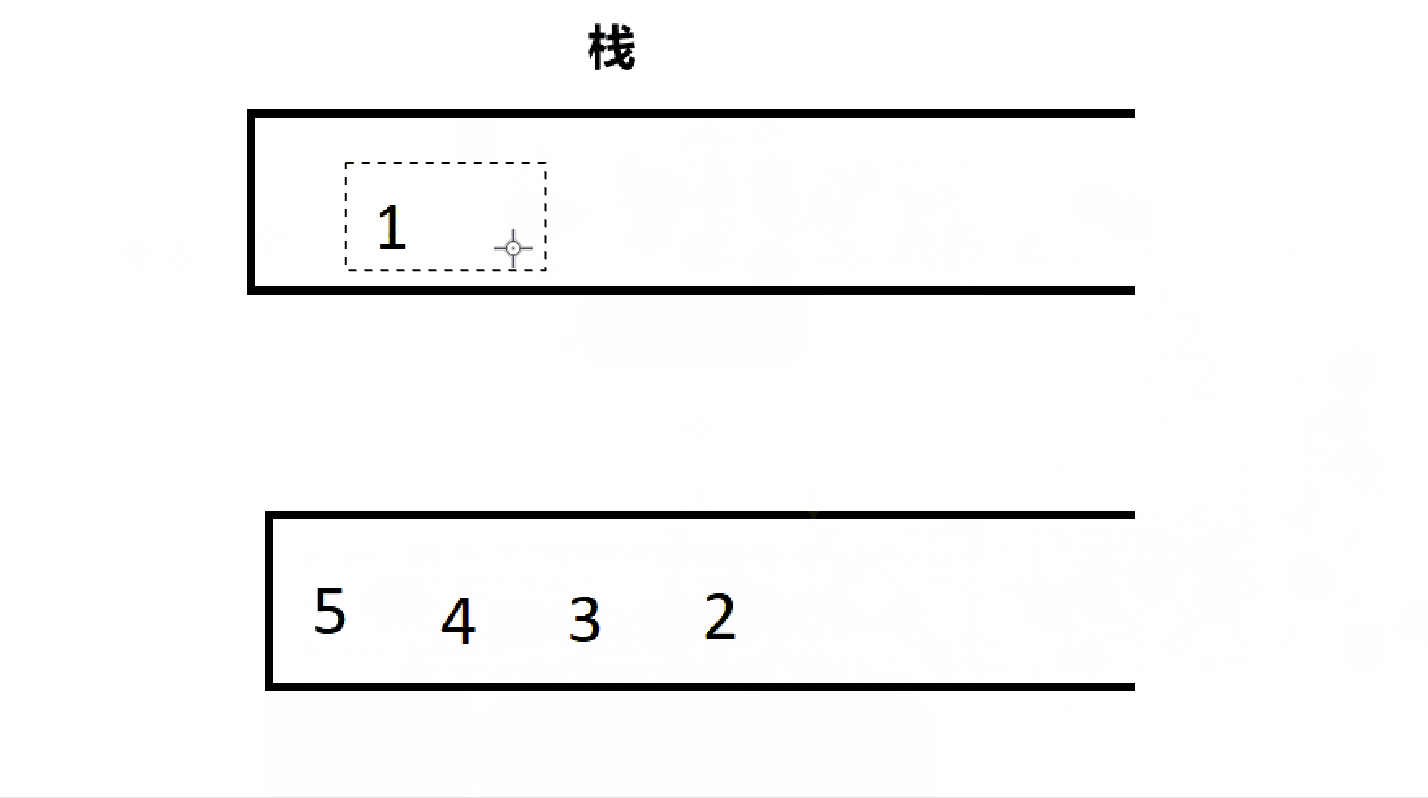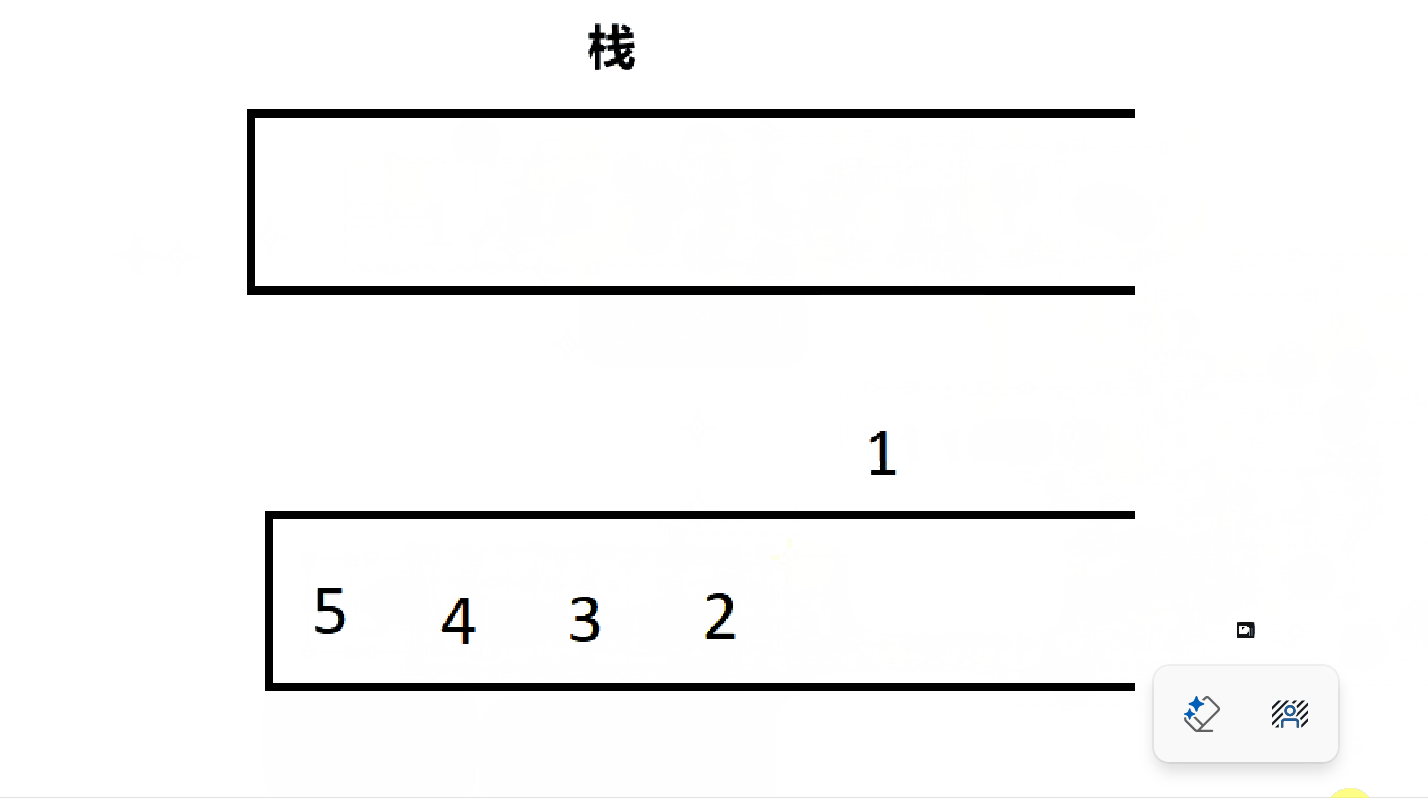
4.2.1、队列的结构
很明显,该队列的成员是两个栈(关于栈的函数上篇文章里有)
cpp
typedef struct MyQueue{
Stack stPush;
Stack stPop;
} MyQueue;4.2.1、出队
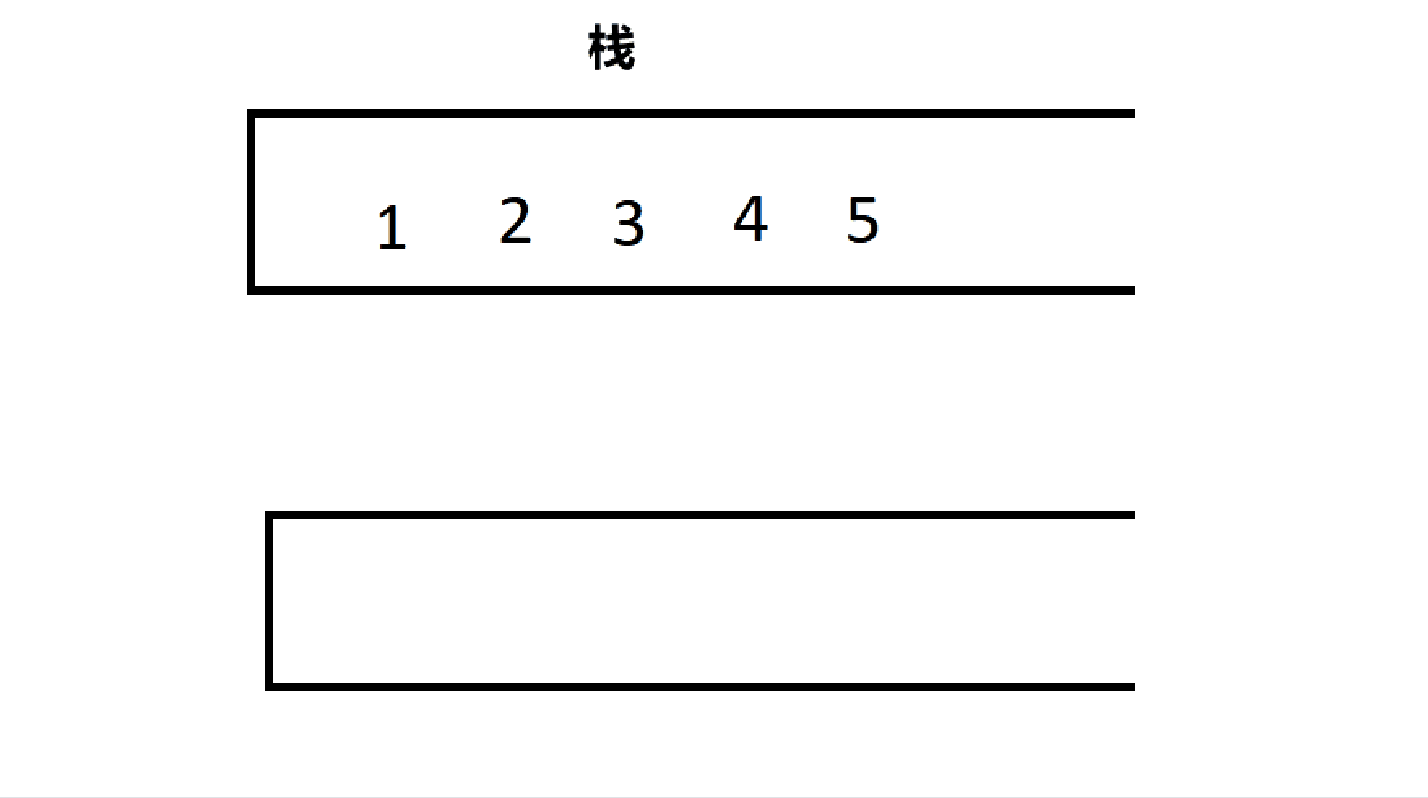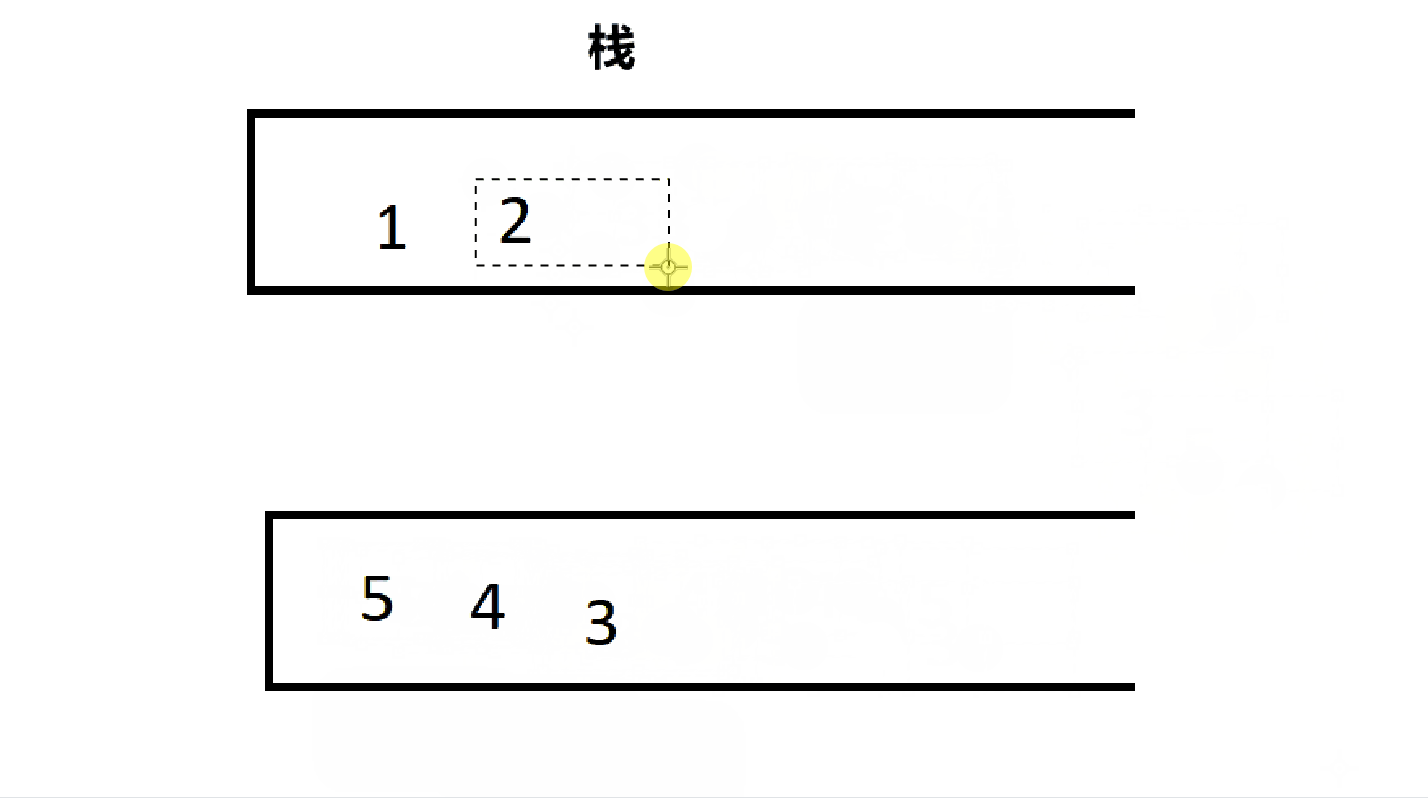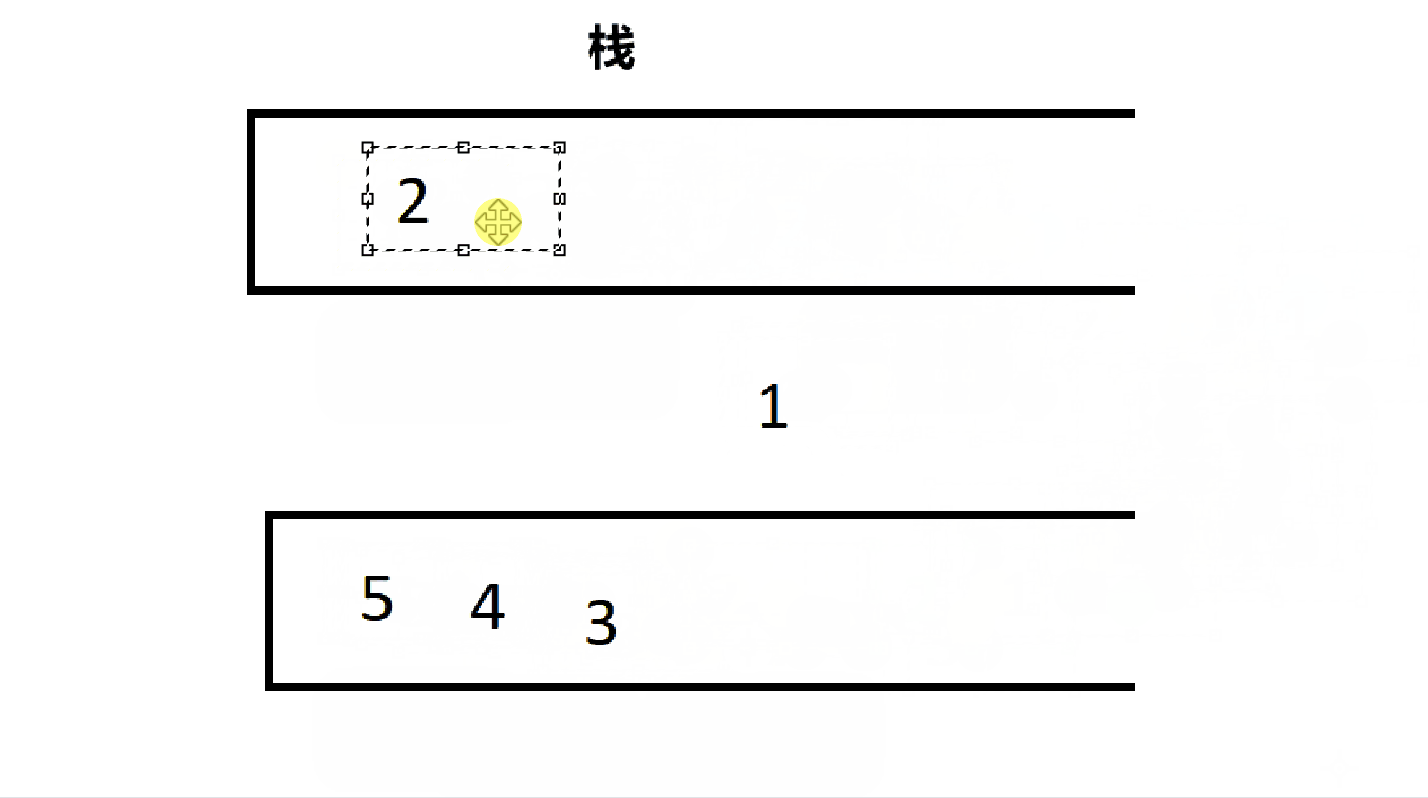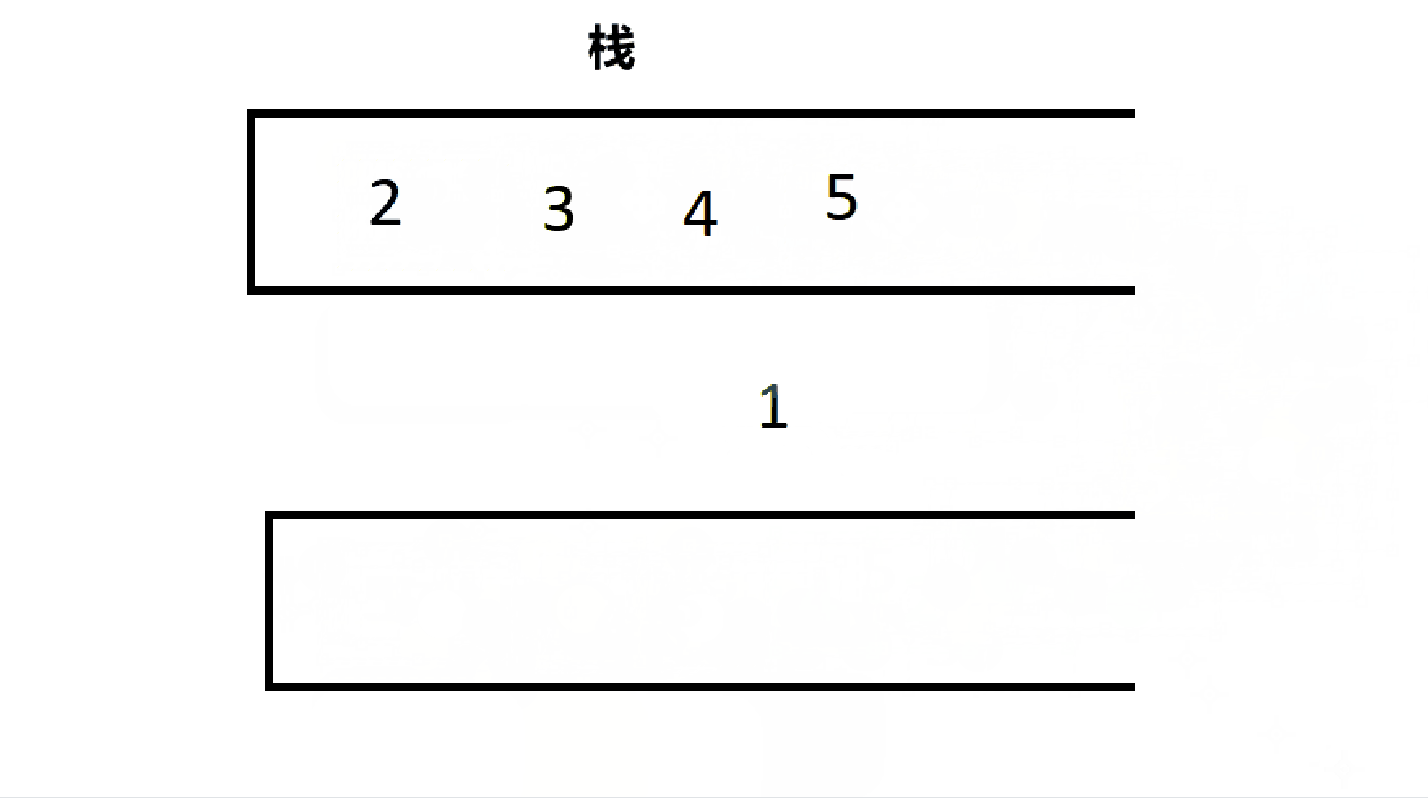
代码如下:
cpp
int myQueuePop(MyQueue* obj) {
assert(obj);
//将存放数据的栈依次出栈,在放入另一个栈中
int size = obj->stPush.top;
for(int i = 0 ; i< size ;i++)
{
int tmd = StackTop(&obj->stPush);
StackPush(&obj->stPop , tmd);
StackPop(&obj->stPush);
}
//另一个栈出栈
int data = StackTop(&obj->stPop);
StackPop(&obj->stPop);
//将另一个栈中剩余的数据依次倒回存放数据的栈
size = obj->stPop.top;
for(int i = 0 ; i <size; i++)
{
int tmd = StackTop(&obj->stPop);
StackPush(&obj->stPush , tmd);
StackPop(&obj->stPop);
}
return data;
}4.3、设计循环队列


看题目要求,在设置构造器的时候,需要设定队列长度为 k ,如果还是选择队列的话,一口气要创造 k 个节点,然后还要一次连接起来,麻烦;还不如直接选择顺序表,一口气创造 k 个元素的空间大小,简单(不用相互连接)。
但是,在不添加新的结构成员的情况下,如何判断循环队列是否为空呢?
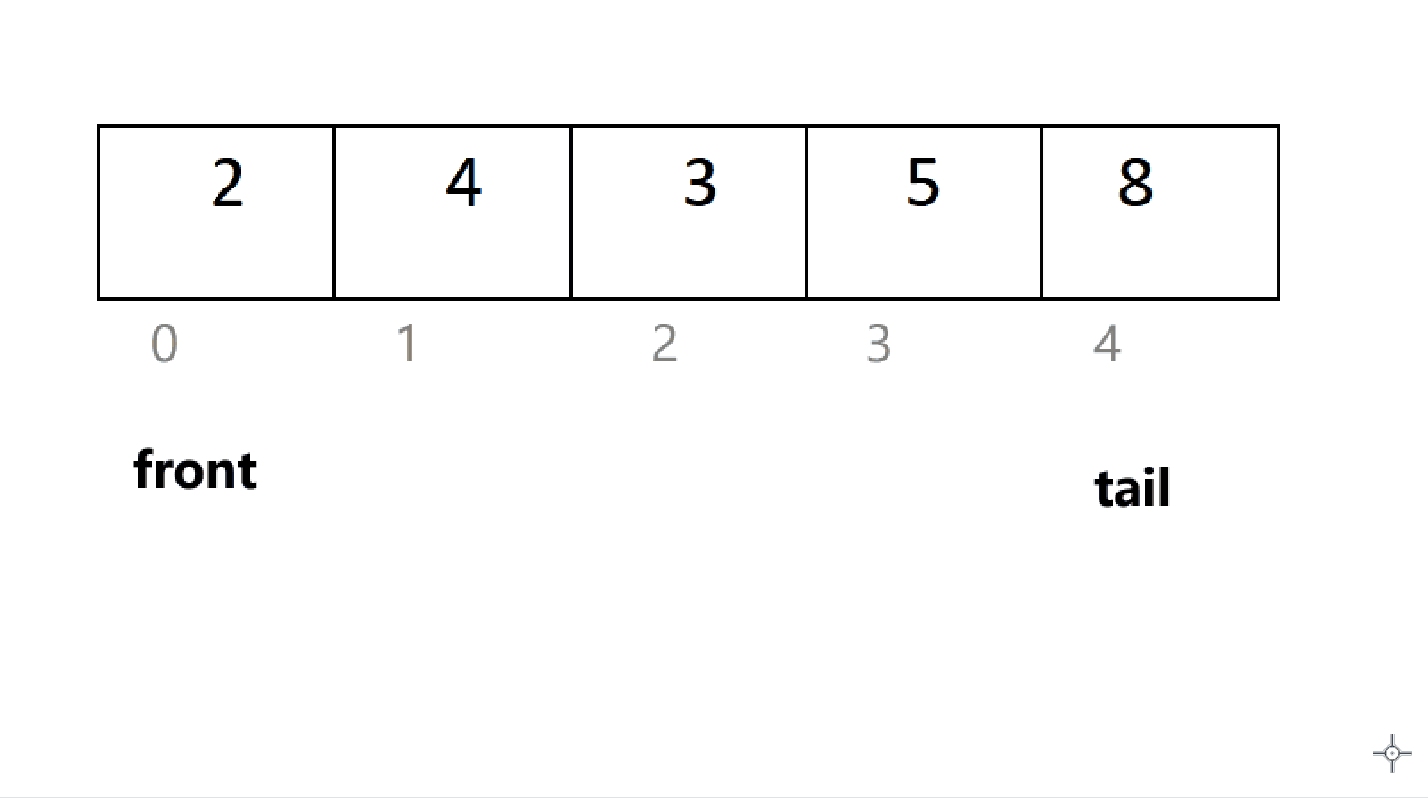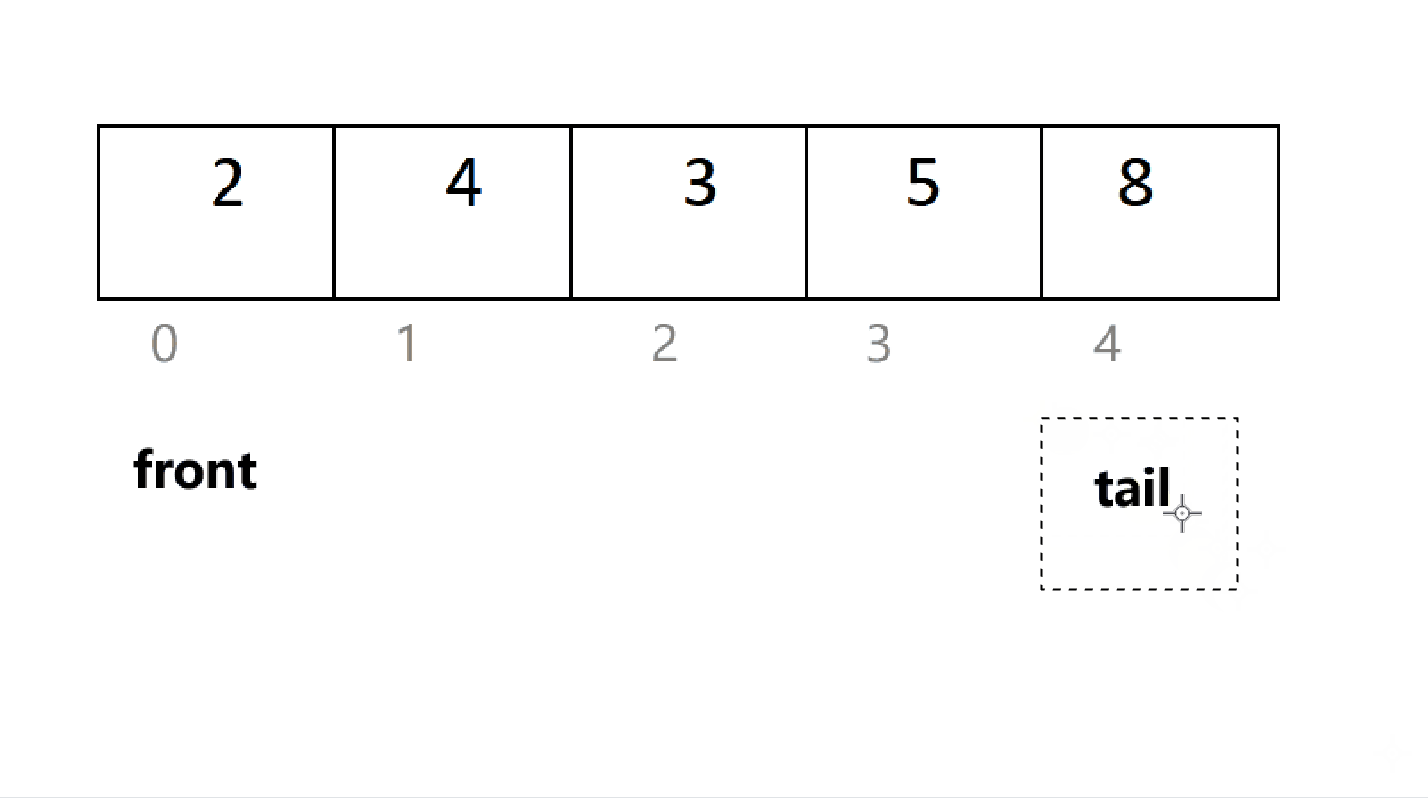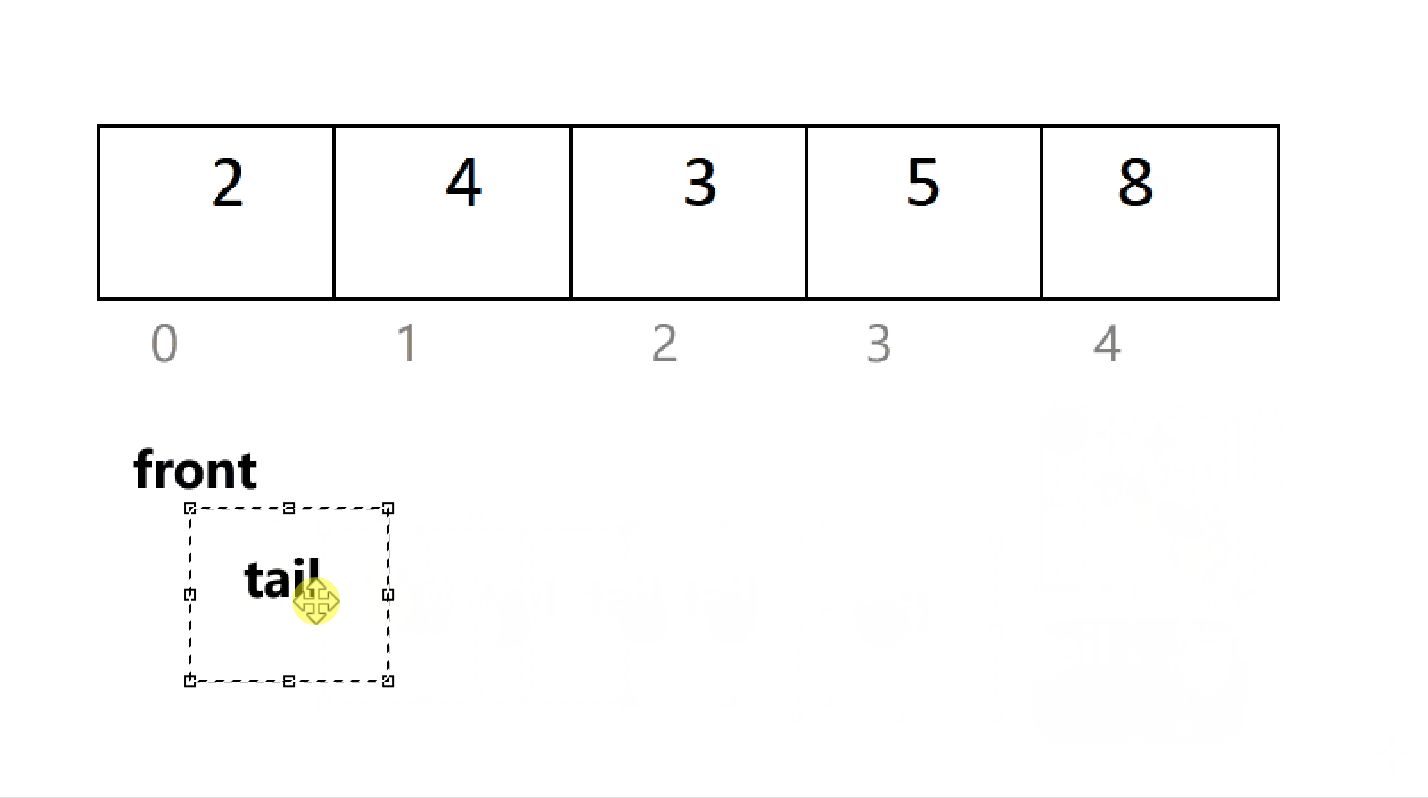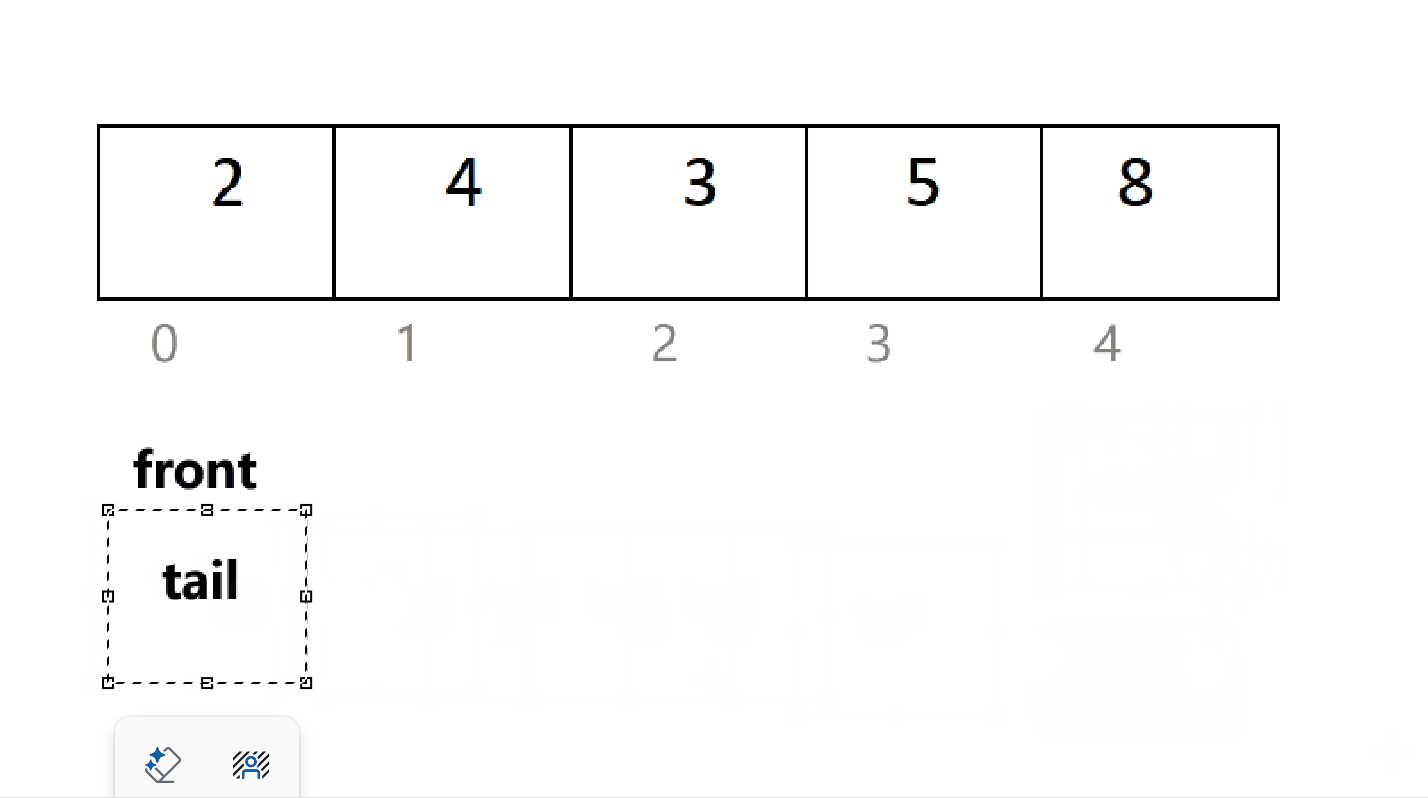
当插入最后一个元素后,由于循环,tail 再次等于 front,此时,对队满;但是,一开始 tail 也等于 front ,为队空。一时间无法区分队满和队空。
解决办法是,开辟 k+1个元素的空间就可以了。
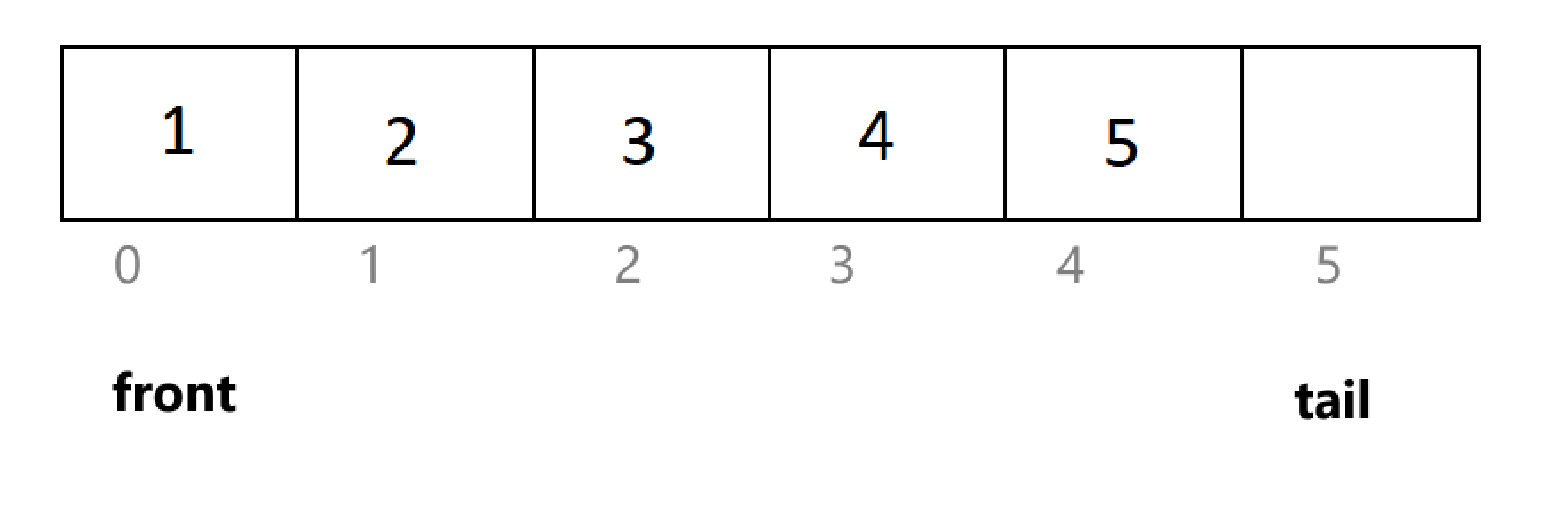
当 tail / (k+1) == front 时,队满,当 (tail+1)%(k+1)== front 时为空。
4.3.1、循环队列的定义
使用顺序表实现,所以该循环队列结构应该包含:顺序表指针,容量,有效元素个数,首元素下标,末尾元素下标。(有效元素个数和末尾元素下标可以合并)
cpp
typedef struct {
int* arr; //顺序表指针
int front; //首元素下标
int tail; //尾元素下标
int capacity; //容量
} MyCircularQueue;4.3.2、循环队列是否为空,是否为满
由前面讲的思路可以简单求的:
cpp
//判断循环队列是否为空
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
assert(obj);
return obj->tail == obj->front;
}
//判断循环队列是否为满
bool myCircularQueueIsFull(MyCircularQueue* obj) {
assert(obj);
return (obj->tail+1)%(obj->capacity+1) == obj->front;
}4.3.3、返回循环队列末尾元素
与顺序表一样,直接通过尾元素下标求得,但是,由下面的情况:
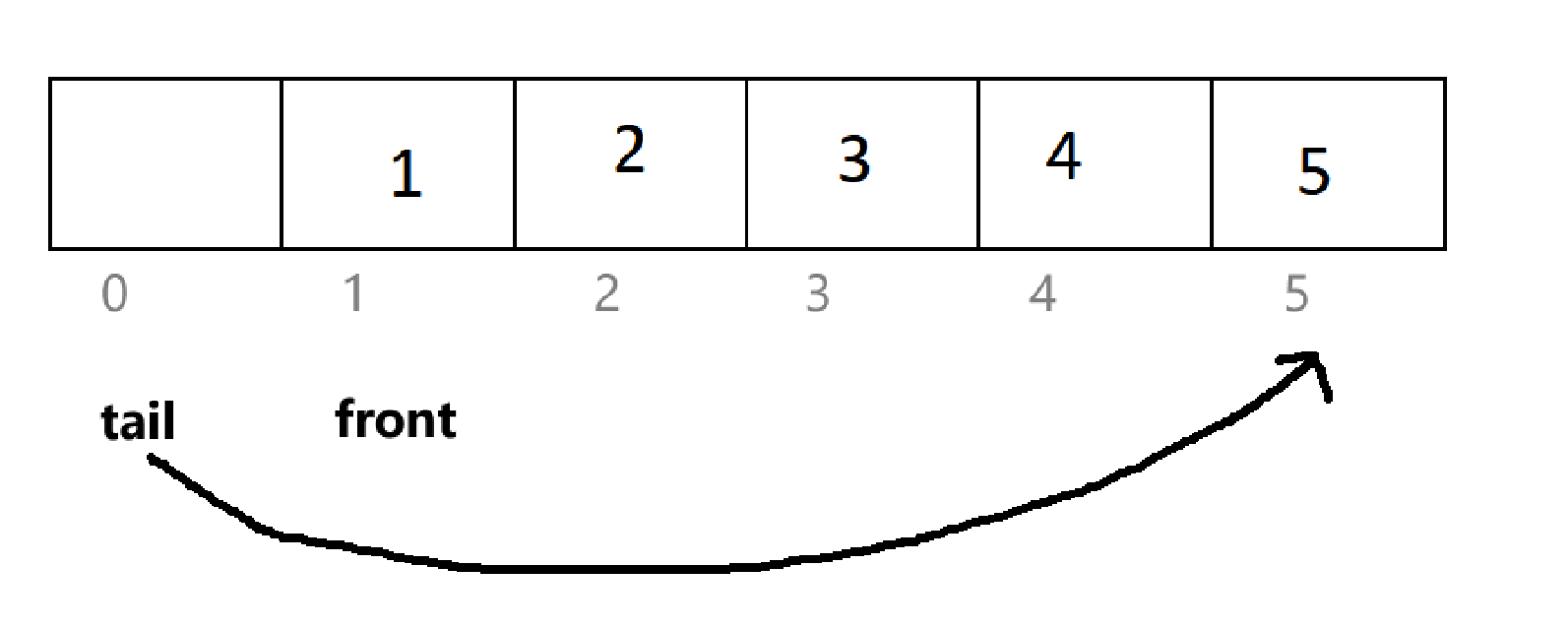
tail -1 就变成负数了,所以需要进行一定的修正。
cpp
int myCircularQueueRear(MyCircularQueue* obj) {
assert(obj);
if(obj->front == obj->tail)
{
return -1;
}
else
{
int end = obj->tail-1;
//进行修正
if(end <0)
{
end = obj->capacity;
}
return obj->arr[end];
}
}五、结语
队列是线性表中的重要组成部分,扎实掌握队列是未来写好代码的基础,要多加练习。下篇博客将会带来树的讲解,如果有什么不足和疑问可以写在讨论区,或者直接私信我哦。