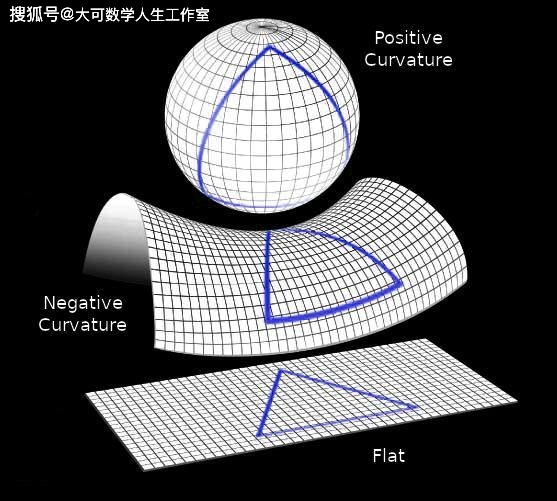
将平面视为半径无限大的球面,是一种深刻的几何与哲学视角,它揭示了平面与曲面在极限条件下的内在统一性。以下从数学定义、几何性质、物理意义三个层面展开分析:
一、数学定义:从球面到平面的极限


二、几何性质:曲率与平行性的统一
-
高斯曲率的消失
球面的高斯曲率 K=R21,当 R→∞ 时,K→0,平面成为曲率为零的曲面 。此时,平面上的"直线"可视为球面大圆的极限(如赤道线)。
-
平行线的重新定义
在球面上,任意两条大圆必相交(如经线交于两极),因此不存在严格平行线。但当 R→∞,球面趋近于平面,大圆间的夹角趋近于零,此时可定义"极限平行"为平面中的平行线。
三、物理意义:宇宙学中的视角
-
宇宙模型的启示
若宇宙是有限无界的闭合空间(如三维球面),其曲率半径 R 可能远大于可观测宇宙尺度。此时,局部观测者会感知到近似平直的时空(如广义相对论中平坦的闵可夫斯基时空是弯曲时空的局部近似)。
-
引力与几何的关联
爱因斯坦场方程表明,物质分布决定时空曲率。在真空且无物质区域(R→∞),时空趋近于平直,即平面是弯曲时空的极限情形。
四、哲学思考:有限与无限的辩证
-
几何的相对性
平面与球面的区分依赖于观测尺度。在微观尺度(如原子级),平面可能显现晶格结构;在宏观尺度(如地球表面),曲面可近似为平面。这种相对性体现了**"局部平直,整体弯曲"的几何哲学。**
-
数学抽象的力量
通过极限思想,数学家将**看似对立的几何对象(平面与曲面)统一于同一框架。**这种抽象化思维是现代数学与物理学发展的核心方法。
总结
将平面视为半径无限大的球面,不仅是数学上的严格定义,更是理解几何本质、宇宙结构乃至人类认知局限的重要视角。它揭示了:
- 局部与全局的关系:平面是曲面的局部近似;
- 有限与无限的统一:通过极限过程,有限曲率可趋近于零;
- 抽象与现实的桥梁:数学理想模型(如无限大球面)可精确描述物理现实(如近似平直的时空)。