图算法趣味学——桥和割点

在本章中，我们将讨论连通性的另一个方面：在无向图中，对于保持连通分量完整性至关重要的节点和边。这些节点和边分别被称为割点 和桥。了解哪些节点或边对于保持连通性是必不可少的，在许多现实问题中都非常重要。每当我们需要确保网络中不存在单点故障时，就需要找到其桥和割点。

在正式定义桥和割点之后，本章将提供一些现实场景的示例，说明这些概念的应用，例如为一组岛屿设计稳健的交通网络，或为一个邪恶巫师建造最精妙的秘密迷宫。随后，我们将介绍两种算法，以高效地在无向图中搜索这些关键元素，这些算法基于第4章介绍的深度优先搜索（DFS）算法。

桥和割点的定义

为了使无向图中每一对节点都能互相到达，它们必须属于同一个连通分量。在第3章中，我们学习到，无向图的一个连通分量是节点的子集 <math xmlns="http://www.w3.org/1998/Math/MathML"> V ′ ⊆ V V' \subseteq V </math>V′⊆V，使得对于任意的 <math xmlns="http://www.w3.org/1998/Math/MathML"> u ∈ V ′ 和 v ∈ V ′ u \in V' 和 v \in V' </math>u∈V′和v∈V′，节点 <math xmlns="http://www.w3.org/1998/Math/MathML"> u u </math>u 都可以到达节点 <math xmlns="http://www.w3.org/1998/Math/MathML"> v v </math>v。

举一个具体例子：考虑一组通过渡轮相连的岛屿。节点代表岛屿，边代表岛屿之间的渡轮航线。为了提供完整的出行选择，交通规划者希望形成的图是一个单一的连通分量。也就是说，人们必须能够在渡轮网络上在任意两个岛屿之间旅行，无论是通过直接航线，还是经过一系列中转。

图 11-1 展示了一个示例图，其中包含两个独立的连通分量： <math xmlns="http://www.w3.org/1998/Math/MathML"> { 0 , 1 , 2 , 4 , 5 } 和 { 3 , 6 , 7 } \{0, 1, 2, 4, 5\} 和 \{3, 6, 7\} </math>{0,1,2,4,5}和{3,6,7}。

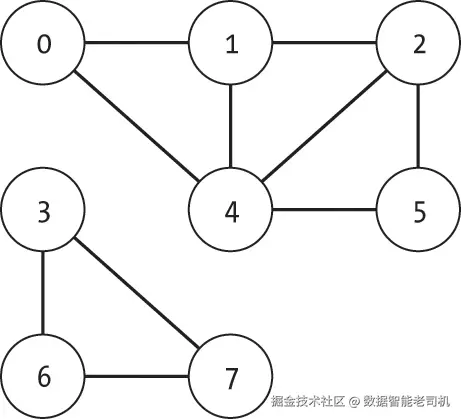
桥是指一条边，其移除会将原本的单一连通分量拆分成两个不相交的连通分量。图 11-2(a) 展示了一个示例图，其中包含两条桥：(1, 2) 和 (4, 5)。移除任意一条边都会将原本的单一连通分量拆分为两个。若同时移除这两条边，则图会被拆分成三个独立的连通分量，如图 11-2(b) 所示。

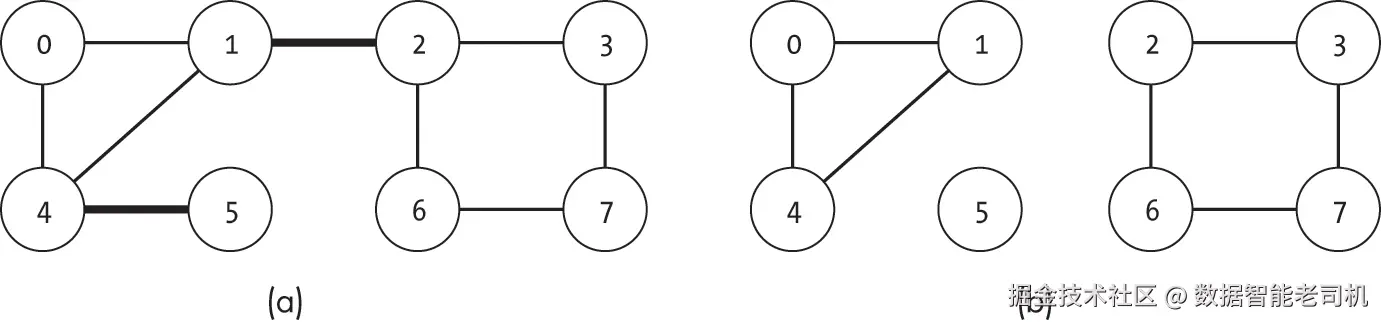
同样，割点（或称切割顶点）是指一个节点，其移除会将一个连通分量拆分成两个或多个不相交的连通分量。例如，图 11-3 中的图有三个割点：阴影标记的节点 1、2 和 4。

图 11-4 展示了在图 11-3 中，分别移除每个割点所造成的影响。

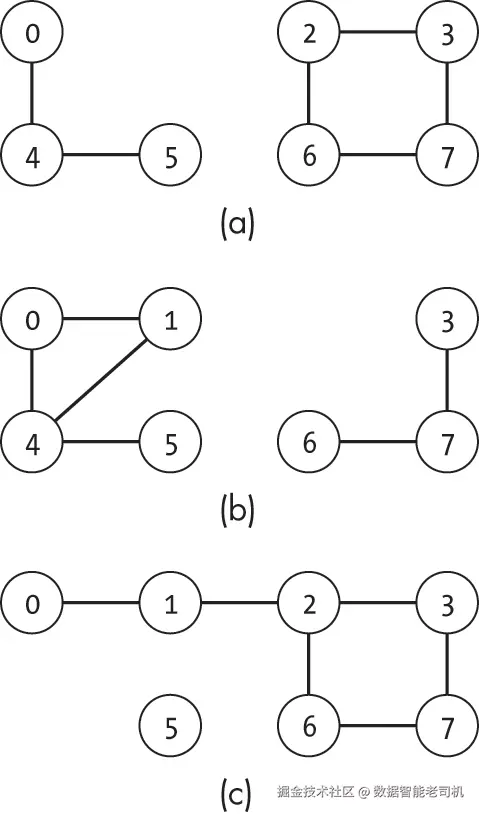
在图 11-4(a) 中，移除节点 1 会产生两个连通分量：{0, 4, 5} 和 {2, 3, 6, 7}。图 11-4(b) 显示，移除节点 2 会产生分量 {0, 1, 4, 5} 和 {3, 6, 7}，而移除节点 4 则会产生分量 {0, 1, 2, 3, 6, 7} 和 {5}，如图 11-4(c) 所示。

应用场景

识别图中的桥和割点对于了解网络中的单点故障至关重要。本节提供了一些现实世界中寻找桥和割点的应用示例。我们首先展示如何应用这些概念来构建具有弹性的渡轮网络，然后探讨如何将相同技术扩展到防止疾病传播或构建最佳魔法迷宫的场景。

设计弹性网络

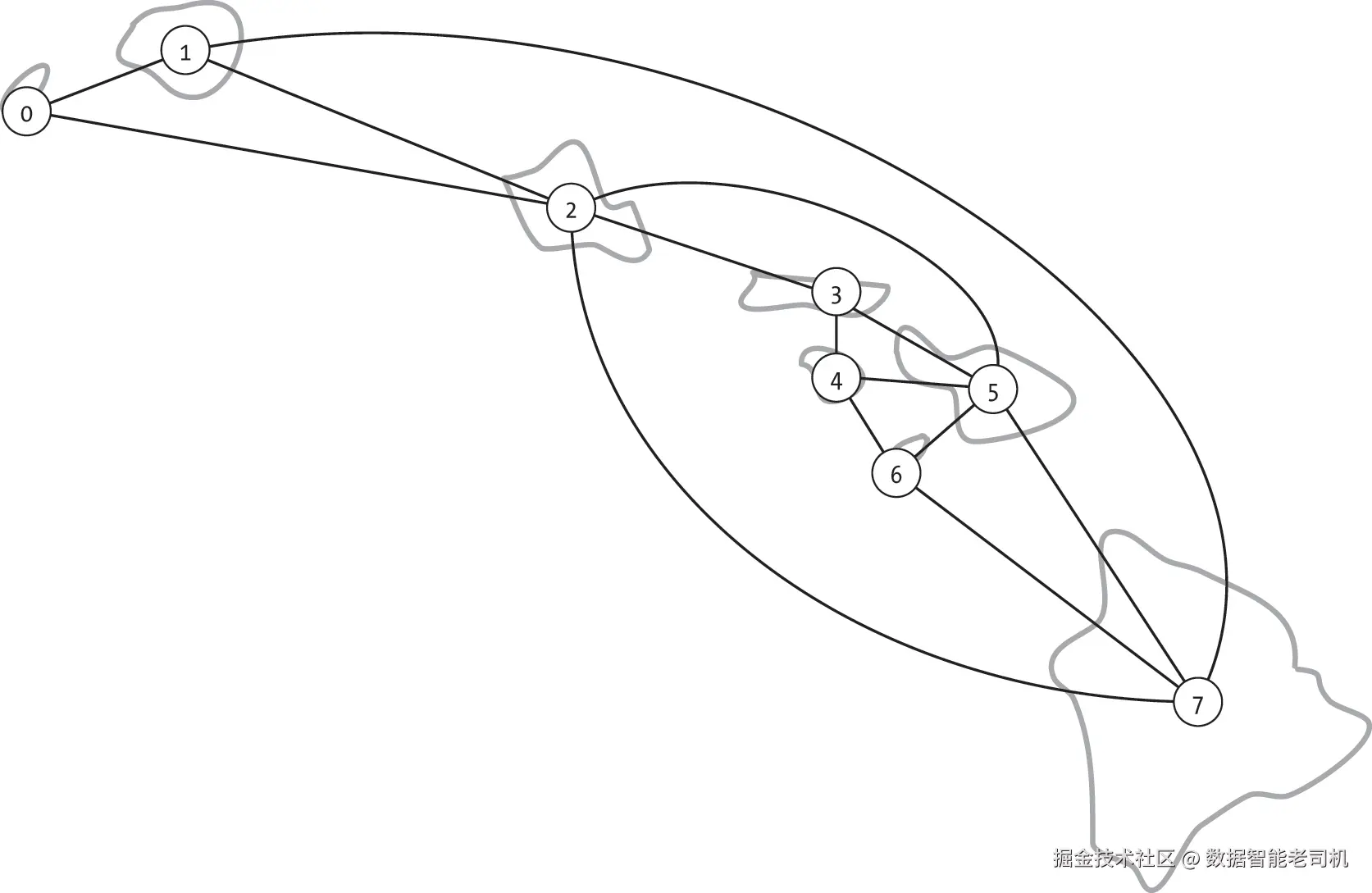
一个弹性网络需要能够优雅地处理单个边或节点的丢失，而不会丧失连通性。延续上一节的岛屿示例，我们考虑夏威夷八个岛屿之间的两个假设渡轮网络，如图 11-5 和图 11-6 所示。

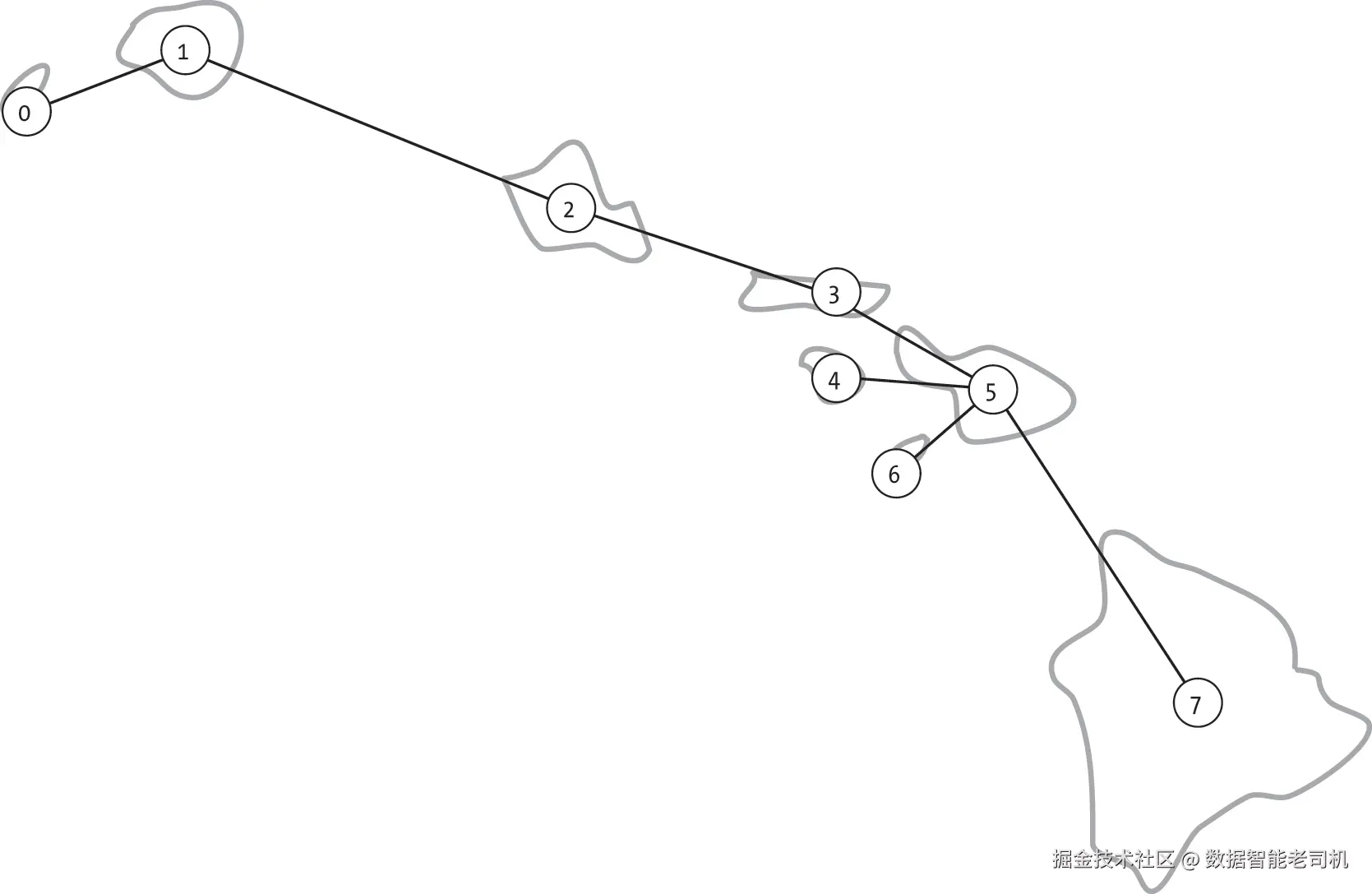
图 11-5 展示了连接这八个岛屿所需的最小渡轮网络。如果所有渡轮运行正常，任何两座岛屿之间都可以通行。虽然有人可能需要经过多次中转才能到达目的地，但总会存在一条路径。

然而，该网络非常脆弱。如果从瓦胡岛（O'ahu，节点 2）到莫洛凯岛（Moloka'i，节点 3）的渡轮停运，网络就会被分成两部分。人们无法再从毛伊岛（Maui，节点 5）前往尼豪岛（Ni'ihau，节点 0）。图中的每条渡轮路线都是一座桥。任何一条路线的中断都会导致至少一个岛屿失去连通性。同样，图 11-5 中的许多节点是割点。如果瓦胡岛（节点 2）的渡轮码头因天气关闭，就会导致考爱岛（Kaua'i，节点 1）与毛伊岛（节点 5）失去连通。

通过了解网络中的桥和割点，规划者可以设计一个更稳健的网络，不存在桥，如图 11-6 所示。即便某条渡轮线路中断（移除一条边），任何两座岛屿之间的通行也不会被切断。例如，如果瓦胡岛（节点 2）到莫洛凯岛（节点 3）的渡轮停运，旅客仍然可以通过其他路线从毛伊岛（节点 5）到达尼豪岛（节点 0）。该网络同样没有割点。例如，如果毛伊岛的渡轮码头关闭，只会影响该岛本身的连通性。

我们可以将这些概念扩展到交通系统以外的领域，如计算机网络、电网、通信网络或污水处理系统。虽然通常希望构建没有桥或割点的图，但这并非总是可行。然而，了解网络的薄弱环节仍然有助于规划和决策。

防止疾病传播

考虑感冒如何在社交网络中传播。为简单起见，假设你必须与生病的人接触才能被感染；你不会从从未见过的人那里感染感冒。如果图中的边表示人与人之间的实际互动，那么病毒只能在相邻节点之间传播。

我们可以利用桥和割点的概念来建模或阻止疾病传播。例如，与前同事的那次咖啡聚会就像一座桥，使感冒能在原本不相连的两组人之间传播：你的前同事和现在的同事。一个选择自我隔离、阻断病毒在群体间传播的人就是一个割点。通过几周不参加任何活动，你可以帮助防止感冒在不同社交圈之间传播。你的跑步朋友、数据结构读书小组成员以及同事们都只能局限于各自的感冒，而不会通过你相互传染。

设计魔法迷宫

与前两种情况不同，这里我们想最大化桥和割点的作用。想象一个邪恶巫师决定在迷宫中布置最有效的陷阱。一条隧道如果是连接迷宫两部分的唯一通道，就是一座桥。如果一部分包含入口，另一部分包含目标，巫师就知道，任何认真的冒险者都必须经过这条隧道，这使它成为放置最佳陷阱的理想位置。同样，一间房间如果必须经过才能从迷宫一部分移动到另一部分，就是一个割点------放置高级怪物的理想地点。

在更常见的场景中，我们可以使用相同的技巧，在关键高速公路（桥）上设置收费站，或在机场航站楼交汇处（割点）设置信息亭。在这些情况下，我们利用了这样一个事实：从图的一部分前往另一部分的人必须经过这个单一节点或边。了解图的连通性，使我们能够优化可能稀缺或昂贵的资源。

桥查找算法

计算机科学家 Robert Tarjan 提出了一系列有用的算法，通过深度优先搜索树的属性来理解图结构。本节介绍一种在无向图中查找桥的算法。该算法从任意节点开始深度优先搜索，同时记录使用的边和节点首次被访问的顺序（顺序索引或前序索引，记作 order(u)）。我们可以利用这些信息查找桥：检查深度优先搜索树中的一条边是否提供了到达其子树节点的唯一路径。深度优先搜索树 T 中未出现的边可以直接排除为桥，因为我们在不使用它们的情况下已经可以到达节点。换句话说，只需考虑树 T 中的边。

图 11-7 展示了一个示例图及其对应的深度优先搜索树（以节点 0 为根）的两种表示。图 11-7(a) 显示初始图。图 11-7(b) 显示从节点 0 开始的深度优先搜索树；每个节点外的数字表示顺序索引。图 11-7(c) 显示相同的树，其中未遍历的边以虚线表示。这些未遍历的边称为回边（back edges），它们指向在深度优先搜索过程中已经访问过的节点。

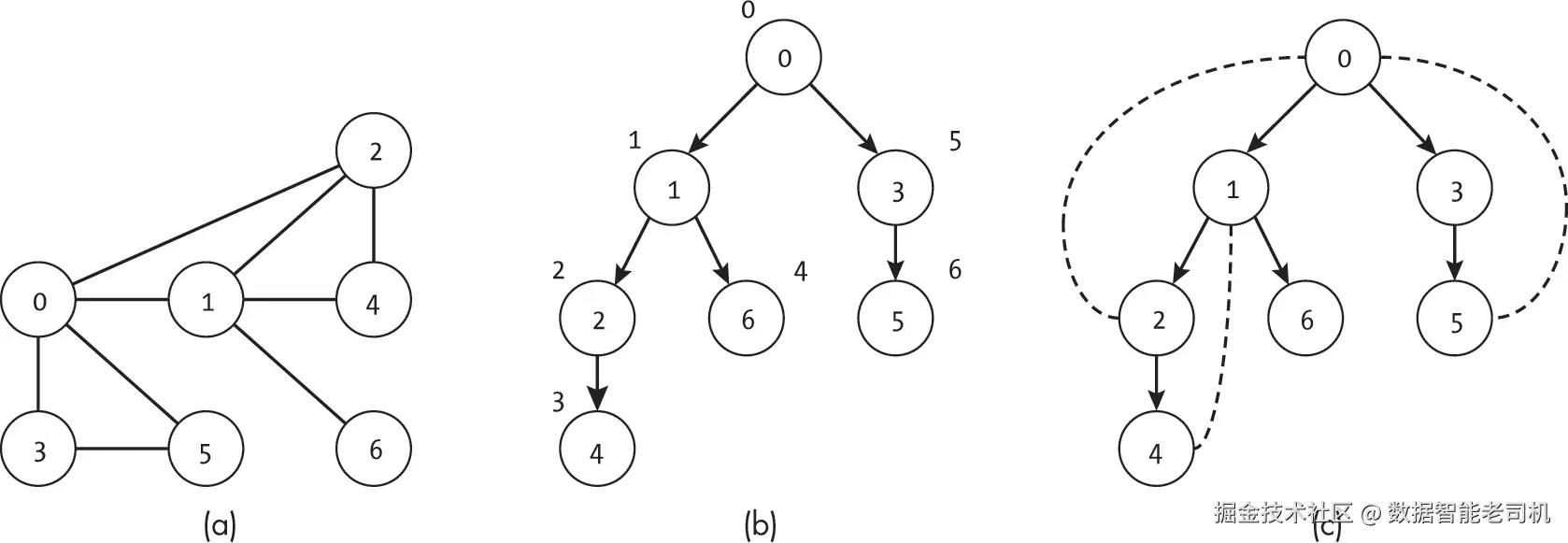
我们可以通过观察通向深度优先搜索树 T 子树的边来识别桥。具体来说，如果某个子树中的节点只与同一子树内的节点相邻，那么通向该子树的边就是桥。换句话说，如果边 (v, u) 是一条桥，则除了通过进入 (v, u) 的这条边外，没有其他方式可以进入或离开节点 u 的子树。图 11-7(a) 中的边 (1, 6) 就是这样一个例子，它提供了进入或离开以节点 6 为根的子树的唯一路径。相比之下，边 (0, 3) 并不是桥，因为节点 5 有一条边返回到节点 0。

该算法的关键在于，我们可以观察节点 u 及其子孙邻居的最小和最大顺序索引。根据深度优先搜索的性质，u 的子树中所有节点的顺序索引必须在 [order(u), order(u) + K − 1] 范围内，其中 K 是子树中节点的数量（包括 u 本身）。这是因为搜索在访问 u 后，会依次访问这些节点，而在访问其他子树的节点之前完成。如果 u 的子树中的节点存在顺序索引不在该范围内的邻居，那么指向该邻居的边会提供进入 u 子树的另一条路径。

我们可以通过一个常见的简化方法来处理：任何从子树可达的未访问节点都将在深度优先搜索中被探索，因此它们会包含在子树中。因此，我们只需检查指向顺序索引更低邻居的回边。判断边 (v, u)（其中 v 是 u 的父节点）是否为桥，可以通过检查 u 的子树中是否存在一个邻居 w，使得 order(w) < order(u)，并排除边 (v, u) 本身。如果存在这样的邻居，说明存在一条绕过 (v, u) 的回边，因此 (v, u) 不是桥。反之，如果在排除 (v, u) 的情况下，子树中所有邻居 w 的顺序索引都满足 order(w) ≥ order(u)，那么 (v, u) 就是一条桥。

图 11-7 中的节点 2 就是一个例子。搜索通过边 (1, 2) 到达节点 2，并将其顺序索引设为 2，如图 11-7(b) 所示。要使边 (1, 2) 成为桥，必须不存在其他从该子树出去的路径。然而，节点 2 本身有一条边指向节点 0（顺序索引为 0），提供了另一条替代路径。

相反的情况如图 11-8 所示，以边 (0, 1) 为例。图 11-8(a) 相比图 11-7(a) 略有修改，去掉了边 (0, 2)，因此边 (0, 1) 现在成为一条桥。图 11-8(b) 显示了以节点 0 为根的对应深度优先搜索子树，未遍历的边用灰色表示。两个图中的虚线椭圆表示节点 1 的子树。如图 11-8(b) 所示，节点 1 的子树到顺序索引小于 1 的节点的唯一连接就是边 (0, 1) 本身。

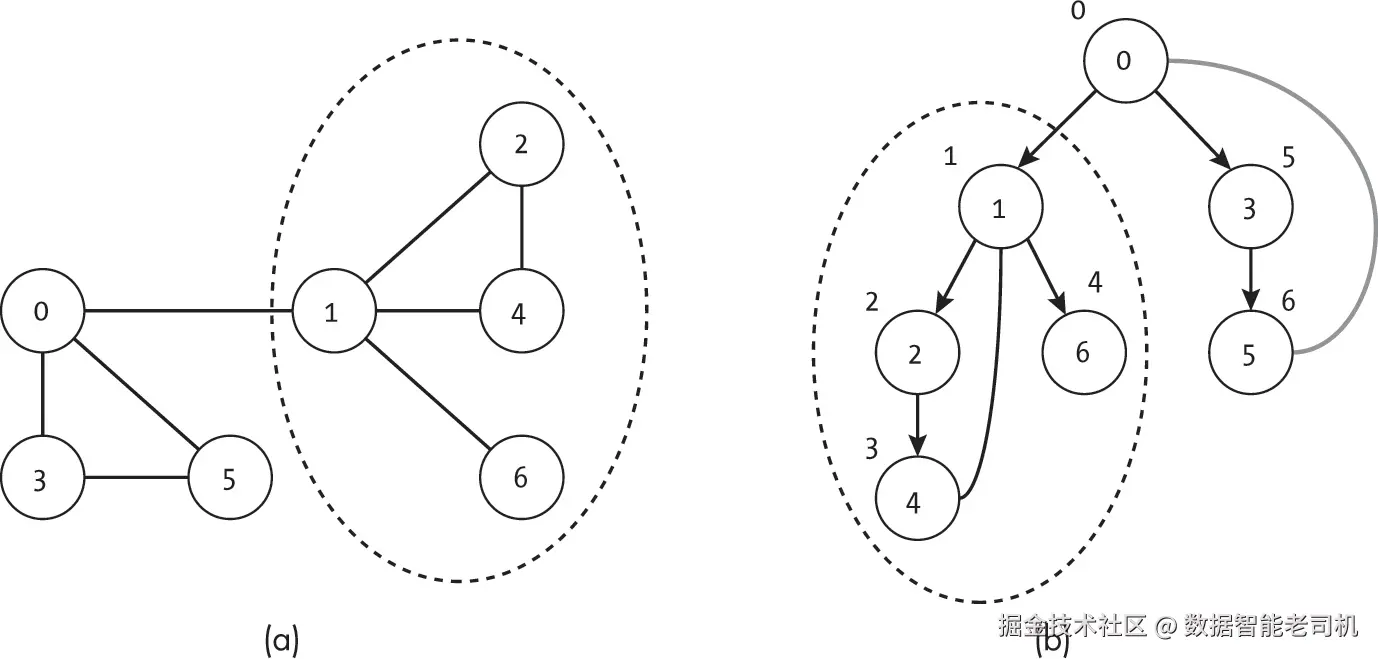
桥检测算法通过记录每个子树中节点邻居的最小顺序索引来检查深度优先搜索树的每个子树。唯一排除的相邻边是子树根节点 u 与其父节点之间的边，因为这是我们正在测试的边。

代码实现

我们可以用一次深度优先搜索来实现桥检测算法。为了简化代码，引入辅助数据结构 DFSTreeStats 来跟踪深度优先搜索访问各节点的顺序信息，包括：

• parent (list)：将每个节点的索引映射到其在深度优先搜索树中的父节点
• next_order_index (int)：存储下一个待分配的顺序索引
• order (list)：将每个节点的索引映射到其顺序索引
• lowest (list)：将每个节点映射到其深度优先搜索子树或邻居中最小的顺序索引（不包括父节点）

DFSTreeStats 封装了这些信息，避免在搜索函数中传递过多参数，同时便于基本赋值和更新。定义如下：

class DFSTreeStats:
    def __init__(self, num_nodes: int): 
      self.parent: list = [-1] * num_nodes  # ❶
      self.next_order_index: int = 0
      self.order: list = [-1] * num_nodes
      self.lowest: list = [-1] * num_nodes

    def set_order_index(self, node_index: int):
        self.order[node_index] = self.next_order_index
        self.next_order_index += 1
        self.lowest[node_index] = self.order[node_index]  # ❷

构造函数将所有信息初始化为初始值 ❶，列表 parent、order 和 lowest 的所有元素设为 -1 表示尚未设置，next_order_index 初始化为 0，为第一个节点做准备。辅助方法 set_order_index() 记录当前节点的顺序索引，并递增下一索引，同时将该节点的最低顺序索引初始化为自身顺序索引 ❷。

接着使用改进的深度优先搜索填充 DFSTreeStats 的条目并寻找桥：

def bridge_finding_dfs(g: Graph, index: int, stats: DFSTreeStats, results: list):
    stats.set_order_index(index)  # ❶

    for edge in g.nodes[index].get_sorted_edge_list():
        neighbor: int = edge.to_node
        if stats.order[neighbor] == -1:  # ❷
            stats.parent[neighbor] = index
            bridge_finding_dfs(g, neighbor, stats, results)
            stats.lowest[index] = min(stats.lowest[index], stats.lowest[neighbor])  # ❸
            if stats.lowest[neighbor] >= stats.order[neighbor]:  # ❹
                results.append(edge)
        elif neighbor != stats.parent[index]:
            stats.lowest[index] = min(stats.lowest[index], stats.order[neighbor])  # ❺

def find_bridges(g: Graph) -> list:
    results: list = []
    stats: DFSTreeStats = DFSTreeStats(g.num_nodes)
    for index in range(g.num_nodes):
        if stats.order[index] == -1:
            bridge_finding_dfs(g, index, stats, results)
    return results

递归辅助函数 bridge_finding_dfs() 首先使用 set_order_index() 设置当前节点的顺序索引及子树可达的最低顺序索引 ❶。然后通过 for 循环检查每个邻居，为保持与其他示例一致，我们使用 get_sorted_edge_list() 按节点索引顺序遍历邻居，虽然排序遍历不是算法正确性的必要条件。

• 如果邻居未被访问（order 未设置） ❷，设置其父节点并递归探索。递归返回后，通过比较子节点的 lowest 与自身的 lowest 更新最小顺序索引 ❸。
• 搜索完成子树探索后，可通过比较子树中任意节点及其邻居的最低顺序索引与子树根节点的顺序索引来判断该边是否为桥 ❹，若是，则加入 results。
• 如果邻居已访问（order 已设置），首先检查邻居是否为父节点，如果是，则忽略；否则检查邻居是否为子树外的节点 ❺。

find_bridges() 函数负责初始化统计信息和结果数据结构，并开始搜索。算法对每个连通分量执行一次深度优先搜索即可找到所有桥。由于每个节点仅访问一次，每条边最多检查两次（双向），算法复杂度为 |V| + |E|。

示例

图 11-9 展示了桥检测算法在一个 8 节点图上的运行示例。每个子图显示访问到圈出的节点后搜索的状态，DFSTreeStats 的 order 和 low 列表也显示其中。箭头表示已遍历的边，虚线表示搜索见过但未遍历的边，加粗灰色箭头为桥。

• 图 11-9(a) 显示搜索完成节点 6 后的状态，此时节点 0、1、2、3、7、6 已访问并设置了 preorder 索引，节点 4、5 尚未访问。节点 6 的 lowest 值最终确定，而节点 3 的 lowest 值尚未确定，因为其子树还未搜索完。
• 图 11-9(b) 显示搜索回溯到节点 7 并完成该节点，此时算法检查边 (7, 6) 是否为桥。由于 lowest[6] < order[6]，说明子树有另一条出路（通过节点 2），因此边不是桥。

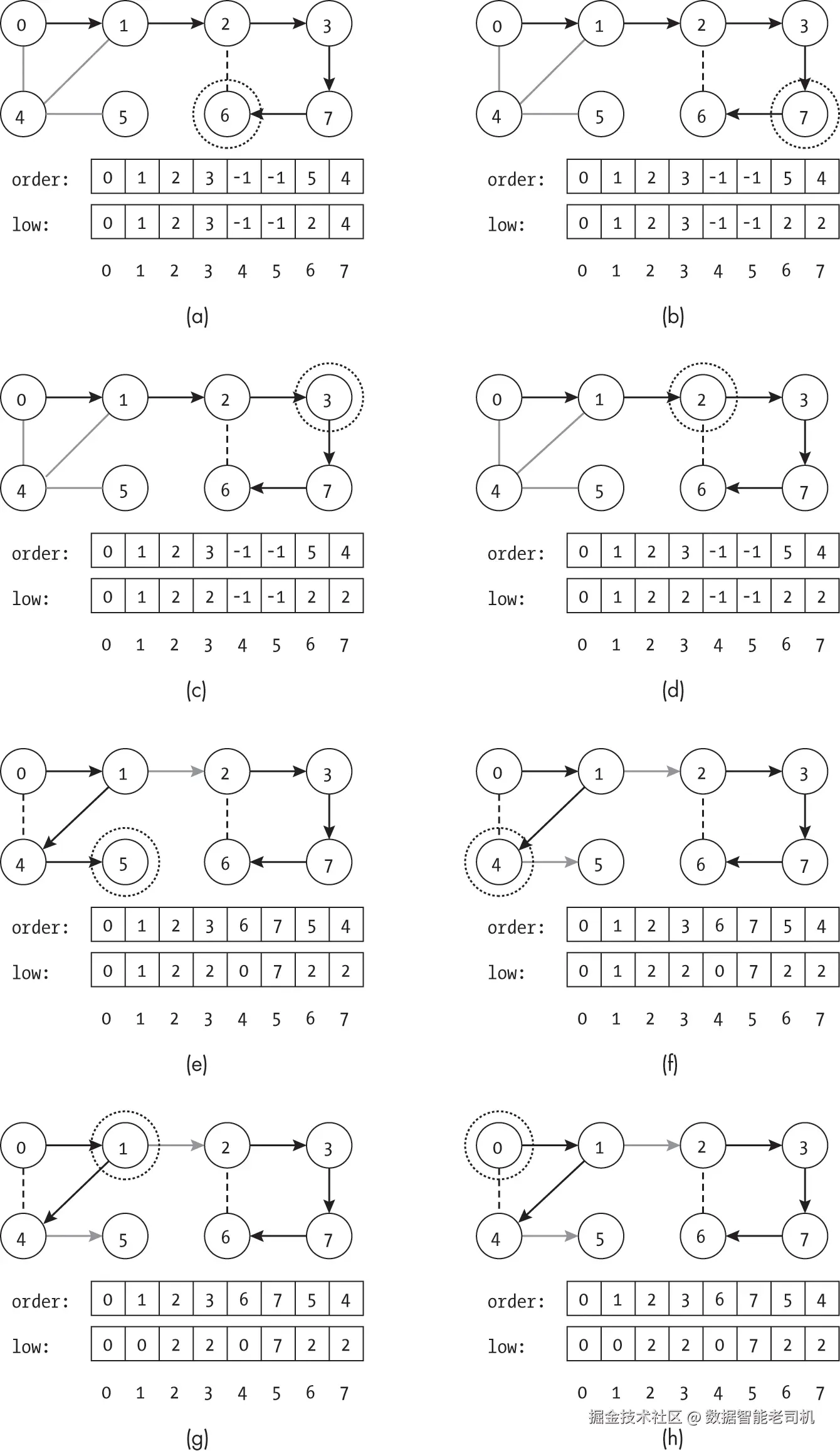
在图 11-9(e) 中，搜索找到了第一个桥。虽然对节点 1 的处理尚未完成，但节点 2 为根的子树已经被完全搜索。返回节点 2 后，算法发现 lowest[2] 等于 order[2]，表明边 (1, 2) 是进入或离开以节点 2 为根的子树的唯一路径。算法将 (1, 2) 加入桥列表，然后继续搜索节点 1 的其他子节点。在图 11-9(f) 中，完成以节点 5 为根的子树搜索后，算法发现边 (4, 5) 必定是另一条桥，因为移除该边会使节点 5 与网络断开。

为了形象化理解，可以想象我们的邪恶巫师在检查他新建的魔法迷宫。他先沿着迷宫走一圈，建立深度优先树，并用粉笔在墙上记录每个房间的 preorder 索引。每进入一个新房间，他递归探索未访问的邻居房间，同时探头检查已访问邻居房间墙上的标记。当访问"松动天花板房间"时，他可能会发现新的邻居------"丑陋地毯房间"，同时也发现一条回到之前访问过的"总是闷热房间"的通道。在整个过程中，他记录自进入每个房间以来见过的最低顺序索引。

回溯每条走廊后，巫师检查笔记，确定刚访问的房间是否有邻居房间的 preorder 索引小于走廊尽头房间（回溯时刚离开的房间）。当回溯经过他最喜欢的"奢华吊灯走廊"时，他实际上在问："是否存在其他通道让冒险者到达前方某个房间？还是他们必须经过'奢华吊灯走廊'？"如果没有其他路径，他就可以将"奢华吊灯走廊"标记为桥，高兴地知道冒险者总会看到这条装饰奢华的走廊，同时计划放置陷阱。

寻找关节点的算法

我们可以通过类似逻辑，将桥检测算法改造来识别关节点，只需关注每个子树的根节点而不是直接连接的边。我们寻找关节点的方法是：找出一个节点 u，使得其在深度优先搜索树中的所有子孙节点都没有指向 u 以上节点的邻居。来自子树外部的节点到 u 的某个子孙节点的边，就提供了绕过 u 的关键备用路径。

为了理解如何利用节点的子树来识别关节点，考虑图 11-10 中展示的两种情况。我们将深度优先搜索的子树映射到原始无向图中，用箭头表示，并标记每个节点的顺序索引。当前正在考虑的节点用阴影标出，虚线边界标记节点的子孙。

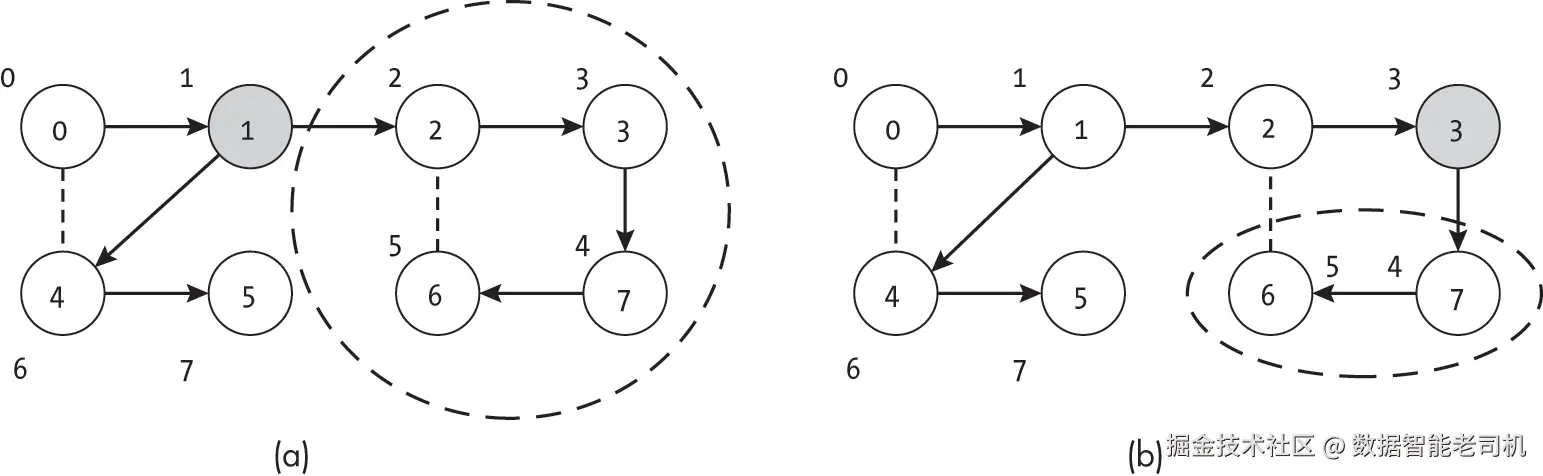
在图 11-10(a) 中，算法正在考虑节点 1 及其子孙节点 {2, 3, 6, 7}。移除节点 1 会将其子孙与图的其余部分隔离开来。相比之下，如图 11-10(b) 所示，节点 3 并不是关节点。该节点的子孙包括节点 6，而节点 6 有一条回到节点 2 的连接（节点 3 的子树之外）。边 (2, 6) 虽然不在深度优先搜索树中，但如果节点 3 被移除，它提供了一条到达节点 6 和 7 的备用路径。

这种逻辑适用于除根节点以外的所有节点。由于根节点没有祖先，我们不能用检查子树中回边的方式来判断。相反，我们必须关注根节点拥有多个子树的情况。如图 11-11 的示例图所示，根节点只有在图中存在移除根节点会导致断开的连通部分时，才会有多个子树。如果子树之间存在连接边，深度优先搜索会在返回根节点之前遍历该边。

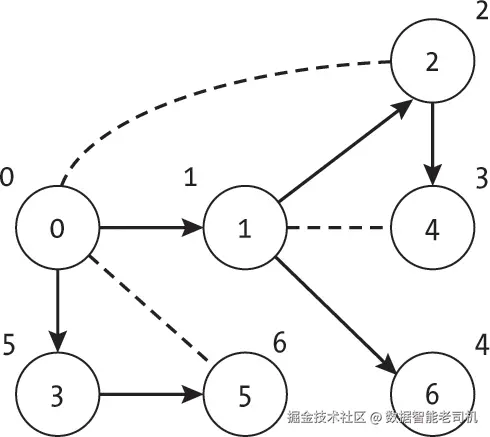
我们可以将针对根节点的特殊判断与桥检测算法中的下界跟踪结合起来，从而识别图中的关节点，如下列代码所示。

代码说明

与桥查找算法类似，我们用一次深度优先搜索实现关节点查找算法，同时完成搜索和识别。我们复用 DFSTreeStats 数据结构来跟踪和更新每个节点的父节点、序号以及可达的最小序号。

为了简化代码，我们将搜索分为两个函数。第一个函数处理非根节点，并执行递归探索：

def articulation_point_dfs(g: Graph, index: int, stats: DFSTreeStats,
                           results: set): 
  ❶ stats.set_order_index(index)
    for edge in g.nodes[index].get_edge_list():
        neighbor: int = edge.to_node
        if stats.order[neighbor] == -1:
            stats.parent[neighbor] = index
            articulation_point_dfs(g, neighbor, stats, results)
          ❷ stats.lowest[index] = min(stats.lowest[index],
                                      stats.lowest[neighbor])

          ❸ if stats.lowest[neighbor] >= stats.order[index]:
                results.add(index)

        elif neighbor != stats.parent[index]:
          ❹ stats.lowest[index] = min(stats.lowest[index],
                                      stats.order[neighbor])

递归函数 articulation_point_dfs() 执行算法的大部分工作。它首先设置当前节点的序号和初始下界 ❶，然后通过迭代每个邻居执行深度优先搜索，检查邻居是否已访问，如果没有则递归探索。

代码会跟踪子树中任意节点的邻居的最小序号。对于深度优先搜索树中的子树（之前未探索的节点），代码会基于整个子树邻居的最低序号更新下界 ❷。识别关节点的逻辑发生在对子树的递归探索完成之后：检查移除当前节点后，其子树是否被切断，通过判断子树中的任意节点是否有邻居在 DFS 树中位于当前节点之上 ❸。

对于不在 DFS 子树中的邻居（已探索节点）且不是当前节点的父节点，代码将节点的下界与邻居的序号进行比较 ❹。

根节点处理

对于根节点，我们增加额外逻辑来跟踪子树数量：

def articulation_point_root(g: Graph, root: int,
                            stats: DFSTreeStats, results: set): 
    stats.set_order_index(root)
    num_subtrees: int = 0

    for edge in g.nodes[root].get_edge_list():
        neighbor: int = edge.to_node
      ❶ if stats.order[neighbor] == -1:
            stats.parent[neighbor] = root
            articulation_point_dfs(g, neighbor, stats, results)
            num_subtrees += 1

  ❷ if num_subtrees >= 2:
        results.add(root)

articulation_point_root() 函数首先设置根节点的序号并初始化 num_subtrees 计数器。然后遍历每个邻居，检查是否已访问 ❶，如果未访问，则用 articulation_point_dfs() 递归探索。根节点是否为关节点不是通过下界逻辑判断，而是检查其是否有两个或更多子树 ❷。如果是，则将根节点加入结果集。

查找所有关节点

使用 articulation_point_root() 函数在图中每个连通分量上运行搜索即可找到所有关节点：

def find_articulation_points(g: Graph) -> set:
    stats: DFSTreeStats = DFSTreeStats(g.num_nodes)
    results: set = set()
    for index in range(g.num_nodes):
      ❶ if stats.order[index] == -1:
            articulation_point_root(g, index, stats, results)
    return results

find_articulation_points() 函数首先创建并初始化算法所需的数据结构。由于数据结构以节点索引为标识，且不同连通分量互不相交，因此可以使用同一 stats 和 results 对象处理所有连通分量。然后遍历每个节点，检查是否已被访问 ❶，若未访问则从该节点开始新的深度优先搜索，最后返回所有关节点列表。

示例

图 11-12 展示了算法查找关节点的示例。每个子图显示访问完带圈节点后的算法状态。若边是 DFS 树的一部分，用箭头表示；若不是，则用虚线表示。未探索的边为实心灰线，而已发现的关节点用阴影标出。

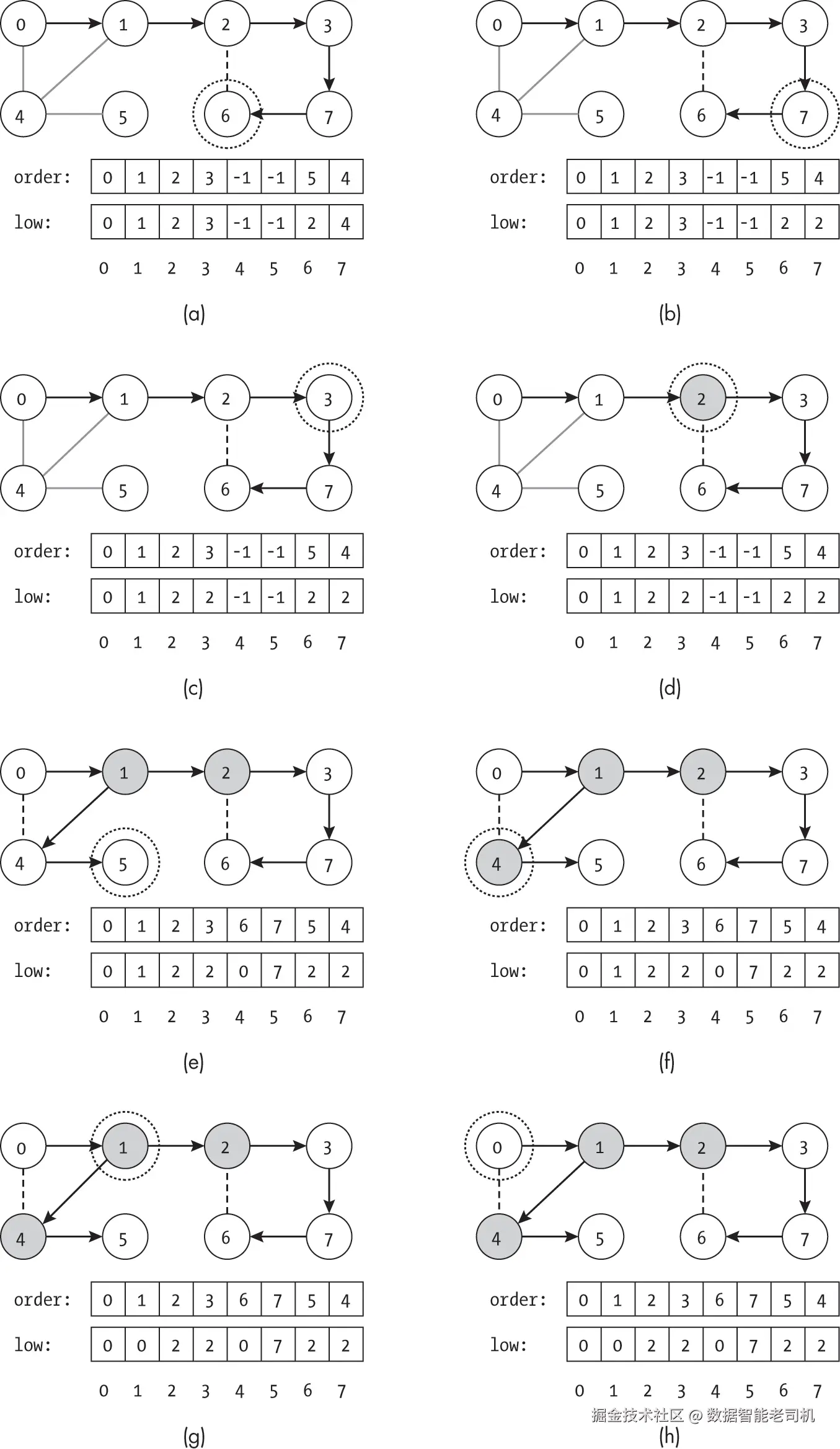
图 11-12 中展示的算法行为在大多数情况下与图 11-9 相同。节点的探索顺序以及每一步中 DFSTreeStats 的数值都是一致的。行为差异出现在图 11-12(d) 中检测到关节点的地方。以节点 3 为根的子树中任何邻居的最低序号为 2，即当前节点的序号。我们知道节点 2 至少有一个子树与其祖先没有连接，这意味着移除节点 2 会使该子树与图的其余部分断开。

图 11-12(e) 很有意思，因为尽管它显示的是完成节点 5 后的状态，算法已经将（尚未完成的）节点 1 标记为关节点，这是因为在检查每个子树后就进行了关节点测试。无论在探索节点 1 的其他后代时发生什么，我们都知道移除该节点会断开以节点 2 为根的子树。

图 11-12(h) 显示了算法的最后一步。此时，搜索已从 articulation_point_dfs() 函数返回，并正在测试根节点。此时不使用下界逻辑，而是检查根节点有多少子树，结果显示节点 0 只有一个深度优先搜索子树。搜索在返回节点 0 前通过节点 1 到达图中的所有节点，因此节点 0 不是关节点。

为什么这很重要

桥和关节点对于理解图的结构至关重要，包括其潜在的故障点和瓶颈。如前面的示例用例所示，这些特性可应用于各种现实问题，从为航空网络设计冗余路线，到构建终极魔法迷宫。

本章介绍的算法提供了识别这些结构元素的实用方法，通过深度优先搜索树和序号来判断哪些节点可以通过替代路径到达。这再次体现了简单深度优先搜索的强大与灵活，同时展示了通过增加诸如序号之类的信息可以深入理解图的整体结构。

下一章将进一步扩展关于连通性的讨论，这次考虑有向图及其相关概念------强连通分量。我们将介绍一种算法，它基于本章通过深度优先搜索收集统计信息的思路，来理解图的结构。