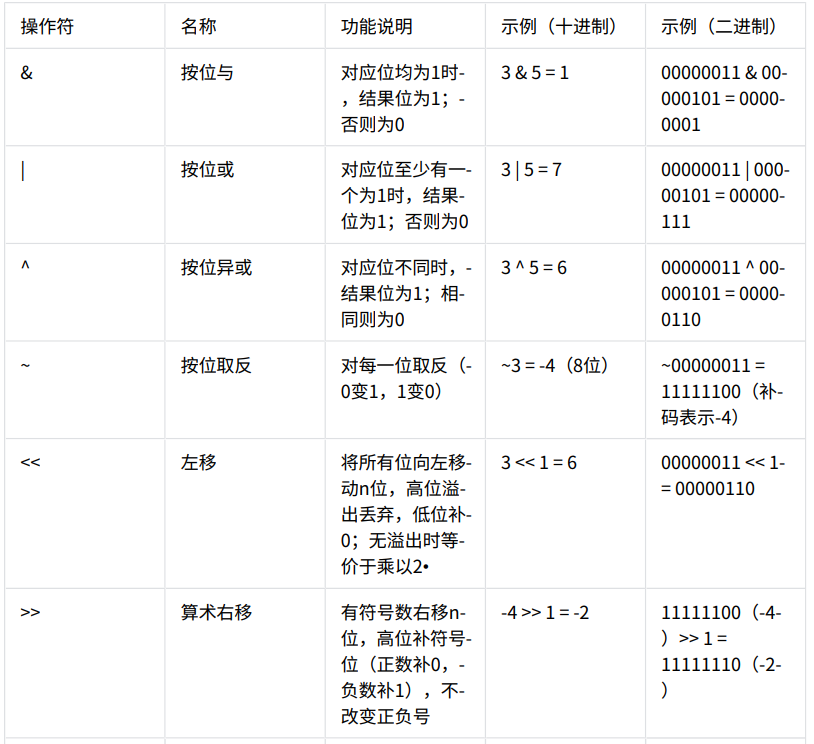
C++算法竞赛：位运算

喜欢吃燃面2025-08-18 8:17

**位运算**

必备知识

1.基础知识

2.注意事项

2.1位移操作

  • 左移（<<）和算术右移（>>）主要用于有符号整数，逻辑右移（>>>）多见于无符号整数操作（如 Java 中明确区分，C/C++无统一标准 ）。

2.2按位取反

  • 按位取反（~）结果依赖补码规则，对正数取反后结果为负数（如示例中 ~3 = -4 ）。

2.3位移注意事项

  • 位移操作中，"n"为移动的位数，需注意溢出问题（左移可能导致符号改变，右移可能因补位规则不同结果差异较大 ）。

这样梳理后，各知识点的逻辑和重点更突出，方便理解与记忆，若需结合代码示例进一步阐释，可补充说明 。

一.判断奇数偶数

1.题目

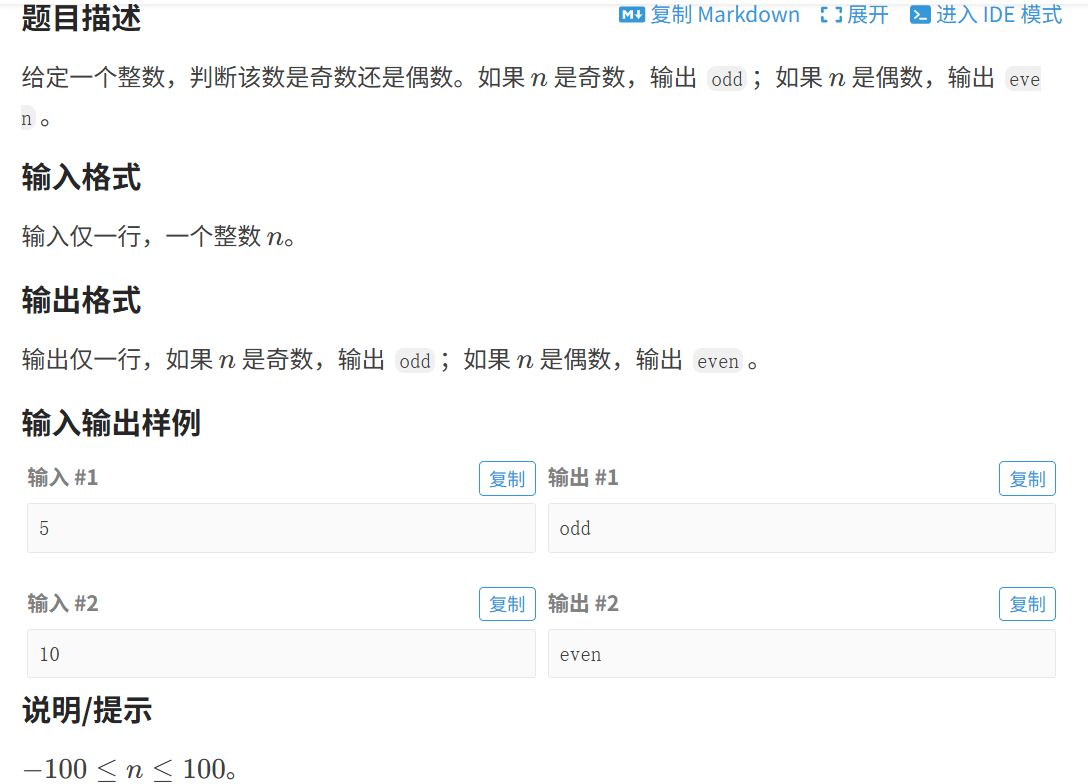
2.解题思路

这是利用按位与（&）运算判断整数奇偶性的原理

2.1核心逻辑：二进制最低位决定奇偶

整数在计算机中以二进制存储，最低位（最右侧）是 0 则为偶数，是 1 则为奇数 。

按位与（&）运算规则：两个二进制位都为 1 时结果才是 1，否则为 0 。用 x & 1 可提取 x 的最低位，通过判断结果是否为 0 或 1，就能区分奇偶。

2.2偶数判断（以 x=2、4、6、8 为例 ）

  1. 二进制特征 ：这些偶数的二进制最低位都是 0（如 2 是 0010 、6 是 0110 ）。
  2. 按位与运算 ：执行 x & 1 时，相当于用 x 的二进制和 0001 做按位与。

    • 以 x=6（二进制 0110 ）为例：

      复制代码 
      0110
& 0001
------
0000

      结果为 0 ，即 (x & 1) == 0 ，说明 x 是偶数。

2.3奇数判断（以 x=1、3、5、7、9 为例 ）

  1. 二进制特征 ：这些奇数的二进制最低位都是 1（如 1 是 0001 、5 是 0101 ）。
  2. 按位与运算 ：执行 x & 1 时，用 x 的二进制和 0001 做按位与。

    • 以 x=5（二进制 0101 ）为例：

      复制代码 
      0101
& 0001
------
0001

      结果为 1 ，即 (x & 1) == 1 ，说明 x 是奇数。

2.4总结

通过 x & 1 提取整数 x 的二进制最低位，根据结果判断奇偶：

  • 若 x & 1 == 0 → x 是偶数；
  • 若 x & 1 == 1 → x 是奇数 。
    这种方式比取余（%）判断奇偶更高效，因为位运算直接操作二进制，底层执行更快。

参考代码

cpp 复制代码 
#include<iostream>
using namespace std;

int main()
{
    int n;cin>>n;
    if(n&1)cout<<"odd";
    else cout<<"even";
return 0;
}

二.颠倒二进制为

1.题目


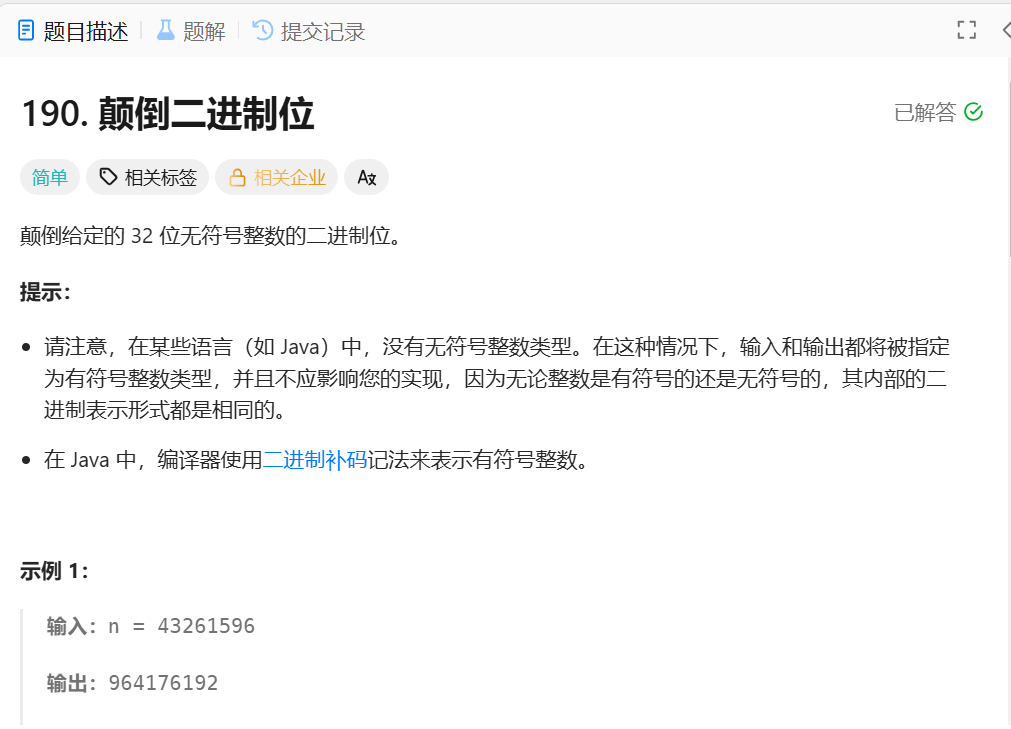
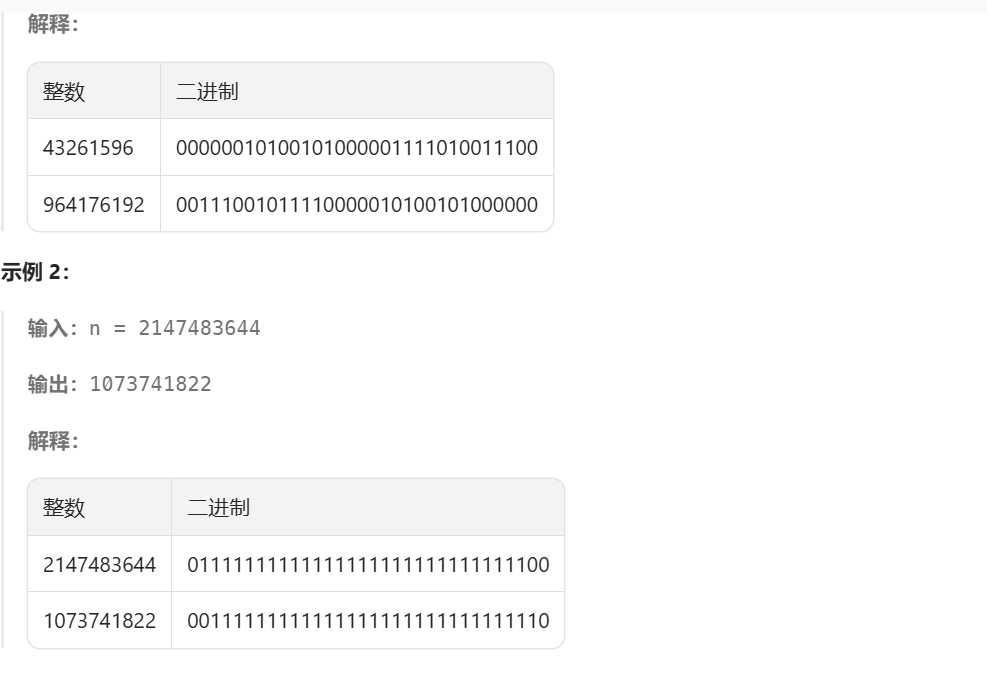
2.解题思路

LeetCode 190 题「颠倒二进制位」

核心目标

把一个 32 位无符号整数 n 的二进制位 完全颠倒 ，比如原二进制是 b₃₁ b₃₀ ... b₁ b₀（b₃₁ 是最高位，b₀ 是最低位 ），颠倒后变成 b₀ b₁ ... b₃₀ b₃₁。

手动模拟步骤（逐位处理）

可以把这个过程想象成**"拆位 + 反向拼接"**，分 32 步完成（因为是 32 位），每一步处理 1 个二进制位：

1. 初始化结果

准备一个"容器" ret，用来存颠倒后的二进制位 ，初始值为 0（相当于二进制全 0）。

2. 逐位处理原数 n

循环 32 次（对应 32 个二进制位），每次做 3 件事：

  • ① 取 n 的当前最低位 ：

    用 n & 1 提取 n 的**最右侧（最低位）**的值，记为 b（b 是 0 或 1）。

    比如 n 是 1010（二进制），第一次 n & 1 得到 0（最低位是 0）；第二次 n 右移后变成 101，n & 1 得到 1（新的最低位是 1）......

  • ② 把 b 放到 ret 的"高位方向"：

    • 先把 ret 左移 1 位 （ret <<= 1）：相当于给新位腾空间，比如 ret 原本是 101，左移后变成 1010，最低位空出 0。
    • 再用 ret |= b：把 b 放到 ret 的最低位（此时因为左移，这个"最低位"实际对应颠倒后的高位方向）。

  • ③ 处理 n 的下一位 ：

    把 n 右移 1 位 （n >>= 1），让原本的"次低位"变成新的"最低位"，供下一轮处理。

3. 循环结束，得到结果

32 次循环后，ret 里就存好了所有位颠倒后的二进制值 ，直接返回 ret 即可。

结合图示理解

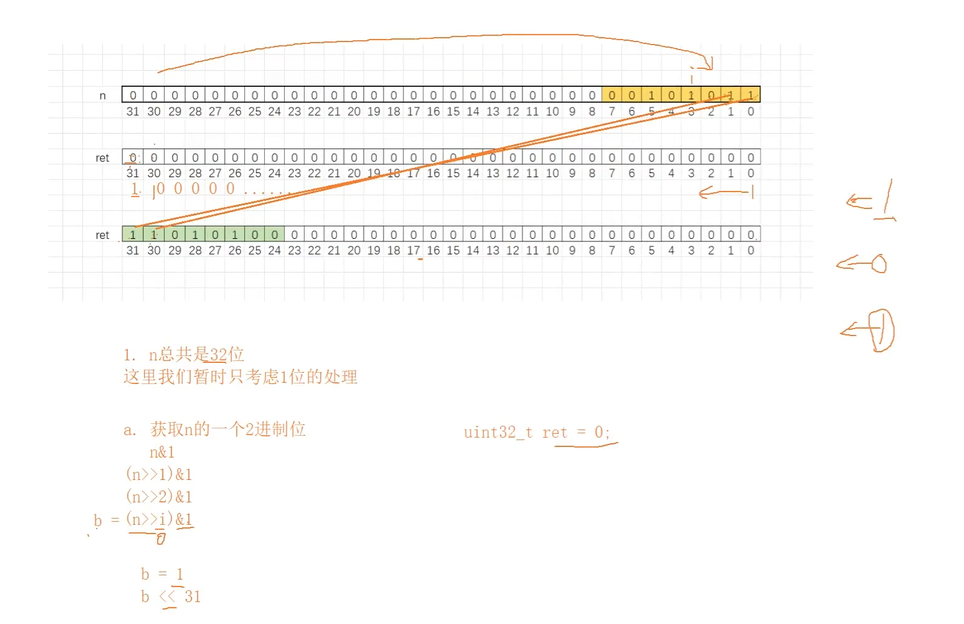
  • 最上面的 n 是原始 32 位二进制，右侧是低位（0 位）、左侧是高位（31 位）。
  • 中间的 ret 初始全 0，每次左移 + 存新位，相当于从 n 的低位开始，反向拼接到 ret 的高位。
  • 最终 ret 的二进制位就是 n 的"镜像"，完成颠倒。

关键逻辑总结

本质是**"逐位拆解、反向组装"**：

  • 从 n 的最低位开始，依次取出每一位。
  • 把取出的位反向"填"到 ret 的低位（靠左移实现"高位方向填充"）。
  • 严格循环 32 次，确保 32 位全部处理（包括高位的 0，否则会漏掉补 0 导致结果错误）。

清晰理解颠倒二进制位的逻辑：就是把原数的二进制位从"最右到最左"拆出来，再"从最左到最右"拼回去，实现完全颠倒 。

3.参考代码

cpp 复制代码 
class Solution {
public:
    int reverseBits(int n) {
        int ret=0;
  for(int i=0;i<32;i++)
  {
    if((n>>i)&1)
    {
        int b=((n>>i)&1);
        b<<=(31-i);
        ret|=b;
    }
  }
  return ret;
    }
};

三.数字的补数

1.题目

2.解题思路

题目本质

对 num 的有效二进制位（不含前导 0） 进行按位取反 （0 变 1，1 变 0），再转十进制。

比如：

  • num = 5（二进制 101）→ 取反后 010 → 十进制 2。
  • num = 1（二进制 1）→ 取反后 0 → 十进制 0。

解题步骤（逐位处理）

核心逻辑是 "拆位 → 取反 → 组装"，分 3 步：

1. 初始化结果

定义 ret = 0，用来存取反后的二进制值（最终转十进制）。

2. 逐位处理 num 的二进制位

循环处理 num 的每一位，直到 num 变为 0（处理完所有有效位）：

  • ① 拆出当前位 ：

    用 b = num & 1 提取 num 的最低位 （比如 num = 5 是 101，第一次 b = 1；右移后 num = 10，第二次 b = 0......）。

  • ② 对当前位取反 ：

    取反逻辑：b ^= 1（0 变 1，1 变 0），或者用 if (b == 0) b = 1; else b = 0;（对应你草稿里的 if 逻辑）。

  • ③ 把取反后的位"拼"到 ret：

    • 先把 ret 左移 1 位 （ret <<= 1）：给新位腾空间，比如 ret 原本是 10，左移后变成 100，最低位空出 0。
    • 再用 ret |= b：把取反后的 b 放到 ret 的最低位。

  • ④ 处理下一位 ：

    把 num 右移 1 位 （num >>= 1），让原本的"次低位"变成新的"最低位"，供下一轮处理。

3. 循环结束，得到结果

当 num 右移到 0 时，所有有效二进制位 都已处理完毕，ret 里存的就是取反后的二进制值 ，直接返回 ret 即可。

结合图示理解

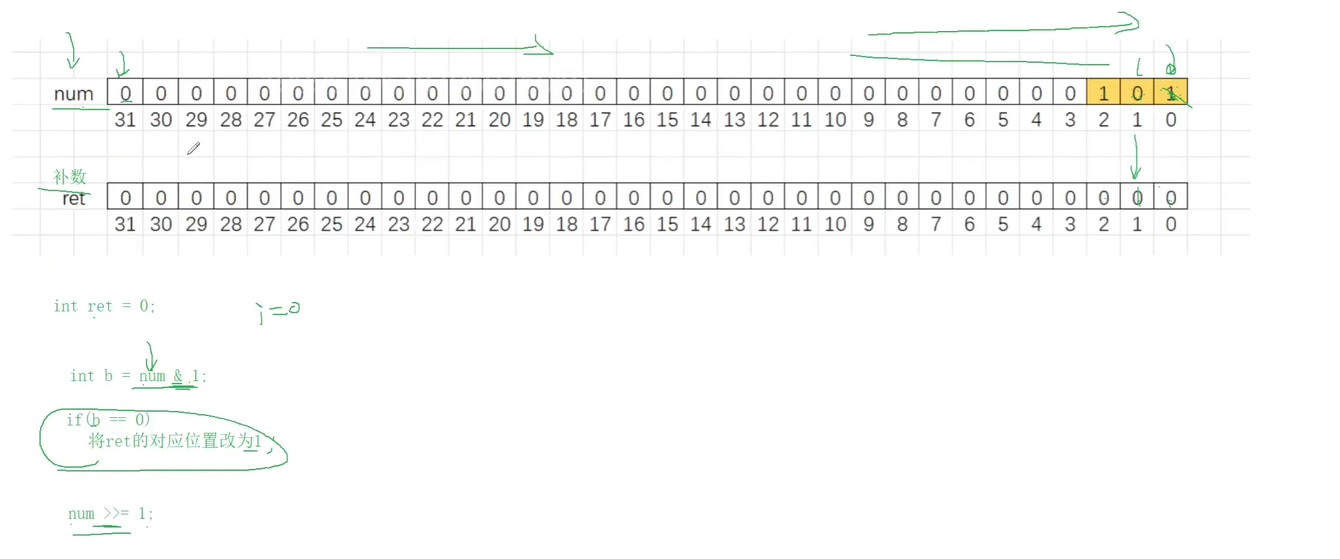
  • 最上面的 num 是二进制，右侧是低位（0 位）、左侧是高位。
  • 中间的 ret 初始全 0，每次左移 + 存新位，相当于从 num 的低位开始，取反后反向拼接到 ret。
  • 比如 num 最低位是 1，取反后变成 0，拼到 ret；下一位是 0，取反后变成 1，拼到 ret...... 最终 ret 就是取反后的结果。

关键逻辑总结

本质是 "逐位拆、取反、反向组装"：

  • 只处理 num 的有效二进制位 （不含前导 0），通过 num >>= 1 自动跳过前导 0（因为 num 为 0 时循环结束）。
  • 取反用位运算 （^1 或条件判断），拼接用左移 + 或运算，高效且直观。

代码草稿对应逻辑

草稿里的 if (b == 0) 将 ret 的对应位置改为 1，实际就是 ret <<= 1; ret |= 1;（因为 b == 0 时取反后是 1）；如果 b == 1，则是 ret <<= 1; ret |= 0;（等价于不操作，因为 |= 0 不改变值，但逻辑上需要处理）。

3.参考代码

cpp 复制代码 
class Solution {
public:
    int findComplement(int num) {
        int i = 0, ret = 0;
while (num)
{
    if ((num & 1) == 0)
        ret |= (1 << i);
    num >>= 1;
    i++;
}
return ret;
    }
};

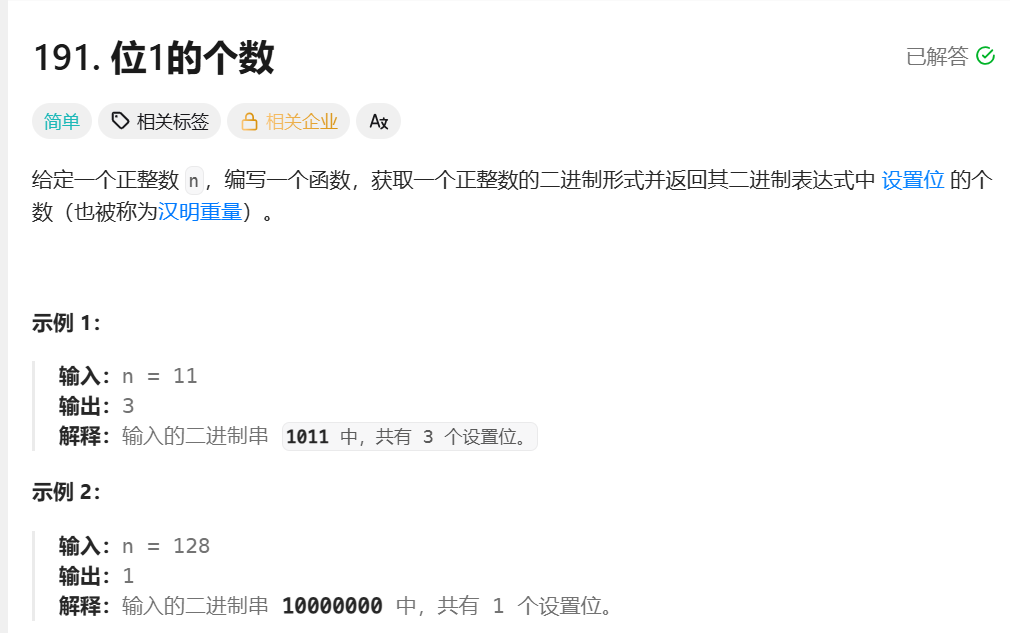
四.位1的个数

1.题目

2.解题思路

方法一：逐位"扒开看"

  1. 核心想法 ：

    整数在计算机里是 32 位二进制 存的（比如 int 类型），咱从最右边第 0 位，到最左边第 31 位，一位一位检查 ，看是不是 1。

  2. 具体咋做：

    • 准备一个计数器，记录 1 的个数，初始为 0。
    • 循环 32 次（因为要查 32 位），每次干这两件事：
      • 用 1 << i 造一个"掩码"：比如 i=0 时，1 << 0 就是 000...0001（只有第 0 位是 1）；i=1 时，就是 000...0010（只有第 1 位是 1）......以此类推。
      • 拿这个掩码和原数 n 做 按位与（&） ：如果结果不是 0，说明 n 的第 i 位是 1，计数器 +1；要是结果是 0，说明这一位是 0，跳过。
    • 循环结束，计数器就是 1 的总个数。

参考代码

cpp 复制代码 
int hammingWeight(int n) {
    int cnt = 0;
    for (int i = 0; i < 32; i++)
    {
        if (n & (1 << i))
            cnt++;
    }
    return cnt;
}

方法二：每次"干掉一个 1"

  1. 核心想法 ：

    利用一个 二进制小技巧 ：n & (n - 1) 会 把 n 最右边的 1 变成 0 。比如：

    • n = 1010（二进制），n-1 = 1001，n & (n-1) = 1000 → 最右边的 1（第 1 位）被干掉了。
    • 每次这么干，就能逐个消灭 1 ，消灭一次就计数，直到 n 变成 0（所有 1 都消灭完）。

  2. 具体咋做：

    • 准备计数器，初始为 0。
    • 只要 n 还不是 0，就循环：
      • 把 n 变成 n & (n - 1)（干掉最右边的 1）。
      • 计数器 +1（因为刚干掉了一个 1）。
    • 循环结束，计数器就是 1 的总个数。

参考代码

cpp 复制代码 
nt hammingWeight(int n) {
    int cnt = 0;
    while (n)
    {
        n = n & (n - 1);
        cnt++;
    }
    return cnt;
}

两种方法对比

  • 方法一：稳扎稳打，把 32 位全查一遍，适合刚学二进制，想"看明白每一位"的场景。
  • 方法二 ：更聪明，循环次数等于 1 的个数（比如 n 有 3 个 1，就循环 3 次），效率更高，适合想"偷懒少循环"的情况。

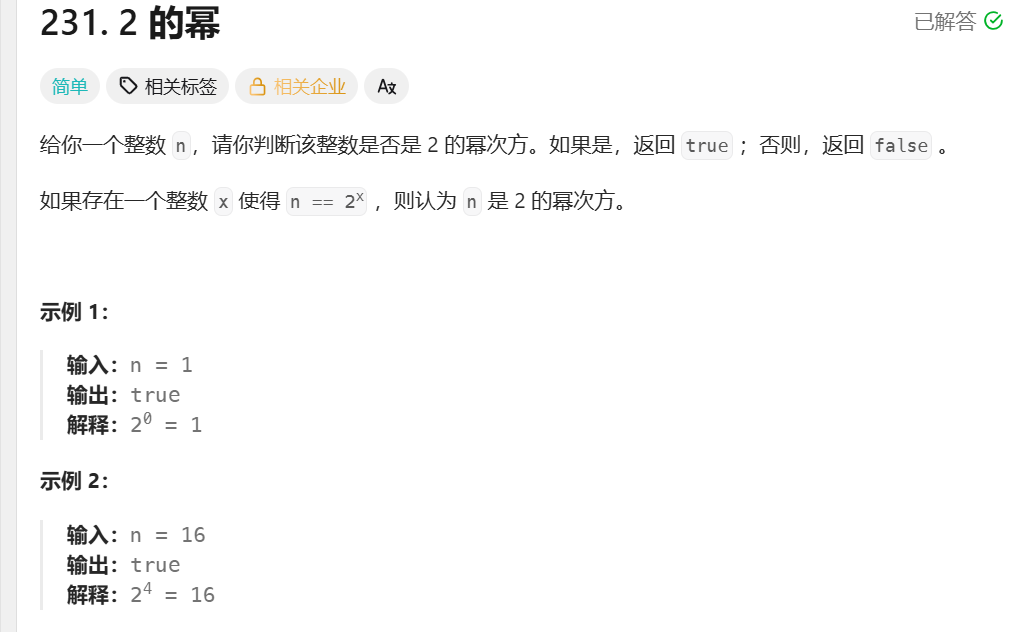
五.2的幂

1.题目

2.解题思路

方法一："找唯一的 1 在哪里"

  1. 核心观察 ：

    2 的幂的二进制有个特点：只有 1 个 1 。比如：

    • 2^0 = 1 → 二进制 1（1 个 1）
    • 2^1 = 2 → 二进制 10（1 个 1）
    • 2^2 = 4 → 二进制 100（1 个 1）......
      所以，只要找到 n 二进制里 唯一的 1 所在的位置 ，再验证 n 是否等于 2 的该次方，就能判断。

  2. 具体思路：

    • 准备一个计数器 cnt，遍历 n 的 32 位（int 是 32 位），用 (1 << i) 生成掩码，和 n 做 按位与（&） 。
    • 一旦发现某一位是 1（结果非 0），就把当前的 i 记到 cnt 里（因为这就是唯一 1 的位置）。
    • 最后验证：n 是否等于 2^cnt（比如 n=8，找到 1 在第 3 位，2^3=8，就符合）。

参考代码

cpp 复制代码 
bool isPowerOfTwo(int n) {
    int tmp = n, cnt = 0;
    for (int i = 0; i < 32; i++)
    {
        if (n & (1 << i))
            cnt = i;
    }
    return n == pow(2, cnt);
}

方法二："把唯一的 1 干掉，看是否变 0"

  1. 核心观察 ：

    延续"只有 1 个 1"的特点，用 n & (n - 1) 这个操作：它会 把 n 最右边的 1 变成 0 。

    比如 n=8（1000），n-1=7（0111），n & (n-1) = 0 → 唯一的 1 被干掉，结果直接变 0 。

    反过来想：如果 n 是 2 的幂，n & (n - 1) 结果一定是 0 ；如果不是，结果不会是 0（比如 n=6 是 110，n-1=5 是 101，n & (n-1)=100≠0 ）。

  2. 具体思路：

    • 先判断 n ≥ 1（因为 2 的幂是正整数，n=0 或负数直接不满足）。
    • 再判断 n & (n - 1) == 0 ：如果满足，说明 n 二进制只有 1 个 1，是 2 的幂；否则不是。

参考代码

cpp 复制代码 
bool isPowerOfTwo(int n) {
    return (n >= 1) && ((n & (n - 1)) == 0);
}

方法三："用补码特性，锁定唯一的 1"（isPowerOfTwo03）

  1. 核心观察 ：

    利用 补码（-n 的表示） 特性：n & -n 的结果，是 n 二进制里 最右边的 1 及右边的 0 组成的数 。

    比如：

    • n=8（1000），-n 是补码（二进制 ...11111000 ），n & -n = 1000（即 8 本身）。
    • 如果 n 是 2 的幂（只有 1 个 1），那么 n & -n 的结果 一定等于 n 本身 （因为唯一的 1 就是最右边的 1 ）。

  2. 具体思路：

    • 同样先判断 n ≥ 1（排除 0 和负数）。
    • 再判断 n == (n & -n) ：满足则说明 n 只有 1 个 1，是 2 的幂；否则不是。

参考带码

cpp 复制代码 
bool isPowerOfTwo(int n) {
    return (n >=1) && n == (n & -n);
}

三种方法对比

  • 方法一 ：适合理解"找 1 的位置"，但需要额外计算 2^cnt 验证，稍繁琐。
  • 方法二 ：利用 n & (n-1) 经典技巧，逻辑简洁，效率高，最常用。
  • 方法三：借助补码特性，更巧妙，但需要理解补码概念，适合想拓展思路的同学。

六.丢失的数字

1.题目

2.解题思路

方法一：完整集对比法

核心原理

基于集合的"完整性校验"思想。已知题目中数组应包含区间 [0, n]（n 为数组长度）的全部整数，但缺失其中一个。通过构造完整的 [0, n] 集合，与输入数组逐一比对，筛选出未匹配的元素，即为丢失数字。

推导过程
  1. 构造完整序列 ：根据数组长度 n，生成包含 0 到 n 所有整数的完整序列（如数组长度为 3 时，完整序列为 [0, 1, 2, 3] ）。
  2. 逐元素匹配校验 ：遍历完整序列的每个元素，通过嵌套遍历输入数组，利用异或运算（两数异或结果为 0 时，表明两数相等）判断该元素是否存在于输入数组中。
  3. 定位缺失值：若完整序列中某元素在输入数组遍历后仍未匹配到（标记为未找到），则该元素即为丢失的数字。

参考代码

cpp 复制代码 
int missingNumber(vector<int>& nums) {
    size_t n = nums.size();
    vector<int> arr;
    // 创建包含0~n的完整数组
    for (int i = 0; i <= n; i++) {  // 注意是 <=n，因为nums.size()是n，缺失的是0~n中的一个
        arr.push_back(i);
    }

    // 遍历完整数组，检查每个元素是否在nums中
    for (size_t j = 0; j < arr.size(); j++) {
        bool found = false;  // 标记当前arr[j]是否在nums中找到
        for (size_t i = 0; i < nums.size(); i++) {
            if ((arr[j] ^ nums[i]) == 0) {  // 异或为0表示两数相等
                found = true;
                break;  // 找到后退出内层循环
            }
        }
        // 如果遍历完nums都没找到，说明arr[j]是缺失的数字
        if (!found) {
            return arr[j];
        }
    }
}

二、方法二：异或消元法

核心原理

利用异或运算的特性：

  • 相同整数异或结果为 0（如 a ^ a = 0 ）；
  • 任意整数与 0 异或结果为其本身（如 a ^ 0 = a ）；
  • 异或满足交换律与结合律（如 a ^ b ^ c = a ^ c ^ b ）。

基于此，若将"完整区间 [0, n] 的所有整数"与"输入数组的所有元素"进行异或运算，成对出现的整数会因异或抵消为 0，最终剩余的结果即为仅出现一次（缺失）的数字。

推导过程
  1. 补全完整区间 ：由于输入数组长度为 n，完整区间应为 [0, n] 。初始化结果变量为 n（补全完整区间的右端点，保证参与异或的元素覆盖 0 到 n ）。
  2. 遍历异或消元 ：遍历输入数组，将当前下标 i （对应完整区间的 0 到 n-1 ）与数组元素 nums[i] 依次异或到结果变量中。
  3. 输出缺失值：遍历结束后，结果变量即为丢失的数字（因其他成对元素已异或抵消，仅缺失值未被抵消 ）。

参考代码

cpp 复制代码 
int missingNumber03(vector<int>& nums) {
    int sz = int(nums.size());  
    int ret = sz;               // 初始化结果为n（补全完整区间的最后一个元素）
    
    // 遍历数组，将下标i（对应0~n-1）与数组元素nums[i]依次异或到结果中
    for (int i = 0; i < sz; i++)
    {
        // 等价于 ret = ret ^ i ^ nums[i]
        // 作用：通过异或消去完整区间与数组中都存在的数字
        ret ^= i ^ nums[i];
    }
    
    // 循环结束后，ret中保留的就是唯一未被消去的丢失数字
    return ret;
}

三、方法三：数学求和法（对应 missingNumber04）

核心原理

利用等差数列求和公式 ：完整区间 [0, n] 的整数和可通过公式 total = n * (n + 1) / 2 计算。由于输入数组是完整区间丢失一个数字后的结果，因此完整区间和 与输入数组和的差值，即为丢失的数字。

推导过程
  1. 计算完整区间和 ：通过等差数列求和公式，计算 0 到 n 的理论总和 total 。
  2. 计算输入数组和 ：遍历输入数组，累加所有元素得到实际和 sum 。
  3. 求差值得结果 ：丢失的数字 = 完整区间和 total - 输入数组和 sum ，直接返回该差值即可。

参考代码

cpp 复制代码 
// 用数学求和公式：缺失值 = 0~n的和 - nums元素的和
int missingNumber04(vector<int>& nums) {
    int n = nums.size();
    int total = n * (n + 1) / 2;  // 0~n的总和
    int sum = 0;
    for (int num : nums) {
        sum += num;
    }
    return total - sum;
}

三种方法对比

  • 暴力枚举法（方法一）：逻辑简单直接，通过构建完整序列 + 嵌套遍历比对找缺失值，但嵌套循环让效率低（时间复杂度 (O(n^2)) ），适合理解基础思路，数据量大时不推荐。
  • 异或消元法（方法二） ：利用异或"相同数抵消、留唯一数" 的特性，遍历一次即可（时间复杂度 (O(n)) ，空间 (O(1)) ），效率高、无额外空间消耗，是位运算技巧的典型应用，推荐日常解题优先用。
  • 数学求和法（方法三） ：依托等差数列求和公式，用"完整和 - 数组和"快速算缺失值，思路极简、计算成本低（时间 (O(n)) ），适合追求数学推导、想快速出结果的场景。

实际用哪种？数据规模小、想直观实现选暴力；追求高效/空间优化选异或；偏好数学思维、场景简单直接选求和，根据题目数据量和性能需求灵活挑！

相关推荐
tanyongxi6632 分钟前
C++ 特殊类设计与单例模式解析
java·开发语言·数据结构·c++·算法·单例模式
qq_5139704433 分钟前
力扣 hot100 Day76
算法·leetcode·职场和发展
遗憾皆是温柔34 分钟前
24. 什么是不可变对象，好处是什么
java·开发语言·面试·学习方法
fqbqrr1 小时前
2508C++,支持rdma通信的高性能rpc库
c++·rpc
wearegogog1231 小时前
C语言中的输入输出函数：构建程序交互的基石
c语言·开发语言·交互
Fine姐1 小时前
The Network Link Layer: 无线传感器中Delay Tolerant Networks – DTNs 延迟容忍网络
开发语言·网络·php·硬件架构
Moshow郑锴1 小时前
机器学习相关算法：回溯算法 贪心算法 回归算法(线性回归) 算法超参数 多项式时间 朴素贝叶斯分类算法
算法·机器学习·回归
HAPPY酷1 小时前
给纯小白的Python操作 PDF 笔记
开发语言·python·pdf
rannn_1111 小时前
【MySQL学习|黑马笔记|Day7】触发器和锁（全局锁、表级锁、行级锁、）
笔记·后端·学习·mysql
liulilittle1 小时前
BFS寻路算法解析与实现
开发语言·c++·算法·宽度优先·寻路算法·寻路
热门推荐
01UV安装并设置国内源02Qwen3-Coder 快速上手教程 | Qwen Code + Claude Code03KGG转MP3工具|非KGM文件|解密音频04【2025.08.06最新版】Android Studio下载、安装及配置记录（自动下载sdk）05蜘蛛磁力 搜索引擎大全，如何使用蜘蛛磁力查找磁力链接062025最新国内服务器可用docker源仓库地址大全（2025年8月更新）07TRAE 规则（Rules）配置指南：个人习惯、团队规范与最佳实践08NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南09阿里开源首个图像生成基础模型——Qwen-Image本地部署教程，超强中文渲染能力刷新SOTA！10TRAE Rules 实践：为项目配置 6A 工作流