二叉树
二叉树是非线性数据结构的一种,由节点组成,非空二叉树包含一个根节点和左右子树,左右子树也都是二叉树。
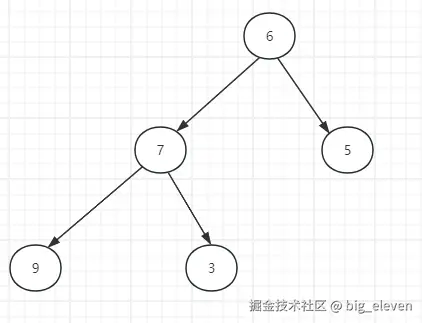
名词解释:
- 节点:包含数据元素及指向子节点的引用(指针);
- 根节点:二叉树的起始节点,无父节点;
- 叶子节点:无左、右子节点的节点(度为 0);
- 节点的度:节点拥有的子节点数量(0、1 或 2);
- 树的深度(高度):从根节点到最深叶子节点的路径长度(根节点深度为 1,空树深度为 0);
- 节点的层次:根节点为第 1 层,其子节点为第 2 层,以此类推;
- 祖先 / 后代:从根节点到某节点的路径上的所有节点为该节点的祖先;某节点的所有子树节点为其后代。
代码实现二叉树
java
public class BinaryTree<T> {
// 二叉树节点类
public static class TreeNode<T> {
T data; // 节点数据
TreeNode<T> left; // 左子节点
TreeNode<T> right; // 右子节点
public TreeNode(T data) {
this.data = data;
this.left = null;
this.right = null;
}
public TreeNode(T data, TreeNode<T> left, TreeNode<T> right) {
this.data = data;
this.left = left;
this.right = right;
}
}
protected TreeNode<T> root; // 根节点
// 构造空树
public BinaryTree() {
root = null;
}
// 根据根节点构造树
public BinaryTree(TreeNode<T> root) {
this.root = root;
}
// 判断树是否为空
public boolean isEmpty() {
return root == null;
}
// 获取树的高度
public int height() {
return height(root);
}
// 递归计算树的高度
private int height(TreeNode<T> node) {
if (node == null) {
return 0;
}
// 树的高度 = 1 + 左子树高度和右子树高度的最大值
int leftHeight = height(node.left);
int rightHeight = height(node.right);
return Math.max(leftHeight, rightHeight) + 1;
}
// 获取树的节点数
public int size() {
return size(root);
}
// 递归计算节点数
private int size(TreeNode<T> node) {
if (node == null) {
return 0;
}
// 总节点数 = 1(当前节点) + 左子树节点数 + 右子树节点数
return 1 + size(node.left) + size(node.right);
}
// 前序遍历(根 -> 左 -> 右)
public void preOrder() {
preOrder(root);
System.out.println();
}
private void preOrder(TreeNode<T> node) {
if (node != null) {
System.out.print(node.data + " "); // 访问根节点
preOrder(node.left); // 遍历左子树
preOrder(node.right); // 遍历右子树
}
}
// 中序遍历(左 -> 根 -> 右)
public void inOrder() {
inOrder(root);
System.out.println();
}
private void inOrder(TreeNode<T> node) {
if (node != null) {
inOrder(node.left); // 遍历左子树
System.out.print(node.data + " "); // 访问根节点
inOrder(node.right); // 遍历右子树
}
}
// 后序遍历(左 -> 右 -> 根)
public void postOrder() {
postOrder(root);
System.out.println();
}
private void postOrder(TreeNode<T> node) {
if (node != null) {
postOrder(node.left); // 遍历左子树
postOrder(node.right); // 遍历右子树
System.out.print(node.data + " "); // 访问根节点
}
}
// 层序遍历(按层次从上到下,从左到右)
public void levelOrder() {
if (root == null) {
return;
}
// 使用队列实现层序遍历
java.util.Queue<TreeNode<T>> queue = new java.util.LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode<T> node = queue.poll();
System.out.print(node.data + " ");
// 左子节点入队
if (node.left != null) {
queue.offer(node.left);
}
// 右子节点入队
if (node.right != null) {
queue.offer(node.right);
}
}
System.out.println();
}
// 测试方法
public static void main(String[] args) {
// 构建一棵示例二叉树:
// 1
// / \
// 2 3
// / \ \
// 4 5 6
TreeNode<Integer> node4 = new TreeNode<>(4);
TreeNode<Integer> node5 = new TreeNode<>(5);
TreeNode<Integer> node6 = new TreeNode<>(6);
TreeNode<Integer> node2 = new TreeNode<>(2, node4, node5);
TreeNode<Integer> node3 = new TreeNode<>(3, null, node6);
TreeNode<Integer> node1 = new TreeNode<>(1, node2, node3);
BinaryTree<Integer> tree = new BinaryTree<>(node1);
System.out.println("树的高度:" + tree.height()); // 输出:3
System.out.println("树的节点数:" + tree.size()); // 输出:6
System.out.print("前序遍历:");
tree.preOrder(); // 输出:1 2 4 5 3 6
System.out.print("中序遍历:");
tree.inOrder(); // 输出:4 2 5 1 3 6
System.out.print("后序遍历:");
tree.postOrder(); // 输出:4 5 2 6 3 1
System.out.print("层序遍历:");
tree.levelOrder();// 输出:1 2 3 4 5 6
}
}重要特点
-
第i层最多节点数:第i层((i > 1))最多有==2^(i-1)==个节点。
例:第 1 层最多 1 个(根节点),第 2 层最多 2 个,第 3 层最多 4 个,以此类推。
-
深度为k的二叉树最多节点数:总节点数==最多为2^k - 1==(满二叉树的情况)。
例:深度为 3 的满二叉树最多有(2^3 - 1 = 7)个节点。
-
节点数与度的关系:若叶子节点数为(n_0),度为 2 的节点数为(n_2),则(n_0 = n_2 + 1)。 推导:总节点数(n = n_0 + n_1 + n_2)((n_1)为度为 1 的节点数),总边数(n-1 = n_1 + 2n_2),联立得(n_0 = n_2 + 1)。
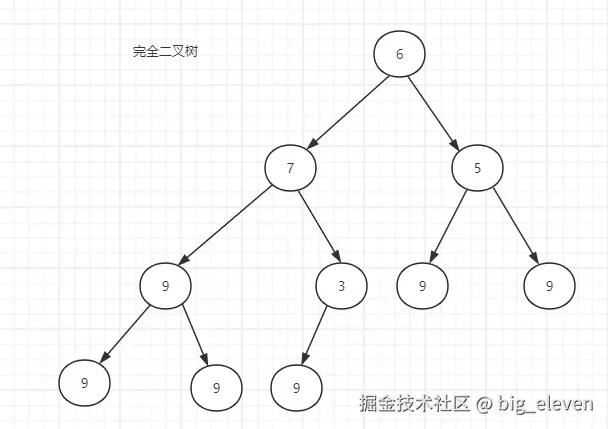
完全二叉树
假设一个二叉树由h层,那么如果从1 ~~ h-1 层的节点数都达到了最大的个数,并且第h层的节点是从左往右依次分布的,中间没有空缺,就是完全二叉树。

以下这个就不是一个完全二叉树
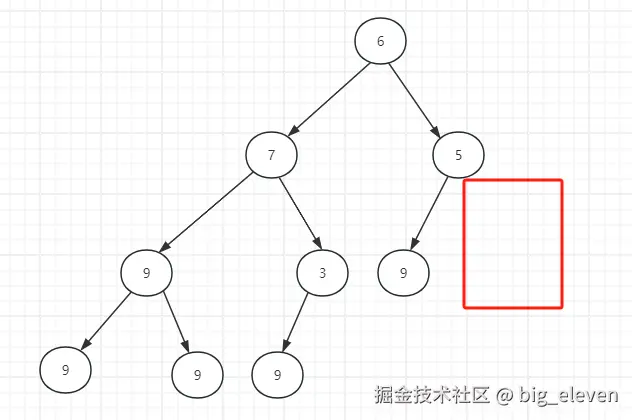
因为倒数第二层,没有达到节点数的最大值
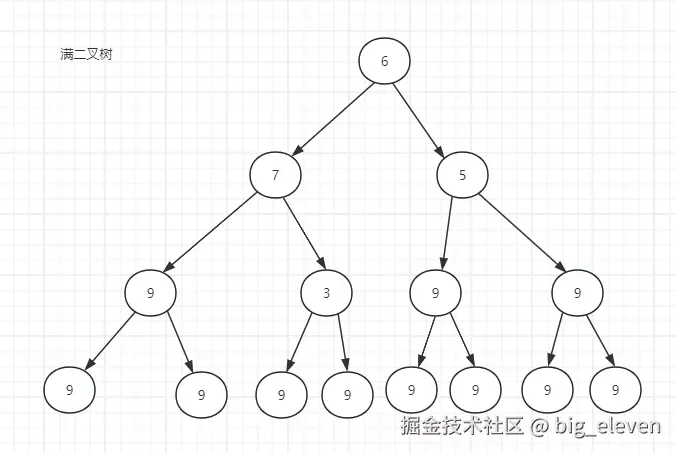
满二叉树
满二叉树是指树的所有层的节点数都达到了最大值