3.6 Linear Discriminants and Selenite Crystals
3.6 线性判别式和透石膏晶体(剪纸 )
3.7 Selenite Crystals bend Space
3.7 透石膏晶体弯曲空间(折叠剪纸 )
3.8 Using transformations to fold
3.8 使用变换 进行折叠
3.9 Transformations change distance and dot products
3.9 变换改变距离和点积
3.10 Kernelized SVMs
3.10 核化SVM
核化SVM
- [折叠和切割定理(the fold and cut theorem)](#折叠和切割定理(the fold and cut theorem))
- 数学表示
-
- [Transformations 变换](#Transformations 变换)
-
- 示例
- [Feature Transformation ↔ Distance Change \text{Feature Transformation} \;\;\leftrightarrow\;\; \text{Distance Change} Feature Transformation↔Distance Change](#Feature Transformation ↔ Distance Change \text{Feature Transformation} ;;\leftrightarrow;; \text{Distance Change} Feature Transformation↔Distance Change)
- 证明
- 核函数
-
- [何构造一个非线性的 SVM?](#何构造一个非线性的 SVM?)
- [有效核(valid kernel)](#有效核(valid kernel))
- [Representer theorem 表示定理](#Representer theorem 表示定理)
- [Kernelized SVM 核化SVM过程推导](#Kernelized SVM 核化SVM过程推导)
- [Kernelized SVM 核化SVM分析](#Kernelized SVM 核化SVM分析)
- [支持向量机 (SVM) 的优点与缺点](#支持向量机 (SVM) 的优点与缺点)
折叠和切割定理(the fold and cut theorem)
基于直觉理解底层数学
折叠和切割定理(the fold and cut theorem),对机器学习很重要。因为判别式(无论是感知器还是支持向量机)的局限性之一是,它们只能使用单次直线切割来划分空间,这意味着我们无法线性求解不可分离分类(linearly non-separable)问题。
我们有别的方式解决,比如KNN最近邻算法。但线性判别式有它们自己的优势,比如简单。
切割示例1




切割示例2



总结
在这个空间中引入折叠,我们就改变了距离的定义。在展开的空间中较远的点,可以变得更近。在空间中较近的点,我们可以拉伸它们之间的空间,可以增加它们的距离。所以折叠无非就是改变距离的定义。
这意味着我能够改变数据点所在的未来空间的距离定义,我将能够计算这两个点之间的距离,使用它来制作非线性分类器(non-linear classifier),我可能能够分离更多的组件或者生成更复杂的决策。在我们讲到那之前,我想给你们一个直观的距离定义,这样我们可以理解距离。我们取两个点,然后计算两点之间的距离,我们有一个公式就是欧几里得距离(euclidean distance)。但是如果我们改变距离定义和函数,那么我们就能够在那个空间中折叠,然后进行切割,我们就能够分离原本不能分离的这两个点。这就是我们想要做的。
数学表示
感知器和SVM对数据非线性可分,起不了作用。所以我们折叠这些空间,就基本上能够从线性分类器转变成分类空间的非线性边界。
有两种数学方式可以实现直觉上的折叠
Transformations 变换
Nonlinear Separation through Transformation
通常用 ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅)来表示,我们可以将示例中的 x x x向量映射到另一个特征空间中,原始特征空间中相距较远的两个点可以在变换(transformed)空间中靠的很近。
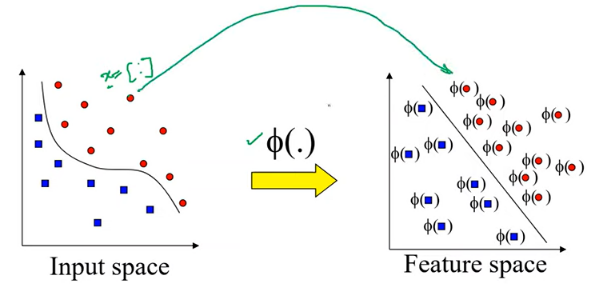
示例
在这些变化中,始终基于特征,不应涉及任何标签
这一点很重要,因为我们要对测试集进行分类,但我们不知道测试集的标签,这也是我们要求的解。要对测试集进行特征变换,然后再代入线性判别式。
对这个线性不可分的数据进行分类
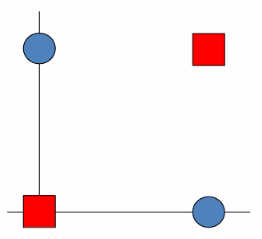
f ( x ; θ ) = w 1 x ( 1 ) + w 2 x ( 2 ) + b = 0 f(x;\theta) = w_{1}x^{(1)} + w_{2}x^{(2)} + b = 0 f(x;θ)=w1x(1)+w2x(2)+b=0
( 0 , 0 ) : b < 0 ( 0 , 1 ) : w 2 + b > 0 ( 1 , 0 ) : w 1 + b > 0 ( 1 , 1 ) : w 1 + w 2 + b < 0 \begin{aligned} (0,0): & \; b < 0 \\ (0,1): & \; w_{2} + b > 0 \\ (1,0): & \; w_{1} + b > 0 \\ (1,1): & \; w_{1} + w_{2} + b < 0 \end{aligned} (0,0):(0,1):(1,0):(1,1):b<0w2+b>0w1+b>0w1+w2+b<0
上述式子相互冲突,解决不了
进行转换:把二维转换成三维,映射到不同的转换空间
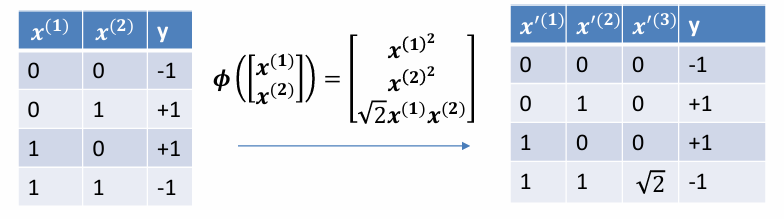
f ( x ; θ ) = w 1 x ( 1 ) + w 2 x ( 2 ) + w 3 x ( 3 ) + b = 0 f(x;\theta) = w_{1}x^{(1)} + w_{2}x^{(2)} + w_{3}x^{(3)} + b = 0 f(x;θ)=w1x(1)+w2x(2)+w3x(3)+b=0
( 0 , 0 , 0 ) : b < 0 ( 0 , 1 , 0 ) : w 2 + b > 0 ( 1 , 0 , 0 ) : w 1 + b > 0 ( 1 , 1 , 2 ) : w 1 + w 2 + 2 w 3 + b < 0 \begin{aligned} (0,0,0): & \; b < 0 \\ (0,1,0): & \; w_{2} + b > 0 \\ (1,0,0): & \; w_{1} + b > 0 \\ (1,1,\sqrt{2}): & \; w_{1} + w_{2} + \sqrt{2}\, w_{3} + b < 0 \end{aligned} (0,0,0):(0,1,0):(1,0,0):(1,1,2 ):b<0w2+b>0w1+b>0w1+w2+2 w3+b<0
由此,我们可以找出符合的数据值(不止一个)
w 1 = 2 , w 2 = 2 , w 3 = − 3 , b = − 1 w_{1} = 2,\quad w_{2} = 2,\quad w_{3} = -3,\quad b = -1 w1=2,w2=2,w3=−3,b=−1
Feature Transformation ↔ Distance Change \text{Feature Transformation} \;\;\leftrightarrow\;\; \text{Distance Change} Feature Transformation↔Distance Change
特征变换改变了两点之间距离或点积的概念
如果我将点积的定义更改为不同的公式,这将改变这些点之间的距离的概念,这相当于进行了一次变换。
欧几里得空间
d ( a , b ) = ∥ a − b ∥ 2 = ( a − b ) T ( a − b ) = a T a + b T b − 2 a T b = k ( a , a ) + k ( b , b ) − 2 k ( a , b ) d(a,b) = \|a - b\|^2 = (a - b)^{T}(a - b) = a^{T}a + b^{T}b - 2a^{T}b\\ =k(a,a) + k(b,b) - 2k(a,b) d(a,b)=∥a−b∥2=(a−b)T(a−b)=aTa+bTb−2aTb=k(a,a)+k(b,b)−2k(a,b)
此时, k ( a , b ) = a T b \color{red}{k(a,b) = a^{T}b} k(a,b)=aTb
特征变换后的空间距离
d ϕ ( a , b ) = ∥ ϕ ( a ) − ϕ ( b ) ∥ 2 d_{\phi}(a,b) = \|\phi(a) - \phi(b)\|^2 dϕ(a,b)=∥ϕ(a)−ϕ(b)∥2
展开
d ϕ ( a , b ) = ( ϕ ( a ) − ϕ ( b ) ) T ( ϕ ( a ) − ϕ ( b ) ) = ϕ ( a ) T ϕ ( a ) + ϕ ( b ) T ϕ ( b ) − 2 ϕ ( a ) T ϕ ( b ) = k ( a , a ) + k ( b , b ) − 2 k ( a , b ) \begin{aligned} d_{\phi}(a,b) &= (\phi(a) - \phi(b))^{T}(\phi(a) - \phi(b)) \\ &= \phi(a)^{T}\phi(a) + \phi(b)^{T}\phi(b) - 2\phi(a)^{T}\phi(b) \\ &= k(a,a) + k(b,b) - 2k(a,b) \end{aligned} dϕ(a,b)=(ϕ(a)−ϕ(b))T(ϕ(a)−ϕ(b))=ϕ(a)Tϕ(a)+ϕ(b)Tϕ(b)−2ϕ(a)Tϕ(b)=k(a,a)+k(b,b)−2k(a,b)
此时,点积/内积公式
k ( a , b ) = ϕ ( a ) T ϕ ( b ) \color{red}{k(a,b) = \phi(a)^{T}\phi(b)} k(a,b)=ϕ(a)Tϕ(b)
距离可以用点积表示,
∥ a ∥ 2 = a T a \|a\|^2 = a^{T}a ∥a∥2=aTa
到目前为止,我们看到变换会改变距离的概念。所以,如果你对一个给定点实施一个变换,对另一个点也实施同样的变换,那么这些点之间的距离就会发生变化。我们知道,距离可以用点积来表示。这意味着,如果我改变点积的定义,首先距离定义会改变,同时意味着会有一个隐式变换,这是改变或者折叠这个特征空间的另一种方式。如果我改变给定特征空间中点积的概念,这自动意味着我已经应用了一个变换。
证明
通过这个例子证明变换如何改变点积的定义。或者为了进行变换的另一种方式是改变点积
2D数据
a = [ a ( 1 ) a ( 2 ) ] , b = [ b ( 1 ) b ( 2 ) ] a = \begin{bmatrix} a^{(1)} \\ a^{(2)} \end{bmatrix}, \quad b = \begin{bmatrix} b^{(1)} \\ b^{(2)} \end{bmatrix} a=[a(1)a(2)],b=[b(1)b(2)]
原本点积公式
a T b = a ( 1 ) b ( 1 ) + a ( 2 ) b ( 2 ) a^{T}b = a^{(1)}b^{(1)} + a^{(2)}b^{(2)} aTb=a(1)b(1)+a(2)b(2)
改变点积公式
k ( a , b ) = ( a T b ) 2 = ( a ( 1 ) b ( 1 ) + a ( 2 ) b ( 2 ) ) 2 \color{red}k(a,b) = (a^{T}b)^{2} = \big(a^{(1)}b^{(1)} + a^{(2)}b^{(2)}\big)^{2} k(a,b)=(aTb)2=(a(1)b(1)+a(2)b(2))2
我们使用变换的话,
ϕ ( u ) = [ u ( 1 ) u ( 2 ) 2 u ( 1 ) u ( 2 ) ] \color{red}{ \phi(u) = \begin{bmatrix} u^{(1)} \\ u^{(2)} \\ \sqrt{2}\,u^{(1)}u^{(2)} \end{bmatrix}} ϕ(u)= u(1)u(2)2 u(1)u(2)
映射后内积,
ϕ ( a ) T ϕ ( b ) = [ a ( 1 ) a ( 2 ) 2 a ( 1 ) a ( 2 ) ] [ b ( 1 ) b ( 2 ) 2 b ( 1 ) b ( 2 ) ] = a ( 1 ) b ( 1 ) + a ( 2 ) b ( 2 ) + 2 a ( 1 ) a ( 2 ) b ( 1 ) b ( 2 ) = ( a ( 1 ) b ( 1 ) + a ( 2 ) b ( 2 ) ) 2 = ( a T b ) 2 = k ( a , b ) \begin{aligned} \color{red}\phi(a)^{T}\phi(b) &= \begin{bmatrix} a^{(1)} & a^{(2)} & \sqrt{2}\,a^{(1)}a^{(2)} \end{bmatrix} \begin{bmatrix} b^{(1)} \\ b^{(2)} \\ \sqrt{2}\,b^{(1)}b^{(2)} \end{bmatrix} \\ &= a^{(1)}b^{(1)} + a^{(2)}b^{(2)} + 2a^{(1)}a^{(2)}b^{(1)}b^{(2)} \\ &= \big(a^{(1)}b^{(1)} + a^{(2)}b^{(2)}\big)^{2} \\ & \color{red}= (a^{T}b)^{2} = \color{red}k(a,b) \end{aligned} ϕ(a)Tϕ(b)=[a(1)a(2)2 a(1)a(2)] b(1)b(2)2 b(1)b(2) =a(1)b(1)+a(2)b(2)+2a(1)a(2)b(1)b(2)=(a(1)b(1)+a(2)b(2))2=(aTb)2=k(a,b)
可以看出,点积和变换是一回事
目的:使用线性判别式或直线切割,来实现线性不可分数据集的线性可分。本质需要进行折叠。
三种方式:改变距离的定义(变换)、改变点积的定义、应用显式变换
折叠空间
改变点积 dot products
改变距离定义
进行特征变换
这4件事情,是完全相同的
ϕ ( x ) = { x 1 2 x 2 2 2 x 1 x 2 } ⟺ a T b ⟶ ( a T b ) 2 \phi(x) = \begin{Bmatrix} x_1^2 \\ x_2^2 \\ \sqrt{2}\,x_1x_2 \end{Bmatrix} \;\;\Longleftrightarrow\;\; a^Tb \;\;\longrightarrow\;\; (a^Tb)^2 ϕ(x)=⎩ ⎨ ⎧x12x222 x1x2⎭ ⎬ ⎫⟺aTb⟶(aTb)2
核函数
何构造一个非线性的 SVM?
- 对数据进行特征变换,然后再应用 SVM
- 选择一个合适的变换(Choosing a transformation)
- 改变点积(内积)的定义,使得隐式的特征变换可以实现非线性分类!
- 选择一个核函数(Choosing a kernel function)
核函数:一个以两个点(两个特征向量)作为输入并生成标量的函数。
Linear K ( x , y ) = x ⋅ y Sigmoid K ( x , y ) = tanh ( a x ⋅ y + b ) Polynomial K ( x , y ) = ( 1 + x ⋅ y ) d KMOD K ( x , y ) = a [ exp ( γ ∥ x − y ∥ 2 + σ 2 ) − 1 ] RBF K ( x , y ) = exp ( − a ∥ x − y ∥ 2 ) Exponential RBF K ( x , y ) = exp ( − a ∥ x − y ∥ ) \begin{array}{ll} \text{Linear} & K(x,y) = x \cdot y \\[6pt] \text{Sigmoid} & K(x,y) = \tanh(ax \cdot y + b) \\[6pt] \text{Polynomial} & K(x,y) = (1 + x \cdot y)^d \\[6pt] \text{KMOD} & K(x,y) = a \left[ \exp\!\left( \frac{\gamma}{\lVert x-y \rVert^2 + \sigma^2} \right) - 1 \right] \\[10pt] \text{RBF} & K(x,y) = \exp\!\left( -a \lVert x-y \rVert^2 \right) \\[6pt] \text{Exponential RBF} & K(x,y) = \exp\!\left( -a \lVert x-y \rVert \right) \end{array} LinearSigmoidPolynomialKMODRBFExponential RBFK(x,y)=x⋅yK(x,y)=tanh(ax⋅y+b)K(x,y)=(1+x⋅y)dK(x,y)=a[exp(∥x−y∥2+σ2γ)−1]K(x,y)=exp(−a∥x−y∥2)K(x,y)=exp(−a∥x−y∥)
K ( x , y ) = x ⋅ y = a T b K(x,y) = x \cdot y=a^Tb K(x,y)=x⋅y=aTb 这个被称为线性核。
K ( x , y ) = ( 1 + x ⋅ y ) d K(x,y) = (1 + x \cdot y)^d K(x,y)=(1+x⋅y)d是多项式核, d d d 可以是任何整数,如果是2,就是二次多项式核。
R B F RBF RBF 是很经典的一种核函数
| 项目 | Value |
|---|---|
| 始终有效的核函数: | ✔ Linear✔ Polynomial✔ RBF✔ Exponential RBF |
| 条件有效的核函数 | ⚠ Sigmoid (参数需限制) |
| 不确定 / 研究型核函数 | ❓ KMOD (不是标准常用核,需单独验证是否半正定) |
有效核(valid kernel)
假设我们有 n n n个训练数据,在所有样本之间应用核函数。假设我们的训练数据中有3个样本,那么我们可以构造一个核矩阵(Kernel matrix),被称为gram 矩阵(gram matrix)。
我们可以计算核值,这通常是一个 n ∗ n n*n n∗n 的方阵。只要这个矩阵是对称的,并且是半正定的。只要这个核矩阵满足这些属性,这就是一个有效核(valid kernel) 这就是核函数成为有效核的额外要求。
Any function k k k can be a kernel if its 'Gram' matrix
K = [ k ( x 1 , x 1 ) k ( x 1 , x 2 ) k ( x 1 , x 3 ) k ( x 2 , x 1 ) k ( x 2 , x 2 ) k ( x 2 , x 3 ) k ( x 3 , x 1 ) k ( x 3 , x 2 ) k ( x 3 , x 3 ) ] K = \begin{bmatrix} k(x_{1}, x_{1}) & k(x_{1}, x_{2}) & k(x_{1}, x_{3}) \\ k(x_{2}, x_{1}) & k(x_{2}, x_{2}) & k(x_{2}, x_{3}) \\ k(x_{3}, x_{1}) & k(x_{3}, x_{2}) & k(x_{3}, x_{3}) \end{bmatrix} K= k(x1,x1)k(x2,x1)k(x3,x1)k(x1,x2)k(x2,x2)k(x3,x2)k(x1,x3)k(x2,x3)k(x3,x3)
is symmetric, positive semi-definite (for all given data). 对称的,并且是半正定
什么叫半正定?
K K K 是上面的核矩阵
n n n 是矩阵的size,也就是训练数据个数
取任意系数向量 c = [ c 1 , c 2 . . . c n ] T c = [c_1, c_2... c_n]^T c=[c1,c2...cn]T,有:
c T K c ≥ 0 c^T K c \geq 0 cTKc≥0
这个结果在数学上证明始终 ≥ 0 \geq 0 ≥0 就是半正定。如果是 > > >就是正定。
Representer theorem 表示定理
权重向量 w w w 可以用原始示例的未来值的权重表示。
在SVM线性核中,我们寻找 w w w。现在我们不是寻找 w w w ,而是选择寻找 α \alpha α,我们实际就拥有一个权重向量,可以进行分类。
We know that the discriminant function of the SVM can be written as: 我们知道SVM的判别函数可以写成:
f ( x ) = w T x + b f(x) = \mathbf{w}^T x + b f(x)=wTx+b
The Representer theorem \textbf{Representer theorem} Representer theorem (Scholkopf 2001) allows us to represent the SVM weight vector as a linear combination of input vectors with each example's contribution weighted by a factor α i \alpha_i αi:
表示定理 \textbf{ 表示定理 } 表示定理 (Scholkopf 2001) 允许我们将 SVM 权重向量表示为输入向量的线性组合,其中每个示例的贡献都由因子 α i \alpha_i αi 加权:
w = ∑ i = 1 N α i x i \mathbf{w} = \sum_{i=1}^{N} \alpha_i x_i w=i=1∑Nαixi
举例
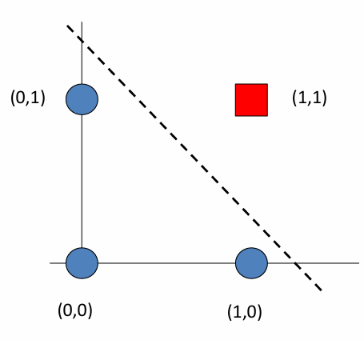
w ⃗ = α 1 [ 0 0 ] + α 2 [ 1 0 ] + α 3 [ 1 1 ] + α 4 [ 0 1 ] \vec{w} = \alpha_1 \begin{bmatrix} 0\\ 0 \end{bmatrix}+ \alpha_2 \begin{bmatrix} 1 \\ 0 \end{bmatrix}+ \alpha_3 \begin{bmatrix} 1 \\ 1 \end{bmatrix}+ \alpha_4 \begin{bmatrix} 0 \\ 1 \end{bmatrix} w =α1[00]+α2[10]+α3[11]+α4[01]
理解这个定理非常重要,因为它有助于理解机器学习。
我们接下来要做的事情。简而言之,如果您有一堆示例,那么支持向量机的权重向量可以表示为这些示例权重 α \alpha α 的线性组合,因为我们不知道支持向量机的最佳权重向量是多少。
我们通过优化找到答案。
我们可以通过直接搜索 w w w 来实现,这是我们之前一直在做的事情,或者我们可以使用一个优化程序来找到这些给定示例的 α \alpha α 值,这也是等效的。
示例权重 α 的线性组合优化 ⟺ 直接搜索 w \color{red}{ 示例权重 \alpha 的线性组合优化 \;\;\Longleftrightarrow\;\; 直接搜索 w} 示例权重α的线性组合优化⟺直接搜索w
Kernelized SVM 核化SVM过程推导
这里是核化SVM的推导过程:
根据表示定理
w = ∑ i = 1 N α i x i \mathbf{w} = \sum_{i=1}^{N} \alpha_i x_i w=i=1∑Nαixi
代入原本的线性SVM公式,
f ( x ) = w T x + b = b + ∑ j = 1 N α j x j T x f(x) = \mathbf{w}^T x + b = b + \sum_{j=1}^{N} \alpha_j x_j^T x f(x)=wTx+b=b+j=1∑NαjxjTx
注意,这里测试样本与每个输入样本之间存在一个点积。 点积记作,
k ( u , v ) = u T v k(u,v) = u^T v k(u,v)=uTv
代入线性SVM 的 f ( x ) f(x) f(x)公式,
f ( x ) = b + w T x = b + ∑ j = 1 N α j k ( x j , x ) k ( x j , x ) 称为 K e r n e l T r i c k 或者说核化 f(x) = b + \mathbf{w}^T x = b + \sum_{j=1}^{N} \alpha_j k(x_j, x) \quad\quad k(x_j, x)称为Kernel\ Trick\ 或者说核化 f(x)=b+wTx=b+j=1∑Nαjk(xj,x)k(xj,x)称为Kernel Trick 或者说核化
接下来,
w T w = ( ∑ i = 1 N α i x i ) T ( ∑ j = 1 N α j x j ) = ∑ i = 1 N ∑ j = 1 N α i α j k ( x i , x j ) \mathbf{w}^T \mathbf{w} = \left( \sum_{i=1}^{N} \alpha_i x_i \right)^T \left( \sum_{j=1}^{N} \alpha_j x_j \right) = \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j k(x_i, x_j) wTw=(i=1∑Nαixi)T(j=1∑Nαjxj)=i=1∑Nj=1∑Nαiαjk(xi,xj)
由此,代入SVM变成,

推导完成。
这两个支持向量机公式本质是一样的,右侧公式好处是经过核函数核化,比原来的公式更有通用性。只要修改内积公式,就可以支持非线性可分。在左边,需要对 X X X 进行显式变换(transmition)才能实现非线性可分。这是实体化(carnalized)和非实体化支持向量机之间的主要区别。
Kernelized SVM 核化SVM分析
这是核化SVM的优化函数,也是优化问题。
min α , b ∑ i = 1 N ∑ j = 1 N α i α j k ( x i , x j ) + C N ∑ i = 1 N max { 0 , 1 − y i ( b + ∑ j = 1 N α j k ( x i , x j ) ) } \min_{\alpha, b} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j \, k(x_i, x_j) \; + \; \frac{C}{N} \sum_{i=1}^{N} \max \left\{ 0, \; 1 - y_i \left( b + \sum_{j=1}^{N} \alpha_j \, k(x_i, x_j) \right) \right\} α,bmini=1∑Nj=1∑Nαiαjk(xi,xj)+NCi=1∑Nmax{0,1−yi(b+j=1∑Nαjk(xi,xj))}
现在我们要解决的不是最小化 w w w,而是最小化 α \alpha α 和 b b b。如果我们解决了这个优化问题,就得到了给定SVM决策函数。
f ( x ) = b + ∑ j = 1 N α j k ( x j , x ) f(x) = b + \sum_{j=1}^{N} \alpha_j \, k(x_j, x) f(x)=b+j=1∑Nαjk(xj,x)
只要代入给定的测试集数据,就能得到出它们对应的标签。
支持向量机 (SVM) 的优点与缺点
优点 (Strengths)
- 只需少量训练点就能确定最终的分类边界 ------支持向量 (Support Vectors)
- 最大化间隔,并且可以 核化 (kernelized)
- 训练相对容易 ------不会陷入局部最优,不像神经网络
- 在高维数据上表现良好,可扩展性较好
- 分类器复杂度与误差之间的权衡可以通过参数 C 显式控制
- 可以处理非传统数据,例如字符串和树结构,而不仅仅是特征向量
缺点 (Weaknesses)
- 需要选择一个"合适的"核函数