我爱学算法之—— BFS之最短路径问题

一、迷宫中离入口最近的出口

题目解析

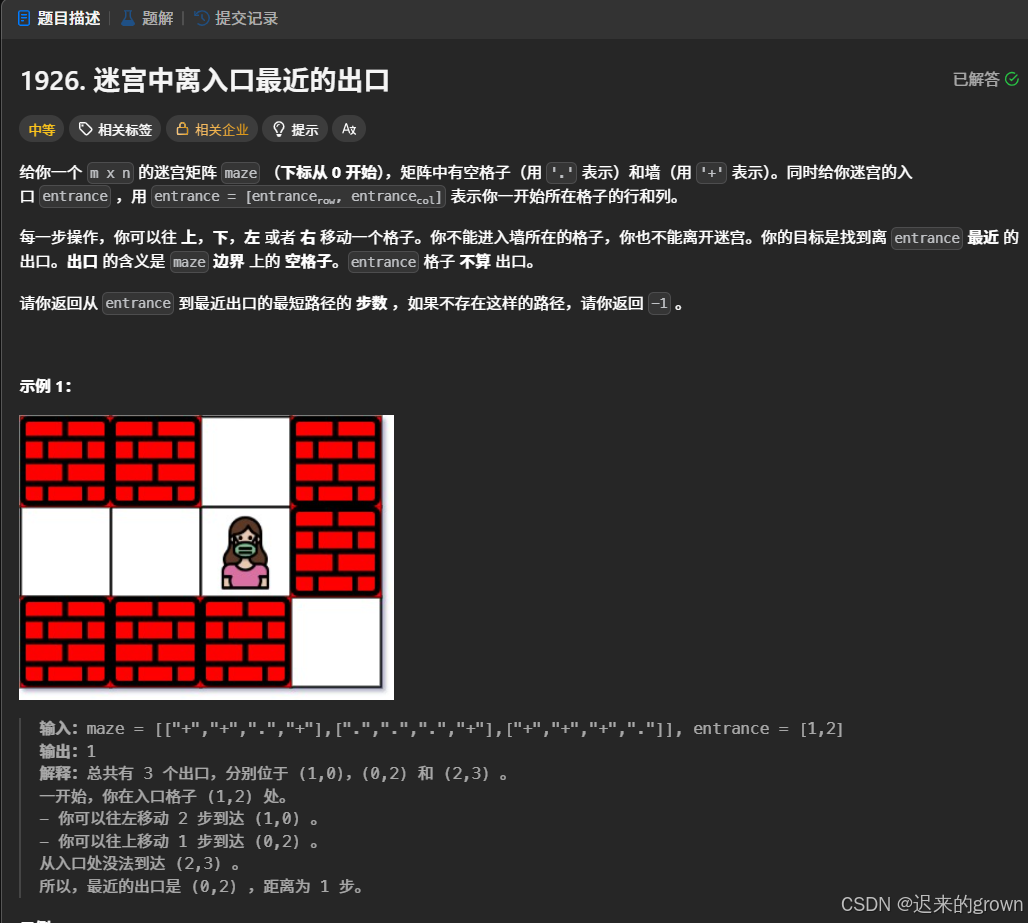
给定一个n*m的迷宫矩阵，其中.表示空格子，+表示障碍物；

还给了迷宫的起始位置，要我们求从该位置开始，走出迷宫需要的最低步数

算法思路

这道题，我们只需从给定的起始位置开始，进行一次BFS遍历，并且记录到每一个位置的距离（-1表示到达不了该位置）

初始化

• 方向数组控制上下左右移动，vis 数组标记已访问节点，length 数组记录到入口的步数（初始 - 1）。
• 入口入队，标记访问，步数设为 0。

BFS 遍历

• 出队队首节点，遍历 4 个相邻方向，筛选合法（边界内、可通行、未访问）节点。
• 合法节点标记访问、记录步数（前节点 + 1），入队继续遍历。

找最短出口

• 遍历迷宫边界的可通行节点，筛选出 length 非 - 1 的节点，取最小步数。
• 无符合条件节点则返回 - 1，否则返回最小步数

代码实现

class Solution {
public:
    typedef pair<int, int> PII;
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
    bool vis[101][101];
    int length[101][101]; // 步数
    int nearestExit(vector<vector<char>>& maze, vector<int>& entrance) {
        memset(&length, -1, sizeof(length));
        int n = maze.size();
        int m = maze[0].size();
        int x = entrance[0];
        int y = entrance[1];
        bfs(maze, x, y);
        length[x][y] = INT_MAX;
        int ret = INT_MAX;
        // 在边缘找结果
        for (int i = 0; i < n; i++) {
            if (maze[i][0] == '.' && length[i][0] != -1)
                ret = min(ret, length[i][0]);
            if (maze[i][m - 1] == '.' && length[i][m - 1] != -1)
                ret = min(ret, length[i][m - 1]);
        }
        for (int j = 0; j < m; j++) {
            if (maze[0][j] == '.' && length[0][j] != -1)
                ret = min(ret, length[0][j]);
            if (maze[n - 1][j] == '.' && length[n - 1][j] != -1)
                ret = min(ret, length[n - 1][j]);
        }
        if (ret == INT_MAX)
            return -1;
        return ret;
    }
    void bfs(vector<vector<char>>& maze, int i, int j) {
        int n = maze.size();
        int m = maze[0].size();
        length[i][j] = 0;
        vis[i][j] = true;
        queue<PII> q;
        q.push({i, j});
        while (q.size() > 0) {
            auto [a, b] = q.front();
            q.pop();
            for (int k = 0; k < 4; k++) {
                int x = a + dx[k];
                int y = b + dy[k];
                if (x >= 0 && x < n && y >= 0 && y < m && maze[x][y] == '.' &&
                    vis[x][y] == false) {
                    vis[x][y] = true;
                    length[x][y] = length[a][b] + 1;
                    q.push({x, y});
                }
            }
        }
    }
};

二、最小基因变化

题目解析

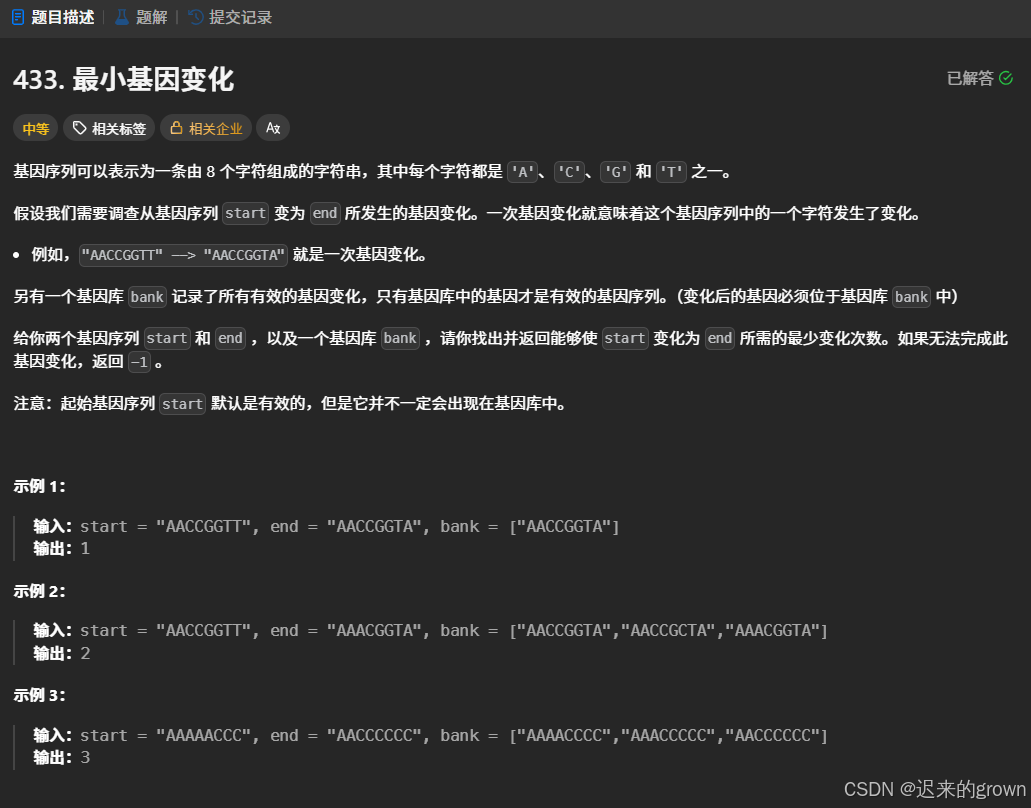
这道题，给定起始字符串和结果字符串，和基因库bank。

要我们求start通过几次基因变化能够变成end。（基因变化：基因序列中的一个字符发生了变化）

在基因变化的过程中，中间变化的序列必须在基因库bank中。

算法思路

初看这道题，感觉这跟BFS有什么关系啊？诶，还真有关系

在BFS遍历的过程中，之前都是判断某一个位置的相邻位置是否满足条件；而这里，应该字符串的相邻字符串就是变化一个字符产生的字符串。

那在进行BFS遍历时，遍历到一个字符串，我们之前枚举（遍历）出所有的相邻字符串，然后判断它是否满足条件（是否在基因库bank中）满足条件就放入队列。

去重 ： 在进行BFS的过程中，遍历所有相邻字符串，肯定会存在重复的字符串；所有只有字符串在基因库bank中并且没有遍历过，才满足条件，才能放入队列中。

注意：

题目要求我们求基因变化的最小次数，只需在BFS的过程中统计一下步数即可。

此外，end序列可能不在基因库bank中的；如果end不在bank中，那就不用进行BFS了，直接返回-1即可。

代码实现

class Solution {
public:
    char str[4] = {'A', 'C', 'G', 'T'};
    int minMutation(string startGene, string endGene, vector<string>& bank) {
        int ret = 0;
        unordered_set<string> hash(bank.begin(), bank.end());
        unordered_set<string> vis;
        if (startGene == endGene)
            return 0;
        if (hash.count(endGene) == 0)
            return -1;
        queue<string> q;
        q.push(startGene);
        vis.insert(startGene);
        while (q.size() > 0) {
            ret++;
            int n = q.size();
            while (n--) {
                string s = q.front();
                q.pop();
                for (int i = 0; i < s.size(); i++) {
                    for (int j = 0; j < 4; j++) {
                        if (s[i] == str[j])
                            continue;
                        string tmp = s;
                        tmp[i] = str[j];
                        if (hash.count(tmp) > 0 && vis.count(tmp) == 0) {
                            q.push(tmp);
                            vis.insert(tmp);
                            if (tmp == endGene)
                                return ret;
                        }
                    }
                }
            }
        }
        return -1;
    }
};

三、单词接龙

题目解析

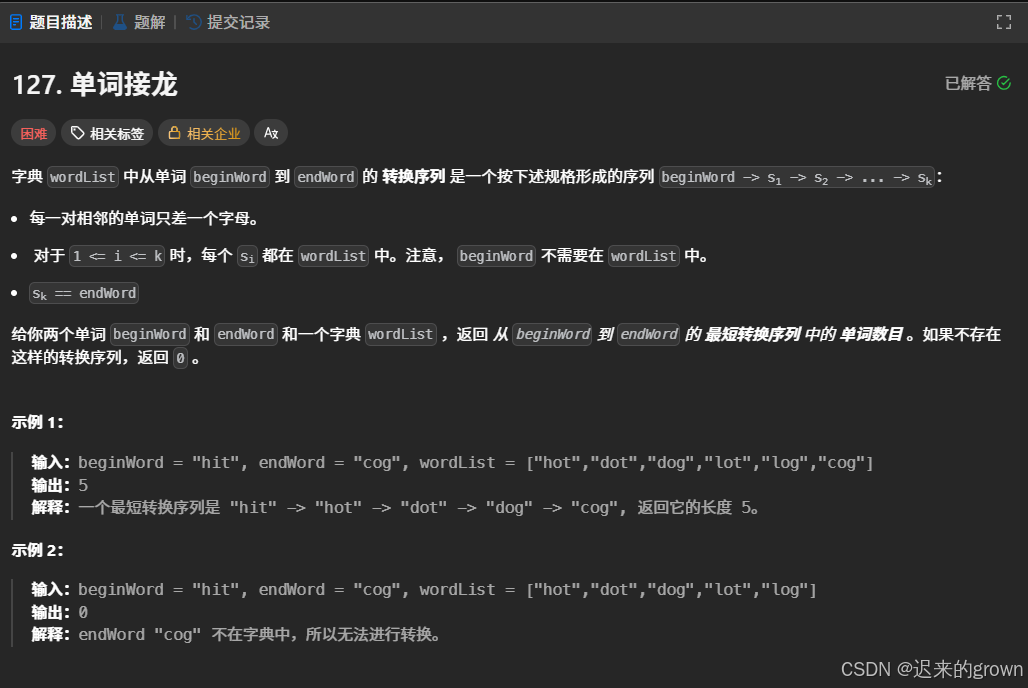
这道题和基因变化类似，也是给定一个beginWord起始字符串和一个endWord终止字符串，以及单词字典worldList。

每次字符串可以变化一个字符，要求beginWord变化成endWord的最短转换序列的长度

算法思路

这道题的整体思路和基因变化一样，也是从beginWord进行BFS遍历

• 每个单词是一个「节点」，两个单词若仅 1 个字符不同且在词库中，则为「相邻节点」（可直接转换）。
• 找从 beginWord 到 endWord 的「最短相邻转换次数 + 1」。

前置判断：

• 若 endWord 不在词库 wordList 中，直接返回 0（无法到达）。

BFS：

• 初始化：词库转哈希集（快速查询），访问集记录已遍历单词（去重），起始单词入队并标记访问，长度初始为 1。
• 层级遍历：
  • 每轮遍历当前队列中所有单词（同一转换步数的单词），长度+ 1（进入下一轮转换）。
  • 对每个单词，遍历其每个字符位，尝试替换为 a-z 中所有字符（跳过原字符，避免无效替换）。
  • 若替换后得到 endWord，直接返回当前步数；若替换后单词在词库且未访问，标记访问并入队。

结果 ：队列遍历完仍未找到 endWord，返回 0（无有效转换路径）。

代码实现

class Solution {
public:
    int ladderLength(string beginWord, string endWord,
                     vector<string>& wordList) {
        unordered_set<string> hash(wordList.begin(), wordList.end());
        unordered_set<string> vis;
        string change;
        queue<string> q;
        if (hash.count(endWord) == 0)
            return 0;
        q.push(beginWord);
        vis.insert(beginWord);
        int ret = 1;
        while (q.size() > 0) {
            int n = q.size();
            ret++;
            while (n--) {
                string s = q.front();
                q.pop();
                for (int i = 0; i < s.size(); i++) {
                    for (char ch = 'a'; ch <= 'z'; ch++) {
                        string tmp = s;
                        tmp[i] = ch;
                        if (tmp == endWord)
                            return ret;
                        if (hash.count(tmp) > 0 && vis.count(tmp) == 0) {
                            q.push(tmp);
                            vis.insert(tmp);
                        }
                    }
                }
            }
        }
        return 0;
    }
};

四、为高尔夫比赛砍树

题目解析

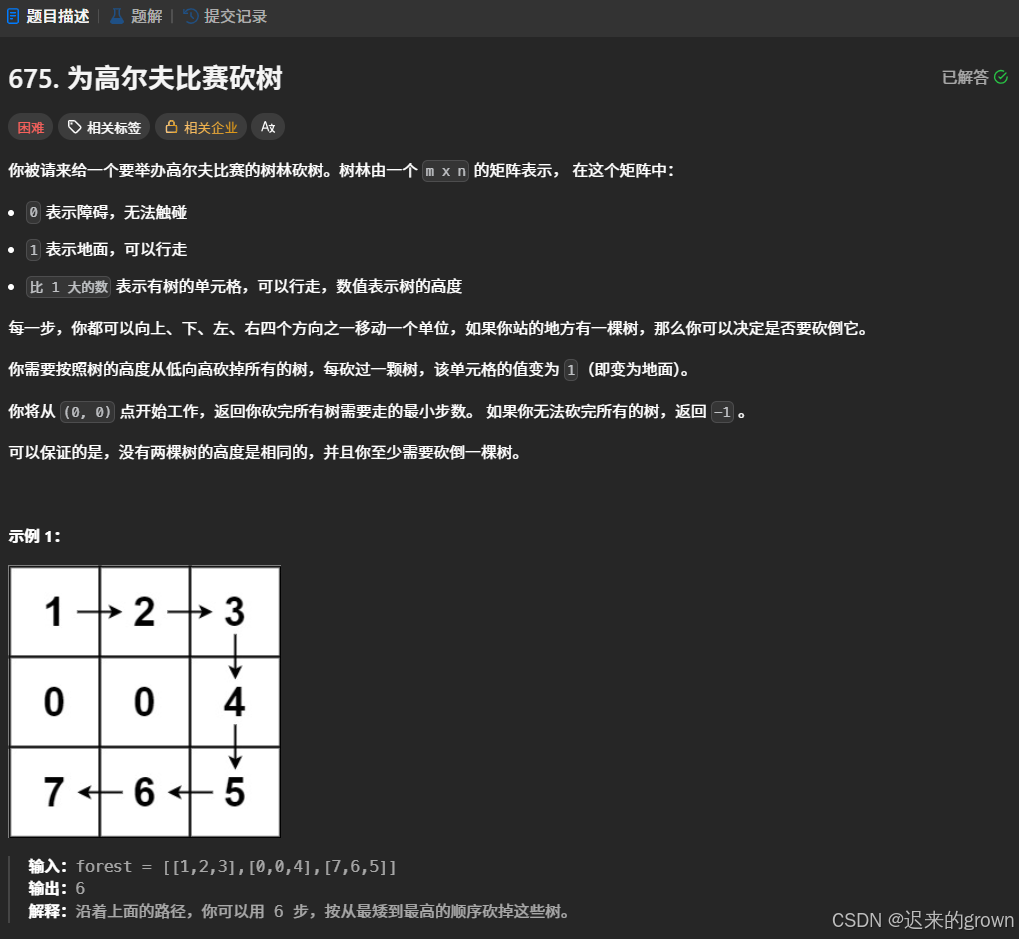
给定一个n*m的二维数组，其中0表示障碍，1表示地面，>1表示有树的单元格。其中0障碍不能行走。

现在要从(0,0)位置开始工作，可以向上、下、左、右移动一个单位，如果当前位置有一棵树，可以砍掉也可以不砍掉。

题目要求：我们必须按照树的高度，从低到高砍掉所有的树。

算法思路

虽然这道题是困难级别，但其实是非常简单的。

我们要从低到高的砍掉所有的树，那肯定要知道：按照树高度从低到高排序后，砍树的顺序吧。

1. 获取砍树顺序：

遍历forest，按照树的高度从低到高，将树的下标存储起来。

2. BFS求最短路径：

有了砍树的顺序，也知道起始位置和目标位置，进行BFS遍历，求出最短路径。

3. 统计结果

创建ret变量，记录BFS求出的最短路径的和，最后返回即可。

代码实现

class Solution {
public:
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
    typedef pair<int, int> PII;
    int bfs(vector<vector<int>>& forest, int src_x, int src_y, int des_x,
            int des_y) {
        if (src_x == des_x && src_y == des_y)
            return 0;
        int n = forest.size();
        int m = forest[0].size();
        vector<vector<bool>> vis(n, vector<bool>(m, false));
        queue<PII> q;
        q.push({src_x, src_y});
        vis[src_x][src_y] = true;
        int ret = 0;
        while (q.size() > 0) {
            ret++;
            int sz = q.size();
            while (sz--) {
                auto [a, b] = q.front();
                q.pop();
                for (int i = 0; i < 4; i++) {
                    int x = a + dx[i];
                    int y = b + dy[i];
                    if (x == des_x && y == des_y)
                        return ret;
                    if (x >= 0 && x < n && y >= 0 && y < m &&
                        vis[x][y] == false && forest[x][y] != 0) {
                        vis[x][y] = true;
                        q.push({x, y});
                    }
                }
            }
        }
        return -1;
    }
    int cutOffTree(vector<vector<int>>& forest) {
        map<int, PII> hash;
        int n = forest.size();
        int m = forest[0].size();
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (forest[i][j] > 1)
                    hash.insert({forest[i][j], {i, j}});
            }
        }
        int ret = 0;
        int src_x = 0, src_y = 0;
        for (auto& e : hash) {
            int des_x = e.second.first;
            int des_y = e.second.second;
            int tmp = bfs(forest, src_x, src_y, des_x, des_y);
            if (tmp == -1)
                return -1;
            ret += tmp;
            src_x = des_x;
            src_y = des_y;
        }
        return ret;
    }
};

本篇文章到这里就结束了，感谢支持

我的博客即将同步至腾讯云开发者社区，邀请大家一同入驻：https://cloud.tencent.com/developer/support-plan?invite_code=2oul0hvapjsws