LeetCode 0085.最大矩形：单调栈

【LetMeFly】85.最大矩形：单调栈

力扣题目链接：https://leetcode.cn/problems/maximal-rectangle/

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：

复制代码

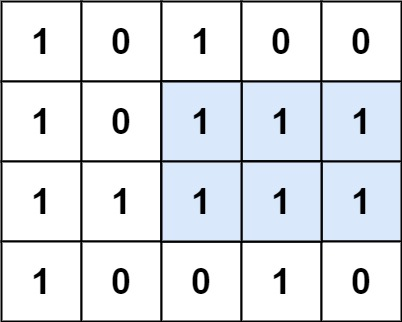
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：6
解释：最大矩形如上图所示。

示例 2：

复制代码

输入：matrix = [["0"]]
输出：0

示例 3：

复制代码

输入：matrix = [["1"]]
输出：1

提示：

rows == matrix.length
cols == matrix[0].length
1 <= row, cols <= 200
matrix[i][j] 为 '0' 或 '1'

解题方法：单调栈

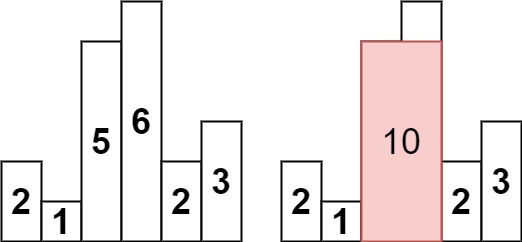
先看84. 柱状图中最大的矩形，求n个相邻柱子的最大面积：

使用一个单调递增栈，柱子前后加两个高度为0的哨兵。

某个柱子被逐出栈时，说明其左右最多能延伸到的柱子分别是"栈顶柱子"、"将其逐出的柱子"（左右不含），以其为高的最大矩形面积为其高 × ( 右柱子 − 左柱子 − 1 ) 其高\times(右柱子-左柱子-1) 其高×(右柱子−左柱子−1)。
cpp 复制代码
/*
 * @LastEditTime: 2026-01-11 22:44:08
 */
class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        stack<int> idx;
        heights.insert(heights.begin(), 0);
        heights.push_back(0);
        int ans = 0;
        for (int i = 0; i < heights.size(); i++) {
            while (idx.size() && heights[i] < heights[idx.top()]) {
                int lastIdx = idx.top();
                idx.pop();
                ans = max(ans, heights[lastIdx] * (i - idx.top() - 1));
            }
            idx.push(i);
        }
        return ans;
    }
};

这道题是一样的，对于 n n n行的matrix，以第 i i i行为底第 1 1 1行为顶的子矩阵共 n n n个，可以做 n n n次上面的单调栈。

对于下面的matrix：

复制代码

1 0 1 0 0
1 0 1 1 1
1 1 1 1 1

相当于：

第 1 1 1行到第 1 1 1行的子矩阵：
复制代码
```
1 0 1 0 0
```
相当于高为1 0 1 0 0的柱子，做一次单调栈；
第 1 1 1行到第 2 2 2行的子矩阵：
复制代码
```
1 0 1 0 0
1 0 1 1 1
```
相当于高为2 0 2 1 1的柱子，做一次单调栈；
第 1 1 1行到第 3 3 3行的子矩阵：
复制代码
```
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
```
相当于高为3 0 3 2 2的柱子，做一次单调栈。

其中由第 i i i行为底过度到由第 i + 1 i+1 i+1行为底时，可以借助上一行为底时的柱子高度快速更新新柱子的高度。

时间复杂度 O ( s i z e ( m a t r i x ) ) O(size(matrix)) O(size(matrix))
空间复杂度 O ( s i z e ( m a t r i x [ 0 ] ) ) O(size(matrix[0])) O(size(matrix[0]))，需要一行的空间

AC代码

C++

cpp 复制代码

/*
 * @LastEditTime: 2026-01-11 23:13:41
 */
class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        int ans = 0;
        vector<int> heights(matrix[0].size() + 2);
        for (int i = 0; i < matrix.size(); i++) {
            matrix[i].insert(matrix[i].begin(), '0');
            matrix[i].push_back('0');
            stack<int> st;
            for (int j = 0; j < matrix[i].size(); j++) {
                heights[j] = heights[j] && matrix[i][j] == '1' ? heights[j] + 1 : matrix[i][j] == '1';
                while (st.size() && heights[j] < heights[st.top()]) {  // 记得st.size()也要判断，否则哨兵0会驱逐哨兵0
                    int idx = st.top();
                    st.pop();
                    ans = max(ans, heights[idx] * (j - st.top() - 1));
                }
                st.push(j);
            }
        }
        return ans;
    }
};

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

千篇源码题解已开源