2025杭电多校第十场 Cut Check Bit、Multiple and Factor 个人题解

Multiple and Factor

根号分治 #数学

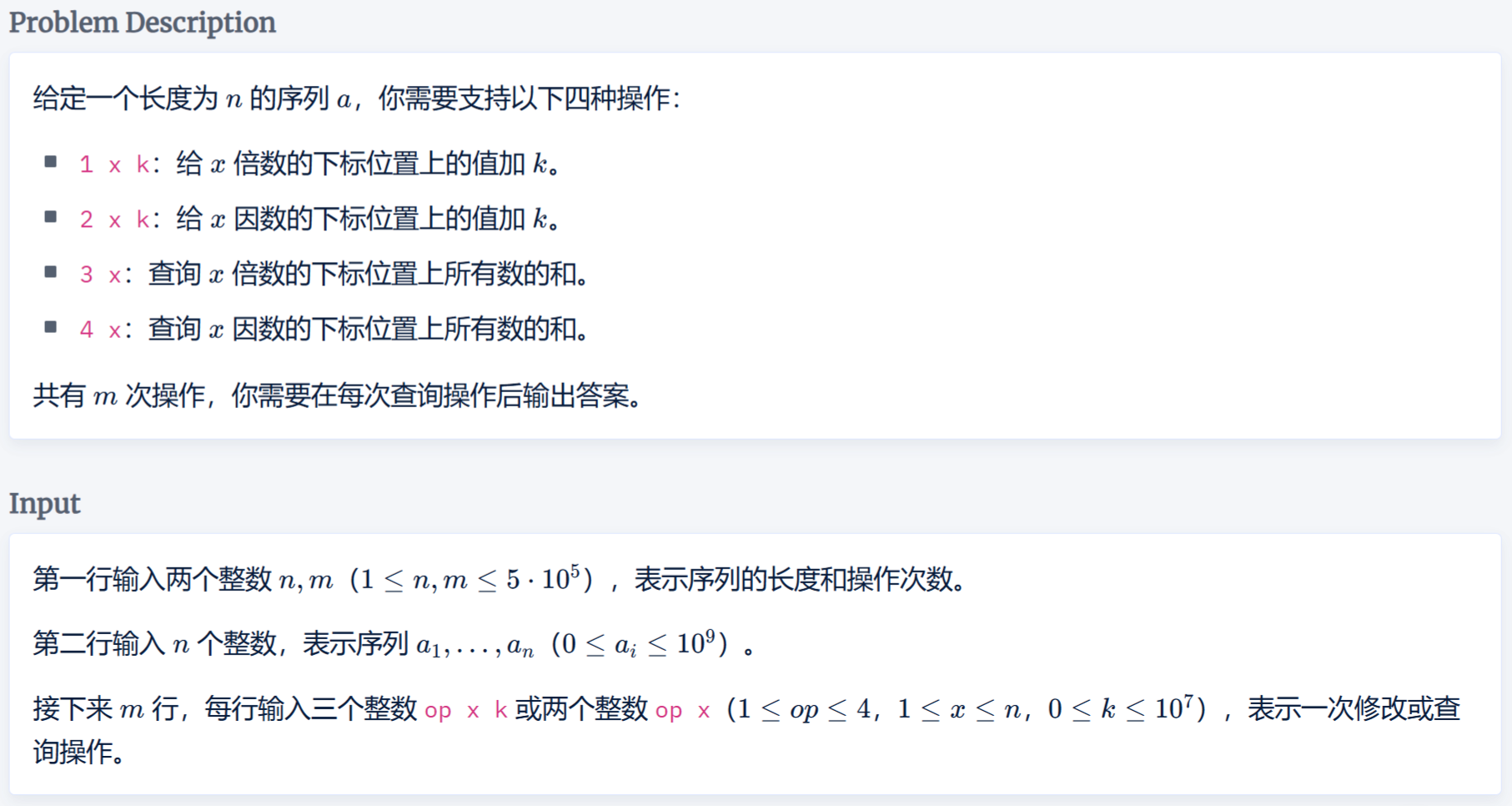
题目

思路

本题采用根号分治 的思想，令\(B=\sqrt{ n }\)，将下标分为\(1\leq i\leq B\)与\(B<i\leq n\)两类数进行维护

数组\(a[N]\)用于储存初始权值

操作一：令\(x\)的所有倍数位置\(+k\)

• 若\(x\leq B\)：
  • 创建数组\(add[B]\)，作为小数倍数和的加法懒标记
  • 直接 \(add[x]+=k\)即可
  • 时间复杂度\(o(1)\)
• 若\(x>B\)：
  • 可知此时的\(x\)的倍数个数不会超过\(B\)个，因此可以暴力解决
  • 枚举\(x\)的所有倍数\(tx\)，\(a[tx]+=k\)
  • 时间复杂度\(o(B)\)

操作二：令\(x\)的所有因数位置\(+k\)

• 直接枚举\(x\)的所有因数\(d\)
• \(a[d]+=k\ [\ d\ |\ x\ ]\)
• 时间复杂度\(o(\sqrt{ n })\)

操作三：查询\(x\)的所有倍数位置的权值和

• 若\(x>B\)：
  • 先暴力枚举\(x\)的所有倍数\(tx\)，\(ans+=a[tx]\)
  • 接下来需要处理\(1\leq i\leq B\)部分的加法懒标记：
    • 设集合\(S_{i}=\{ j\ |\ j=t\times i\ ,\ j\leq n\ ,\ t\geq 1 \}\)，表示所有小于\(n\)的\(i\)的倍数集合
    • 可知\(S_{i}\cap S_{x}=S_{lcm(x,i)}\)
    • \(add[i]\)对答案的贡献即\(add[i]\times S_{lcm(x,i)}.size\)
    • 而\(S_{j}.size=\left\lfloor \frac{n}{j} \right\rfloor\)
    • 因此\(ans+=add[i]\times \left\lfloor \frac{n}{lcm(x,i)} \right\rfloor\)
  • 时间复杂度\(o(B+B\log n)\)，\(\log n\)来自\(lcm(x,i)\)
• 若\(x\leq B\)：
  • 这些数不好用懒标记维护，所以直接每次修改都暴力维护
  • 创建数组\(addmul[B]\)，用于直接储存操作三小数询问的答案
  • 进行操作一时：(令\(x\)的所有倍数位置\(+k\))
    • 考虑直接更新\(1\leq i\leq B\)的\(addmul[i]\)
    • 同样考虑\(S_{i}\)与\(S_{x}\)两个集合，可得\(addmul[i]+=k\times\left\lfloor \frac{n}{lcm(x,i)} \right\rfloor\)
    • 时间复杂度\(o(B\log n)\)
  • 进行操作二时：(令\(x\)的所有因数位置\(+k\))
    • 考虑直接更新\(1\leq i\leq B\)的\(addmul[i]\)
    • 首先\(i\)必须是\(x\)的因数才会被更新到，即\(i\ |\ x\)
    • 设\(t\times i=x\)，若\(d\ |\ t\)，则\((d\times i)\ |\ x\)，因此\(d\)的数量即为又是\(i\)的倍数又是\(x\)的因数的个数
    • 创建数组\(d[B]\)，\(d[i]\)表示数字\(i\)的因数个数，求\(d\ |\ t\)的个数即\(d[t]=d\left[ \frac{x}{i} \right]\)
    • 因此\(addmul[i]+=k\times d\left[ \frac{x}{i} \right]\)
    • 时间复杂度\(o(B)\)

操作四：查询\(x\)的所有因数位置的权值和

• 先暴力枚举\(x\)的所有因数\(d\)，\(ans+=a[d]\)
• 接下来处理小数部分的加法懒标记：
  • 对于\(1\leq i\leq B\)且\(i\ |\ x\)，同样也是考虑"又是\(i\)的倍数又是\(x\)的因数的个数"
  • 因此\(ans+=d\left[ \frac{x}{i} \right]\times add[i]\)
• 时间复杂度\(o(\sqrt{ n }+B)\)

对于数组\(d[B]\)，可以通过类似欧拉筛的方法预处理：

• 枚举\(1\leq i\leq n\)，对于每个\(i\)再枚举\(k\times i\leq n\)，\(d[k\times i]++\)
• 对于每个确定的\(i\)，将会枚举\(\left\lfloor \frac{n}{i} \right\rfloor\)个\(k\)，因此总枚举次数为\(\sum_{i=1}^n\left\lfloor \frac{n}{i} \right\rfloor\)
• 复杂度为\(o\left( \sum_{i=1}^n\left\lfloor \frac{n}{i} \right\rfloor \right)=o\left( \sum_{i=1}^n \frac{n}{i} \right)=o\left( n·\sum_{i=1}^n \frac{1}{i} \right)\)，由\(\sum_{n=1}^x \frac{1}{n}\leq 1+\ln x\)可知，复杂度为\(o(n\log n)\)（文末证明）

至此，由于\(B=\sqrt{ n }\)，总复杂度来到\(o(n\log n+m·\sqrt{ n }·\log n)\)，但由于\(\sqrt{ n }·\log n\)的原因，会\(TLE\)

因此考虑预处理\(gcd(a,b)\)从而将\(\log n\)消去：

• 因为调用时\(lcm(x,i)\)中\(1\leq i\leq B\)，而对于\(x>B\)，辗转相除一次之后也将变为\(x\leq B\) ，因此仅预处理所有\(1\leq a,b\leq B\)的\(gcd(a,b)\)
• 枚举所有\(1\leq i<j\leq B\)，复杂度为\(o(B^2)=o(n)\)

预处理后复杂度为\(n\log n+m·\sqrt{ n }\) 可以通过！

代码实现

#include<iostream>
#include<vector>
#include<cmath>
#include<queue>
#include<algorithm>
#include<set>
#include<stack>
#include<unordered_map>
using namespace std;
using ll = long long;
#define int ll
#define rep(i, a, b) for(int i = (a); i <= (b); i ++)
#define per(i, a, b) for(int i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';

const int N = 5e5 + 5, M = 710;
int n, m, a[N], gcd[M][M], B, add[M], d[N], ansmul[M];

constexpr void init() {
    rep(i, 1, B) {
        rep(j, i + 1, B) {
            gcd[i][j] = __gcd(i, j);
        }
    }
    rep(i, 1, n) {
        for (int j = i;j <= n;j += i)d[j]++;
    }
}

constexpr int g(int x, int y) {
    if (x == y)return x;
    if (x > y)swap(x, y);
    if (x <= M - 1 && y <= M - 1 && gcd[x][y])return gcd[x][y];
    return __gcd(x, y);
}

constexpr int lcm(int x, int y) {
    return x * y / g(x, y);
}

void eachT() {
    cin >> n >> m;
    B = sqrt(n);
    init();
    rep(i, 1, n) cin >> a[i];
    rep(i, 1, B) {
        for (int j = i;j <= n;j += i)ansmul[i] += a[j];
    }
    while (m--) {
        int op;cin >> op;
        if (op == 1) {
            int x, k;cin >> x >> k;
            if (x <= B)add[x] += k;
            else {
                for (int i = x;i <= n;i += x) a[i] += k;
            }
            rep(i, 1, B)ansmul[i] += n / lcm(x, i) * k;
        } else if (op == 2) {
            int x, k;cin >> x >> k;
            for (int i = 1;i * i <= x;i++) {
                if (x % i != 0)continue;
                a[i] += k;
                if (i * i != x)a[x / i] += k;
            }
            rep(i, 1, B)if (x % i == 0)ansmul[i] += d[x / i] * k;
        } else if (op == 3) {
            int x;cin >> x;
            int ans = 0;
            if (x <= B) {
                ans = ansmul[x];
            } else {
                for (int i = 1;i * x <= n;i++)ans += a[i * x];
                rep(i, 1, B)ans += n / lcm(x, i) * add[i];
            }
            cout << ans << '\n';
        } else {
            int x;cin >> x;
            int ans = 0;
            for (int i = 1;i * i <= x;i++) {
                if (x % i != 0)continue;
                ans += a[i];
                if (i * i != x)ans += a[x / i];
            }
            rep(i, 1, B) {
                if (x % i != 0)continue;
                ans += add[i] * d[x / i];
            }
            cout << ans << '\n';
        }
    }
}

signed main() {
    // cout << sqrt(5e5) << '\n';
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    ll t = 1;
    //cin >> t;
    while (t--) {
        eachT();
    }
}

关于调和级数复杂度的证明

\[\sum_{n=1}^x \frac{1}{n}\leq 1+\ln x \]

对于这个级数，我们可以通过拉格朗日中值定理 来证明其上界为\(o(\log x)\)级别：

\[\begin{align} &设b<a,由拉格朗日中值定理:\\ \\ &\exists \ \delta\in[b,a]\ 使得 \frac{f(a)-f(b)}{a-b}=f'(\delta)\\ \\ &令 f(x)=\ln x,则f'(x)=\frac{1}{x}\\ \\ &b\leq \delta\leq a,则 \frac{1}{\delta} \geq \frac{1}{a}\\ \\ &令a=n,b=n-1,则: \\ \\ &\ln \frac{n}{n-1}= \frac{\ln n-\ln (n-1)}{n-(n-1)}=\frac{1}{\delta}\geq \frac{1}{n}\\ \\ &\sum_{n=2}^x\ln \frac{n}{n-1}\geq \sum_{n=2}^x \frac{1}{n}\\ \\ &而\sum_{n=2}^ x \ln \frac{n}{n-1}=\ln \left( \prod_{n=2}^x \frac{n}{n-1} \right)=\ln x\\ \\ &\therefore \sum_{n=1}^x \frac{1}{n} =1+\sum_{n=2}^x \frac{1}{n}\leq 1+\ln x \end{align} \]

---

Cut Check Bit

位运算 #数学 #dp #数位dp

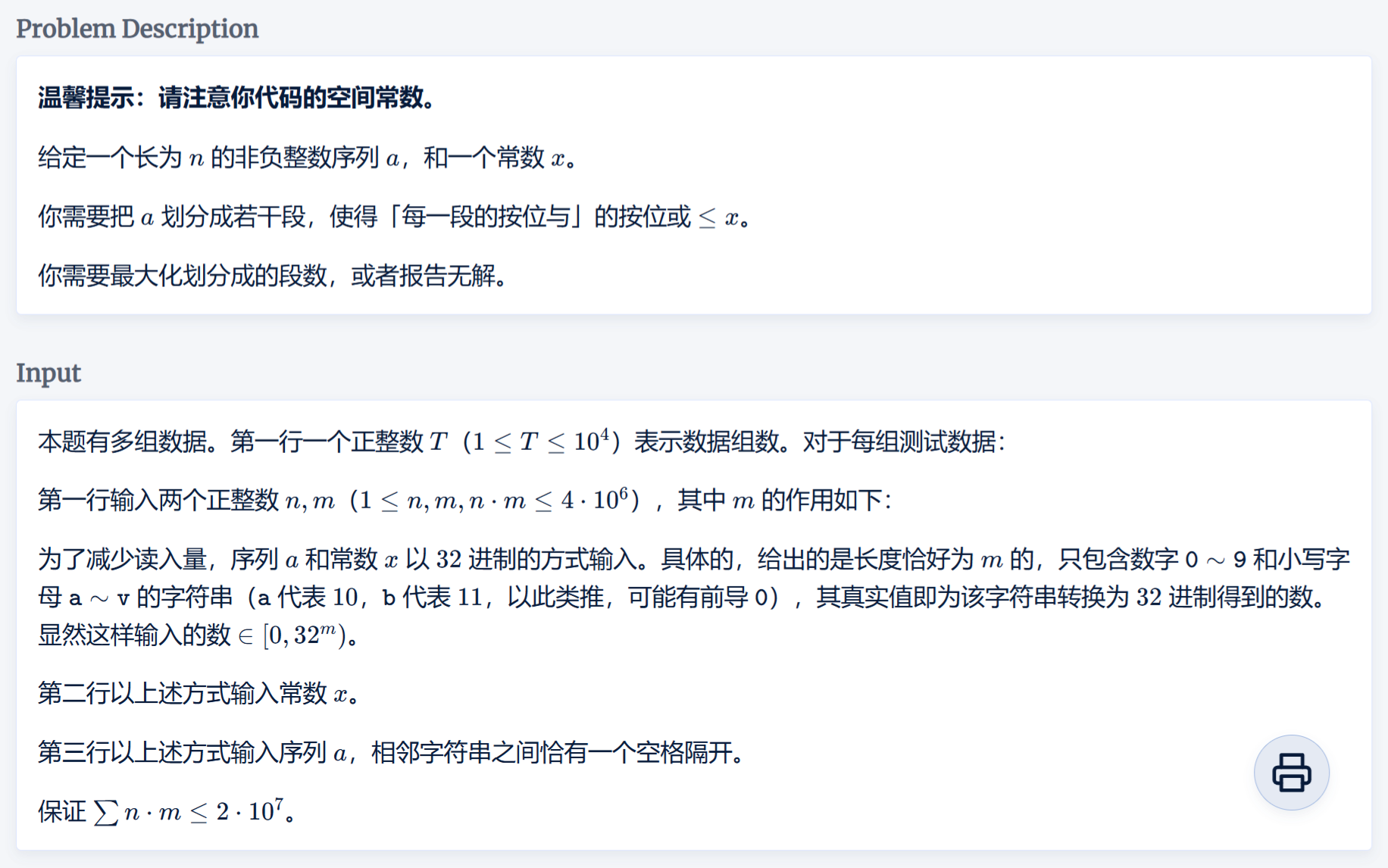
题目

思路

不是很懂为什么官方题解这么简短，莫非出题人是CCB领域大神？！

关于\(2^k\)进制数的特点：

这样的进制数实际上都可以在化为二进制后直接拼接在一起！

比如\(32=2^{5}\)进制的数\(x_{3}x_{2}x_{1}x_{0}(32)=x_{3}\times 32^{3}+x_{2}\times 32^{2}+x_{1}\times 32+x_{0}(10)\)

而一个数乘以\(2^{k}\)就相当于其二进制表示左移\(k\)位，因此直接将\(x_{3}x_{2}x_{1}x_{0}\)所对应的二进制数由高位到低位直接拼接起来即可得到其二进制表示！

题干需要将各个段中的数字相与后再相或，并且还需要小于\(x\)，那么相或后的结果\(t\)就需要满足\(t\ |\ x=x\)，即\(x\)为0的位置上\(t\)必须为0，\(x\)为1的位置上\(t\)没有限制

由于相与的性质，对于一个确定的分段，只要有一个数字在\(pos\)位上是0，那么相与出来的数在\(pos\)位上必然也是0，这就可以作为我们调控\(t\leq x\)的限制

若\(t\leq x\)，则在\(x\)为0的位置上，\(t\)必须也为0；在\(x\)为1的位置上，\(t\)可以为0也可以为1

一个数位dp的技巧：
\(t\leq x\)等价于\(t<x+1\)

为什么要这样做？

• 在\(t\leq x\)的限制下，除了\(t<x\)时可以自由选择，需要额外考虑\(t=x\)时的"紧贴上界"情况
• 而在\(t<x+1\)的限制下，仅需要保证\(t\)严格小于\(x+1\)的情况，不存在"紧贴上界"一说
• 在\(t<x+1\)的限制下，更新时可以一直限制\(t\)当前位为0（后文解释）

创建四个数组用于数位dp：

• \(1\leq i\leq n\)
• \(pre[i]\)表示在处理第\(pos\)位时，\(1\sim i-1\)中距离\(i\)最近的\(0\)的位置，即\((a[\ pre[i]\ ]\gg pos)\&1=0\)；换一种说法，\(pre[i]\)表示仅考虑第\(pos\)位的情况下，以\(i\)位置作为一个段的结尾，这个段的最优左端点在\(pre[i]\)处
• \(l[i]\)表示考虑\(1\sim pos\)位上的限制，处理第\(pos\)位时，以\(i\)位置作为一个段的结尾，这个段的最优左端点在\(r[i]\)处
• \(dp[i]\)表示考虑\(1\sim pos\)位上的限制，处理第位时，\(1\sim i\)的最大分段数
• \(max[i]\)表示在处理第\(pos\)位时，\(1\sim i\)中的最大\(dp\)值

接下来需要理解一些过程：

• 设\(xbit\)为\(x+1\)在第\(pos\)位上的数字，\(tbit\)为段与段的\(OR\)和：\(t\) 在第\(pos\)位上的数字
• 不管\(xbit\)是什么，都先更新\(pre\)数组
• 若\(xbit=0\)，则必须有\(tbit=0\)，此时用\(pre\)数组更新\(l\)数组的限制，但不更新\(dp\)数组
• 若\(xbit=1\)，则必须有\(tbit=0\)（看似与\(t=0 /1\)矛盾），此时\(dp\)数组由\(pre,l\)两个数组共同限制来更新，同时更新全局答案\(ans\)，但\(l\)数组不更新

举一个例子 来辅助理解：
以下数字均采用二进制，左端为高位右端为低位

• 设\(x+1=10010\)
• 由于高位对数字大小的影响更大，所以从高位向低位遍历
• \(pos=5\)时，\(xbit=1\)：
  • 理论上\(tbit=0 /1\)，但是由于比较的是\(x+1\)，\(t\)需要严格小于\(x+1\)，所以\(t=0\)，否则\(t=x=1\)相等了
  • 通过限制\(tbit=0\)，可以更新\(dp\)数组得到一次答案
• \(pos=4、3\)时，\(xbit=0\)：
  • 必须有\(tbit=0\)
  • 通过\(pre\)来更新\(l\)数组的限制
  • 此时不能更新\(dp\)，因为\(x\)与\(t\)在这一位的值都是0，那么便有相等的风险！以\(pos=3\)为例，\(x:100\ ,\ t_{1}:100\ ,t_{2}:000\)，此时更新\(dp\)将把\(t_{1}\)的答案算进去，因此错误
• \(pos=2\)时，\(xbit=1\)：
  • 若\(tbit=1\)，则会出现\(x:1001\ ,\ t_{1}:1000,t_{2}:1001,t_{3}:0001,t_{4}:0000\)四种情况，其中\(t_{2}=x\)非法，再一次验证\(tbit=0\)的正确性
  • 但若限制了\(tbit=0\)，\(t_{3}:0001\)的情况不会漏掉吗？这也是合法的情况呀？
  • 不会漏掉，因为本次不更新\(l\)数组，\(tbit=0\)的限制不会影响到后续的\(pos\)
  • 正如\(pos=5\)时限制了\(tbit=0\)，但是没有更新进\(l\)数组里，所以现在\(pos=2\)时，\(t\)中\(pos=5\)的位置就是\(0 /1\)

伪代码：

从高位向低位遍历\(pos\)：
为了方便，将\(a_{i}\)在\(pos\)位上的值统称为\(i\)的值

• 预处理\(pre[i]\)：
  • 遍历\(1\leq i\leq n\)
  • 若\(i\)的值为0，那么为了使得分段数尽可能多，则段长要尽可能小，因此最优左端点要尽可能靠近右端点，等于右端点是最优的，\(pre[i]=i\)
  • 若\(i\)的值为1，那么只能从\(pre[i-1]\)转移过来，\(pre[i]=pre[i-1]\)
• 若\(xbit=0\)：
  • 遍历\(1\leq i\leq n\)
  • 用\(l\)数组加入\(pre\)的限制：\(l[i]=min\{ l[i],pre[i] \}\)
• 若\(xbit=1\)：
  • 遍历\(1\leq i\leq n\)
  • \(cur=min\{ l[i],pre[i] \}\)，代表最优左端点位置
  • 若\(cur=0\)，说明在当前限制条件下无法分段，\(dp[i]=-1\)
  • 否则\(dp\)由\(cur-1\)的状态转移而来：\(dp[i]=dp[\ max[cur-1]\ ]+1\)
  • \(max[i]=max\{ max[i-1],dp[i] \}\)
  • \(ans=max\{ ans,dp[n] \}\)

最后还需要特判\(x\)二进制为全1的情况，因为此时\(x+1\)只有最高位为1，其他都为0，而这个最高位有可能超出\(m\)的限制导致\(dp\)过程认为\(x+1=00\dots0 0\)出错

因此在\(x\)为全1的时候直接输出\(n\)即可~

代码实现

#include<iostream>
#include<vector>
#include<cmath>
#include<queue>
#include<algorithm>
#include<set>
#include<stack>
#include<unordered_map>
using namespace std;
using ll = long long;
// #define int ll
#define rep(i, a, b) for(int i = (a); i <= (b); i ++)
#define per(i, a, b) for(int i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';


int n, m;
const int inf = 2e14;
bool readx(vector<int>& x) {
    string s;cin >> s;
    int cnt = 0;
    rep(j, 1, m) {
        char c = s[m - j];
        if (c >= 'a')x[j] = c - 'a' + 10;
        else x[j] = c - '0';
        cnt += __builtin_popcount(x[j]);
    }
    if (cnt == 5 * m)return 1;
    int add = 1;
    rep(i, 1, m) {
        x[i] += add;
        add = x[i] / 32;
        x[i] %= 32;
    }
    return 0;
}

void read(vector<vector<int>>& a, int i) {
    string s;cin >> s;
    rep(j, 1, m) {
        char c = s[m - j];
        if (c >= 'a')a[i][j] = c - 'a' + 10;
        else a[i][j] = c - '0';
    }
}

void chmax(int& x, int y) {
    x = max(x, y);
}
void chmin(int& x, int y) {
    x = min(x, y);
}

void see2(int x) {
    vector<int>res(5,0);
    int pos = 0;
    while (x) {
        res[pos++] = (x & 1);
        x >>= 1;
    }
    per(i, 5 - 1, 0)cout << res[i];
}

void eachT() {
    cin >> n >> m;
    vector<vector<int>>a(n + 1, vector<int>(m + 1, 0));
    vector<int>x(m + 1);
    bool flag=readx(x);
    rep(i, 1, n)read(a, i);
    if (flag) { cout << n << '\n'; return; }
    vector<int>l(n + 1), pre(n + 1, 0), dp(n + 1, 0), ma(n + 1, 0);
    rep(i, 1, n)l[i] = i;
    int ans = -1;
    per(p, m, 1) {
        per(pos, 4, 0) {
            rep(j, 1, n) {
                bool bit = (a[j][p] >> pos) & 1;
                pre[j] = bit ? pre[j-1] : j;
            }
            bool xbit = (x[p] >> pos) & 1;
            if (xbit) {
                rep(j, 1, n) {
                    int cur = min(l[j], pre[j]);
                    dp[j] = cur ? ma[cur - 1] + 1 : -1;
                    ma[j] = max(ma[j - 1], dp[j]);
                }
                chmax(ans, dp[n]);
            } else {
                rep(j, 1, n)chmin(l[j], pre[j]);
            }
        }
    }
    cout << ans << '\n';
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    ll t = 1;
    cin >> t;
    while (t--) {
        eachT();
    }
}