【Random Matrices】第一章-随机矩阵入门

Getting Started

• 新手入门
• • • [🔢 特征值计算结果](#🔢 特征值计算结果)
    • [📊 特征值分布可视化](#📊 特征值分布可视化)
    • [💡 现象解读与学习提示](#💡 现象解读与学习提示)
    • [🔬 详细解析三大系综](#🔬 详细解析三大系综)
    • • [1. GUE](#1. GUE)
      • • 共轭转置
      • [2. GSE](#2. GSE)
      • [3. 特征值分布范围公式](#3. 特征值分布范围公式)
    • [🧠 核心概念澄清](#🧠 核心概念澄清)
• 数学笔记：随机变量与概率分布基础
• • 随机变量的定义 (Definitions)
  • 统计性质 (Statistical Moments)
  • 多变量分布 (Multivariate Distributions)
  • 变量变换 (Change of Variables)
• 补充知识
• • [构建 GOE 矩阵的分布](#构建 GOE 矩阵的分布)
  • • [1️⃣原始非对称矩阵 H H H](#1️⃣原始非对称矩阵 H H H)
    • [2️⃣构造实对称矩阵 H s H_s Hs](#2️⃣构造实对称矩阵 H s H_s Hs)
    • 3️⃣非对角元的高斯分布推导
    • • [1. 期望](#1. 期望)
      • [2. 方差](#2. 方差)
      • [3. 分布](#3. 分布)
    • [4️⃣对称矩阵 H s H_s Hs 的 jpdf](#4️⃣对称矩阵 H s H_s Hs 的 jpdf)
    • 5️⃣方差对比的重要性
    • 6️⃣记号的简化

新手入门

首先，我们来看看一个由高斯分布采样得到的6×6的矩阵：

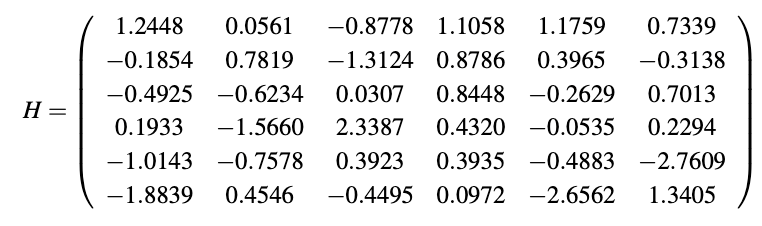
🔢 特征值计算结果

这个6×6矩阵共有6个特征值 ：

📊 特征值分布可视化

为了更直观地理解，下图展示了所有特征值在复平面上的位置：

import numpy as np
import matplotlib.pyplot as plt

# 1. 下载中文字体 (SimHei)
!wget -O SimHei.ttf "https://github.com/StellarCN/scp_zh/raw/master/fonts/SimHei.ttf"

# 2. 配置 Matplotlib 使用该字体
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm

# 将下载的字体添加到 font_manager
fm.fontManager.addfont('SimHei.ttf')

# 设置全局字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题

# 给定矩阵 H
H = np.array([
    [1.2448, 0.0561, -0.8778, 1.1058, 1.1759, 0.7339],
    [-0.1854, 0.7819, -1.3124, 0.8786, 0.3965, -0.3138],
    [-0.4925, -0.6234, 0.0307, 0.8448, -0.2629, 0.7013],
    [0.1933, -1.5660, 2.3387, 0.4320, -0.0535, 0.2294],
    [-1.0143, -0.7578, 0.3923, 0.3935, -0.4883, -2.7609],
    [-1.8839, 0.4546, -0.4495, 0.0972, -2.6562, 1.3405]
])

# 计算特征值
eigenvalues = np.linalg.eigvals(H)

print(eigenvalues)

# 绘制特征值分布
plt.figure(figsize=(8, 6))
# 绘制复平面上的特征值点
plt.scatter(eigenvalues.real, eigenvalues.imag, color='blue', s=100, zorder=5, label='特征值')
# 突出显示实数轴 (x轴) 和虚数轴 (y轴)
plt.axhline(y=0, color='black', linewidth=0.5, linestyle='--', alpha=0.5)
plt.axvline(x=0, color='black', linewidth=0.5, linestyle='--', alpha=0.5)
plt.xlabel('实部')
plt.ylabel('虚部')
plt.title('随机矩阵 H 的特征值在复平面上的分布')
plt.grid(True, linestyle=':', alpha=0.6)
plt.axis('equal')  # 保证比例相同
plt.legend()
plt.show()

（可在Colab中执行此Python代码将生成对应的分布图）

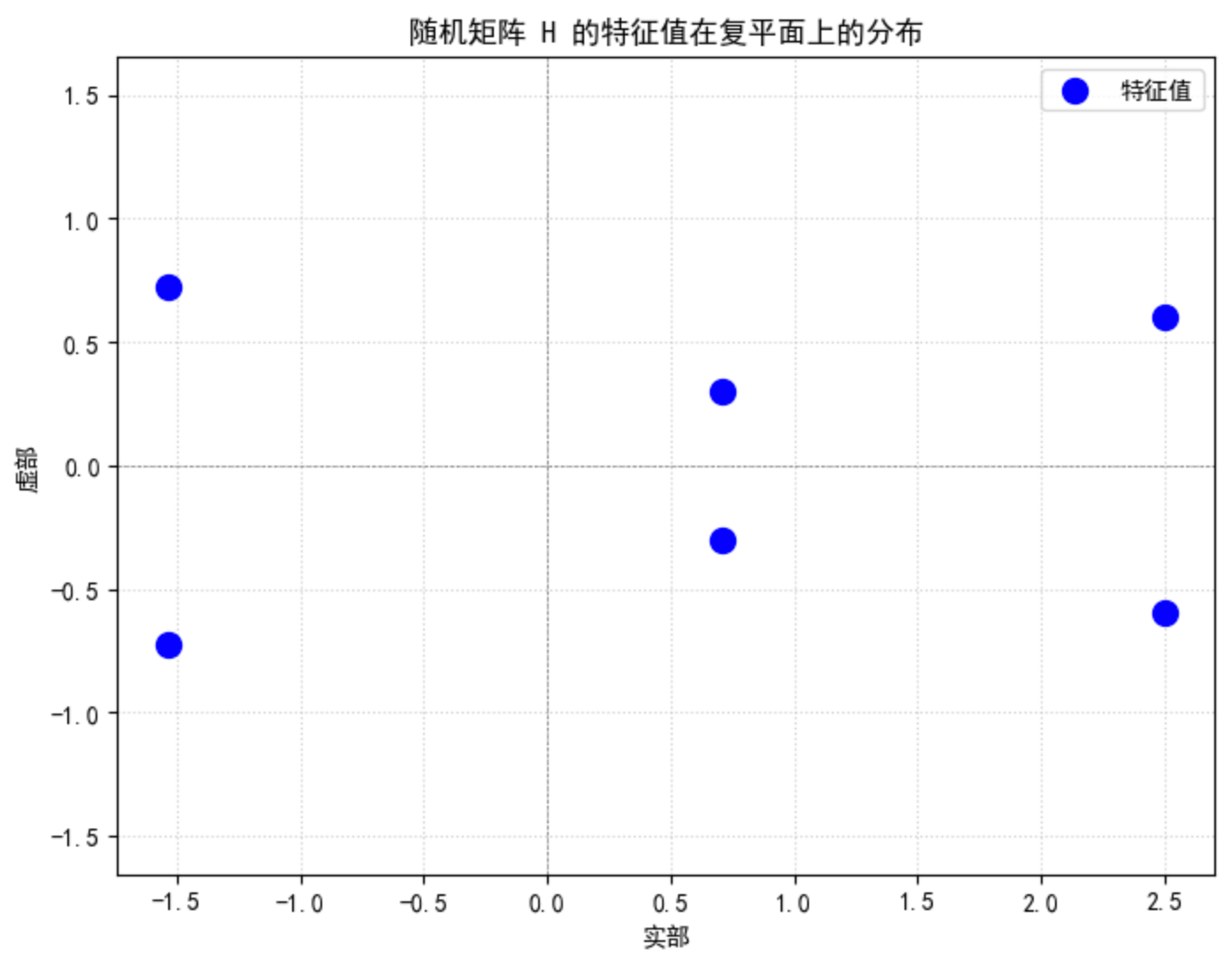
💡 现象解读与学习提示

这个结果恰好展示了非对称随机矩阵的一个典型现象：

1. 特征值可以是复数 ：因为矩阵 H 不是对称矩阵（H ≠ H^T），所以其特征值不一定全是实数，出现了共轭复数对。

对称矩阵 ⟹ 只能是实数。

非对称矩阵 ⟹ 有可能是复数（在随机矩阵理论中，几乎总是复数）。

2. 分布范围 ：这些特征值散落在复平面原点附近。如果这是一个更大规模（如1000×1000）的标准高斯随机矩阵 （元素来自N(0,1)），其特征值通常会近似分布在以原点为圆心、半径约为√n的圆盘内------这就是著名的 Girko圆律（或Circular Law）的体现。

"圆律"代码运行：

import numpy as np
import matplotlib.pyplot as plt

# 1. 设置更大的维度
N = 1000

# 2. 生成非对称的标准高斯随机矩阵 (Real Ginibre Ensemble)
# 这里的 scale=1.0 对应 N(0, 1)
H_large = np.random.normal(loc=0.0, scale=1.0, size=(N, N))

# 3. 计算特征值
eigenvalues = np.linalg.eigvals(H_large)

# 4. 绘图
plt.figure(figsize=(8, 8)) # 正方形画布，方便看圆
plt.scatter(eigenvalues.real, eigenvalues.imag, s=1, alpha=0.6, color='blue', label='特征值')

# 5. 画出理论边界：半径为 sqrt(N) 的圆
theta = np.linspace(0, 2*np.pi, 100)
radius = np.sqrt(N)
x_circ = radius * np.cos(theta)
y_circ = radius * np.sin(theta)
plt.plot(x_circ, y_circ, 'r--', linewidth=2, label=f'理论边界 (R=√{N:.0f})')

plt.axhline(y=0, color='black', linewidth=0.5, alpha=0.5)
plt.axvline(x=0, color='black', linewidth=0.5, alpha=0.5)
plt.title(f'Girko圆律验证 (N={N})')
plt.xlabel('实部')
plt.ylabel('虚部')
plt.legend(loc='upper right')
plt.axis('equal') # 保证横纵比例一致，不然圆会变椭圆
plt.show()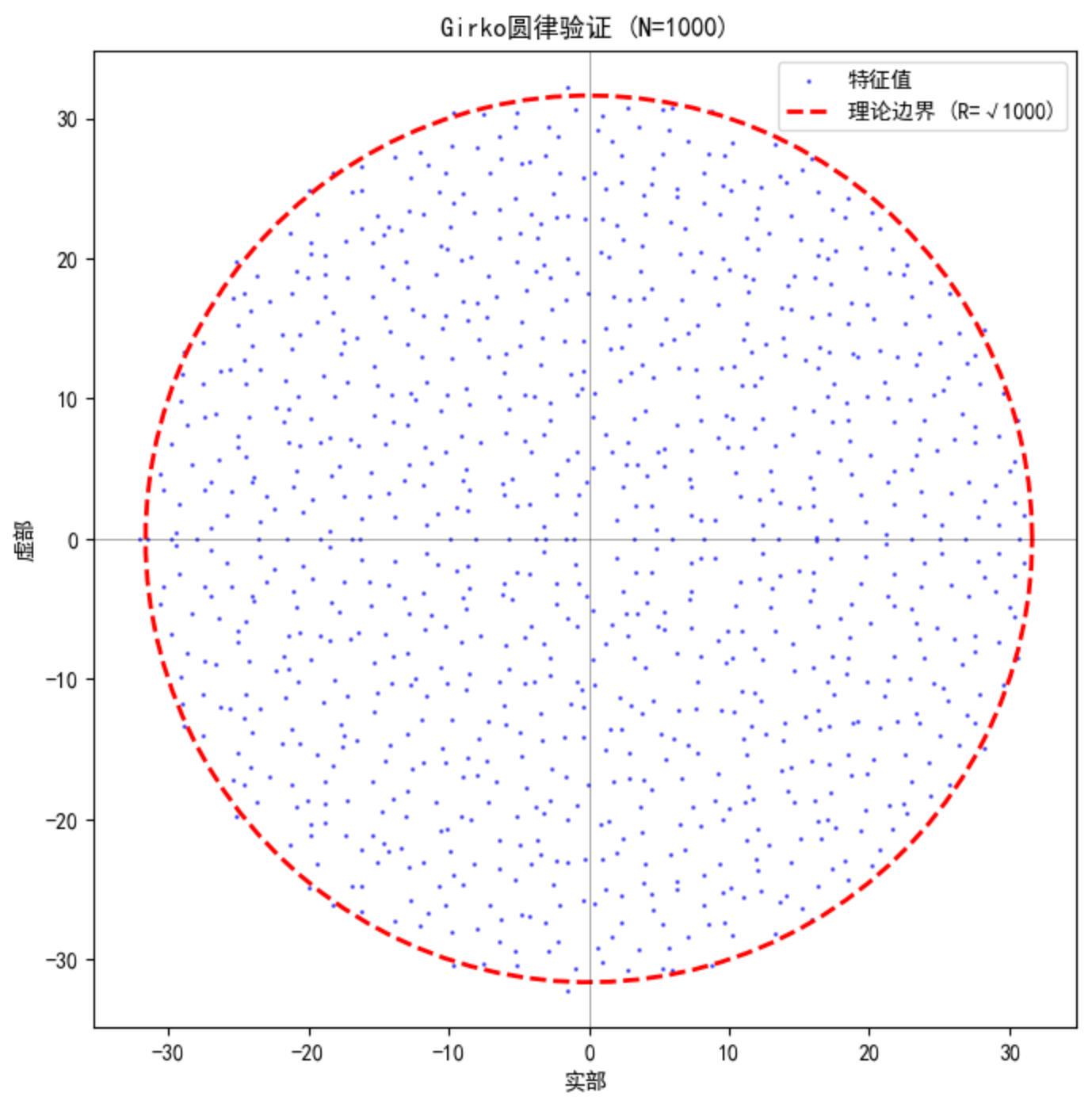

接下来，进一步探索计算这个矩阵的对称化版本 H_s = (H + H^T)/2 的特征值。

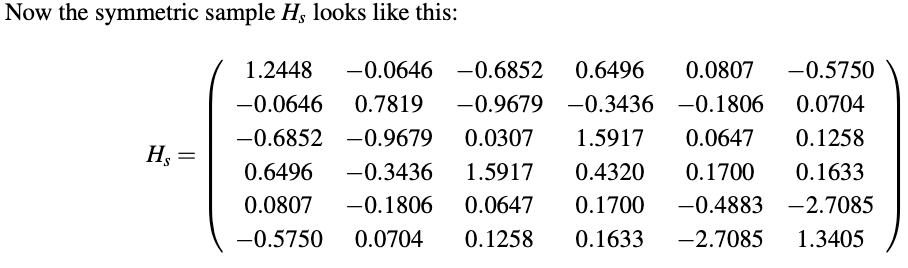
它的特征值为：{−2.49316,−1.7534, 0.33069, 1.44593, 2.38231, 3.42944}

这就是GOE (Gaussian Orthogonal Ensemble)

如何构造一个GOE矩阵？

最简单的构造方法是：先生成一个 n×n 的标准高斯随机矩阵 G（每个元素 Gᵢⱼ ~ N(0, 1)），然后将其对称化。

接下来介绍随机矩阵理论"三大经典系综"：

为了直观理解三大系综的关系与核心区别，将其总结为下表：

特性	GOE (高斯正交系综)	GUE (高斯酉系综)	GSE (高斯辛系综)
矩阵类型	实对称矩阵	复厄米特矩阵	四元数自对偶矩阵
元素要求	A = A^⊤，元素为实数	A = A^†，元素为复数	满足自对偶条件
不变性	正交变换	酉变换	辛变换
特征值	全是实数	全是实数	全是实数
特征值分布范围	[-√(2N), √(2N)]	[-√(4N), √(4N)]	[-√(8N), √(8N)]
物理系统	有时间反演对称（自旋无关）	无时间反演对称	有时间反演对称（自旋有关）

🔬 详细解析三大系综

1. GUE

例子 H_her 是一个 2×2 的复厄米特矩阵：

H_her = [ 0.3252,     0.3077 + 0.2803i;
          0.3077 - 0.2803i,    -1.7115 ]

关键特征：

• 对角线元素是实数（0.3252, -1.7115）
• 非对角线元素互为复共轭（0.3077+0.2803i 和 0.3077-0.2803i）
• 满足 A = A^†（厄米特条件），其中 † 表示共轭转置
• 特征值全是实数（可计算验证）

Python验证：

import numpy as np

H_her = np.array([[0.3252, 0.3077+0.2803j],
                  [0.3077-0.2803j, -1.7115]])

# 检查是否为厄米特矩阵
print("H == H†?", np.allclose(H_her, H_her.conj().T))

# 计算特征值
eigvals = np.linalg.eigvalsh(H_her)  # 专用于厄米特/对称矩阵
print("特征值 (实数):", eigvals)

H == H†? True

特征值 (实数): [-1.79327913 0.40697913]

共轭转置

"共轭转置"（Conjugate Transpose）其实就是两个动作的组合："转置" + "共轭"。

在 Python 代码 H_her.conj().T 中：
.T 代表 转置 (Transpose)
.conj() 代表 共轭 (Conjugate)

这两个动作不分先后（先转置再共轭，或者先共轭再转置，结果是一样的）。

为了看懂，我们用提供的这个 2 × 2 2 \times 2 2×2 矩阵一步步拆解：

假设矩阵 H H H 为：

H = [ 0.3252 0.3077 + 0.2803 i 0.3077 − 0.2803 i − 1.7115 ] H = \begin{bmatrix} 0.3252 & \color{blue}{0.3077 + 0.2803i} \\ \color{red}{0.3077 - 0.2803i} & -1.7115 \end{bmatrix} H=[0.32520.3077−0.2803i0.3077+0.2803i−1.7115]

第一步：转置 (Transpose)

规则：沿对角线翻转，把行变成列，列变成行。

对角线上的元素（ 0.3252 0.3252 0.3252 和 − 1.7115 -1.7115 −1.7115）位置不动。

右上角的元素（蓝色）和左下角的元素（红色）互换位置。

转置后的矩阵 H T H^T HT：
H T = [ 0.3252 0.3077 − 0.2803 i 0.3077 + 0.2803 i − 1.7115 ] H^T = \begin{bmatrix} 0.3252 & \color{red}{0.3077 - 0.2803i} \\ \color{blue}{0.3077 + 0.2803i} & -1.7115 \end{bmatrix} HT=[0.32520.3077+0.2803i0.3077−0.2803i−1.7115]

(注意：现在右上角变成了减号，左下角变成了加号，因为它们换了位置)

第二步：共轭 (Conjugate)

规则：把所有虚数前面的符号"取反"（ + + + 变 − - −， − - − 变 + + +）。实数部分不变。

对刚才的 H T H^T HT 进行共轭操作：

右上角 0.3077 − 0.2803 i \color{red}{0.3077 - 0.2803i} 0.3077−0.2803i → 变号 \xrightarrow{\text{变号}} 变号 0.3077 + 0.2803 i 0.3077 + 0.2803i 0.3077+0.2803i

左下角 0.3077 + 0.2803 i \color{blue}{0.3077 + 0.2803i} 0.3077+0.2803i → 变号 \xrightarrow{\text{变号}} 变号 0.3077 − 0.2803 i 0.3077 - 0.2803i 0.3077−0.2803i

对角线是实数，没有虚部，保持不变。

得到最终的共轭转置矩阵 H † H^\dagger H†：
H † = [ 0.3252 0.3077 + 0.2803 i 0.3077 − 0.2803 i − 1.7115 ] H^\dagger = \begin{bmatrix} 0.3252 & 0.3077 + 0.2803i \\ 0.3077 - 0.2803i & -1.7115 \end{bmatrix} H†=[0.32520.3077−0.2803i0.3077+0.2803i−1.7115]

结论：神奇的事情发生了

请对比一下最初的 H H H 和最后算出来的 H † H^\dagger H†：

最初的 H: [ 0.3252 0.3077 + 0.2803 i 0.3077 − 0.2803 i − 1.7115 ] \begin{bmatrix} 0.3252 & 0.3077 + 0.2803i \\ 0.3077 - 0.2803i & -1.7115 \end{bmatrix} [0.32520.3077−0.2803i0.3077+0.2803i−1.7115]

结果 H†: [ 0.3252 0.3077 + 0.2803 i 0.3077 − 0.2803 i − 1.7115 ] \begin{bmatrix} 0.3252 & 0.3077 + 0.2803i \\ 0.3077 - 0.2803i & -1.7115 \end{bmatrix} [0.32520.3077−0.2803i0.3077+0.2803i−1.7115]

你会发现 H H H 完全等于 H † H^\dagger H†。

这就是代码里 np.allclose(H_her, H_her.conj().T) 返回 True 的原因。满足这个条件的矩阵（自己等于自己的共轭转置），就叫 厄米特矩阵 (Hermitian Matrix)。

总结它的性质：

厄米特矩阵就像是复数世界里的"对称矩阵"。正因为这种特殊的对称性（转置后变了位置，但共轭后又变回了原样），它保证了特征值一定是实数。

2. GSE

在随机矩阵理论（RMT）的大家族中，GSE (Gaussian Symplectic Ensemble，高斯辛系综) 是"三大经典系综"中的第三个成员。

GSE 是最"高冷"的一个，因为它涉及到一个特殊的数学结构------四元数 (Quaternions)。

什么是四元数？ 普通的复数是 α + bi，四元数则是 α + bi 十 cj + dk。 在矩阵表示中，一个四元数通常被写成一个 2 × 2 的复数矩阵。因此，一个 N × N 的四元数矩阵，在计算机里通常被处理成一个 2N ×2N 的复矩阵。

最显著的特征：克拉默简并 (Kramers Degeneracy)

这是 GSE 和 GOE/GUE 最大的区别，一眼就能认出来：

GSE 的所有特征值都是成对出现的（重数为 2）。

每一对特征值完全相等。这在物理上被称为 克拉默简并 (Kramers Degeneracy)

例如：

某个GSE (10x10) 的特征值：
[-8.3815  -8.3815  -4.7798  -4.7798  -0.4396  -0.4396   2.9635   2.9635   4.7203  4.7203]
特征值差异 (Diff):
[0.     3.6017      0.     4.3403     0.     3.4031    0.     1.7568   0.    ]

这里交替出现的 0验证了 GSE 最核心的两个特征：克拉默简并 (Kramers Degeneracy) 和 能级排斥 (Level Repulsion)。

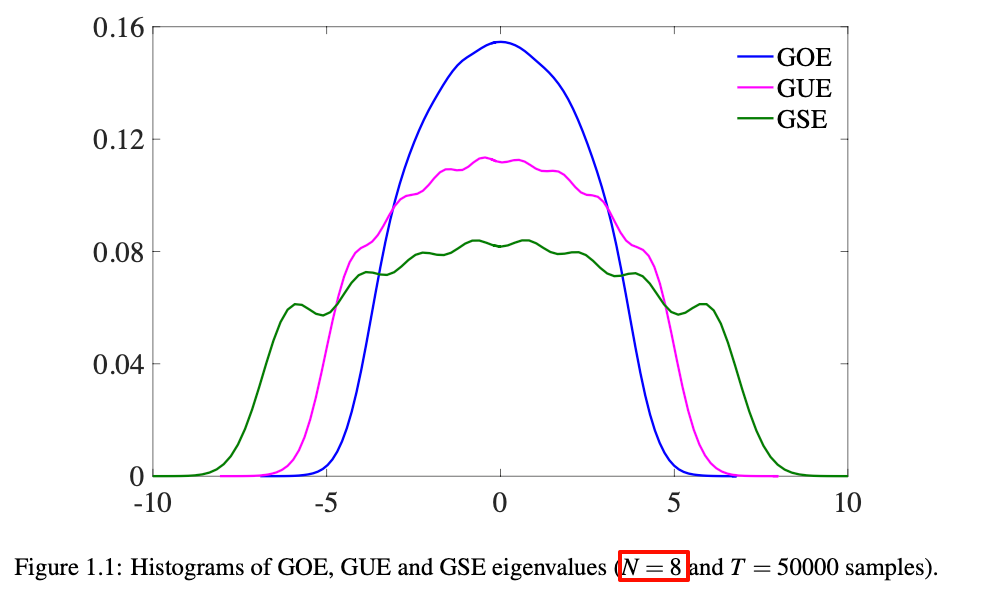
3. 特征值分布范围公式

系综	特征值范围	对N=8的计算
GOE	±√(2N)	±√(2×8) = ±√16 = ±4
GUE	±√(4N)	±√(4×8) = ±√32 ≈ ±5.66
GSE	±√(8N)	±√(8×8) = ±√64 = ±8

其特征值分布如下图所示：

🧠 核心概念澄清

• GOE不含正交矩阵 ：它包含的是实对称矩阵
• 特征值全为实数：这是对称/厄米特/自对偶矩阵的数学性质
• 统计需要大量样本：单个矩阵的特征值只是随机样本，需要大量样本才能看到统计规律

---

数学笔记：随机变量与概率分布基础

随机变量的定义 (Definitions)

本质 ：随机变量 X X X 既不是"随机"也不是"变量"，它本质上是一个函数。

类型 ：

离散型 (Discrete)：取值在有限集合中，如掷骰子 { 1 , ... , 6 } \{1, \dots, 6\} {1,...,6}。

连续型 (Continuous)：取值在实数轴的区间 σ \sigma σ 上。

概率密度函数 (PDF) ：记为 ρ ( x ) \rho(x) ρ(x)。

定义： X X X 落在区间 ( a , b ) (a, b) (a,b) 的概率为 ∫ a b ρ ( x ) d x \int_a^b \rho(x) dx ∫abρ(x)dx。

归一化 (Normalization)：全概率之和必须为 1。

∫ σ ρ ( x ) d x = 1 \int_{\sigma} \rho(x) dx = 1 ∫σρ(x)dx=1

例子：高斯分布 (Normal distribution) N ( μ , σ 2 ) N(\mu, \sigma^2) N(μ,σ2) 的 PDF 为 ρ ( x ) = 1 2 π σ exp ⁡ ( − ( x − μ ) 2 2 σ 2 ) \rho(x) = \frac{1}{\sqrt{2\pi}\sigma} \exp(-\frac{(x-\mu)^2}{2\sigma^2}) ρ(x)=2π σ1exp(−2σ2(x−μ)2)。

统计性质 (Statistical Moments)

一旦有了 PDF，可以通过积分计算分布的关键特征：

期望/均值 (Mean/Expectation)：分布的中心。

⟨ X ⟩ = ∫ x ρ ( x ) d x \langle X \rangle = \int x \rho(x) dx ⟨X⟩=∫xρ(x)dx

高阶矩 (Higher Moments)：

⟨ X n ⟩ = ∫ x n ρ ( x ) d x \langle X^n \rangle = \int x^n \rho(x) dx ⟨Xn⟩=∫xnρ(x)dx

方差 (Variance)：衡量分布的离散程度（宽度）。

Var ( X ) = ⟨ X 2 ⟩ − ⟨ X ⟩ 2 \text{Var}(X) = \langle X^2 \rangle - \langle X \rangle^2 Var(X)=⟨X2⟩−⟨X⟩2

累积分布函数 (CDF)： X ≤ x X \le x X≤x 的概率。

F ( x ) = ∫ − ∞ x ρ ( y ) d y F(x) = \int_{-\infty}^x \rho(y) dy F(x)=∫−∞xρ(y)dy

性质： x → − ∞ x \to -\infty x→−∞ 时 F ( x ) → 0 F(x) \to 0 F(x)→0； x → + ∞ x \to +\infty x→+∞ 时 F ( x ) → 1 F(x) \to 1 F(x)→1。

多变量分布 (Multivariate Distributions)

考虑 N N N 个随机变量 { x 1 , ... , x N } \{x_1, \dots, x_N\} {x1,...,xN}：

联合概率密度 (Joint PDF)： ρ ( x 1 , ... , x N ) \rho(x_1, \dots, x_N) ρ(x1,...,xN)。描述所有变量同时取特定值的概率密度。

独立性 (Independence)：

若变量相互独立，联合 PDF 可分解 (Factorize) 为单变量 PDF 的乘积：

ρ ( x 1 , ... , x N ) = ∏ i = 1 N ρ i ( x i ) \rho(x_1, \dots, x_N) = \prod_{i=1}^N \rho_i(x_i) ρ(x1,...,xN)=i=1∏Nρi(xi)

例子：文中提到的矩阵 H H H 的元素如果是独立高斯变量，其联合分布就是所有元素高斯分布的乘积。

边缘分布 (Marginal PDF)：

只关注其中一个变量（如 x 1 x_1 x1），需要对其他所有变量（ x 2 , ... , x N x_2, \dots, x_N x2,...,xN）进行积分（Integrate out）：

ρ ( x 1 ) = ∫ d x 2  ⁣ ⋯ ∫ d x N ρ ( x 1 , x 2 , ... , x N ) \rho(x_1) = \int dx_2 \dots \int dx_N \rho(x_1, x_2, \dots, x_N) ρ(x1)=∫dx2⋯∫dxNρ(x1,x2,...,xN)

变量变换 (Change of Variables)

当变量发生变换 x i = x i ( y ) x_i = x_i(\mathbf{y}) xi=xi(y) 时，概率密度函数如何变化？

基本原理：概率质量在变换前后守恒，即 ρ ( x ) d x = ρ ( y ) d y \rho(\mathbf{x}) d\mathbf{x} = \rho(\mathbf{y}) d\mathbf{y} ρ(x)dx=ρ(y)dy。

变换公式：

ρ ( x 1 , ... , x N ) d x 1 ... d x N = ρ ( y 1 , ... , y N ) ∣ J ( x → y ) ∣ d y 1 ... d y N \rho(x_1, \dots, x_N) dx_1 \dots dx_N = \rho(y_1, \dots, y_N) |J(\mathbf{x} \to \mathbf{y})| dy_1 \dots dy_N ρ(x1,...,xN)dx1...dxN=ρ(y1,...,yN)∣J(x→y)∣dy1...dyN

整理得新分布 ρ ^ ( y ) \hat{\rho}(\mathbf{y}) ρ^(y)：

ρ ^ ( y ) = ρ ( x ( y ) ) ⋅ ∣ det ⁡ ( J ) ∣ \hat{\rho}(\mathbf{y}) = \rho(\mathbf{x}(\mathbf{y})) \cdot |\det(J)| ρ^(y)=ρ(x(y))⋅∣det(J)∣

雅可比行列式 (Jacobian)：用于修正体积/面积的拉伸或压缩。

J ( x → y ) = det ⁡ ( ∂ x i ∂ y j ) J(\mathbf{x} \to \mathbf{y}) = \det \left( \frac{\partial x_i}{\partial y_j} \right) J(x→y)=det(∂yj∂xi)

好的，我们先把这段内容整理成清晰的数学笔记。它讨论的是实对称随机矩阵 ( H_s ) 的联合概率密度函数（jpdf）推导。

---

补充知识

当你把一个矩阵强行变成对称矩阵（Symmetric Matrix）时，非对角线元素的方差变小了。

因为对称矩阵的非对角线元素是由两个独立的数取平均得来的，这个"取平均"的操作抵消了一部分随机波动，使得它们的分布更集中（方差减半）。

接下来构建 GOE (Gaussian Orthogonal Ensemble) 矩阵的分布来看看这个"反直觉"的现象。

构建 GOE 矩阵的分布

在随机矩阵理论（RMT）中，一个重要的集合是 高斯正交系综（GOE），它由 N x N 的实对称矩阵构成，矩阵元是某种高斯随机变量。

1️⃣原始非对称矩阵 H H H

• 每个矩阵元 H i j H_{ij} Hij ( i , j = 1 , ... , N ( i,j=1,\dots,N (i,j=1,...,N）是 独立 的，且服从标准正态分布：
  H i j ∼ N ( 0 , 1 ) , ρ ( H i j ) = 1 2 π e − H i j 2 / 2 H_{ij} \sim N(0,1), \quad \rho(H_{ij}) = \frac{1}{\sqrt{2\pi}} e^{-H_{ij}^2/2} Hij∼N(0,1),ρ(Hij)=2π 1e−Hij2/2
• 独立随机变量 ⇒ 联合概率密度函数为乘积：
  ρ [ H ] = ∏ i , j = 1 N 1 2 π e − H i j 2 / 2 \rho[H] = \prod_{i,j=1}^N \frac{1}{\sqrt{2\pi}} e^{-H_{ij}^2/2} ρ[H]=i,j=1∏N2π 1e−Hij2/2

2️⃣构造实对称矩阵 H s H_s Hs

我们要从 H H H 构造一个实对称矩阵：
H s = H + H T 2 H_s = \frac{H + H^T}{2} Hs=2H+HT

即：
( H s ) i j = { H i i , i = j H i j + H j i 2 , i ≠ j (H_s){ij} = \begin{cases} H{ii}, & i=j \\ \frac{H_{ij} + H_{ji}}{2}, & i \ne j \end{cases} (Hs)ij={Hii,2Hij+Hji,i=ji=j

注意：

• 对角元直接就是 H i i H_{ii} Hii。
• 非对角元是两个独立高斯变量之和的一半。

3️⃣非对角元的高斯分布推导

已知：
H i j ∼ N ( 0 , 1 ) , H j i ∼ N ( 0 , 1 ) H_{ij} \sim N(0,1), \quad H_{ji} \sim N(0,1) Hij∼N(0,1),Hji∼N(0,1)

两者独立。

对于 i < j i<j i<j，定义：
X i j = H i j + H j i 2 X_{ij} = \frac{H_{ij} + H_{ji}}{2} Xij=2Hij+Hji

这是两个独立同分布高斯变量的线性组合。

---

1. 期望

E [ X i j ] = 1 2 ( E [ H i j ] + E [ H j i ] ) = 0 \mathbb{E}[X_{ij}] = \frac{1}{2} (\mathbb{E}[H_{ij}] + \mathbb{E}[H_{ji}]) = 0 E[Xij]=21(E[Hij]+E[Hji])=0

2. 方差

V a r ( X i j ) = 1 4 [ V a r ( H i j ) + V a r ( H j i ) ] = 1 4 ( 1 + 1 ) = 1 2 \mathrm{Var}(X_{ij}) = \frac{1}{4} \left[ \mathrm{Var}(H_{ij}) + \mathrm{Var}(H_{ji}) \right] = \frac{1}{4} (1 + 1) = \frac{1}{2} Var(Xij)=41[Var(Hij)+Var(Hji)]=41(1+1)=21

3. 分布

X i j ∼ N ( 0 , 1 2 ) X_{ij} \sim N\left(0, \frac{1}{2}\right) Xij∼N(0,21)

因此概率密度函数为：
ρ i j ( x ) = 1 π e − x 2 \rho_{ij}(x) = \frac{1}{\sqrt{\pi}} e^{-x^2} ρij(x)=π 1e−x2

因为对于高斯分布 N ( 0 , σ 2 ) N(0, \sigma^2) N(0,σ2)，密度为 1 2 π σ 2 e − x 2 / ( 2 σ 2 ) \frac{1}{\sqrt{2\pi\sigma^2}} e^{-x^2/(2\sigma^2)} 2πσ2 1e−x2/(2σ2)，此处 σ 2 = 1 / 2 \sigma^2 = 1/2 σ2=1/2，代入得到：
1 2 π ⋅ 1 2 e − x 2 / ( 2 ⋅ 1 2 ) = 1 π e − x 2 \frac{1}{\sqrt{2\pi \cdot \frac12}} e^{-x^2 / (2 \cdot \frac12)} = \frac{1}{\sqrt{\pi}} e^{-x^2} 2π⋅21 1e−x2/(2⋅21)=π 1e−x2

---

4️⃣对称矩阵 H s H_s Hs 的 jpdf

因为对角元和上三角非对角元（ i < j i<j i<j）相互独立（注意：这里独立性需要小心推导，但GOE的定义就是对角元和上三角非对角元相互独立，且各自独立同分布于对应的高斯），所以它们的联合概率密度是乘积形式。

• 对角元个数： N N N，每个分布为 N ( 0 , 1 ) N(0,1) N(0,1)，密度： 1 2 π e − ( H s ) i i 2 / 2 \frac{1}{\sqrt{2\pi}} e^{-(H_s)_{ii}^2/2} 2π 1e−(Hs)ii2/2。
• 上三角非对角元个数： N ( N − 1 ) / 2 N(N-1)/2 N(N−1)/2，每个分布为 N ( 0 , 1 / 2 ) N(0, 1/2) N(0,1/2)，密度： 1 π e − ( H s ) i j 2 \frac{1}{\sqrt{\pi}} e^{-(H_s)_{ij}^2} π 1e−(Hs)ij2。

因此：
ρ [ ( H s ) 11 , ... , ( H s ) N N ] = ∏ i = 1 N 1 2 π e − ( H s ) i i 2 / 2 ∏ i < j 1 π e − ( H s ) i j 2 \boxed{\rho[(H_s){11}, \dots, (H_s){NN}] = \prod_{i=1}^N \frac{1}{\sqrt{2\pi}} e^{-(H_s){ii}^2/2} \prod{i<j} \frac{1}{\sqrt{\pi}} e^{-(H_s)_{ij}^2}} ρ[(Hs)11,...,(Hs)NN]=i=1∏N2π 1e−(Hs)ii2/2i<j∏π 1e−(Hs)ij2

---

5️⃣方差对比的重要性

• 对角元方差 = 1
• 非对角元方差 = 1/2
  所以非对角元方差是对角元方差的 一半。

这个因子 2 2 2差异会影响矩阵特征值的分布、极值统计等，会在后续章节中有重要推论。

6️⃣记号的简化

在实对称矩阵 H s H_s Hs 的上下文中，通常用 ρ [ H ] \rho[H] ρ[H] 表示上三角元（包括对角）的联合概率密度函数，省略下标 s s s 以避免混淆。

总结 ：

（1）GOE矩阵的对称化过程使得非对角元的方差变为对角元的一半，反映在jpdf中的归一化系数不同（ 2 π \sqrt{2\pi} 2π 对 π \sqrt{\pi} π ），指数部分也不同（ e − x 2 / 2 e^{-x^2/2} e−x2/2 对 e − x 2 e^{-x^2} e−x2）。

（2）写联合概率密度（jpdf）时，不能把所有元素一视同仁，对角线和非对角线必须分开写不同的高斯分布公式。