移动零【三种思路】

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意，必须在不复制数组的情况下原地对数组进行操作。

示例 1:

输入: nums = $0,1,0,3,12$

输出: $1,3,12,0,0$

示例 2:

输入: nums = $0$

输出: $0$

LeetCode链接：https://leetcode.cn/problems/move-zeroes/description/

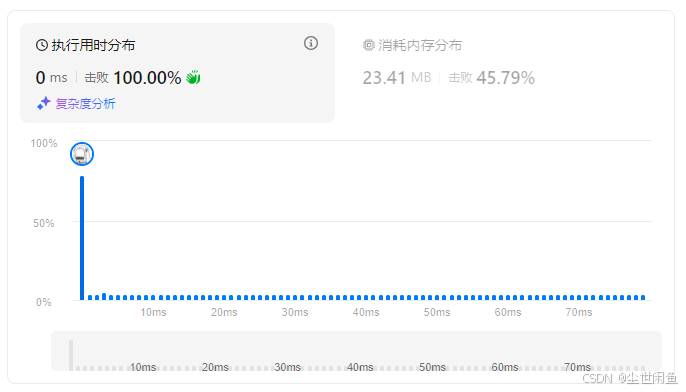
思路一：

双层循环。外层循环找到0的位置，内层循环找到后面最近的非零位置，然后进行替换。

优点：占用空间少，除了两层for循环的计数以外，不占用新的空间。

缺点：双层for循环导致时间复杂度为n² 。

cpp 复制代码

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        for (int i = 0; i < nums.size() - 1; i++) {
            if (0 != nums[i])
                continue;

            for (int j = i + 1; j < nums.size(); j++) {
                if (0 == nums[j])
                    continue;
                else {
                    nums[i] = nums[j];
                    nums[j] = 0;
                    break;
                }
            }
        }
    }
};

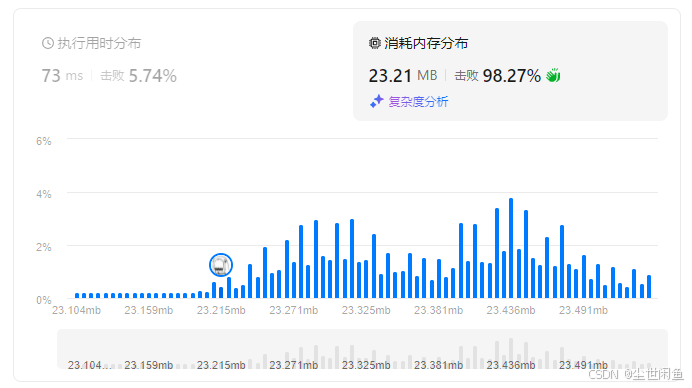
思路二：

不用移动零，只需删除零然后在末尾添加零即可。

优点：时间复杂度为O(n)。

缺点：对vector数组的删除、插入比较费时。且占用有额外空间，

cpp 复制代码

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        if (1 == nums.size()) {
            return;
        }

        int i = 0;
        for (int j = 0; j < nums.size(); j++) {
            if (0 != nums[i]) {
                i++;
                continue;
            }

            nums.erase(nums.begin() + i);
            nums.push_back(0);
        }
    }
};

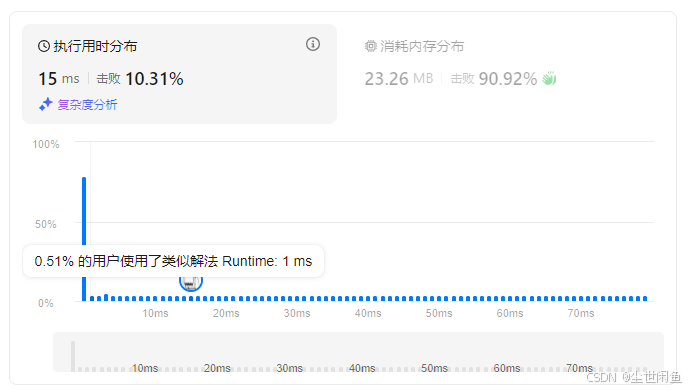
思路三：

插入排序，即保持前L个位置没有零，第R个为零时进行替换。

优点：时间复杂度为O(n)，操作用时短。

缺点：额外占用空间。

cpp 复制代码

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int L=0, R=0;
        while(R<nums.size()){
            if(nums[R] != 0){
                // nums[L] = nums[R];
                // 这里必须要用swap，因为初始时L=R=0，这会导致两种情况：
                // 1、初始位置不为零
                // 2、初始位置为零
                swap(nums[L], nums[R]);
                L++;
            }
            R++;
        }
    }
};