你好呀,我是歪歪。
五年前,我写了一篇关于平滑加权轮询负载均衡策略的算法。
那是我第一次接触到平滑加权轮询负载均衡策略,最后结果呈现出"平滑"的轮询效果之后,我感觉非常厉害。
但是,在当年的文章中有这样的一句话:
我想了很久,我还是不知道背后的数学原理是什么。

由于印象过于深刻,所以五年过去了,关于这个问题,不能说日思夜想吧,但也是念念不忘。
最近一次这个问题再次浮现在脑海中的时候,我决定再次对这个问题发起冲锋。
在参考资料以及 DeepSeek 的加持下,这次终于算是"知其然,也知其所以然"了。
不平滑的加权轮询
在说平滑的加权轮询之前,我们还是得用两三句话简单铺垫一下啥是不平衡的加权轮询,方便后面对比。
举个例子。
假设 A,B,C 三台服务器的权重分别为 5:1:1。
如果是不平滑的加权轮询,最终的执行顺序会是这样的:

会连续选择出权重高的节点,主打一个忙的忙死,闲的闲死。
这样就显得不平滑。
平滑的加权轮询
如果是平滑的加权轮询,它的处理请求的过程是这样的:
假设每个节点有两个权重:
- 一个是配置的 weight,不会变化。
- 一个是 currentWeight 会动态调整,初始值为 0。
每次请求进来,选择节点的时候,按照以下三步执行:
- 遍历节点列表,让每个节点的 currentWeight 都加上自身权重。
- 然后所有节点中,谁的 currentWeight 最大,谁就会被选中。
- 被选中后,将选中节点的 currentWeight 减去权重总和。
上面的逻辑非常简单。
接下来我就配合大量的图片,带着你一步步的推演一下这个过程。
还是以 A:B:C=5:1:1 为例。
我们回到这句话中:
markdown
假设每个节点有两个权重:
* 一个是配置的 weight,不会变化。
* 一个是 currentWeight 会动态调整,初始值为 0。那么最开始,这三个节点,每个节点:
- 配置的 weight 为 A:B:C=5:1:1。
- currentWeight 为 A:B:C=0:0:0。
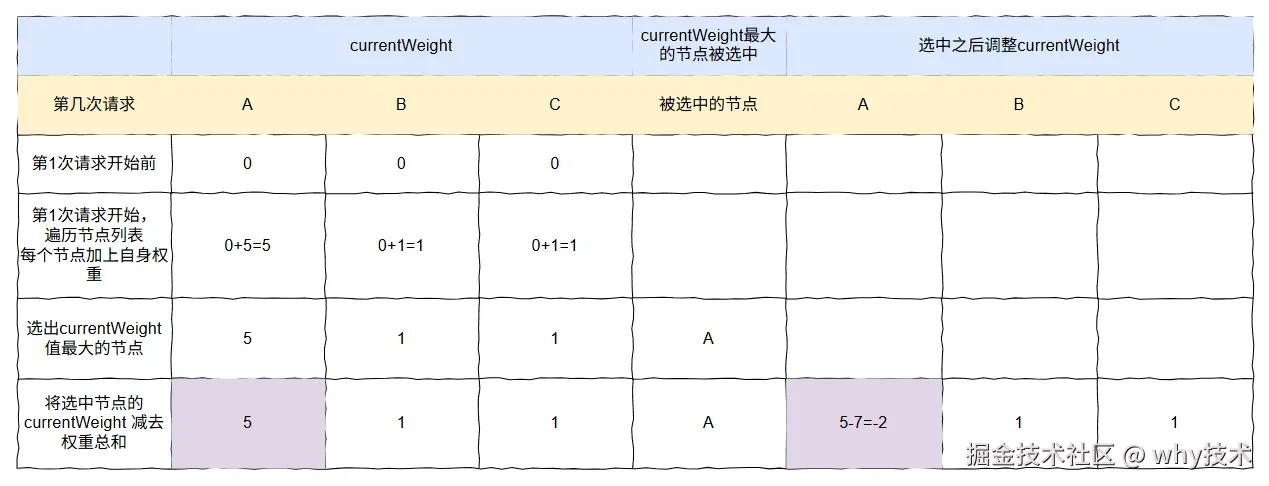
第一次请求
第一次请求进来了,第一步会干啥?
遍历节点列表,让每个节点的 currentWeight 都加上自身权重。
所以,此时 currentWeight 从 A:B:C=0:0:0 变成 A:B:C=5:1:1。
紧接着干啥?
然后所有节点中,谁的 currentWeight 最大,谁就会被选中。
那肯定是 A 的 currentWeight 最大,因为它是 5,另外两个都是 1。
所以,第一次请求,会让 A 节点来处理。
但是,别忘了,还有关键的一步:
被选中后,将选中节点的 currentWeight 减去权重总和。
由于 A 被选中了,所以它的 currentWeight= 5-7=-2。
其中的 7 是 A、B、C 的总权重。
所以,第一次请求过后。
每个节点的 currentWeight 为 A:B:C=-2:1:1。
按照上面的描述,我们画个步骤图:
如果只看最后结果,就是这样的:

第二次请求
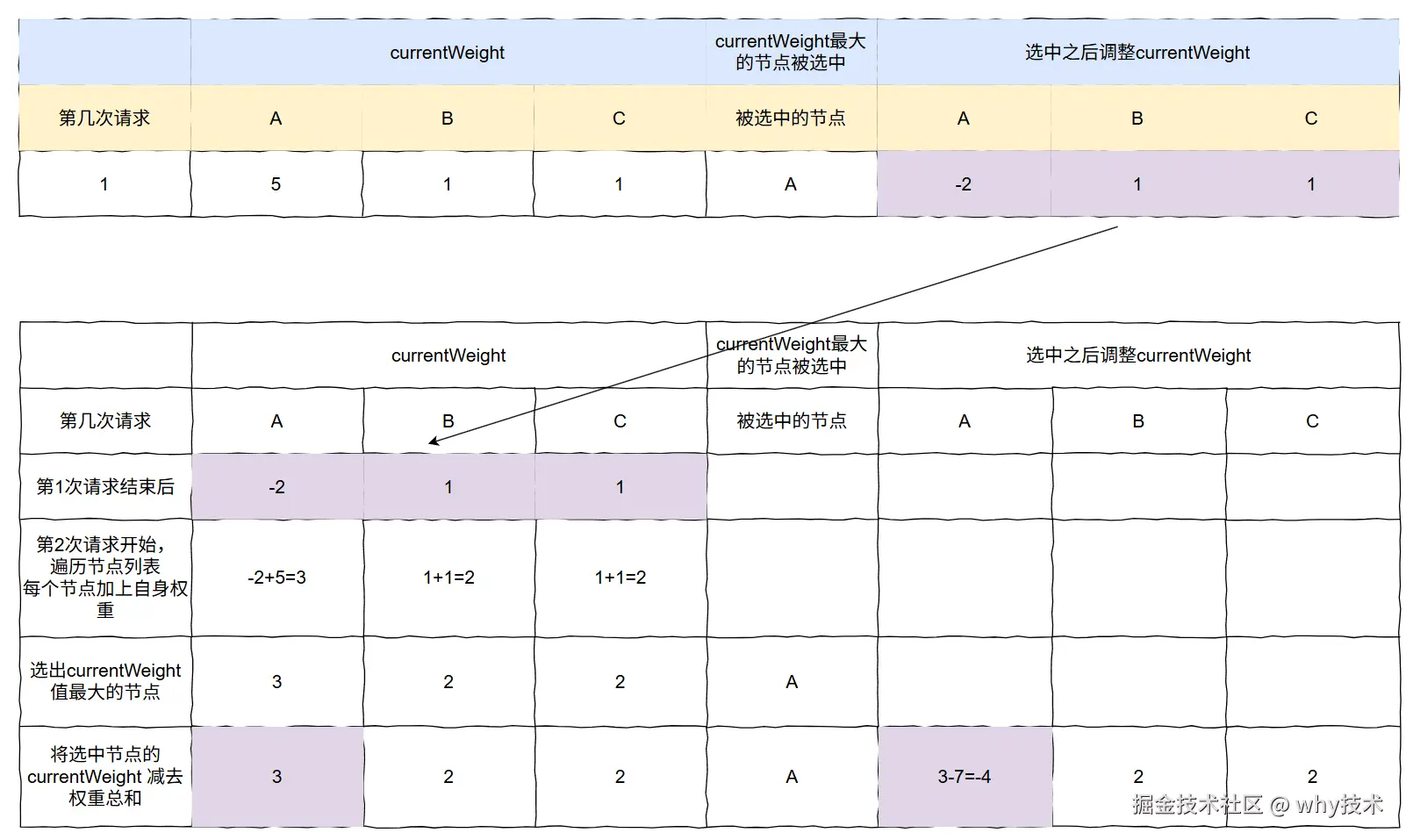
第一次请求结束后,调整之后的 currentWeight 是 A:B:C=-2:1:1。
现在第二次请求进来了,第一步会干啥?
遍历节点列表,让每个节点的 currentWeight 都加上自身权重。
所以:
- A 的 currentWeight=-2+5=3
- B 的 currentWeight=1+1=2
- C 的 currentWeight=1+1=2
还是 A 的 currentWeight 权重最高,第二次还是 A 来处理这个请求。
由于 A 被选中了,所以它的 currentWeight= 3-7=-4。
此时,每个节点的 currentWeight 为 A:B:C=-4:2:2。
按照上面的描述,我们再画个步骤图:
因此,第二次请求完成之后,整个结果图是这样的:
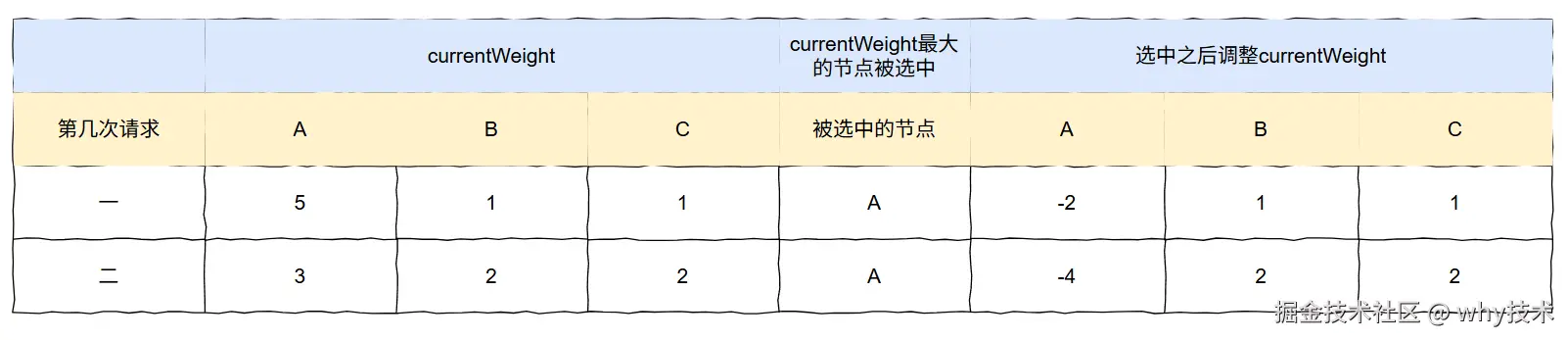
后面的内容哪怕你跳着看都行,但是在这一步, 你必须要明白第二次请求的这两组数字是怎么来的:
- A:B:C=3:2:2
- A:B:C=-4:2:2
第二次请求搞明白了,后面的请求就是依葫芦画瓢了。
第三次请求
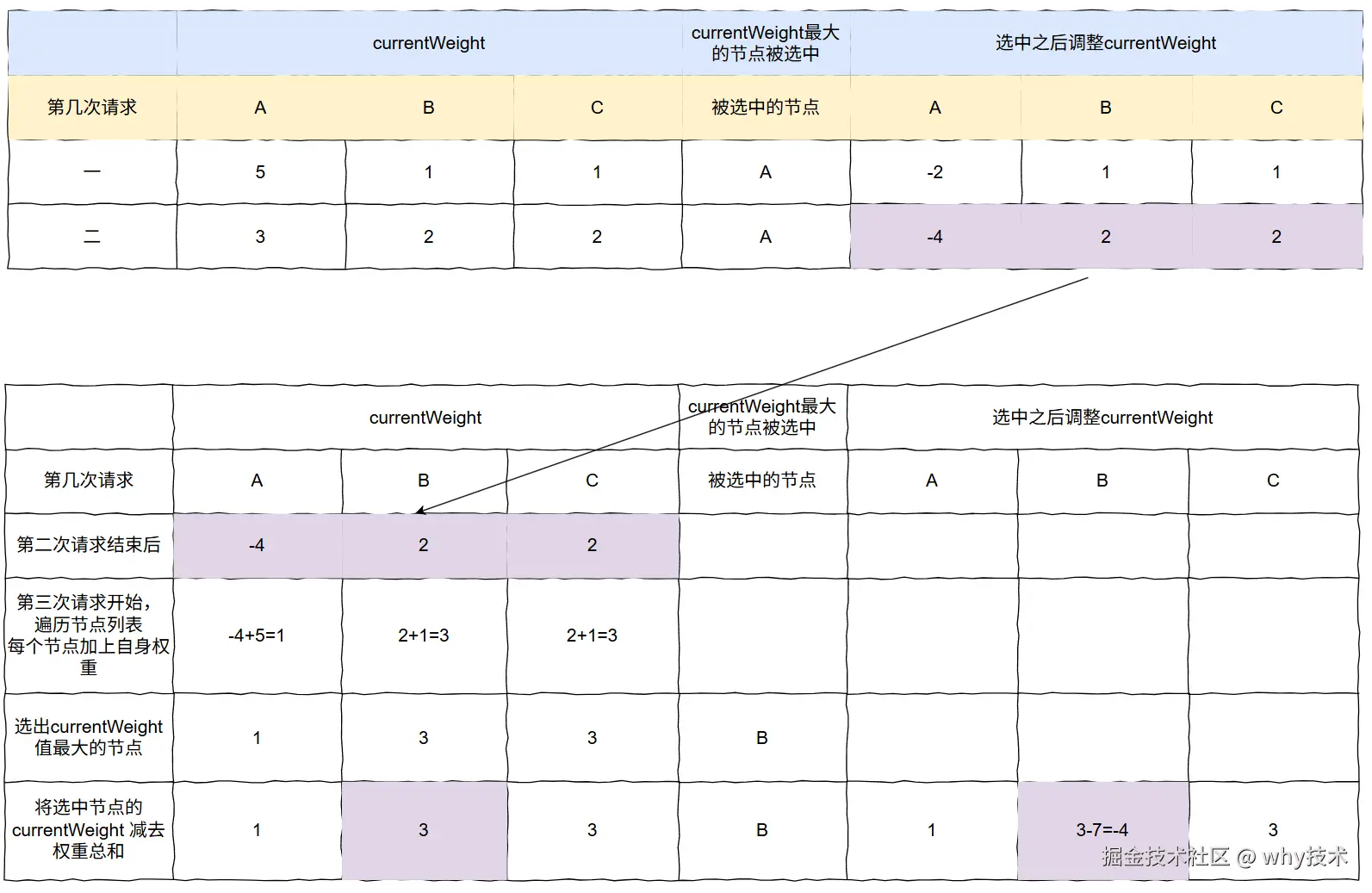
第二次请求结束后,调整之后的 currentWeight 是 A:B:C=-4:2:2。
现在第三次请求进来了,第一步会干啥?
老规矩:
遍历节点列表,让每个节点的 currentWeight 都加上自身权重。
所以:
- A 的 currentWeight=-4+5=1
- B 的 currentWeight=2+1=3
- C 的 currentWeight=2+1=3
这个时候,B、C 的权重都是 3,都最高,怎么办?
按照顺序来,就行。
选择 B。
由于 B 被选中了,所以它的 currentWeight= 3-7=-4。
此时,每个节点的 currentWeight 为 A:B:C=1:-4:3。
第三次请求,对应的步骤图是这样的:
对应的最终结果图是这样的:
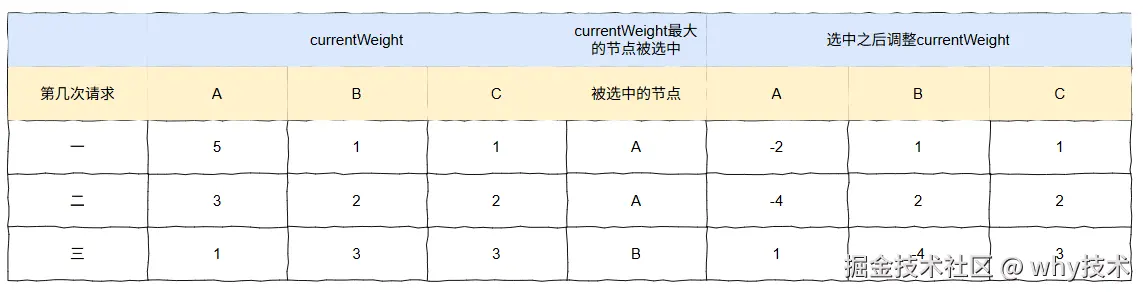
第四次请求
前面已经手摸手教学了三次了,后面的步骤就不详细描述了,直接上图了:
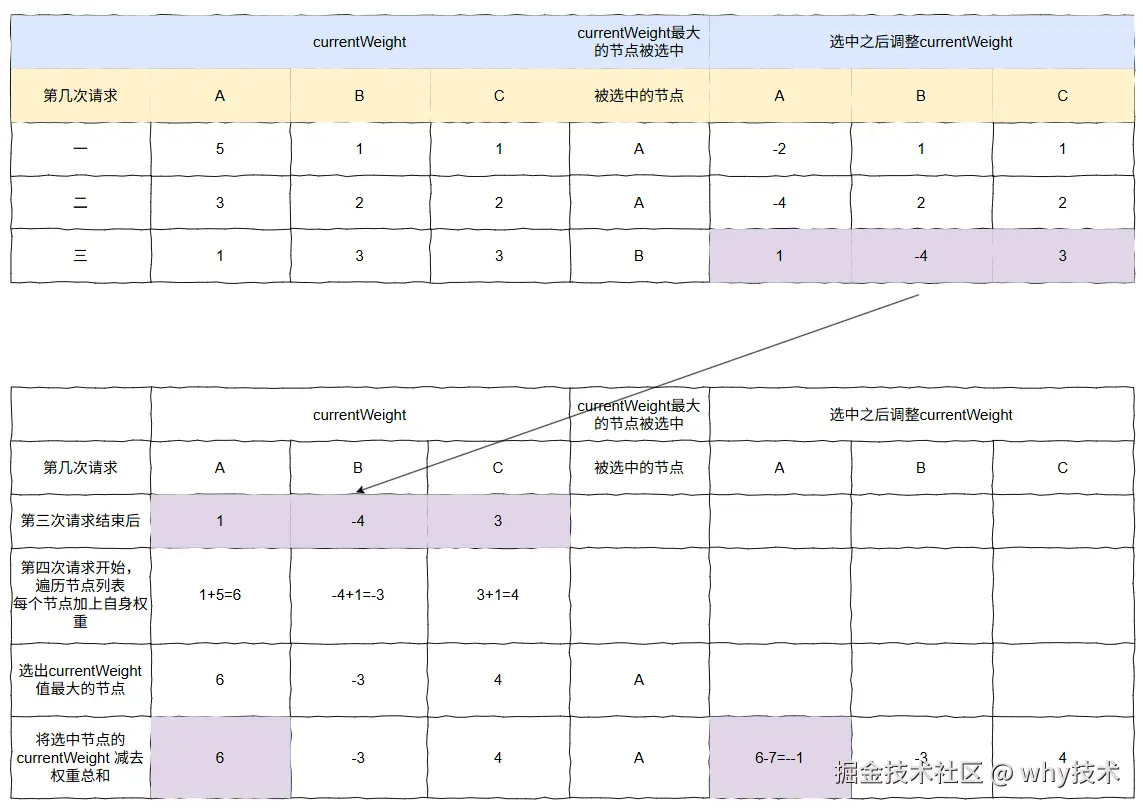
对应的最终结果图是这样的:
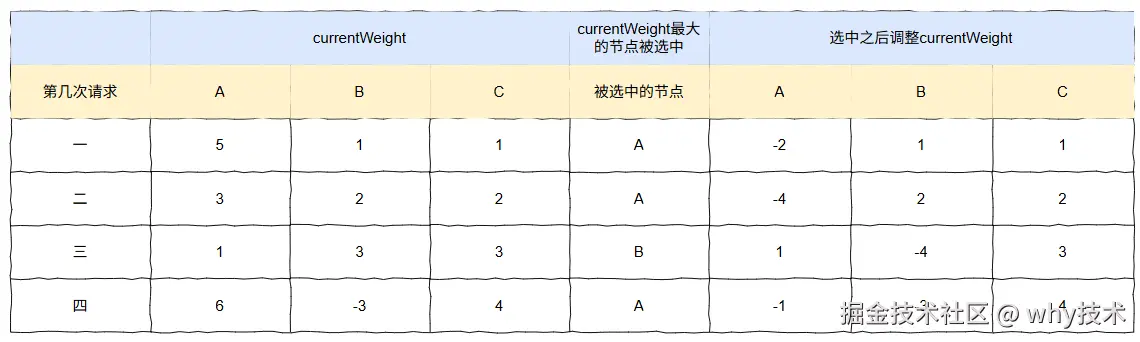
第五次请求
步骤图:
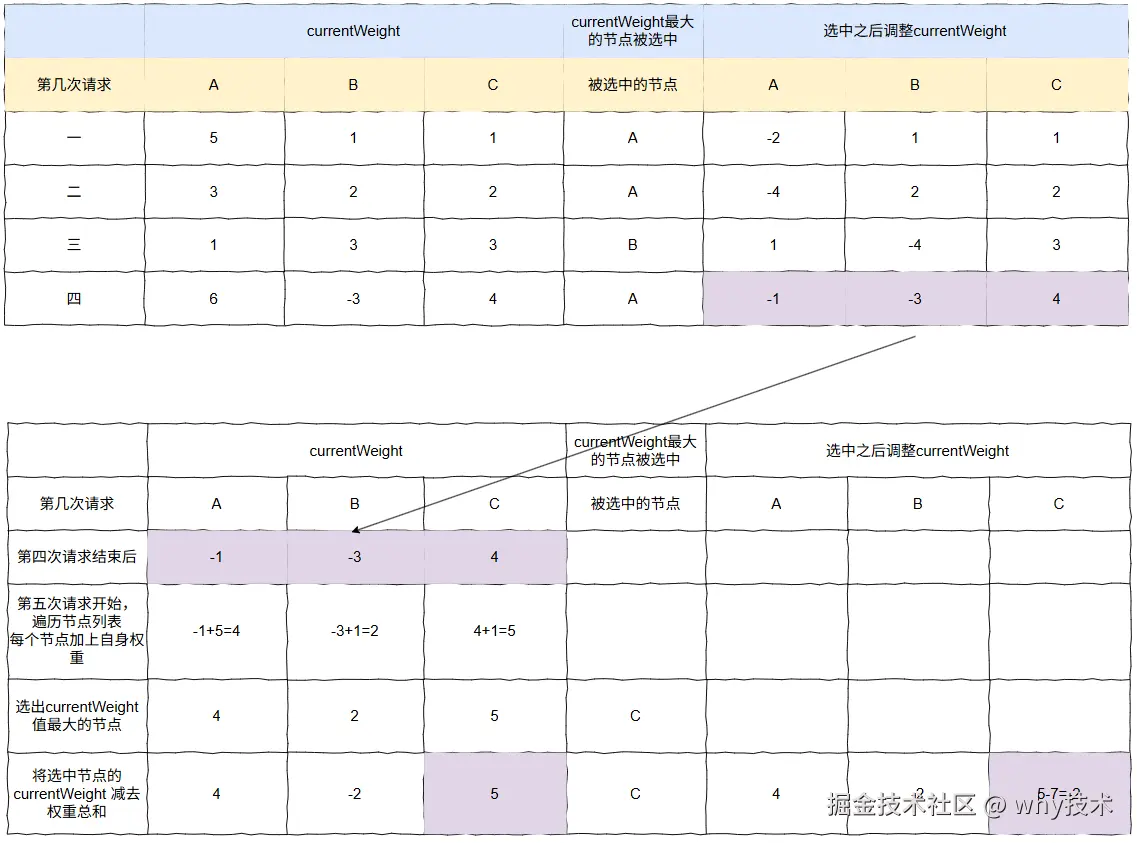
对应的最终结果图是这样的:
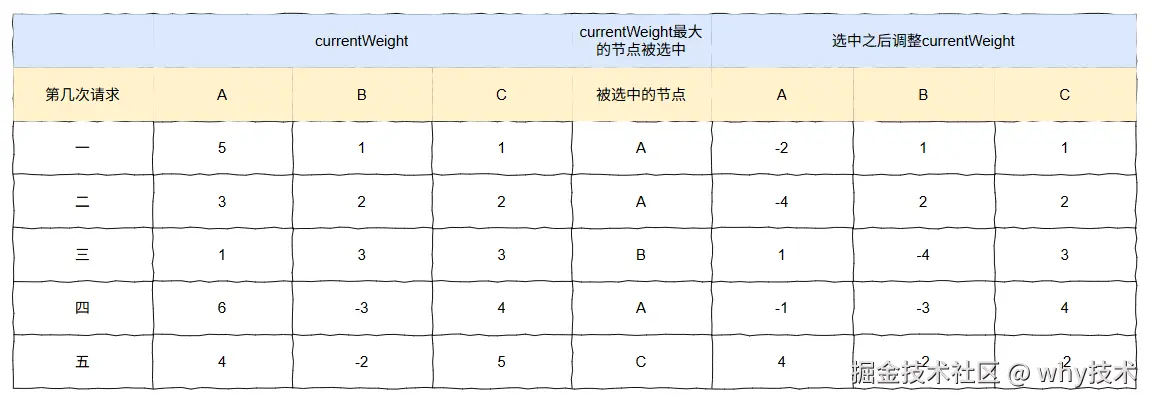
第六次请求
步骤图:
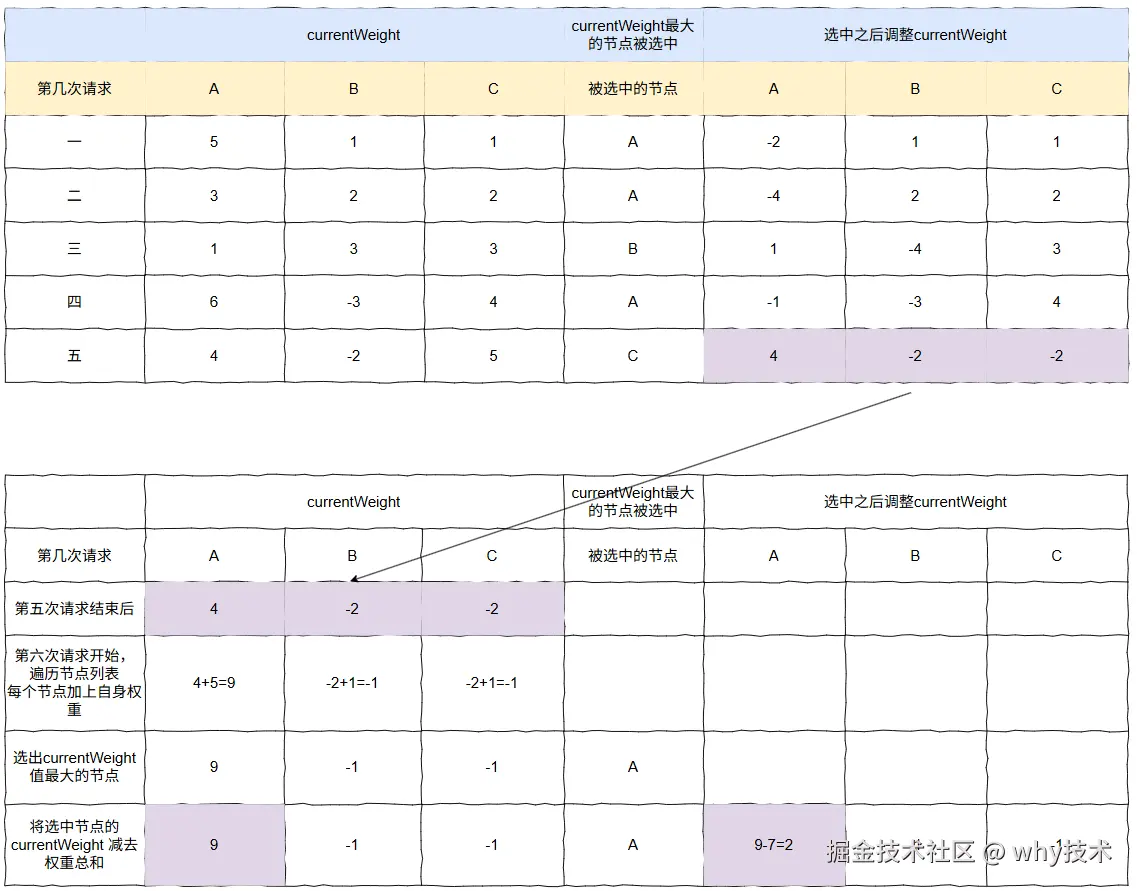
对应的最终结果图是这样的:
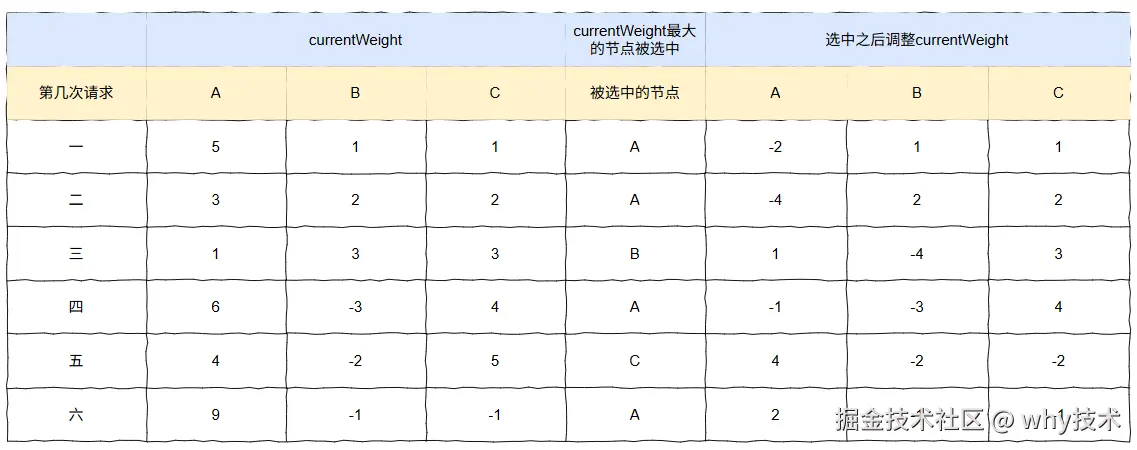
第七次请求
步骤图:
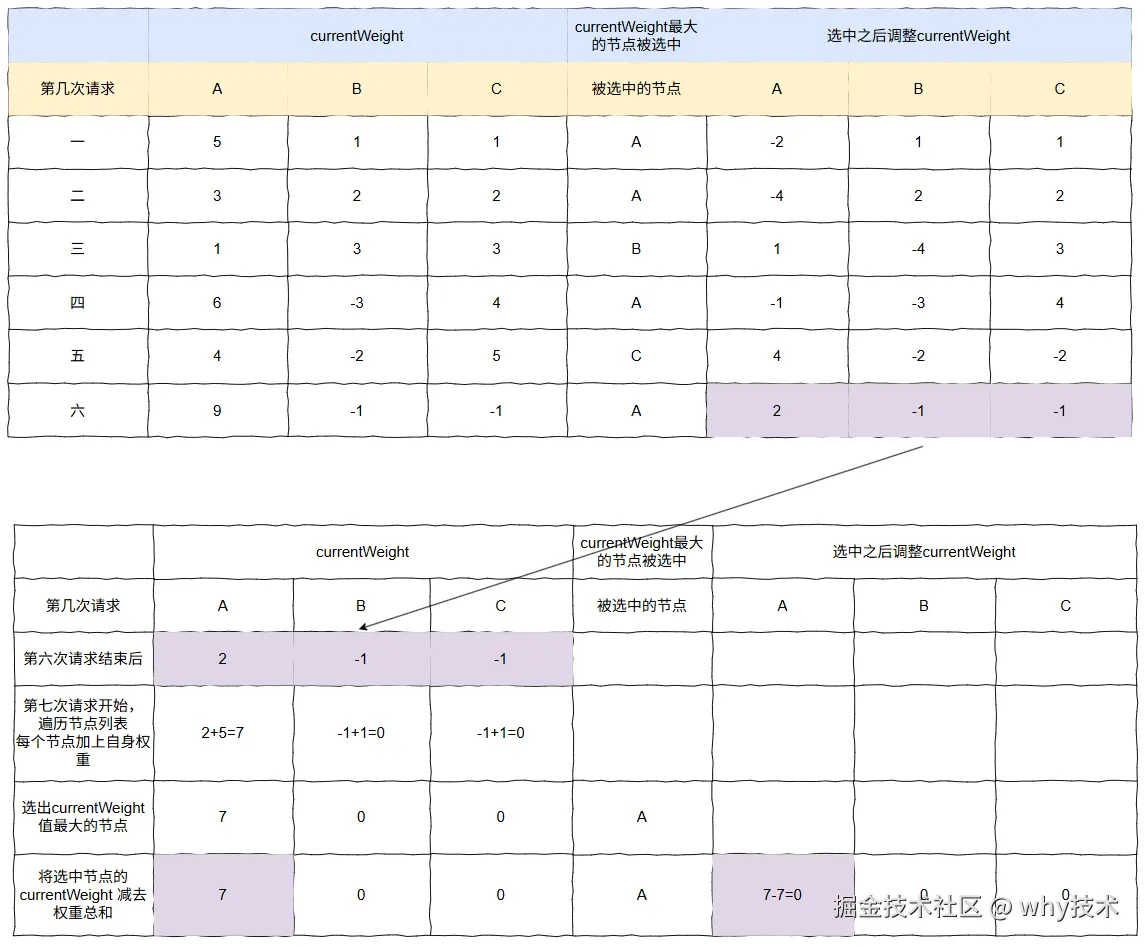
对应的最终结果图是这样的:
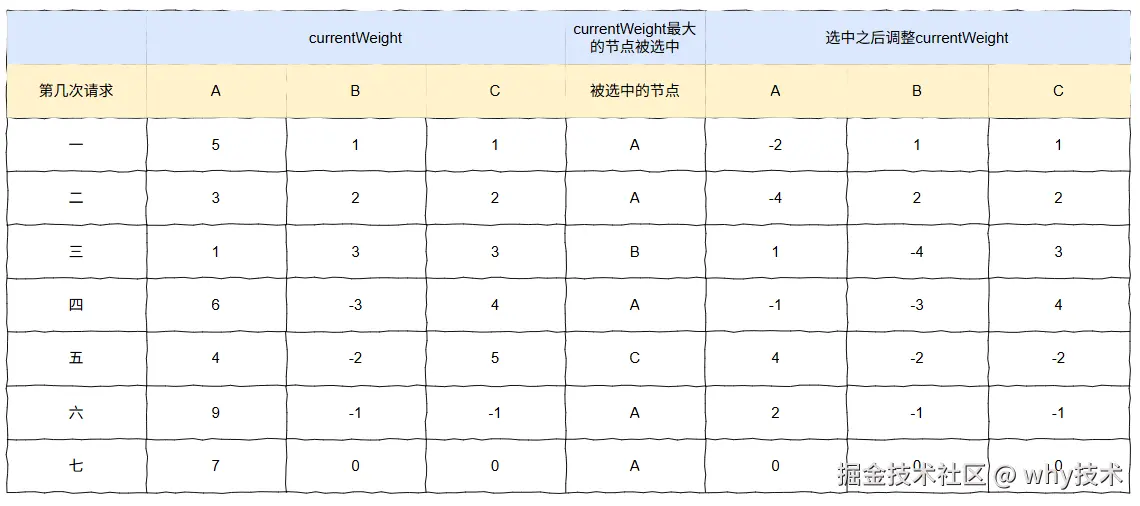
第八次请求
我知道你现在可能正在地铁上、公交上,也可能正在走路,在去上班的路上,或者是刚到公司正式开工之前准备摸一会鱼。
反正,不是一个沉浸式的学习场景,所以我画的这么多图,你可能是没有仔细看的,很快就滑到了这里。
没关系,不重要。
但是这第八步,很重要,是转折点,必须要认真看。
这是第八次的步骤图:
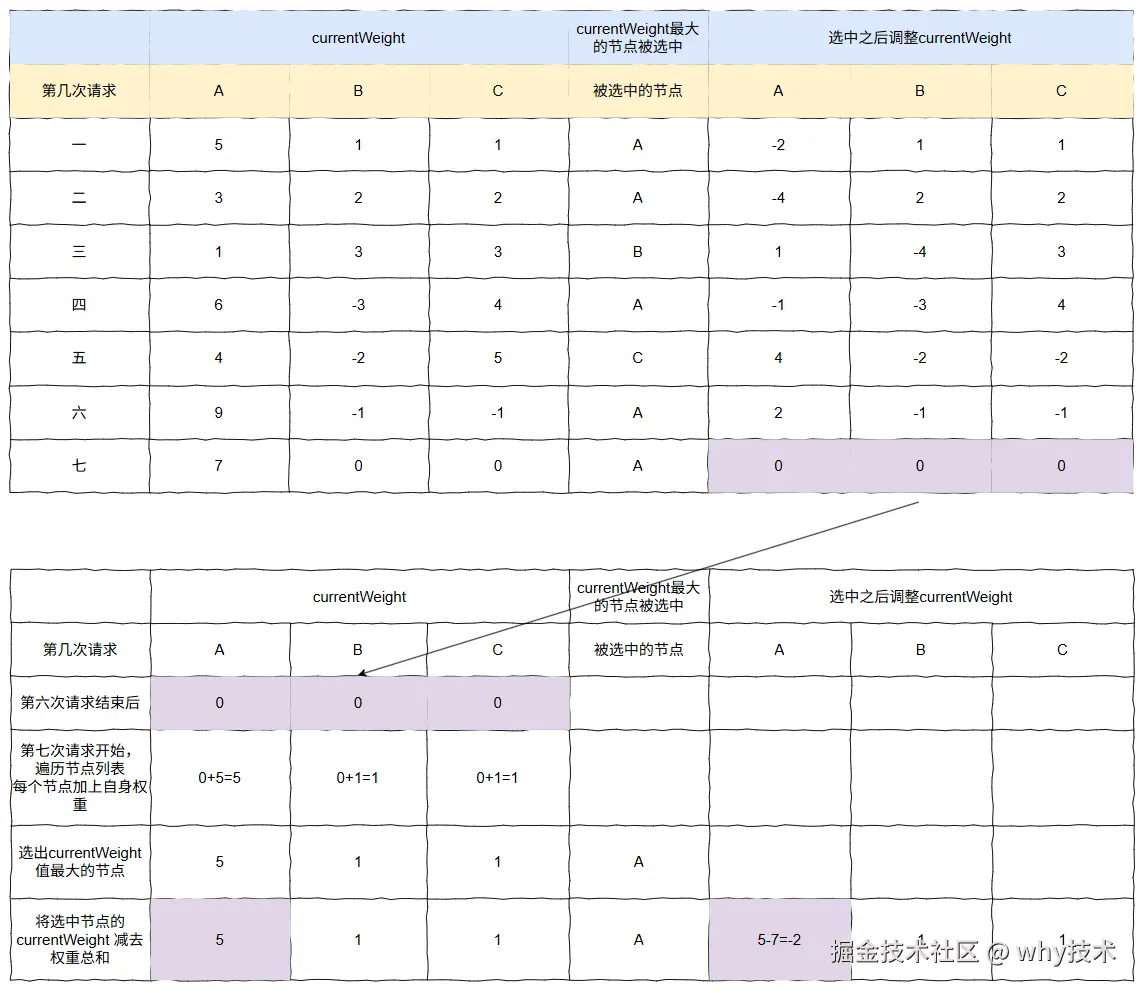
这是第八次请求完成后的最终的结果图:
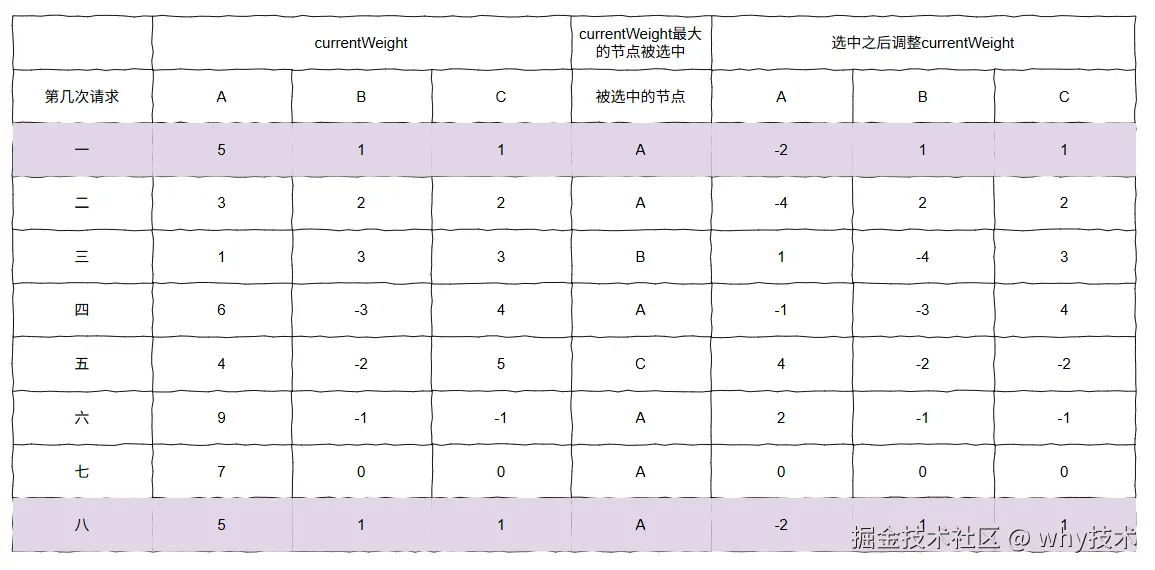
你看第八次请求之后的结果,和第一次请求之后的结果,一模一样。
这是什么,朋友?
这是闭环了呀,朋友。
前七次被选中的节点顺序为:
A->A->B->A->C->A->A
现在,闭环了,那后面的请求都会按照这个顺序去执行。
每七次请求,严格符合 A:B:C=5:1:1 的权重。
而且,不会出现连续把请求都发给 A 的情况。
对比一下就很明显了:
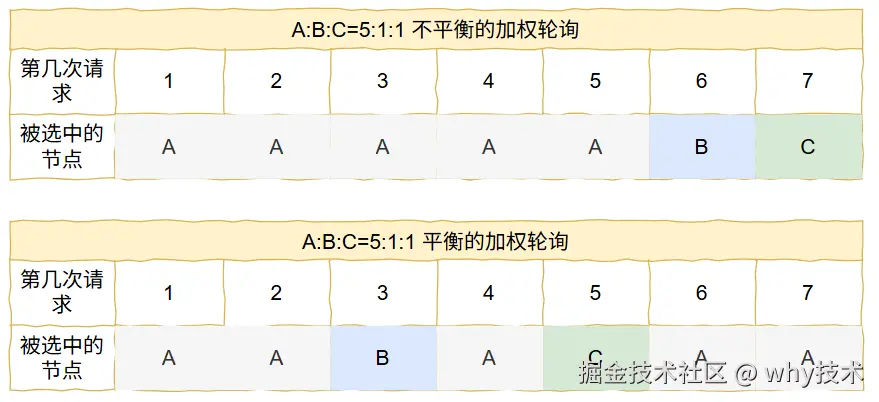
你说这个是不是显得平滑了很多。
功能确实实现了,但是...
关键就是这个但是。
但是,为什么?
经过上面的这一系列操作,它为什么就闭环了?
当年,我想了很久,我还是不知道背后的数学原理是什么。

反正就是隐隐约约觉得会闭环,但是你让我明明白白的描述出来为什么,我还真是说不出来。
我知道它能工作,但是不能证明它为什么能工作。所以,在我这个数学学渣面前,我觉得它是天才般的算法。
数学之美
现在,我要用数学的理论来证明,它确实是合理的。
这部分的内容,有一个非常重要的参考链接:
在这个链接里面,作者分别从"证明权重合理性"和"证明平滑性"这两个角度,论证了平滑加权轮询算法。
但是,有些步骤写的很简略,缺少进一步解释。且存在一些跳过简单步骤,直接用"不难得出"一笔带过的情况。
我又是一个数学不太好的娃儿,所以理解起来稍微有点费劲。
幸好有 DeepSeek 可以给我补充一下,我才算是理解了整个过程。
也是因此,才有了这篇文章。
下面的这部分,看起来非常非常"打脑壳",环境嘈杂、心神不定、心浮气躁的情况下,不建议看。看到数学符号就不舒服的,也不建议看。

证明权重合理性
首先,我们先证明权重合理性。
翻译过来就是要证明:在一轮循环过后,一个节点被选中的次数等于它的权重。
用数学的语言来表示就是:假设第 i 个节点,它的权重是 <math xmlns="http://www.w3.org/1998/Math/MathML"> x i x_i </math>xi,在一轮循环内,它最多被选中 <math xmlns="http://www.w3.org/1998/Math/MathML"> m i m_i </math>mi 次。
证明权重合理性就是要证明:
<math xmlns="http://www.w3.org/1998/Math/MathML"> x i = m i x_i=m_i </math>xi=mi
接下来我们开始证明。
假如有 n 个节点,记第 i 个节点的权重是 <math xmlns="http://www.w3.org/1998/Math/MathML"> x i x_i </math>xi。
设总权重为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> S = x 1 + x 2 + ... + x n S=x_1 + x_2 + ... + x_n </math>S=x1+x2+...+xn
前面介绍了,平滑加权的过程选择分两步:
- 第 1 步:遍历节点列表,让每个节点的 currentWeight 都加上自身权重。
- 第 2 步:将选中节点的 currentWeight 减去权重总和。
所以,n 个节点的初始化值为 [0, 0, ..., 0],数组长度为 n,值都为 0。
第一轮选择的第 1 步执行后,数组的值为 [ <math xmlns="http://www.w3.org/1998/Math/MathML"> x 1 x_1 </math>x1, <math xmlns="http://www.w3.org/1998/Math/MathML"> x 2 x_2 </math>x2, ..., <math xmlns="http://www.w3.org/1998/Math/MathML"> x n x_n </math>xn]。
假设第 1 步后,最大的节点为 j,则第 2 步就是 节点 j 减去 S。
所以第 2 步之后的数组为 [ <math xmlns="http://www.w3.org/1998/Math/MathML"> x 1 x_1 </math>x1, <math xmlns="http://www.w3.org/1998/Math/MathML"> x 2 x_2 </math>x2, ..., <math xmlns="http://www.w3.org/1998/Math/MathML"> x j x_j </math>xj-S, ..., <math xmlns="http://www.w3.org/1998/Math/MathML"> x n x_n </math>xn]。
执行完第 2 步后,数组的和为: <math xmlns="http://www.w3.org/1998/Math/MathML"> x 1 + x 2 + ... + x j − S + ... + x n x_1 + x_2 + ... + x_j-S + ... + x_n </math>x1+x2+...+xj−S+...+xn
把上面的 "-S" 移到最后: <math xmlns="http://www.w3.org/1998/Math/MathML"> x 1 + x 2 + ... + x j + ... + x n − S x_1 + x_2 + ... + x_j + ... + x_n-S </math>x1+x2+...+xj+...+xn−S
而前面我们说了: <math xmlns="http://www.w3.org/1998/Math/MathML"> S = x 1 + x 2 + ... + x n S=x_1 + x_2 + ... + x_n </math>S=x1+x2+...+xn
所以:
<math xmlns="http://www.w3.org/1998/Math/MathML"> x 1 + x 2 + ... + x j − S + ... + x n = x_1 + x_2 + ... + x_j-S + ... + x_n = </math>x1+x2+...+xj−S+...+xn= <math xmlns="http://www.w3.org/1998/Math/MathML"> x 1 + x 2 + ... + x j + ... + x n − S = x_1 + x_2 + ... + x_j + ... + x_n - S = </math>x1+x2+...+xj+...+xn−S= <math xmlns="http://www.w3.org/1998/Math/MathML"> = S − S =S - S </math>=S−S <math xmlns="http://www.w3.org/1998/Math/MathML"> = 0 = 0 </math>=0
由此可得,每轮选择完后的数组总和都为 0。
这一点,我们从前面的图片中也能得到证实。
你看我标准了颜色的部分,每次选择完成后,三个数字之和恒等于 0:
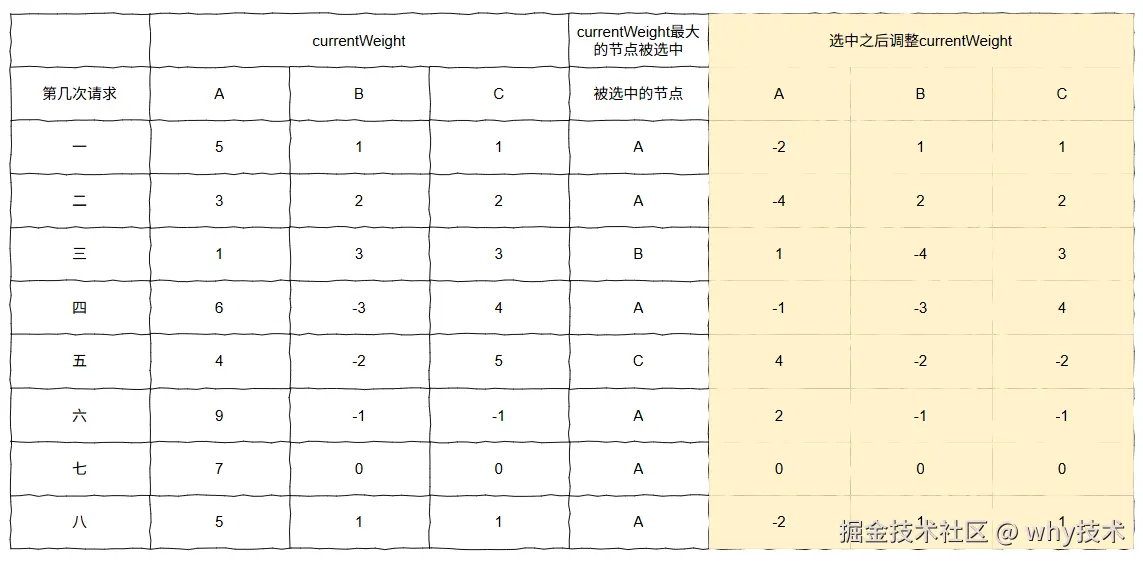
假设总共执行 S 轮选择,记第 i 个节点选择了 <math xmlns="http://www.w3.org/1998/Math/MathML"> m i m_i </math>mi 次,第 i 个节点的当前权重(currentWeight)为 <math xmlns="http://www.w3.org/1998/Math/MathML"> w i w_i </math>wi。
假设节点 j 在第 t 轮 (t < S) 之前,已经被选择了 <math xmlns="http://www.w3.org/1998/Math/MathML"> x j x_j </math>xj 次(即节点 j 权重的次数),记此时第 j 个节点的当前权重为 <math xmlns="http://www.w3.org/1998/Math/MathML"> w j w_j </math>wj。
不难得出:
<math xmlns="http://www.w3.org/1998/Math/MathML"> w j = t ∗ x j − x j ∗ S w_j = t * x_j - x_j * S </math>wj=t∗xj−xj∗S
等等...
上面这个"不难得出"的公式,是怎么来的?

我给你盘一下。
每一轮不管节点 j 是否被选中,都会加上它自己的权重,即 <math xmlns="http://www.w3.org/1998/Math/MathML"> x j x_j </math>xj。
那么 t 轮之后,它的权重总共加了 <math xmlns="http://www.w3.org/1998/Math/MathML"> t ∗ x j t * x_j </math>t∗xj 这么多。
而在我们的假设中:节点 j 在第 t 轮 (t < S) 之前,已经被选择了 <math xmlns="http://www.w3.org/1998/Math/MathML"> x j x_j </math>xj 次。
每次被选中,会减去总权重 S,那就是 <math xmlns="http://www.w3.org/1998/Math/MathML"> x j ∗ S x_j * S </math>xj∗S。
所以,第 j 个节点的当前权重为
<math xmlns="http://www.w3.org/1998/Math/MathML"> w j = t ∗ x j − x j ∗ S w_j = t * x_j - x_j * S </math>wj=t∗xj−xj∗S
即:
<math xmlns="http://www.w3.org/1998/Math/MathML"> w j = ( t − S ) ∗ x j w_j = (t - S) * x_j </math>wj=(t−S)∗xj
又因为 t 恒小于 S,所以 t - S < 0。
又因为 <math xmlns="http://www.w3.org/1998/Math/MathML"> x j x_j </math>xj 是大于 0(权重为正数),所以, <math xmlns="http://www.w3.org/1998/Math/MathML"> w j < 0 w_j < 0 </math>wj<0。
前面假设了总共执行 S 轮选择,t 轮之后,则剩下 S-t 轮。
前面已经证得:
<math xmlns="http://www.w3.org/1998/Math/MathML"> w j < 0 w_j < 0 </math>wj<0
那么在剩余的 S-t 轮中,每轮节点 j 都会增加其权重 <math xmlns="http://www.w3.org/1998/Math/MathML"> x j x_j </math>xj(第一步操作)。
因此,在剩余的轮次中,节点 j 的权重将增加 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( S − t ) ∗ x j (S - t) * x_j </math>(S−t)∗xj
在 S 轮全部结束后,节点 j 的权重为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> ( t − S ) ∗ x j + ( S − t ) ∗ x j = 0 (t - S) * x_j + (S - t) * x_j = 0 </math>(t−S)∗xj+(S−t)∗xj=0
由于节点 j 可以是任何一个节点,即 S 轮结束后,每个节点的权重都为 0。
这也符合前面我们证得的:每轮后权重总和为 0 的性质。
同时,从前面的图片中也能得到呼应:
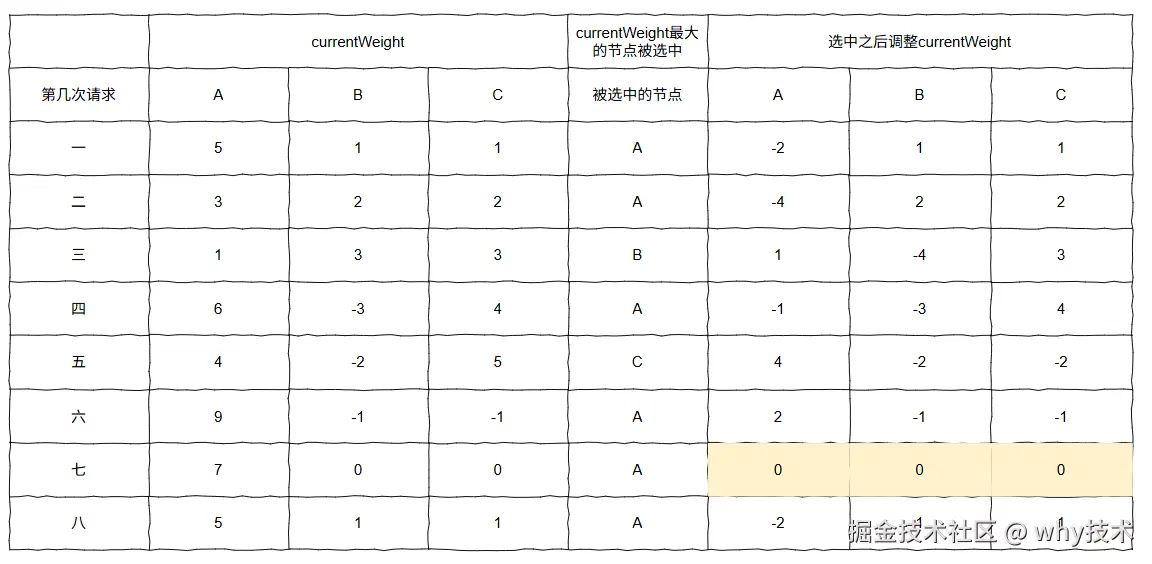
现在,我们回到这里:
前面假设了总共执行 S 轮选择,t 轮之后,则剩下 S-t 轮。
由于我们前面证得了 S 轮结束后,节点 j 的权重为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> ( t − S ) ∗ x j + ( S − t ) ∗ x j = 0 (t - S) * x_j + (S - t) * x_j = 0 </math>(t−S)∗xj+(S−t)∗xj=0
所以在剩下的 S-t 选择中,wj 的值从 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( t − S ) ∗ x j < 0 (t - S) * x_j < 0 </math>(t−S)∗xj<0 开始,每轮增加 <math xmlns="http://www.w3.org/1998/Math/MathML"> x j x_j </math>xj,逐渐趋近于 0,但直到最后一轮才达到 0。
因此,在剩余轮次中的任何时刻,节点 j 的权重 <math xmlns="http://www.w3.org/1998/Math/MathML"> w j w_j </math>wj 都小于或等于 0(只有在最后一轮结束时才等于 0)。
又因为,前面已经证明的"任何一轮选择后,数组总和都为 0"这个结论。
所以,在剩余轮次中的任何时刻,由于节点 j 的权重 <math xmlns="http://www.w3.org/1998/Math/MathML"> w j w_j </math>wj 都小于或等于 0,则必定存在一个节点 k 使得 <math xmlns="http://www.w3.org/1998/Math/MathML"> w k > 0 w_k > 0 </math>wk>0。
因此,剩余轮次中永远不会再选中 j 节点。
这一点,在图片中同样可以验证:
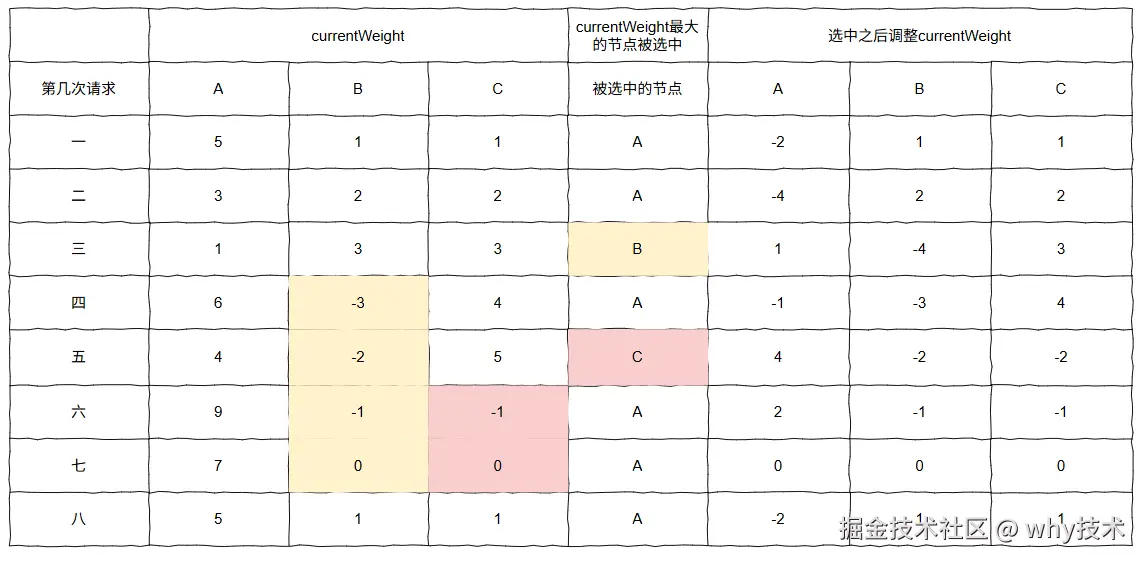
B、C 节点,在被选中之后,在剩余轮次中的任何时刻,权重都小于 0,只有在最后一轮(即第七次请求)结束时才等于 0。且它们在剩余轮次中都不会被选中了。
好,回到我们的证明中。
因为我们前面假设的是:
- 假设总共执行 S 轮选择,记第 i 个节点选择了 <math xmlns="http://www.w3.org/1998/Math/MathML"> m i m_i </math>mi 次。
- 又假设节点 j 在第 t 轮 (t < S) 之前,已经被选择了 <math xmlns="http://www.w3.org/1998/Math/MathML"> x j x_j </math>xj 次(即节点 j 权重的次数)。
综上,可以得出,第 i 个节点最多被选中 xi 次,即:
<math xmlns="http://www.w3.org/1998/Math/MathML"> m i < = x i m_i <= x_i </math>mi<=xi
<math xmlns="http://www.w3.org/1998/Math/MathML"> m i m_i </math>mi 是选中的次数, <math xmlns="http://www.w3.org/1998/Math/MathML"> x i x_i </math>xi 是 i 节点的权重。
因为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> S = m 1 + m 2 + ... + m n S = m1 + m2 + ... + mn </math>S=m1+m2+...+mn <math xmlns="http://www.w3.org/1998/Math/MathML"> S = x 1 + x 2 + ... + x n S = x1 + x2 + ... + xn </math>S=x1+x2+...+xn
所以,可以得出 <math xmlns="http://www.w3.org/1998/Math/MathML"> m i = x i m_i=x_i </math>mi=xi,它和 <math xmlns="http://www.w3.org/1998/Math/MathML"> m i < = x i m_i <= x_i </math>mi<=xi 并不冲突。
但是还记得我们要证明的是什么吗?
用数学的语言来表示就是:假设第 i 个节点,它的权重是 <math xmlns="http://www.w3.org/1998/Math/MathML"> x i x_i </math>xi,在一轮循环内,它最多被选中 <math xmlns="http://www.w3.org/1998/Math/MathML"> m i m_i </math>mi 次。
证明权重合理性就是要证明:
<math xmlns="http://www.w3.org/1998/Math/MathML"> x i = m i x_i=m_i </math>xi=mi
现在我们证明了 <math xmlns="http://www.w3.org/1998/Math/MathML"> m i < = x i m_i <= x_i </math>mi<=xi,还多出了 <math xmlns="http://www.w3.org/1998/Math/MathML"> m i < x i m_i < x_i </math>mi<xi 这部分。
这里来个反证法。
如果任何一个 <math xmlns="http://www.w3.org/1998/Math/MathML"> m i m_i </math>mi 小于 <math xmlns="http://www.w3.org/1998/Math/MathML"> x i x_i </math>xi,则至少有一个其他的节点 k,对应的 <math xmlns="http://www.w3.org/1998/Math/MathML"> m k m_k </math>mk 必须大于 <math xmlns="http://www.w3.org/1998/Math/MathML"> x k x_k </math>xk,才能保持下面这个公式相等:
<math xmlns="http://www.w3.org/1998/Math/MathML"> S = m 1 + m 2 + ... + m n S = m1 + m2 + ... + mn </math>S=m1+m2+...+mn <math xmlns="http://www.w3.org/1998/Math/MathML"> S = x 1 + x 2 + ... + x n S = x1 + x2 + ... + xn </math>S=x1+x2+...+xn
但我们已经证得了 <math xmlns="http://www.w3.org/1998/Math/MathML"> m i < = x i m_i <= x_i </math>mi<=xi, <math xmlns="http://www.w3.org/1998/Math/MathML"> m k > x k m_k > x_k </math>mk>xk 与之矛盾。
因此,唯一的可能性就是,对于所有的节点 i 来说:
<math xmlns="http://www.w3.org/1998/Math/MathML"> x i = m i x_i=m_i </math>xi=mi
权重合理性,证明完毕!

证明平滑性
接下来证明平滑性。
要证明平滑性,只要证明不是一直连续选择同一个节点即可。
跟上面一样,假设总权重为 S,假如某个节点 i 连续选择了 <math xmlns="http://www.w3.org/1998/Math/MathML"> t ( t < x i ) t(t < x_i) </math>t(t<xi) 次,只要存在下一次选择的不是 i ,即可证明是平滑的。
假设 <math xmlns="http://www.w3.org/1998/Math/MathML"> t = x i − 1 t = x_i - 1 </math>t=xi−1,即它还差一次就到了最大被选中次数了。
此是第 i 个节点的当前权重为 <math xmlns="http://www.w3.org/1998/Math/MathML"> w i w_i </math>wi。
不难得出:
<math xmlns="http://www.w3.org/1998/Math/MathML"> w i = t ∗ x i − t ∗ S w_i= t * x_i - t * S </math>wi=t∗xi−t∗S
这个不难得出就不展开讲了,前面证明权重合理性的时候已经"不难得出"过了。
代入:
<math xmlns="http://www.w3.org/1998/Math/MathML"> t = x i − 1 t = x_i - 1 </math>t=xi−1
即:
<math xmlns="http://www.w3.org/1998/Math/MathML"> w i = t ∗ x i − t ∗ S = w_i=t * x_i - t * S = </math>wi=t∗xi−t∗S= <math xmlns="http://www.w3.org/1998/Math/MathML"> ( x i − 1 ) ∗ x i − ( x i − 1 ) ∗ S (x_i - 1) * x_i - (x_i - 1) * S </math>(xi−1)∗xi−(xi−1)∗S
前面介绍了,平滑加权的过程选择分两步:
- 第 1 步:遍历节点列表,让每个节点的 currentWeight 都加上自身权重。
- 第 2 步:将选中节点的 currentWeight 减去权重总和。
接下来,证明下一轮的第 1 步执行完的值 <math xmlns="http://www.w3.org/1998/Math/MathML"> w i + x i w_i+x_i </math>wi+xi 不是最大的即可。
代入前面算出的 <math xmlns="http://www.w3.org/1998/Math/MathML"> w i w_i </math>wi:
<math xmlns="http://www.w3.org/1998/Math/MathML"> w i + x i = w_i+x_i= </math>wi+xi= <math xmlns="http://www.w3.org/1998/Math/MathML"> ( x i − 1 ) ∗ x i − ( x i − 1 ) ∗ S + x i = (x_i - 1) * x_i - (x_i - 1) * S+ x_i= </math>(xi−1)∗xi−(xi−1)∗S+xi= <math xmlns="http://www.w3.org/1998/Math/MathML"> x i 2 − x i ∗ S + S = x_i²-x_i*S+S= </math>xi2−xi∗S+S= <math xmlns="http://www.w3.org/1998/Math/MathML"> ( x i − 1 ) ∗ ( x i − S ) + x i (x_i-1)*(x_i-S)+x_i </math>(xi−1)∗(xi−S)+xi
因为 <math xmlns="http://www.w3.org/1998/Math/MathML"> x i x_i </math>xi 恒小于 S,除去 i 节点外,其他节点的权重之和至少为 1 ,所以:
<math xmlns="http://www.w3.org/1998/Math/MathML"> x i − S < = − 1 x_i-S<=-1 </math>xi−S<=−1
代入上面:
<math xmlns="http://www.w3.org/1998/Math/MathML"> ( x i − 1 ) ∗ ( x i − S ) + x i < = (x_i-1)*(x_i-S)+x_i<= </math>(xi−1)∗(xi−S)+xi<= <math xmlns="http://www.w3.org/1998/Math/MathML"> ( x i − 1 ) ∗ − 1 + x i = (x_i-1)*-1+x_i= </math>(xi−1)∗−1+xi= <math xmlns="http://www.w3.org/1998/Math/MathML"> − x i + 1 + x i = 1 -x_i+1+x_i=1 </math>−xi+1+xi=1
所以,第 t 轮后,对于 i 节点,在执行完第 1 步后的当前权重值为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> w i + x i < = 1 w_i + x_i <= 1 </math>wi+xi<=1
如果这 t 轮刚好是最开始的 t 轮,即,从第 1 轮到第 t 轮,节点 i 都被选中。
此时,必定存在另一个节点 j 的当前权重值为 <math xmlns="http://www.w3.org/1998/Math/MathML"> x j ∗ t x_j*t </math>xj∗t
节点 j 在执行完第 1 步后的当前权重值就变成了:
<math xmlns="http://www.w3.org/1998/Math/MathML"> x j ∗ t + x j = x j ( t + 1 ) x_j*t+x_j=x_j(t+1) </math>xj∗t+xj=xj(t+1)
由于:
<math xmlns="http://www.w3.org/1998/Math/MathML"> x j > = 1 , t > = 1 x_j>=1,t>=1 </math>xj>=1,t>=1
所以:
<math xmlns="http://www.w3.org/1998/Math/MathML"> x j ( t + 1 ) > = 1 ∗ ( 1 + 1 ) = 2 x_j(t+1)>=1*(1+1)=2 </math>xj(t+1)>=1∗(1+1)=2
因此,节点 j 的权重,至少为 2,而节点 i 的权重至多为 1。
所以,节点 j 的权重大于节点 i 的权重,节点 i 不会被选中。
这就证明了平滑性。

One More Thing
前面我提到了一个链接:
这个链接,你直接打开的话是这样的:
不知道为什么被作者删除了。
但是为什么我还能参考呢?
这就得说到很久以前,我在网上吃瓜的时候,捡到的一个宝藏网站。

首先,访问这个网站需要你掌握较为正确的上网的姿势:
这个网站是"互联网档案馆"(Internet Archive),1996 年成立的非营利组织维护的网站。
目的是建立一个数字化的全球互联网图书馆,以保留互联网上的文化遗产,使其能够被后代访问和研究。
收藏了的内容有免费书籍、电影、软件、音乐、网站等。

前面的 946B 的 B 我还专门查了一下这是个什么计数单位。
1B=10亿,946B 就是 9460 亿个网站。
那么这个网页可以干什么呢?
我给你展示一个。
比如,我想看看淘宝网的首页变迁历史。
那么我可以把淘宝的域名放在这里,进行搜索:

搜索结果是这样的:
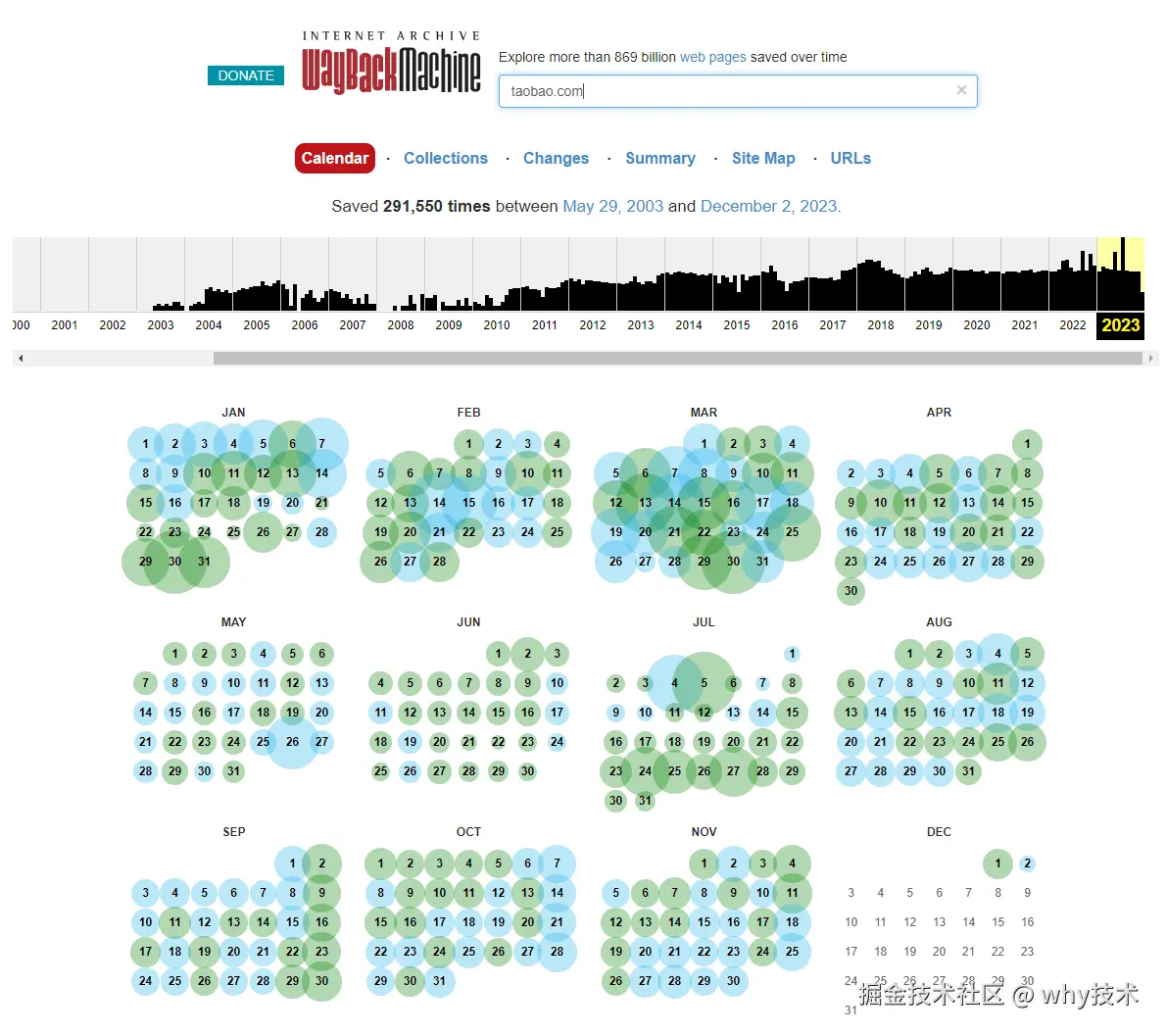
颜色越深代表快照越多:
从上面的时间轴来看,从 2003 年这个网站上就有淘宝首页的快照了,截至到现在有 29w 个快照,跨越了 20 年。
第一个快照是 2003 年 6 月 12 日,彼时的淘宝正式上线运营了 1 个月的时间,一眼望去,这厚重的历史感:
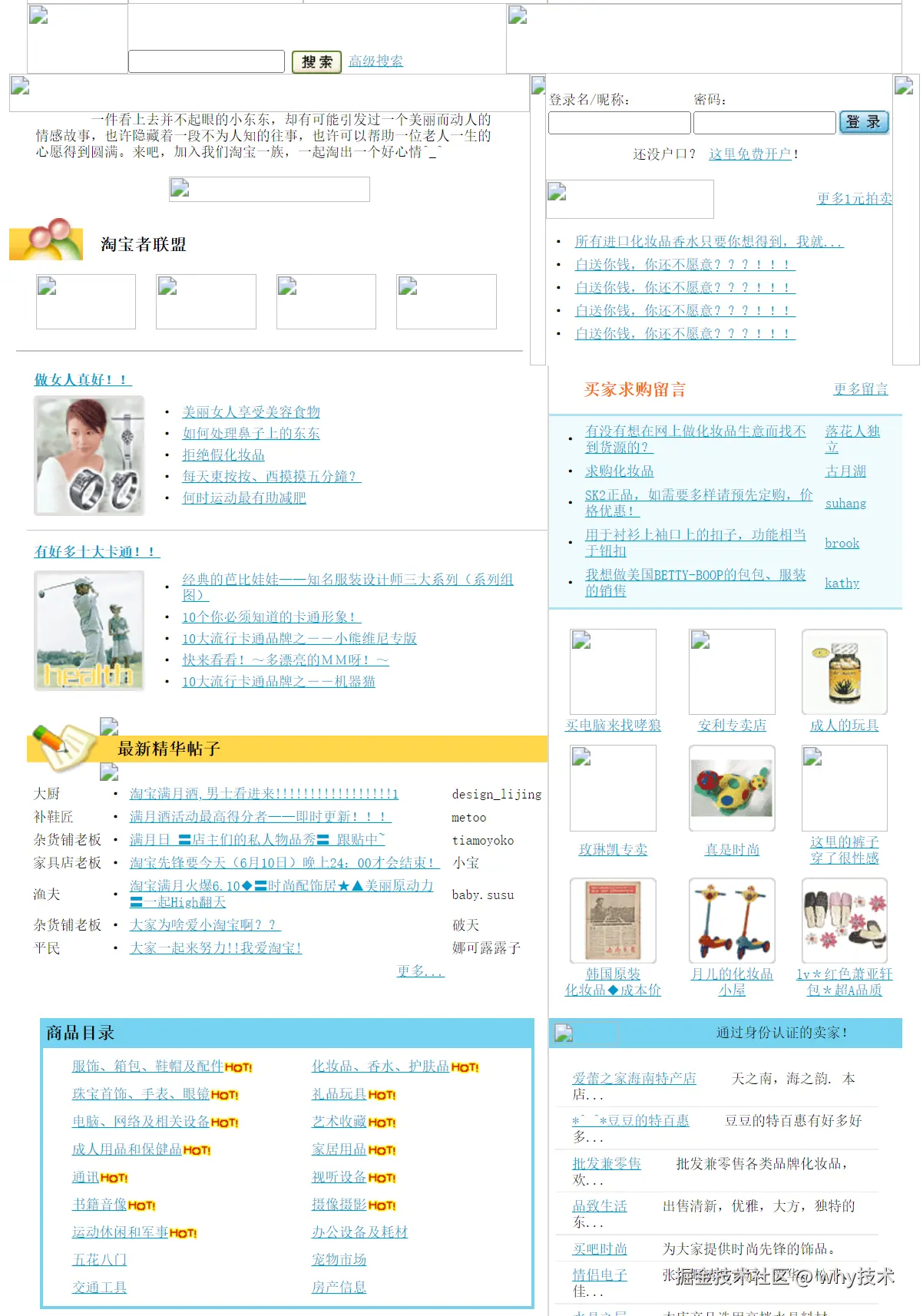
这是 2005 年 11 月 1 日的淘宝:
这是 2008 年 12 月 23 日的淘宝:
越往后翻,越眼熟,越不像是"擦边小网站",这些都是淘宝成长的痕迹。
所以,同理,我试着把前面提到的链接放到这里去搜索一下。
就能看到从 2021 年就开始采集到这个网站。
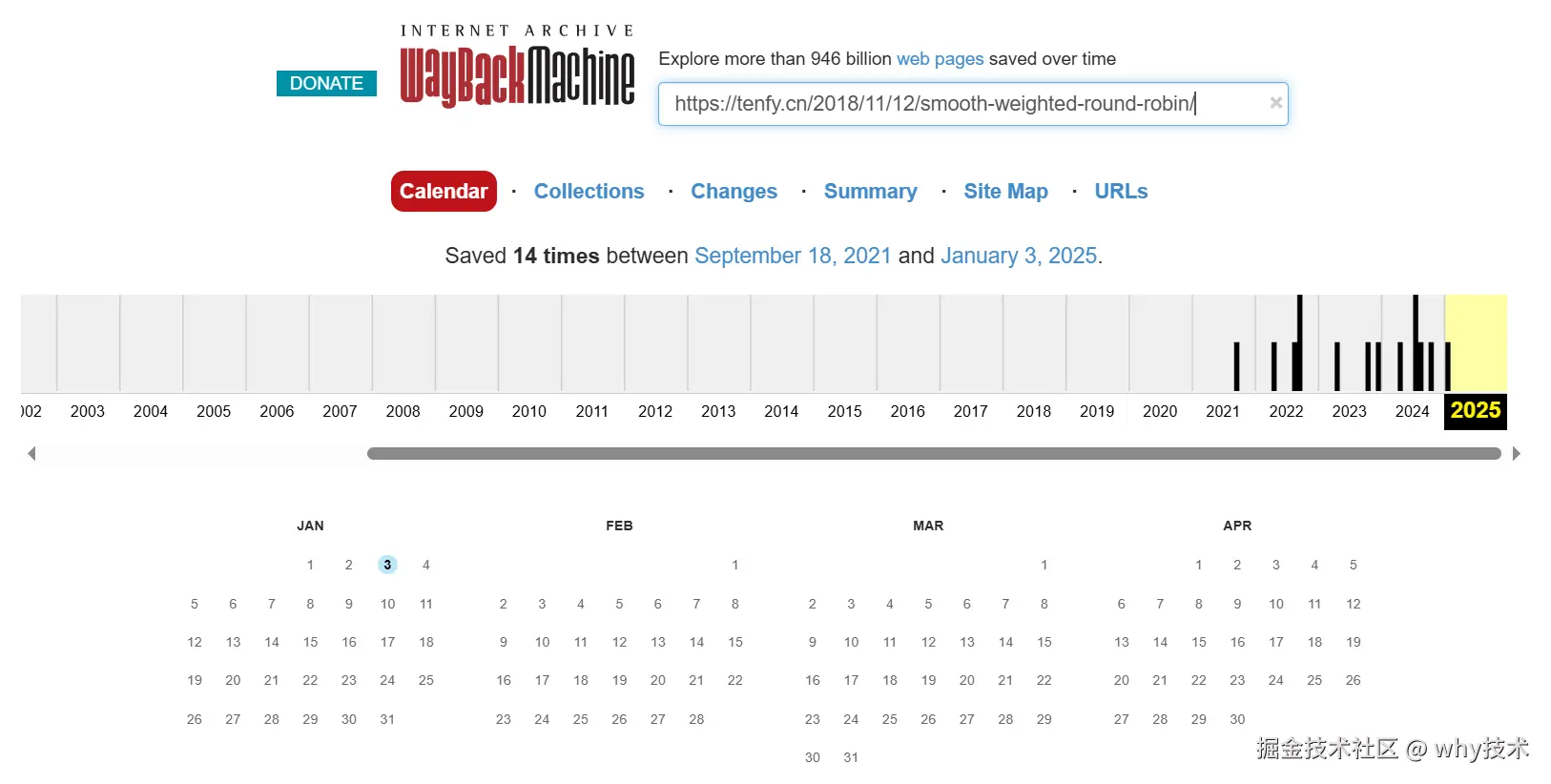
这个链接就能直接访问到当时还没被删除的原文:

但是我不知道为什么作者把这篇文章删除了?
难道是有什么漏洞?
不应该啊?
我感觉没毛病啊。
如果真的有漏洞,那么我这篇文章的证明部分也有一样的漏洞。
所以,如果你发现了有 BUG 的地方,或者有其他更加简单的证明方式、或者其他的参考文献什么的。
欢迎扔在评论区,我再学习学习。