LeetCode-542. 01 矩阵

1、题目描述

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

示例 1：

复制代码

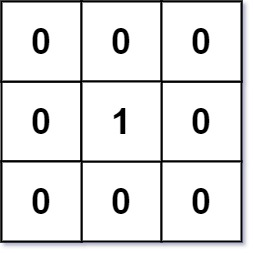
输入：mat = [[0,0,0],[0,1,0],[0,0,0]]
输出：[[0,0,0],[0,1,0],[0,0,0]]

示例 2：

复制代码

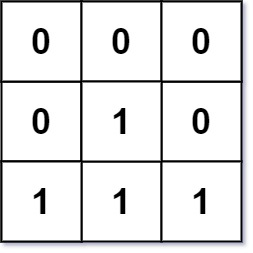
输入：mat = [[0,0,0],[0,1,0],[1,1,1]]
输出：[[0,0,0],[0,1,0],[1,2,1]]

提示：

m == mat.length
n == mat[i].length
1 <= m, n <= 104
1 <= m * n <= 104
mat[i][j] is either 0 or 1.
mat 中至少有一个 0

2、代码

cpp 复制代码

#include <queue>    
#include <utility>  
#include <vector>   
using namespace std;

class Solution
{
  public:
    // 计算矩阵中每个元素到最近0的距离
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat)
    {
        int row = mat.size();     
        int col = mat[0].size();  

        vector<vector<int>> ret(row, vector<int>(col, -1));
        
        // BFS队列，用于存储待处理的坐标（宽搜的核心数据结构）
        queue<pair<int, int>> q;

        // 第一步：初始化所有0的位置
        for (int i = 0; i < row; ++i) {
            for (int j = 0; j < col; ++j) {
                if (mat[i][j] == 0) {
                    ret[i][j] = 0;   // 0到自身的距离为0
                    q.push({i, j});  // 将所有0的坐标加入队列，作为BFS的起点
                }
            }
        }

        // 定义四个方向的偏移量：上、下、左、右（用于遍历相邻单元格）
        vector<pair<int, int>> dirs = {{-1, 0},
                                       {1, 0},  
                                       {0, -1},
                                       {0, 1}};  

        // 第二步：多源BFS扩散计算距离
        while (!q.empty()) {
            // 取出队列头部的坐标（当前处理的单元格）
            auto [i, j] = q.front();

            // 遍历四个相邻方向
            for (auto [x, y] : dirs) {
                // 计算相邻单元格的坐标
                int dx = i + x;  // 新行坐标 = 当前行 + 方向偏移
                int dy = j + y;  // 新列坐标 = 当前列 + 方向偏移

                // 检查相邻单元格是否有效：
                // 1. 不超出矩阵边界（行和列都在有效范围内）
                // 2. 该位置尚未计算距离（ret[dx][dy] == -1）
                if ((dx >= 0 && dx < row) && (dy >= 0 && dy < col) &&
                    (ret[dx][dy] == -1)) {
                    // 相邻单元格的距离 = 当前单元格距离 + 1（因为相邻）
                    ret[dx][dy] = ret[i][j] + 1;
                    // 将新计算的单元格加入队列，用于后续扩散
                    q.push({dx, dy});
                }
            }
            // 处理完当前单元格后出队
            q.pop();
        }

        // 返回计算好的距离矩阵
        return ret;
    }
};

3、解题思路

初始化部分：通过双重循环找到所有 0 的位置，将其距离设为 0 并加入队列，作为 BFS 的多源起点。
方向数组：定义了上下左右四个方向的偏移量，避免了重复编写判断相邻单元格的代码。
BFS 核心逻辑 ：
- 从队列中取出当前单元格，遍历其四个相邻位置
- 对每个有效且未计算距离的相邻单元格，更新其距离（当前距离 + 1）并加入队列
- 保证每个单元格只被计算一次，且首次计算的距离就是到最近 0 的最短距离
为什么有效：同时将所有 0 作为起点（距离为 0）从 0 开始向外扩散，每个 1 被首次访问时，一定是被最近的 0所扩散到的，因此首次计算的距离就是最短距离