文章目录
前言
本文介绍了Dijkstra最短路径算法及其应用。首先指出BFS算法在求单源最短路径时的局限性,仅适用于无权图或权值相同的图。然后详细阐述了Dijkstra算法的实现思路:通过维护三个数组(标记已找到最短路径、最短路径长度、前驱顶点),逐步确定各顶点的最短路径。算法步骤包括初始化数组、选择当前最短路径顶点、更新相邻顶点信息等。最后通过具体案例演示了算法执行过程,展示了如何通过迭代更新找到从起点到各顶点的最短路径。Dijkstra算法是解决带权图最短路径问题的经典方法,在数据结构等领域有重要应用。
一.迪杰斯特拉
- 艾兹格·W·迪杰斯特拉Edsger Wybe Dijkstra(1930~2002)
- 提出"goto有害理论"------操作系统,虚拟存储技术(5分)
- 信号量机制PV原语------操作系统,进程同步(15分)
- 银行家算法------操作系统,死锁(15分)
- 解决哲学家进餐问题------操作系统,死锁(15分)
- Dijkstra最短路径算法------数据结构大题、小题(10分)
二.BFS算法的局限性
1.例子

- 比如说我们要求g港到其他这些顶点的最短路径,那么按照广度优先算法,我们找到的g港到r城的最短路径是10
- 但事实上还有一条更短的就是我们可以先经过p城,然后再从p城再到r城下边这一条路径的总长度只有7这么多
2.结论
- BFS算法求单源最短路径只适用于无权图,或所有边的权值都相同的图
知识小回顾:带权路径长度(路径长度)------当图是带权图时,一条路径上所有边的权值之和,称为该路径的带权路径长度
三.Dijkstra算法
1.思路
- 选一个顶点作为起始顶点
- 初始化三个数组,分别存储标记各顶点是否已找到最短路径,最短路径长度,路径上的前驱
- 对选中的顶点的所有出边进行比较得到权值最小的弧将其标记为已经找到最短路径,最短路径就是那条弧的权值,其前驱为当前选中的顶点
- 将最近处理的顶点作为新选中的顶点,通过其出边更新三个数组中没有找到最短路径的顶点对应的数值,更新条件是,当当前路径长度(起始顶点到新选中顶点的下一个顶点)比原最短路径长度(起始顶点到新选中的顶点)小
- 循环上述过程,直到处理完所有顶点为止
2.例子(无向图与有向图思路一样)
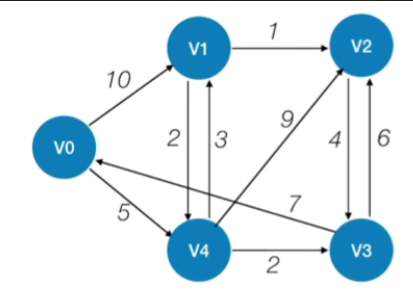
-
定义
- 假设现在是要找到V0到其他各个顶点的最短路径,定义三个数组
- 第一个数组表示的是我们目前为止有没有找到从V0到达这些个顶点的最短路径
- 第二个数组表示我们目前为止能够找到的最短的最优的一条路径总共的长度是多少
- 第三个数组用于记录每一个顶点在最短路径上的直接前驱

-
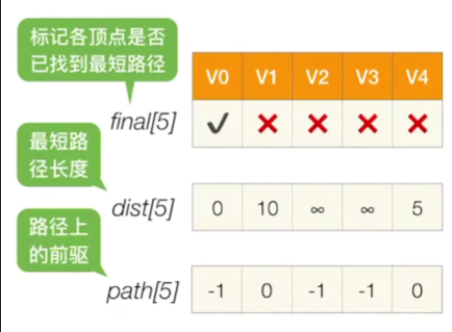
初始化
- V0对应的这个final值设为true
- 因为V0本身就是起点,所以从它到它自身的最短路径肯定就是0,所以V0的dist值为0
- 那刚开始的时候我们能够找到一条V0到V1的边,所以目前来看从V0到V1最短的一条路径,我们可以认为有可能是10这条路径,因此V1对应的dist值为10
- 那V4和V0也有一条相连的边,按照上面的思路,其dist值为5,其余没有与V0直接相连的顶点设为∞
- V1这个顶点,我们刚开始能够确定的比较好的一条路是从V0过来的,所以我们把V1的这个pass值设为0,表示的是目前能够找到的最好的一条路径是从V0到V1
- V4也是一样,path设为0,其余暂时没有路径上前驱的顶点path值默认为-1
-
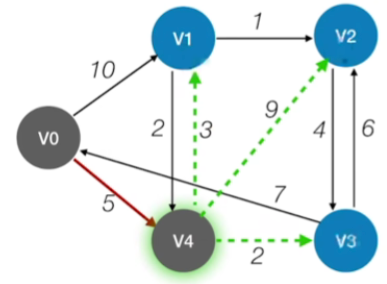
第一轮循环
-
循环遍历所有的这些节点相关的数组信息,要从中找到目前还没有确定最短路径,也就是说final值为false同时dist这个值最小的一个顶点
-
那显然在V1,V2,V3,V4这四个顶点当中,我们可以找到的最小的dist值应该是5, 所以我们选定V4这个顶点,然后把它的final值设为true,表示的是说我现在已经可以确定对于V4这个顶点来说,它的最短路径长度就是5这么多,并且它的直接前驱是V0,因此现在我们就确定了V0到V4的最短路径[1](#1)

-
接下来要检查所有和V4相连的顶点,那也就是V1,V2,V3这几个顶点,对于这几个顶点来说,如果从V4过来的话,那么有没有可能比之前找到的这条路径更短呢
-
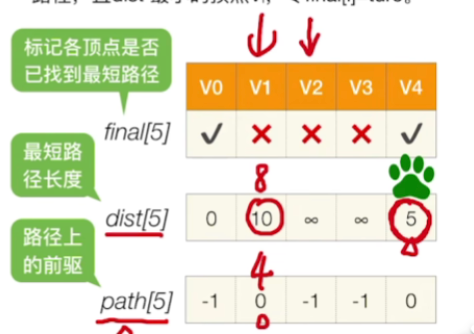
先来看V1这个顶点,我们之前可以确定的比较好的一条路长度为10,但现在我们可以确定从V0到V4其实有一条长度为5的路径(dist[4] = 5),而从V4再到V1,其实有一条长度为3的路径,因此如果V1顶点是从V4过来的话,那么我们就可以找到一条总长度为5+3=8的路径
-
那这条路径显然要比我们刚开始找的那条要更好,所以我们会把V1的这个dist的值改为8,同时把path的值改为4,也就是说目前能够找到的从V0到V1的最短路径总长度是8,而这条路径是从4号顶点过来的
-
V2也是一样,之前我们其实根本就没有找到能够从原点到达V2的路径,但是现在如果我们经过V4在到达V2的话,那我们就能够找到一条权值为5+9=14的路径,所以我们把V2的dist值修改为14,那path值也是设为4
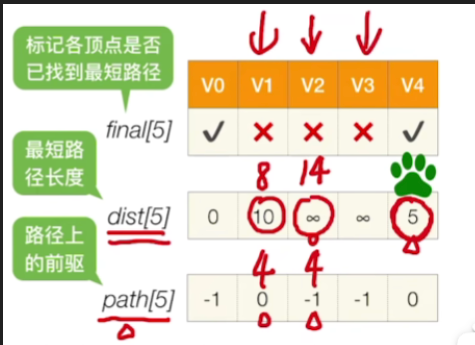
-
V3也是一样的操作,不做赘述
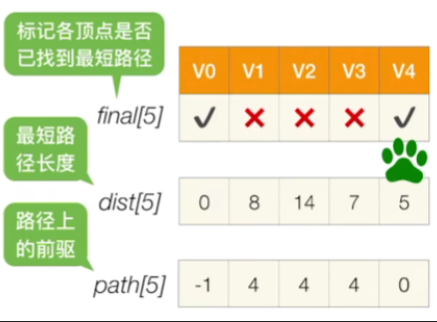
-
-
重复第一轮的操作,直到所有的顶点被处理完为止,结果如下
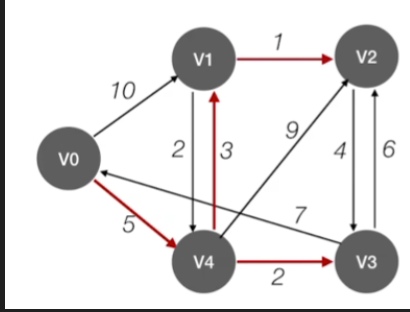
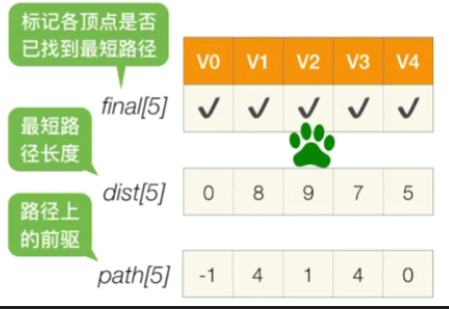
3.使用方法
- 比如说我们此时要找到V2这个顶点的最短路径
- 那么通过查dist数组可以知道最短的一条路径总长度应该是9
- 接下来通过path数组可以查到这条路径的完整信息,V2<---V1<---V4<---V0
4.代码实现思路
- 若从 V 0 V_{0} V0开始,令 f i n a l [ 0 ] = t u r e ; d i s t [ 0 ] = 0 ; p a t h [ 0 ] = − 1 final[0]=ture; dist[0]=0; path[0]=-1 final[0]=ture;dist[0]=0;path[0]=−1
其余顶点 f i n a l [ k ] = f a l s e ; d i s t [ k ] = a r c s [ 0 ] [ k ] ; p a t h [ k ] = ( a r c s [ 0 ] [ k ] = = ∞ ) ? − 1 : 0 final[k]=false; dist[k]=arcs[0][k]; path[k]=(arcs[0][k]==∞)?-1:0 final[k]=false;dist[k]=arcs[0][k];path[k]=(arcs[0][k]==∞)?−1:0 - n-1 轮处理:循环遍历所有顶点,找到还没确定最短路径,且 dist 最小的顶点 V i V_i Vi,令 f i n a l [ i ] = t u r e final[i]= ture final[i]=ture。并检查有邻接自 V i V_i Vi 的顶点,对于邻接自 V i V_i Vi 的顶点 V j V_j Vj,若 f i n a l [ i ] = f a l s e final[i]= false final[i]=false 且 d i s t [ i ] + a r c s [ i ] ] < d i s t [ i ] dist[i]+ arcs[i]]< dist[i] dist[i]+arcs[i]]<dist[i],则令 dist [ j ] = dist [ i ] + arcs [ i ] [ j ] ; p a t h [ j ] = i \text{ dist}[j]=\text{ dist}[i]+\text{ arcs}[i][j];path[j]=i dist[j]= dist[i]+ arcs[i][j];path[j]=i。(注: arcs [ i ] [ j ] \text{ arcs}[i][j] arcs[i][j] 表示 V i V_i Vi 到 V j V_{j} Vj 的弧的权值)
注: a r c s [ i ] [ j ] arcs[i][j] arcs[i][j]顶点i到达顶点j的弧的长度
5.时间复杂度
1.推导
- 在每一轮的处理当中,我们都需要循环遍历所有的这些顶点,找到一个dist值最小的顶点,也就是说我们每一轮的处理其实都需要把这些数组给扫一遍,数组总长度为|V|,所以从这个数组当中找出dist值最小的顶点应该是需要O|V|这样的时间复杂度
- 另外除了找到最小的dist值之外,我们还需要把这一轮选中的这个顶点,要检查和它相邻的其他的所有的顶点,那如果这个图是采用邻接矩阵存储的话,那要找到从一个顶点出发能够到达的其他顶点,就是要扫描和这个顶点相关的那一整行,时间复杂度为O|V|
- 所以每一轮的处理总共需要的时间,复杂度应该是两倍的2O|V|那可以舍弃常数项为O|V|
- 如果是用邻接表来存储的话,那么扫描和某一个顶点相连的这些出边所需要的时间就不需要O|V|这么多,不过由于找到最小的dist值,肯定都得扫描一遍整个数组,所以整体来看这一轮的处理总的时间复杂度也会达到O|V|这个量级
- 而我们总共需要|V|-1轮处理,所以整个算法的时间复杂度就应该是(|V|-1)O(|V|),即 O ∣ ( V ∣ 2 ) O|(V|^2) O∣(V∣2)
2.结论
- O(|V|²)
四.对比:Prim算法的实现思想
- 这个算法其实和我们之前讲的普里姆算法,它的实现思想是很类似的
- 只不过普里姆算法当中,lowCost数组它记录的是这些顶点加入到我们目前组建的这颗生成树里的最小代价
- 而迪杰斯特拉算法的dist数组记录的是从当前顶点到达某一个指定顶点的最短路径的值
- 但其实dist和普利姆的loCost这两个数组的作用是很类似的
- 由于算法的执行过程类似,所以普里姆算法和迪基斯特拉他们的时间复杂度也是相同的
五.用于负权值带权图
1.例子
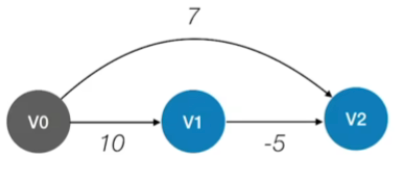
- 如果说我们的这个带权图里有这种负权值的边的话,那迪杰斯特拉算法就有可能会失效
- 如:我们要找到从V0到其他各个顶点的最短路径
-
那么按照算法的规则,初始的时候我们会把这几个数组设置为以下图片的值
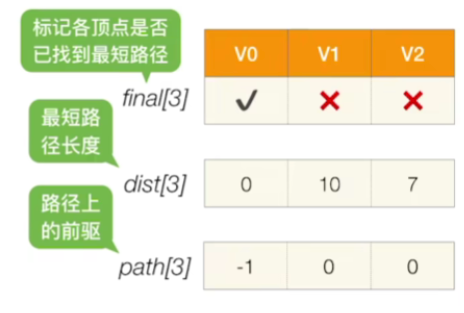
-
那目前来看暂时还没有确定最短路径的这些顶点当中能够找到的最小dist值应该是7,所以接下来我们可以确定V2这个顶点的最短路径长度是7,是从0号顶点直接过来的
-
那再下一轮是不是就只剩下V1,所以接下来是确定V1也是从V0过来的
-
但事实上事实上如果说我们从V0到V1再到V2,那由于这个弧它的权值是-5,所以整条路径的带权路径长度总和应该是10 - 5 = 5 < 7
-
因此对于V2这个顶点,其实我们找到7的这一条并不是最优的
-
2.结论
- Dijkstra 算法不适用于有负权值的带权图
结语
一更😉
如果想查看更多章节,请点击:一、数据结构专栏导航页
- 这是很简单的一个推理,当找到V0权值最小的弧时,由于其它弧的权值都比它的权值大,因此无论是从哪一条其他弧出发到达它相连的顶点,都会比通过它的权值大,所以它必定是其相连顶点的最短路径 ↩︎