深度学习-----《PyTorch神经网络高效训练与测试：优化器对比、激活函数优化及实战技巧》

一、训练过程

并行批量训练机制
- 一次性输入64个批次数据，创建64个独立神经网络并行训练。
- 所有网络共享参数（Ω），更新时计算64个批次的平均损失，统一更新全局参数。
梯度更新策略
- 使用torch.no_grad()上下文管理器清理反向传播产生的临时数据，优化内存利用。
多轮训练重要性
- 单轮训练（6万张图片）仅能获得19.22%正确率，需通过循环训练集（如10轮）提升模型收敛性。
- model.train()模式确保参数持续更新，避免重复初始化。

二、测试过程

测试集评估逻辑
- 输入测试数据后，前向传播得到预测结果，通过argmax提取最大概率对应的类别。
- 统计预测正确的数量，计算正确率（Correct / Total Test Samples）。
损失值与正确率的关系
- 测试阶段仍会计算损失值，但非核心指标；正确率（如70.04%）为模型性能的关键衡量标准。
资源管理优化
- 使用with torch.no_grad()减少冗余计算，提升测试效率。

三、关键实现细节

数据预处理
- 测试数据需明确设备（GPU/CPU），通过to(device)确保设备一致性。
预测结果处理
- 将预测概率转换为类别标签，对比真实标签统计正确率。
训练效率优化
- 设置打印间隔（如每100批次输出一次损失值），平衡调试需求与训练速度。

四、实践要点

超参数调整：通过增加训练轮数（如从10轮扩展至50轮）可显著提升模型性能。
验证集作用：测试集主要用于评估最终模型效果，而非实时调参。
竞赛策略：合理分配训练时间，确保比赛前完成高效模型迭代。

五、关键代码片段

1. 批量梯度下降训练核心代码

python 复制代码

# 初始化模型参数 Ω
model = MyNeuralNetwork().to(device)  # device为'cuda'或'cpu'
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
criterion = torch.nn.CrossEntropyLoss()  # 分类任务损失函数

# 训练循环
for epoch in range(num_epochs):
    for batch_idx, (inputs, labels) in enumerate(train_loader):
        # 前向传播
        outputs = model(inputs)
        loss = criterion(outputs, labels)
        
        # 反向传播 + 参数更新
        optimizer.zero_grad()  # 清空梯度缓存
        loss.backward()        # 反向传播计算梯度
        optimizer.step()       # 更新参数 Ω
        
        # 每100批次打印一次损失值
        if batch_idx % 100 == 0:
            print(f"Epoch {epoch}, Batch {batch_idx}: Loss = {loss.item()}")

2. 多轮训练扩展

python 复制代码

# 外层循环控制训练轮数
for epoch in range(num_epochs):
    # 内层循环执行单轮训练（6万张图片）
    for inputs, labels in train_loader:
        # ...（同上训练逻辑）...
    # 每轮结束后测试模型
    test_accuracy = evaluate_model(model, test_loader)
    print(f"Epoch {epoch+1} Test Accuracy: {test_accuracy}")

3. 测试集评估代码

python 复制代码

def evaluate_model(model, test_loader):
    correct = 0
    total = 0
    with torch.no_grad():  # 禁用梯度计算以节省内存
        for inputs, labels in test_loader:
            inputs = inputs.to(device)  # 确保数据在正确设备上
            labels = labels.to(device)
            outputs = model(inputs)     # 前向传播
            _, predicted = torch.max(outputs.data, 1)  # argmax获取预测类别
            total += labels.size(0)      # 统计总样本数
            correct += (predicted == labels).sum().item()  # 统计正确数
    return correct / total  # 返回准确率

4. 关键优化点说明

设备兼容性 ：通过inputs.to(device)统一数据与模型的设备（CPU/GPU）
资源管理 ：with torch.no_grad()减少测试阶段的内存占用
批量处理 ：64个批次并行训练加速收敛（需调整DataLoader的batch_size）

六、核心问题

训练效率低：原模型使用随机梯度下降（SGD）优化器，需100轮训练才能达到98%正确率，耗时约10分钟；改用Adam优化器后，仅需10轮训练即可达到96.81%正确率。

梯度消失问题：Sigmoid激活函数的导数范围（0~0.25）导致多层网络参数更新停滞，损失值在局部震荡无法收敛45。

七、关键知识点

1. 优化器改进：从SGD到Adam

原理：
- SGD每次用全部数据更新参数，易陷入局部最优且收敛慢；
- Adam通过自适应学习率和动量机制加速收敛，避免SGD的"高方差"问题。

代码示例：

python 复制代码

# 原SGD优化器（需修改）
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

# 改为Adam优化器
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

2. 学习率影响

现象：固定学习率（如0.01）导致训练后期损失值震荡，无法逼近全局最优；
解决思路：动态调整学习率（如学习率衰减），但需后续章节展开。

3. 激活函数优化：Sigmoid → ReLU

梯度消失原因 ：
- Sigmoid导数范围（0~0.25）导致多层网络参数更新时梯度逐层衰减至0；
- 数学表达：
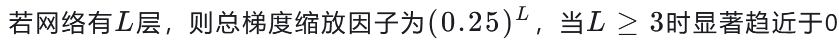
ReLU优势 ：
- 计算简单，加速训练

代码示例：

python 复制代码

# 原Sigmoid激活函数（需修改）
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# 改为ReLU激活函数
def relu(x):
    return np.maximum(0, x)

八、实验结果对比

九、扩展思考

深层网络适配性：ReLU在超过3层的网络中表现优异，是现代深度学习的基础激活函数
优化器组合：AdamW（带权重衰减的Adam）可缓解过拟合，适合迁移学习场景