并行多核体系结构基础——共享存储并行编程与针对链式数据结构的并行编程（笔记）

目录

• 三、共享存储并行编程
• • [3.1 并行编程步骤](#3.1 并行编程步骤)
  • [3.2 依赖分析](#3.2 依赖分析)
  • • [3.2.1 循环级依赖分析](#3.2.1 循环级依赖分析)
    • [3.2.2 迭代空间遍历图和循环传递依赖图](#3.2.2 迭代空间遍历图和循环传递依赖图)
  • [3.3 识别循环依赖中的并行任务](#3.3 识别循环依赖中的并行任务)
  • • [3.3.1 循环迭代间的并行和DOALL并行](#3.3.1 循环迭代间的并行和DOALL并行)
    • [3.3.2 DOACROSS：循环迭代间的同步并行](#3.3.2 DOACROSS：循环迭代间的同步并行)
    • [3.3.3 循环中语句间的并行](#3.3.3 循环中语句间的并行)
    • [3.3.4 DOPIPE循环中语句间的流水线并行](#3.3.4 DOPIPE循环中语句间的流水线并行)
  • [3.4 识别其他层面的并行](#3.4 识别其他层面的并行)
  • [3.5 确定变量的范围](#3.5 确定变量的范围)
  • • [3.5.1 私有化](#3.5.1 私有化)
    • [3.5.2 归约变量和操作](#3.5.2 归约变量和操作)
    • [3.5.3 准则](#3.5.3 准则)
  • [3.6 同步](#3.6 同步)
  • [3.7 任务到线程的映射](#3.7 任务到线程的映射)
  • • [3.7.1 静态与动态分配](#3.7.1 静态与动态分配)
    • [3.7.2 固有通信与人为通信](#3.7.2 固有通信与人为通信)
  • [3.8 线程到处理器的映射](#3.8 线程到处理器的映射)
  • [3.9 OpenMP概述](#3.9 OpenMP概述)
• 四、针对链式数据结构的并行编程
• • [4.1 LDS并行化所面临的挑战](#4.1 LDS并行化所面临的挑战)
  • [4.2 LDS并行化技术](#4.2 LDS并行化技术)
  • • [4.2.1 计算并行化与遍历](#4.2.1 计算并行化与遍历)
  • [4.3 针对链表的并行化技术](#4.3 针对链表的并行化技术)
  • • [4.3.1 使用共享锁与互斥锁对LDS节点操作并行](#4.3.1 使用共享锁与互斥锁对LDS节点操作并行)
    • [4.3.2 LDS遍历中的并行](#4.3.2 LDS遍历中的并行)
    • [4.4 事务内存](#4.4 事务内存)
• 参考文献

三、共享存储并行编程

3.1 并行编程步骤

依靠算法/代码：

1. 识别并行任务
2. 确定变量范围（小任务合并为大任务）
3. 必要的话插入同步

（机器独立）

---

（机器依赖）

4. 将任务分配给线程
5. 将线程映射到处理器

3.2 依赖分析

S S S表示一个语句或者一组语句。 S 1 → S 2 S1 \rightarrow S2 S1→S2表示程序执行中， S 1 S1 S1先于 S 2 S2 S2出现，那么：

• S 1 → T S 2 S1 \rightarrow^T S2 S1→TS2：表示真依赖 ，即 S 1 S1 S1写入 S 2 S2 S2读取位置
• S 1 → A S 2 S1 \rightarrow^A S2 S1→AS2：表示反依赖 ，即 S 1 S1 S1读取 S 2 S2 S2写入位置
• S 1 → O S 2 S1 \rightarrow^O S2 S1→OS2：表示输出依赖 ，即 S 1 S1 S1写入 S 2 S2 S2写入的同一位置

S1 x = 2;
S2 y = x;
S3 y = x + z;
S4 z = 6;

上述逻辑中，

• S 1 → T S 2 S1 \rightarrow^T S2 S1→TS2
• S 1 → T S 3 S1 \rightarrow^T S3 S1→TS3
• S 3 → A S 4 S3 \rightarrow^A S4 S3→AS4
• S 2 → O S 3 S2 \rightarrow^O S3 S2→OS3

反依赖 与输出依赖 又称为假依赖 ，后续指令不依赖于先前指令产生的任何值，并行程序中消除假依赖 一般通过私有化。
真依赖一般难以消除，他们是并行化的障碍。

3.2.1 循环级依赖分析

定义 [ i , j ] [i,j] [i,j]表示循环迭代空间。循环上层迭代 i i i次，内存循环迭代 j j j次。

for(i=1;i<n;i++){
S1: a[i] = a[i-1] + 1;
S2: b[i] = a[i];
}
for(i=1;i<n;i++)
	for(j=1;j<n;j++)
	S3: a]i][j] = a[i][j-1] + 1;
for(i=1;i<n;i++)
	for(j=1;j<n;j++)
	S4: a]i][j] = a[i-1][j] + 1;

依赖关系如下：

• S 1 [ i ] → T S 1 [ i + 1 ] S1[i] \rightarrow^T S1[i+1] S1[i]→TS1[i+1]
• S 1 [ i ] → T S 2 [ i ] S1[i] \rightarrow^T S2[i] S1[i]→TS2[i]
• S 3 [ i , j ] → T S 3 [ i , j + 1 ] S3[i,j] \rightarrow^T S3[i,j+1] S3[i,j]→TS3[i,j+1]
• S 4 [ i , j ] → T S 4 [ i + 1 , j ] S4[i,j] \rightarrow^T S4[i+1,j] S4[i,j]→TS4[i+1,j]

3.2.2 迭代空间遍历图和循环传递依赖图

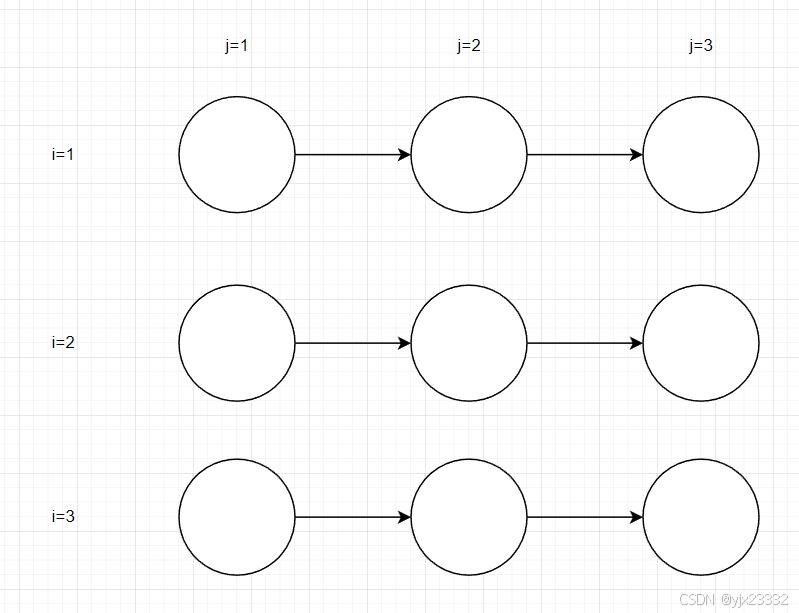
迭代空间遍历图（ITG）：以图形方式展示了迭代空间中的遍历顺序，不显示依赖性。

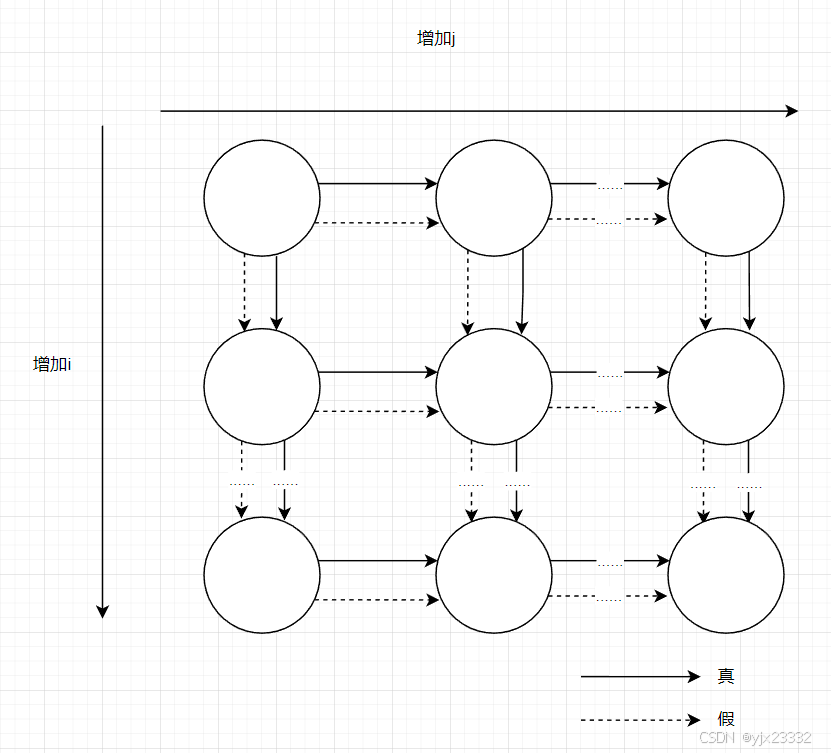
循环传递依赖图（LDG）：以图形方式展示了真/反/输出依赖，其中一个节点就是迭代空间中的一个点，而有向边显示依赖的方向。

for(i=1;i<4;i++)
	for(j=1;j<4;j++)
	S1: a]i][j] = a[i][j-1] + 1;

依赖关系为： S 1 [ i , j ] → T S 1 [ i , j + 1 ] S1[i,j] \rightarrow^T S1[i,j+1] S1[i,j]→TS1[i,j+1]

ITG

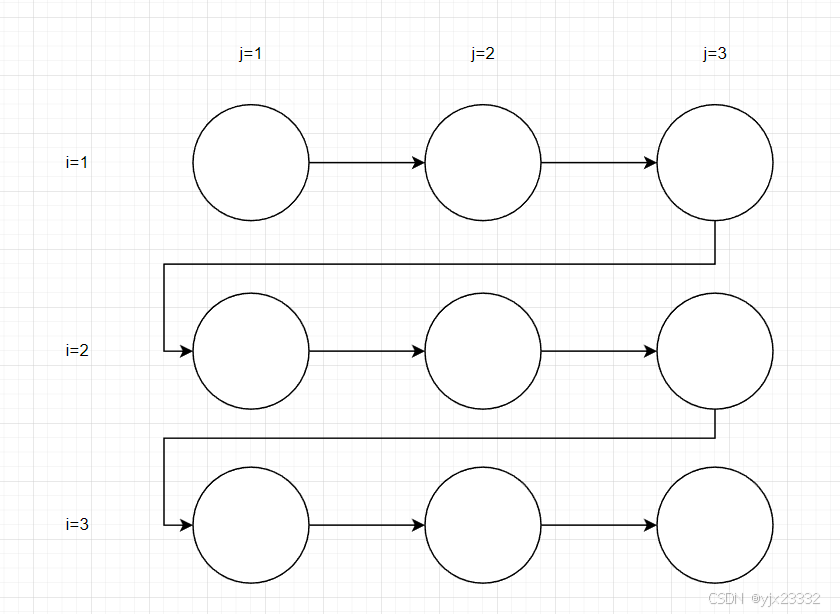
LDG

其中 → \rightarrow →为真依赖

for(i=1;i<=n;i++)
	for(j=1;j<=n;j++)
	S1: a]i][j] = a[i][j-1] + a[i][j+1] + a[i-1][j] + a[i+1][j];

依赖关系为：

• S 1 [ i , j ] → T S 1 [ i , j + 1 ] S1[i,j] \rightarrow^T S1[i,j+1] S1[i,j]→TS1[i,j+1]
• S 1 [ i , j ] → T S 1 [ i + 1 , j ] S1[i,j] \rightarrow^T S1[i+1,j] S1[i,j]→TS1[i+1,j]
• S 1 [ i , j ] → A S 1 [ i , j + 1 ] S1[i,j] \rightarrow^A S1[i,j+1] S1[i,j]→AS1[i,j+1]
• S 1 [ i , j ] → A S 1 [ i + 1 , j ] S1[i,j] \rightarrow^A S1[i+1,j] S1[i,j]→AS1[i+1,j]

注意，我们始终注意的是 S S S读取和写入的位置，即i,j始终表示的是等号左侧的值。

因此 S 1 [ i , j ] S1[i,j] S1[i,j]（我们设它为 x x x）的值会在 S 1 [ i , j + 1 ] S1[i,j+1] S1[i,j+1]与 S 1 [ i + 1 , j ] S1[i+1,j] S1[i+1,j]被读取（等号左侧）

而此时x对应的等号右侧 S 1 [ i , j + 1 ] S1[i,j+1] S1[i,j+1]与 S 1 [ i + 1 , j ] S1[i+1,j] S1[i+1,j]的值未被赋值，他们将会在等号左侧（相对当前i,j）为 S 1 [ i , j + 1 ] S1[i,j+1] S1[i,j+1]与 S 1 [ i + 1 , j ] S1[i+1,j] S1[i+1,j]时读取 x x x的值.

ITG

LDG

3.3 识别循环依赖中的并行任务

3.3.1 循环迭代间的并行和DOALL并行

for(i=2;i<=n;i++)
	S1: a]i] = a[i-2];

依赖关系为：

• S 1 [ i ] → T S 1 [ i + 2 ] S1[i] \rightarrow^T S1[i+2] S1[i]→TS1[i+2]

LDG

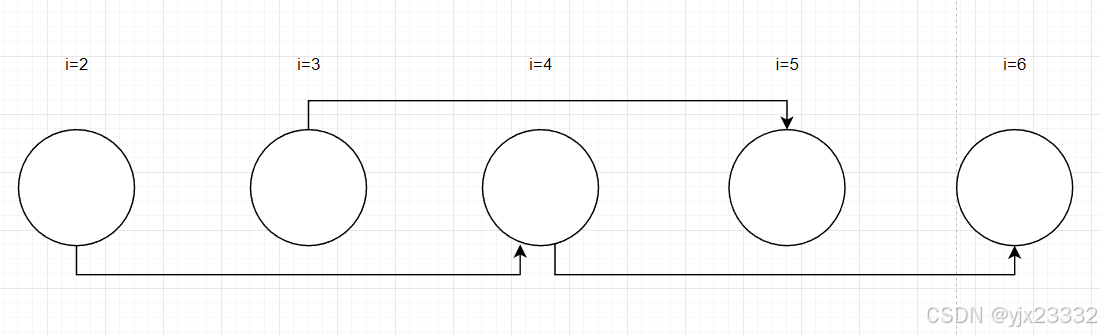
很容易发现，整个循环偶数和奇数各走各的，因此可以拆为两个并行循环。

• DOALL并行

当一个循环的所有迭代都是可并行的任务时（以某种循环执行时，循环流程中无黑实线），则该循环表现出DOALL并行。

for(i=1;i<=n;i++)
	for(j=1;j<=n;j++)
	S1: a]i][j] = a[i][j-1] + a[i][j+1] + a[i-1][j] + a[i+1][j];

这个LDG途中，以反对角线的方式进行循环将无黑实线

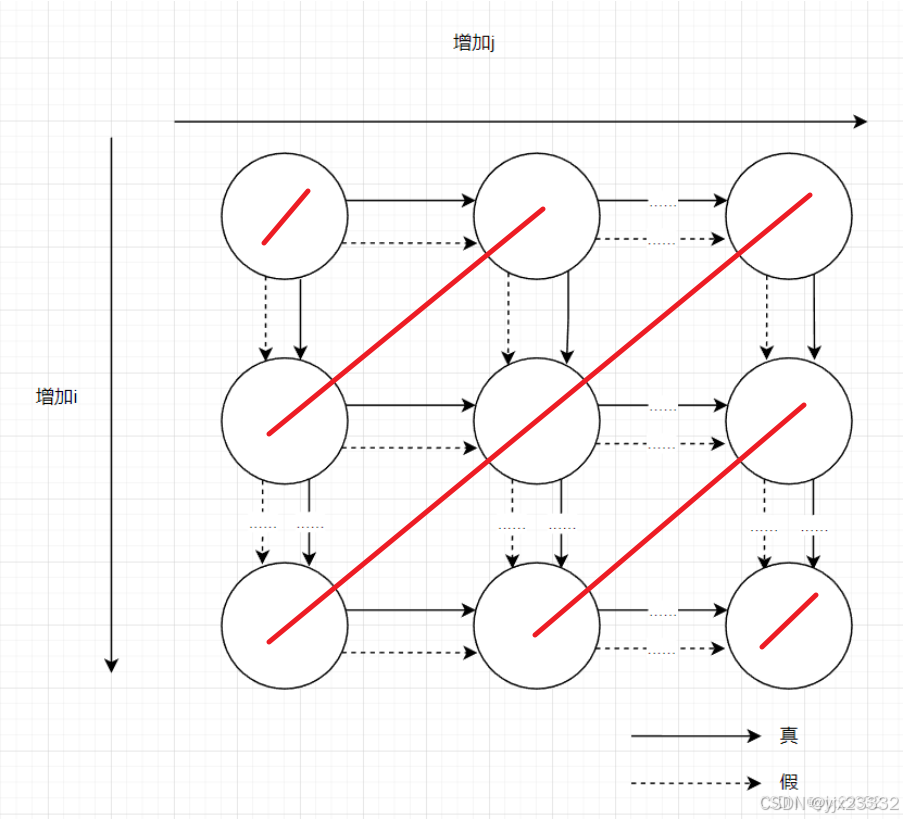
3.3.2 DOACROSS：循环迭代间的同步并行

因为DOALL并行循环中并行任务数量非常大，因此优先识别。

for(i=1;i<=N;i++)
S: a[i] = a[i-1] + b[i] * c[i];

依赖关系为：
S [ i ] → T S [ i + 2 ] S[i]\rightarrow^TS[i+2] S[i]→TS[i+2]

由于不能用DOALL并行，但是 b b b和 c c c没有参与循环，于是我们可以将其拆分为：

for(i=1;i<=N;i++)// DOALL并行
S1: temp[i] = b[i] * c[i];
for(i=1;i<=N;i++)
S2: a[i] = a[i-1] + temp[i];

• DOACROSS并行
  在具有部分循环依赖的循环中提取并行任务的解决方案是采用DOACROSS并行。其中每个迭代仍是并行任务，但是插入了同步以确保【使用者迭代】（consumer iteration）只读取【产生者迭代】（producer iteration）产生的数据。

上述式子优化后，可为：

post(0);
for(i=1;i<=N;i++){
S1: temp[i] = b[i] * c[i];
wait(i-1);
S2: a[i] = a[i-1] + temp[i];
post(i);
}

在所有循环都并行中，i次循环通过wait()等待i-1次循环执行完成，并将自己执行完成的值放入post()激活i+1次循环。

我们假设同步延迟为0， T S 1 T_{S1} TS1与 T S 2 T_{S2} TS2分别表示语句 S 1 S1 S1与 S 2 S2 S2的执行时间。

顺序执行总时间为：
N ∗ ( T S 1 + T S 2 ) N*(T_{S1}+T_{S2}) N∗(TS1+TS2)

DOACROSS并行总时间为：
T S 1 + N ∗ T S 2 T_{S1}+N*T_{S2} TS1+N∗TS2

即加速比：
N ∗ ( T S 1 + T S 2 ) T S 1 + N ∗ T S 2 \frac{N*(T_{S1}+T_{S2})}{T_{S1}+N*T_{S2}} TS1+N∗TS2N∗(TS1+TS2)
1 + 1 − 1 N 1 N + T S 2 T S 1 1+\frac{1-\frac{1}{N}}{\frac{1}{N}+\frac{T_{S2}}{T_{S1}}} 1+N1+TS1TS21−N1

N趋向无穷后，最终耗时可以简化为
1 + T S 1 T S 2 1+\frac{T_{S1}}{T_{S2}} 1+TS2TS1

由此可知实际改进了多少，取决于并行部分和串行部分的耗时比，以及同步时间。由于同步开销通常很大，使用DOACROSS并行时，尽量将许多同步任务放到同一个线程中，减少同步次数。

3.3.3 循环中语句间的并行

当一个循环具有循环传递依赖时，另一种并行化的方法是将一个循环分发（distribute）到几个循环中去。

for(i=1;i<=n;i++){
S1: a[i] = b[i+1]*a[i-1];
S2: b[i] = b[i]*coef;
S3: c[i] = 0.5*(c[i]+a[i]);
S4: d[i] = d[i-1]*d[i];
}

依赖为：

• S 1 [ i ] → T S 1 [ i + 1 ] S1[i]\rightarrow^TS1[i+1] S1[i]→TS1[i+1]
• S 4 [ i ] → T S 4 [ i + 1 ] S4[i]\rightarrow^TS4[i+1] S4[i]→TS4[i+1]
• S 1 [ i ] → A S 2 [ i + 1 ] S1[i]\rightarrow^AS2[i+1] S1[i]→AS2[i+1]
• S 1 [ i ] → T S 3 [ i ] S1[i]\rightarrow^TS3[i] S1[i]→TS3[i]

依据上可得，S4可以单独提出来，改为：

for(i=1;i<=n;i++){//循环1
S1: a[i] = b[i+1]*a[i-1];
S2: b[i] = b[i]*coef;
S3: c[i] = 0.5*(c[i]+a[i]);
}

for(i=1;i<=n;i++){//循环2
S4: d[i] = d[i-1]*d[i];
}

我们假设， T S 1 T_{S1} TS1、 T S 2 T_{S2} TS2、 T S 3 T_{S3} TS3、 T S 4 T_{S4} TS4分别表示语句 S 1 S1 S1、 S 2 S2 S2、 S 3 S3 S3、 S 4 S4 S4的执行时间。

加速比就为：

N ∗ ( T S 1 + T S 2 + T S 3 + T S 4 ) m a x ( N ∗ ( T S 1 + T S 2 + T S 3 ) , N ∗ T S 4 ) \frac{N*(T_{S1}+T_{S2}+T_{S3}+T_{S4})}{max(N*(T_{S1}+T_{S2}+T_{S3}),N*T_{S4})} max(N∗(TS1+TS2+TS3),N∗TS4)N∗(TS1+TS2+TS3+TS4)

如果 T S 1 T_{S1} TS1、 T S 2 T_{S2} TS2、 T S 3 T_{S3} TS3、 T S 4 T_{S4} TS4均为 T T T，则结果为：
N ∗ ( T S 1 + T S 2 + T S 3 + T S 4 ) m a x ( N ∗ ( T S 1 + T S 2 + T S 3 ) , N ∗ T S 4 ) = 4 N T m a x ( 3 N T , N T ) = 4 3 \frac{N*(T_{S1}+T_{S2}+T_{S3}+T_{S4})}{max(N*(T_{S1}+T_{S2}+T_{S3}),N*T_{S4})}=\frac{4NT}{max(3NT,NT)}=\frac{4}{3} max(N∗(TS1+TS2+TS3),N∗TS4)N∗(TS1+TS2+TS3+TS4)=max(3NT,NT)4NT=34

注意到， S 1 [ i ] → T S 1 [ i + 1 ] S1[i]\rightarrow^TS1[i+1] S1[i]→TS1[i+1]执行完成后， S 1 [ i ] → A S 2 [ i + 1 ] S1[i]\rightarrow^AS2[i+1] S1[i]→AS2[i+1]与 S 1 [ i ] → T S 3 [ i ] S1[i]\rightarrow^TS3[i] S1[i]→TS3[i]可以DOALL并行。

可调整代码为：

for(i=1;i<=n;i++){//并行循环1
S1: a[i] = b[i+1]*a[i-1];
}

for(i=1;i<=n;i++){//并行循环1
S4: d[i] = d[i-1]*d[i];
}

// 并行循环1结束后，再执行如下循环
for(i=1;i<=n;i++){//并行循环2
S2: b[i] = b[i]*coef;
}

for(i=1;i<=n;i++){//并行循环2
S3: c[i] = 0.5*(c[i]+a[i]);
}

如果 T S 1 T_{S1} TS1、 T S 2 T_{S2} TS2、 T S 3 T_{S3} TS3、 T S 4 T_{S4} TS4均为 T T T，此时加速比为：
N ∗ ( T S 1 + T S 2 + T S 3 + T S 4 ) m a x ( N ∗ T S 1 + m a x ( T S 2 , T S 3 ) , N ∗ T S 4 ) = 4 N T m a x ( ( N + 1 ) T , N T ) = 4 N T ( N + 1 ) T \frac{N*(T_{S1}+T_{S2}+T_{S3}+T_{S4})}{max(N*T_{S1}+max(T_{S2},T_{S3}),N*T_{S4})}=\frac{4NT}{max((N+1)T,NT)}=\frac{4NT}{(N+1)T} max(N∗TS1+max(TS2,TS3),N∗TS4)N∗(TS1+TS2+TS3+TS4)=max((N+1)T,NT)4NT=(N+1)T4NT

3.3.4 DOPIPE循环中语句间的流水线并行

如果存在传递依赖的情况，可以使用流水线并行：

for(i=1;i<=n;i++){
S1: a[i] = a[i-1]+b[i];
S2: c[i] = c[i]+a[i];
}

依赖为：

• S 1 [ i ] → T S 1 [ i + 1 ] S1[i]\rightarrow^TS1[i+1] S1[i]→TS1[i+1]
• S 1 [ i ] → T S 2 [ i ] S1[i]\rightarrow^TS2[i] S1[i]→TS2[i]

那么通过DOPIPE并行，可以改为：

for(i=1;i<=n;i++){
S1: a[i] = a[i-1]+b[i];
post(i);
}

for(i=1;i<=n;i++){
wait(i);
S2: c[i] = c[i]+a[i];
}

3.3.3中的例子

for(i=1;i<=n;i++){
S1: a[i] = b[i+1]*a[i-1];
S2: b[i] = b[i]*coef;
S3: c[i] = 0.5*(c[i]+a[i]);
S4: d[i] = d[i-1]*d[i];
}

DOPIPE并行的话，可以改为：

post(0);
for(i=1;i<=n;i++){//循环1
S1: a[i] = b[i+1]*a[i-1];
post(i);
}

for(i=1;i<=n;i++){//循环2
S4: d[i] = d[i-1]*d[i];
}

for(i=1;i<=n;i++){//循环3
wait(i-1);
S2: b[i] = b[i]*coef;
}

for(i=1;i<=n;i++){//循环4
wait(i);
S3: c[i] = 0.5*(c[i]+a[i]);
}

为减少DOPIPE并行的同步开销，我们可以每n次迭代后再post()一次，而不是每完成一次循环就同步一次

3.4 识别其他层面的并行

在针对非循环的程序逻辑中，我们可以将代码分成三组语句：

1. 函数调用之前（前置代码）
2. 要调用的每个函数（函数）
3. 调用函数之后（后置代码）

这三个代码间若缺少真依赖都会为并行带来机会。

int search_tree(struct tree *p,int data){
S1:
	int count = 0;
	if(p == NULL){
		return 0;
	}
	if(p->data == data){
		count = 1;
	}
S2:	count += search_tree(p->left);
S3:	count += search_tree(p->right);
S4:	return count;
}

依赖为：

• S 1 → T S 2 S1\rightarrow^TS2 S1→TS2
• S 1 → T S 3 S1\rightarrow^TS3 S1→TS3
• S 1 → T S 4 S1\rightarrow^TS4 S1→TS4
• S 2 → T S 3 S2\rightarrow^TS3 S2→TS3
• S 2 → T S 4 S2\rightarrow^TS4 S2→TS4
• S 3 → T S 4 S3\rightarrow^TS4 S3→TS4

通过重命名的方式，我们可以将依赖消减为：

int search_tree(struct tree *p,int data){
S1:	
	int count = 0;
	if(p == NULL){
		return 0;
	}
	if(p - data == data){
		count = 1;
	}
S2:	int count2 += search_tree(p->left);
S3:	int count3 += search_tree(p->right);
S4:	return (count1 + count2 + count3);
}

依赖为：

• S 1 → T S 4 S1\rightarrow^TS4 S1→TS4
• S 2 → T S 4 S2\rightarrow^TS4 S2→TS4
• S 3 → T S 4 S3\rightarrow^TS4 S3→TS4

此时S1、S2与S3就可以单独执行了

3.5 确定变量的范围

确定并行任务后，通常并行任务数量多于可用的处理器数量，因此多个任务再分配给线程执行之前经常会合并为较大任务。执行任务的线程数通常等于或小于可用处理器数量。本节先假设处理器数目无限。

将变量分为如下几类：

• 只读
• 读/写非冲突
• 读/写冲突

3.5.1 私有化

读/写冲突的变量阻碍并行，对此最主要就是将他们私有化。

可私有化的变量：

1. 在原始顺序程序执行次序中，变量由一个任务首先定义（或写入），然后才能被该任务使用（读取）。
2. 变量在被同一个任务读取之前没有被定义，但是任务应该从变量中读取的值是事先知道的。

3.5.2 归约变量和操作

归约是指将多个并行任务的私有化计算结果合并以形成最终结果。

3.5.3 准则

• 只读变量应声明为共享，避免可能降低性能的存储开销。

• 读/写非冲突变量也应声明为共享

• 读/写冲突的变量通常也应该声明为共享，但是要用临界区保护对它的访问（临界区是昂贵的），需要衡量私有化和临界区的代价。

  临界区：
  一次仅允许一个进程使用的共享资源

3.6 同步

同步操作不在任务间执行，而是在线程间。

同步的方式

1. 点对点同步：提交与等待的方式。等待线程会阻塞，直到对应的标记被提交后，才会继续执行（上述的DOACROSS与DOPIPE并行）
2. 锁同步：通过获取锁与释放锁的方式（排他锁），保证执行顺序。
3. 栅障：定义了一个点，所有线程都达到时才允许线程通过。（Java中的 CyclicBarrier和CountDownLatch）

3.7 任务到线程的映射

3.7.1 静态与动态分配

分配方式：

1. 静态分配：执行之前将任务固定分配给线程
2. 动态分配：任务在执行之前是不会分配给线程，依据线程是否空闲分配任务（线程池）。这会给任务队列管理带来额外开销

块大小：代表单个任务的连续迭代数量。

为了说明静态分配，我们假设总迭代数目： n = 8 n=8 n=8，线程数： p = 2 p=2 p=2，

sum = 0;
for(i=0;i<n;i++){
	for(j=0;j<=i;j++){
		sum += a[i][j];
	}
}
Print sum;

如果块大小为4时，线程1执行外层前4个迭代，线程2执行外层后4个迭代。

• 线程1的内层循环次数为： 1 + 2 + 3 + 4 = 10 1+2+3+4 = 10 1+2+3+4=10(因为内嵌循环j<=i，j随着i的增大而增大)
• 线程2的内层循环次数为： 5 + 6 + 7 + 8 = 26 5+6+7+8 = 26 5+6+7+8=26(因为内嵌循环j<=i，j随着i的增大而增大)

出现了不均衡调度。

但如果将块大小缩小至1，线程1执行外层奇数迭代，线程2执行外层偶数迭代。

• 线程1的内层循环次数为： 1 + 3 + 5 + 7 = 16 1+3+5+7 = 16 1+3+5+7=16
• 线程2的内层循环次数为： 2 + 4 + 6 + 8 = 20 2+4+6+8 = 20 2+4+6+8=20

不均衡有所缓减，因此如果循环迭代较多时，可以适当减小块大小。

3.7.2 固有通信与人为通信

1. 固有通信：任务映射对算法影响，主要体现算法本身对于通信的需求
2. 人为通信：任务映射对数据布局方式和架构影响，依赖于核的并行架构（基本可以认为是硬件层级）

固有通信的评估可以用：
通信 − 计算比率（ C C R ） 通信-计算比率（CCR） 通信−计算比率（CCR）
C C R = 线程通信量（单个线程对其他线程访问量） 单个线程计算量（ 输入规模 处理器数量 ） CCR=\frac{线程通信量（单个线程对其他线程访问量）}{单个线程计算量（\frac{输入规模}{处理器数量}）} CCR=单个线程计算量（处理器数量输入规模）线程通信量（单个线程对其他线程访问量）

人为通信：需要考虑在两个处理器之间来回交换数据。受数据交换频率和数据交换延迟影响。

3.8 线程到处理器的映射

最简单的方式为让操作系统线程调度器自己决定。但针对并行程序，要确保它的所有线程同时运行或这都不运行，来减少阻塞耗费的时间。

一些操作系统有成组调度功能，一组中的线程会被同时调度运行和等待。

此外将线程映射到处理器也是为了数据局部性，避免数据存储位置距离核较远问题。通过数据映射和线程到处理器的显式映射的方式解决。

• 数据映射的方式，有如下实现方式
  • 允许将数据分配或映射到访问该数据的线程所运行的节点。（比如C就可以）
  • 分配或迁移数据到访问该数据的线程。
• 线程到处理器的显式映射的方式则依赖于操作系统提供的接口
  • 比如linux的cset或者C在windows中的SetThreadAffinityMask(handle, mask)。

3.9 OpenMP概述

开放式多处理（Open Multi-Processing）是支持共享存储编程的应用编程接口（API）。

它支持C、C++和Fortran语言。通过OpenMP，开发者可以编写能够在多核心、多处理器计算机上高效运行的并行程序。OpenMP通过提供高层抽象的并行算法描述，降低了并行编程的难度和复杂度。当编译器不支持OpenMP时，程序会退化成普通（串行）程序，而程序中已有的OpenMP指令不会影响程序的正常编译运行。

也就是一套封装好的框架，可以较方便让程序有并行功能。

具体可以参考OpenMp

四、针对链式数据结构的并行编程

针对链式数据结构(LDS)的访问往往含有大量的循环传递依赖，因此针对链式数据结构需要不同的并行化技术。

4.1 LDS并行化所面临的挑战

链表、数、散列表、图等，链式数据结构的共同特点都是包含一组节点并且节点之间通过指针相互链接。

这也导致了循环级并行化的不足 ，要遍历链式数据结构。此外，如果在递归时出现环 ，且在之前的循环中修改了一些值，则会造成额外的循环传递依赖。以及递归遍历也是一个问题，针对一些数据结构可以调整为并行，但有一些却不行。

4.2 LDS并行化技术

4.2.1 计算并行化与遍历

简单的并行化LDS的方法为将计算的部分并行化（遍历过程不变）。

以单向链表为例。

数据结构为：

class Node {
    int data;
    Node next;
} 

# 非并行计算:
while(p!=null){
	compute(p);
	p = p.next;
}
# 并行计算
while(p!=null){
	new Thread(new Compute(p)).start();
	p = p.next;
}

4.3 针对链表的并行化技术

此处主要讨论的是针对线程间单节点的操作。

4.3.1 使用共享锁与互斥锁对LDS节点操作并行

该种方式的实现较简单，在LDS中，在增删改操作方法中添加写锁获取方法并在操作完成后释放锁；在读操作方法中添加获取读锁方法并在操作完成后释放锁。同时，需要实现读锁为共享锁可与其他读锁共存；写锁为互斥锁不与其他读锁、写锁共存。

4.3.2 LDS遍历中的并行

针对LDS遍历并行的实现，书中提出了两种（锁使用4.3.1中的读写锁）：

1. 细粒度：每个节点都关联一个锁变量，但管理锁的复杂度较高，容易死锁和活锁

   • 在遍历中锁住将被修改或者需要依赖其有效性的节点，比如删除通常需要写锁锁住上一节点，当前节点，读锁锁定下一节点
   • 修改节点
   • 释放节点

2. 粗粒度：使用全局锁保护整个LDS，但粒度太粗

   • 直接获取全局读写锁
   • 修改节点
   • 释放锁

4.4 事务内存

事务内存（TM）就是将每一个操作都封装进一个事务中。比如：atomic{Insert(...)}，这种类似的原子操作（乐观锁）。提交时如果发现冲突，就会回滚，在冲突较大时，代价较高。这个

另外，Java可以通过synchronized对方法进行简单的加锁，不过这是悲观锁。

参考文献

【1】《并行多核体系结构基础》【美】汤孟岩

【2】OpenMp