【知识杂记】卡尔曼滤波及其变种，从理论精要到工程实践深入解析

卡尔曼滤波公式推导，点击此处跳转

卡尔曼滤波：驾驭不确定性的最优估计

在不确定性充斥的现实世界中，如何从充满噪声的数据中，准确地估计出系统的真实状态？这就是卡尔曼滤波（Kalman Filter, KF）的革命性力量。它是一种巧妙融合预测 和测量的算法，能持续生成比任何单一信息源都更精确的、最优的实时状态估计。

1. 核心思想：预测-更新循环

卡尔曼滤波的运行基于一个优雅的递归循环，每一次迭代都包含两个关键步骤：

预测（Prediction）：

利用已知的系统动态模型，根据上一时刻的最优状态，预测当前时刻的状态和不确定性。这个预测是一个先验估计，因为它是在还没有新测量数据时进行的。由于模型本身的不确定性，预测过程总会增加不确定性。
更新（Update）：

当新的传感器测量值到来时，滤波器会用这个测量值来修正先前的预测。通过融合这两种信息，它能得到一个更精确的、不确定性更小的后验最优估计。

这个循环的核心是卡尔曼增益（Kalman Gain） 。这个增益是一个权重系数 ，它动态地决定了我们应该更相信预测模型，还是更相信传感器测量。如果预测的不确定性大而测量噪声小，卡尔曼增益就会变大，算法会更多地采纳测量值。反之，如果预测非常精确而测量噪声大，增益就会变小，算法会更多地依赖预测结果。

PS：根据卡尔曼增益公式可以更直观理解，R为量测噪声矩阵，且位于分母。 K k = P k ∣ k − 1 H k T ( H k P k ∣ k − 1 H k T + R k ) − 1 K_k = P_{k|k-1} H_k^T (H_k P_{k|k-1} H_k^T + R_k)^{-1} Kk=Pk∣k−1HkT(HkPk∣k−1HkT+Rk)−1。

2. 五大核心公式的物理直觉

卡尔曼滤波的数学核心由五大公式组成，它们描述了预测和更新的整个过程。

2.1 预测步骤

状态预测方程： 用上一时刻的最优状态 x ^ k − 1 ∣ k − 1 \hat{x}{k-1|k-1} x^k−1∣k−1 和系统模型 F k F_k Fk 来预测当前时刻的状态 x ^ k ∣ k − 1 \hat{x}{k|k-1} x^k∣k−1。
x ^ k ∣ k − 1 = F k x ^ k − 1 ∣ k − 1 + B k u k − 1 \hat{x}{k|k-1} = F_k \hat{x}{k-1|k-1} + B_k u_{k-1} x^k∣k−1=Fkx^k−1∣k−1+Bkuk−1
协方差预测方程： 预测不确定性。它表明，不确定性 P P P 会随着时间通过系统模型 F F F 传递，并被过程噪声 Q k Q_k Qk 放大。
P k ∣ k − 1 = F k P k − 1 ∣ k − 1 F k T + Q k P_{k|k-1} = F_k P_{k-1|k-1} F_k^T + Q_k Pk∣k−1=FkPk−1∣k−1FkT+Qk

2.2 更新步骤

卡尔曼增益方程： 计算权重。它权衡了预测的不确定性 P k ∣ k − 1 P_{k|k-1} Pk∣k−1 和测量噪声的不确定性 R k R_k Rk。
K k = P k ∣ k − 1 H k T ( H k P k ∣ k − 1 H k T + R k ) − 1 K_k = P_{k|k-1} H_k^T (H_k P_{k|k-1} H_k^T + R_k)^{-1} Kk=Pk∣k−1HkT(HkPk∣k−1HkT+Rk)−1
状态更新方程： 修正预测。它利用卡尔曼增益，将实际测量值 z k z_k zk 与预测测量值之间的差异（被称为"新息"）添加到预测状态中进行修正。
x ^ k ∣ k = x ^ k ∣ k − 1 + K k ( z k − H k x ^ k ∣ k − 1 ) \hat{x}{k|k} = \hat{x}{k|k-1} + K_k(z_k - H_k \hat{x}_{k|k-1}) x^k∣k=x^k∣k−1+Kk(zk−Hkx^k∣k−1)
协方差更新方程： 降低不确定性。在引入新测量值后，不确定性会减小。这个方程表明，后验协方差 P k ∣ k P_{k|k} Pk∣k 总是小于先验协方差 P k ∣ k − 1 P_{k|k-1} Pk∣k−1。
P k ∣ k = ( I − K k H k ) P k ∣ k − 1 P_{k|k} = (I - K_k H_k)P_{k|k-1} Pk∣k=(I−KkHk)Pk∣k−1

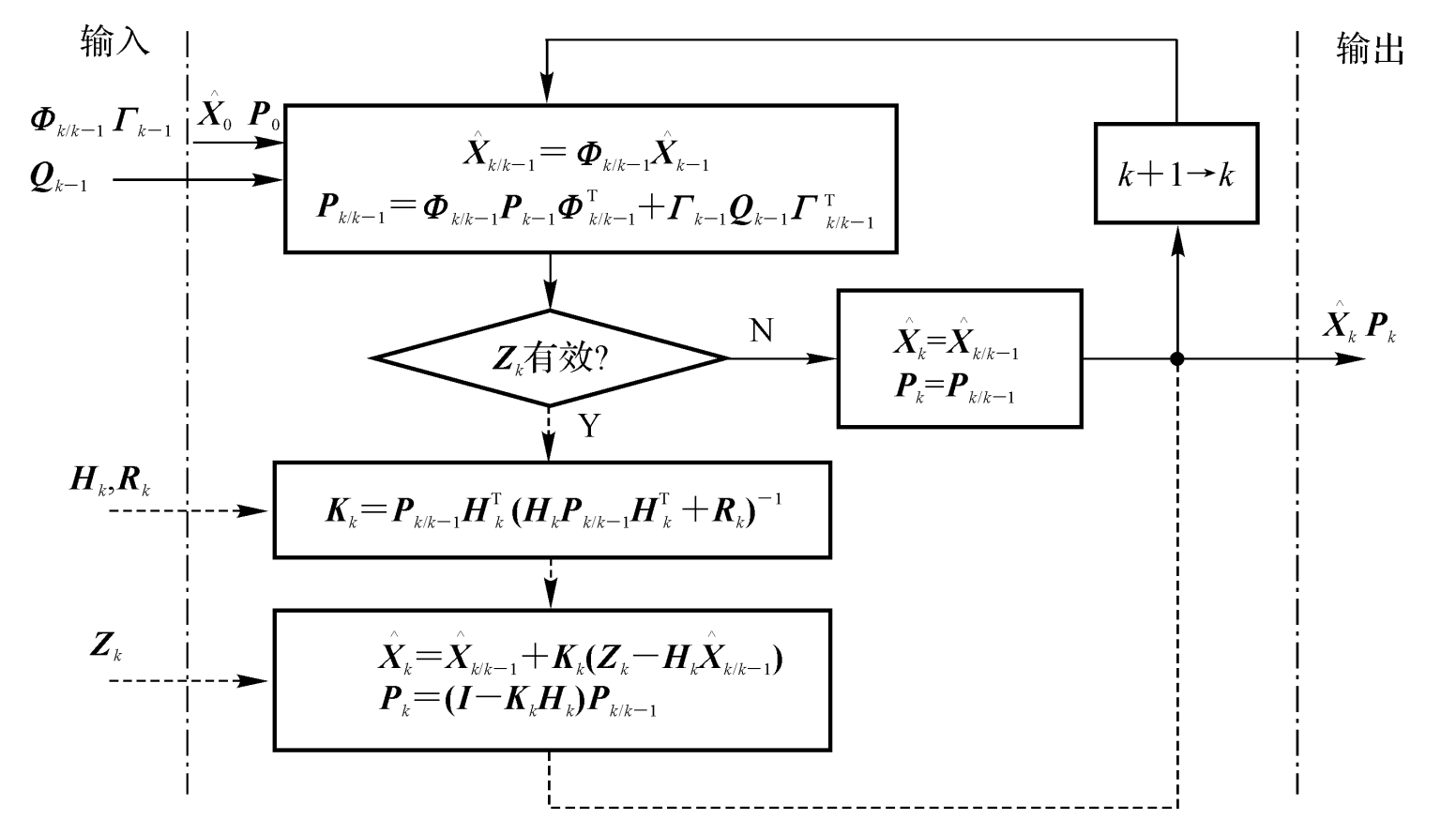
下面为卡尔曼滤波流程图

3. 从线性到非线性：EKF、UKF与IEKF

经典卡尔曼滤波只适用于线性系统。但现实中大部分系统都是非线性的，为此，出现了三种重要变体：

扩展卡尔曼滤波（EKF）：

EKF 通过在当前状态点附近对非线性函数进行局部线性化（泰勒展开），将非线性问题近似为线性问题。这种方法简单有效，但在非线性程度高的情况下，线性化误差会累积，导致性能下降甚至发散。
无迹卡尔曼滤波（UKF）：

UKF 放弃了线性化，而是采用无迹变换策略。它通过选择一系列能代表状态分布的**"Sigma点"**，将这些点直接通过非线性函数传播。这种方法能够更精确地捕捉非线性系统中的均值和协方差，通常在非线性程度较高时比 EKF 表现更好，并且避免了复杂的雅可比矩阵计算。
迭代扩展卡尔曼滤波（IEKF）：

IEKF 是 EKF 的一种改进版本，其核心思想是在更新步骤中进行多次迭代。在每次迭代中，IEKF 都根据最新的状态估计值重新计算雅可比矩阵和卡尔曼增益，并进行状态更新，直到估计值收敛。这种通过反复迭代逼近真实状态的方法，能显著减少单次线性化带来的误差，在观测模型高度非线性的问题中表现尤为出色。

每种方法的优缺点

卡尔曼滤波（KF）

KF 是所有卡尔曼滤波器的基础，它只适用于线性系统。

优点：在满足线性系统和高斯噪声假设的条件下，KF是最优的，能够得到最小均方误差的估计。它的实现简单，计算高效且稳定。
缺点：无法处理非线性系统。这是现实应用中的一个主要限制。

扩展卡尔曼滤波（EKF）

EKF 是 KF 最早、也是最著名的非线性扩展。它通过对非线性函数进行局部线性化来处理非线性问题。

优点：
- 实现相对简单：在理解 KF 的基础上，只需用雅可比矩阵替换状态和测量矩阵，算法结构保持不变。
- 计算高效：对于状态维度不高的系统，雅可比矩阵的计算通常比 UKF 的 Sigma 点传播更高效。
缺点：
- 精度有限 ：局部线性化引入了线性化误差，忽略了非线性带来的高阶项。在非线性程度较高时，精度会显著下降。
- 可能发散：当初始估计不准确或非线性太强时，线性化可能在不正确的点进行，导致滤波器发散。
- 需要计算雅可比矩阵：手动推导和实现复杂的雅可比矩阵既繁琐又容易出错。

无迹卡尔曼滤波（UKF）

UKF 放弃了线性化，采用无迹变换策略，通过确定性采样来处理非线性问题。

优点：
- 精度更高：UKF 能更准确地捕捉非线性变换，因此在处理高度非线性系统时，其精度通常优于 EKF。
- 鲁棒性更强：由于避免了线性化误差，UKF 拥有更好的数值稳定性和更低的发散风险。
- 无需雅可比矩阵：完全避免了雅可比矩阵的推导和计算，简化了实现过程。
缺点：
- 计算量较大：需要生成和传播一组 Sigma 点，当状态向量维度很大时，计算开销会显著增加。
- 理论上并非最优：尽管通常比 EKF 精确，但 UKF 也只是一个近似算法，其最优性不像 KF 那样严格。

迭代扩展卡尔曼滤波（IEKF）

IEKF 是 EKF 的一种改进版本，其核心思想是在更新步骤中进行多次迭代。它通过反复地将最新的状态估计值作为线性化点，来逼近更准确的估计。

优点：
- 显著减少线性化误差：通过反复迭代，每次都用更接近真实值的状态作为线性化点，可以有效减小单次线性化带来的误差。
- 精度高于标准 EKF：特别是在观测模型高度非线性的问题中，IEKF 通常比 EKF 表现更好，能更快速地收敛到准确的估计值。
缺点：
- 计算开销更大：需要在更新步骤中进行多次迭代，每次迭代都要重新计算雅可比矩阵和卡尔曼增益，这大大增加了计算量。
- 仍有发散风险：如果系统发散，迭代可能无法收敛到正确的值。

KF、EKF、UKF、IEKF 算法对比

特性/算法	卡尔曼滤波 (KF)	扩展卡尔曼滤波 (EKF)	无迹卡尔曼滤波 (UKF)	迭代扩展卡尔曼滤波 (IEKF)
系统类型	线性	非线性	非线性	非线性
处理非线性方式	不处理	局部线性化（泰勒展开）	无迹变换（确定性采样）	局部线性化（多次迭代）
雅可比矩阵	不需要	需要	不需要	需要
精度	最优（线性系统）	中等	高	高（优于 EKF）
计算量	低	中等	高（通常高于EKF）	高（通常高于EKF和UKF）
鲁棒性	高（稳定）	低（有发散风险）	高（比EKF稳定）	中等（比EKF稳定，但仍有发散风险）
典型应用	简单的线性系统	机器人定位、传感器融合	无人驾驶、精确导航	需要更高观测精度的非线性系统

扩充版：卡尔曼滤波详解

1. 引言：驾驭不确定性------卡尔曼滤波的革命性力量

在现代导航与定位技术领域，无论是指挥一架无人机精准穿越城市峡谷，还是助力自动驾驶汽车在毫秒间完成避障决策，核心挑战都源于对动态系统状态的实时、精确估计。然而，我们所处的物理世界充满了不确定性：传感器固有的噪声、系统模型的非线性、以及外部环境的未知扰动，都使得单一的数据源无法提供足够可靠的估计。正是在这样的背景下，卡尔曼滤波（Kalman Filter, KF）应运而生，成为融合多源信息、实现最优状态估计的基石性算法。

卡尔曼滤波的伟大之处在于，它以一种优雅的数学形式，解决了在不确定性环境下如何从带噪声的测量数据中提炼出系统真实状态的问题。它巧妙地将系统自身的动态模型预测与外部传感器的测量数据进行加权融合，从而生成一个比任何单一信息源都更精确、不确定性更小的最优估计。

2. 核心概念：预测、观测与最优融合

2.1 最优线性状态估计的基石：贝叶斯滤波

卡尔曼滤波在本质上是贝叶斯滤波（Bayesian Filter）在特定条件下的一个高效实现。贝叶斯滤波旨在通过递归地计算状态的后验概率分布来估计系统状态。它包含两个核心步骤：预测（Prediction）和更新（Update）。

卡尔曼滤波的"最优"性质，正是在系统是线性且所有噪声都服从高斯（正态）分布 这两个严格假设下所实现的。在高斯分布的假设下，任何状态分布都可以用其均值和协方差矩阵完全描述。卡尔曼滤波的递归公式正是对这两个二阶矩（均值和协方差）进行高效的传递与更新，从而在贝叶斯滤波的框架下实现了计算上的简洁与高效。

2.2 预测-更新循环：从不确定到最优的迭代

卡尔曼滤波的运行是一个持续的预测-更新循环。每一次迭代都包含以下两个主要阶段：

预测（Prediction）： 此阶段也被称为时间更新（Time Update），它利用已知的系统动态模型，根据上一时刻的最优状态估计和协方差，预测当前时刻的系统状态和不确定性。这个过程可以被视为一种"先验"估计，因为它是在尚未获得任何新的观测数据之前进行的。
更新（Update）： 此阶段也被称为测量更新（Measurement Update），当新的传感器观测值到来时，滤波器将预测值与观测值进行融合。通过引入观测信息，滤波器对先前的预测进行修正，从而得到一个更精确的、不确定性更小的当前时刻最优估计（"后验"估计）。

这种持续的递归迭代使得滤波器能够随着时间的推移，持续跟踪系统的真实状态并减小估计误差。

2.3 核心思想的精髓：卡尔曼增益（Kalman Gain）

卡尔曼增益（ K k K_k Kk）是卡尔曼滤波算法中最为关键的参数之一。它是一个权重系数 ，决定了在更新步骤中，我们应该相信预测结果多一点，还是相信传感器观测值多一点。卡尔曼增益并非凭空设定，其数学推导是通过最小化后验估计误差的协方差（即均方误差）得到的。

从物理直觉上看，卡尔曼增益是一种理性的决策模型。其大小直接反映了模型预测的不确定性 与传感器观测的不确定性 之间的相对关系。当预测状态的不确定性（协方差 P P P）很大，而传感器观测的不确定性（噪声协方差 R R R）很小时，增益 K K K 会变大，这意味着算法会更多地采纳观测值来修正预测，因为此时传感器信息更为可靠。反之，当模型预测非常精确，而传感器噪声很大时，增益 K K K 会变小，算法会更多地依赖预测结果，而对观测值的修正作用较小。这种对"信任"的量化与动态调整，是卡尔曼滤波能够在不确定性系统中实现最优估计的深层原因。

3. 五大核心公式的数学推导与物理直觉

卡尔曼滤波的递归过程由五大核心方程构成，可以分为预测和更新两大步骤。

3.1 预测步骤

在预测步骤中，滤波器利用已知的系统模型来预测下一时刻的状态和不确定性。

状态预测方程：
x ^ k ∣ k − 1 = F k x ^ k − 1 ∣ k − 1 + B k u k − 1 \hat{x}{k|k-1} = F_k \hat{x}{k-1|k-1} + B_k u_{k-1} x^k∣k−1=Fkx^k−1∣k−1+Bkuk−1
- x ^ k ∣ k − 1 \hat{x}_{k|k-1} x^k∣k−1。 k k k 时刻的先验状态估计（预测值）。
- x ^ k − 1 ∣ k − 1 \hat{x}_{k-1|k-1} x^k−1∣k−1。 k − 1 k-1 k−1 时刻的后验状态估计（最优估计）。
- F k F_k Fk。状态转移矩阵，描述系统状态如何从 k − 1 k-1 k−1 转移到 k k k。
- u k − 1 u_{k-1} uk−1。 k − 1 k-1 k−1 时刻的控制输入向量。
- B k B_k Bk。控制输入矩阵。
协方差预测方程：
P k ∣ k − 1 = F k P k − 1 ∣ k − 1 F k T + Q k P_{k|k-1} = F_k P_{k-1|k-1} F_k^T + Q_k Pk∣k−1=FkPk−1∣k−1FkT+Qk
- P k ∣ k − 1 P_{k|k-1} Pk∣k−1。 k k k 时刻的先验协方差矩阵。
- P k − 1 ∣ k − 1 P_{k-1|k-1} Pk−1∣k−1。 k − 1 k-1 k−1 时刻的后验协方差矩阵。
- Q k Q_k Qk。过程噪声协方差矩阵，代表系统动态模型本身的不确定性。

从协方差预测方程可以看出，即使没有控制输入和外部扰动，不确定性（协方差）也会在预测过程中增大。这是因为过程噪声协方差矩阵 Q k Q_k Qk 的引入。 Q k Q_k Qk 矩阵表征了我们对系统动态模型的不信任度，它代表了模型简化、未知的外部干扰或系统本身固有的随机性。因此，预测过程总会增加不确定性，使得预测后的协方差 P k ∣ k − 1 P_{k|k-1} Pk∣k−1 通常大于 P k − 1 ∣ k − 1 P_{k-1|k-1} Pk−1∣k−1。

3.2 更新步骤

当传感器提供新的观测数据后，滤波器进入更新步骤，利用观测信息修正预测结果。

卡尔曼增益方程：
K k = P k ∣ k − 1 H k T ( H k P k ∣ k − 1 H k T + R k ) − 1 K_k = P_{k|k-1} H_k^T (H_k P_{k|k-1} H_k^T + R_k)^{-1} Kk=Pk∣k−1HkT(HkPk∣k−1HkT+Rk)−1
- K k K_k Kk：卡尔曼增益。
- H k H_k Hk：观测矩阵，将状态向量映射到观测向量。
- R k R_k Rk：观测噪声协方差矩阵，代表传感器观测值的不确定性。

该方程通过权衡先验协方差 P k ∣ k − 1 P_{k|k-1} Pk∣k−1 和观测噪声 R k R_k Rk 来计算增益。

状态更新方程：
x ^ k ∣ k = x ^ k ∣ k − 1 + K k ( z k − H k x ^ k ∣ k − 1 ) \hat{x}{k|k} = \hat{x}{k|k-1} + K_k(z_k - H_k \hat{x}_{k|k-1}) x^k∣k=x^k∣k−1+Kk(zk−Hkx^k∣k−1)
- x ^ k ∣ k \hat{x}_{k|k} x^k∣k： k k k 时刻的后验状态估计（最优估计）。
- z k z_k zk： k k k 时刻的传感器观测值。
- ( z k − H k x ^ k ∣ k − 1 ) (z_k - H_k \hat{x}_{k|k-1}) (zk−Hkx^k∣k−1)：这一项被称为"新息"（Innovation）或"测量残差"，它反映了实际观测值与预测观测值之间的差异。滤波器利用卡尔曼增益对这一差异进行加权，然后将其添加到先验状态中进行修正。
协方差更新方程：
P k ∣ k = ( I − K k H k ) P k ∣ k − 1 P_{k|k} = (I - K_k H_k)P_{k|k-1} Pk∣k=(I−KkHk)Pk∣k−1
- P k ∣ k P_{k|k} Pk∣k： k k k 时刻的后验协方差矩阵。
- I I I：单位矩阵。

由于引入了新的观测信息，我们的不确定性会减小。该方程表明，通过将卡尔曼增益与先验协方差相乘并从先验协方差中减去，新的后验协方差 P k ∣ k P_{k|k} Pk∣k 将比预测的 P k ∣ k − 1 P_{k|k-1} Pk∣k−1 更小，这物理上代表了估计不确定性的降低。

下面为卡尔曼滤波流程图

4. 从线性到非线性：EKF、UKF与IEKF

4.1 扩展卡尔曼滤波（EKF）：非线性系统的线性化之道

经典卡尔曼滤波严格适用于线性系统。但在现实世界中，许多系统的运动模型或观测模型都是非线性的。扩展卡尔曼滤波（EKF）正是为了解决这一问题而设计的。

EKF 的核心思想是通过对非线性函数进行局部线性化 来近似处理非线性。具体而言，它在当前的状态估计点附近，对非线性的状态转移函数 f ( x ) f(x) f(x) 和观测函数 h ( x ) h(x) h(x) 进行一阶泰勒级数展开 ，然后忽略高阶项，将其近似为线性函数。在这个近似过程中，卡尔曼滤波中的状态转移矩阵 F F F 和观测矩阵 H H H 被非线性函数的雅可比矩阵所取代。这些雅可比矩阵需要在每一个滤波周期实时计算，并根据最新的状态估计值来确定。

然而，EKF的局限性源于其核心假设：泰勒展开仅是局部线性近似。如果系统的高度非线性，或者状态估计误差较大，这种近似误差可能会显著累积，导致滤波器性能下降甚至发散。这是 EKF 的根本缺陷，也是后续更高级算法诞生的原因。

4.2 无迹卡尔曼滤波（UKF）：无迹变换的优雅

为了克服 EKF 的线性化误差，无迹卡尔曼滤波（UKF）应运而生。UKF 不进行线性化，而是采用一种称为无迹变换（Unscented Transform）的策略。

其核心思想是：通过选择一系列特定的"Sigma点"（一个精心挑选的点集，代表状态分布的均值和协方差），然后将这些点直接通过非线性函数进行传播，最后根据传播后的点集重新计算新的均值和协方差。这种方法能够更精确地捕捉高斯随机变量通过非线性变换后的均值和协方差，而无需计算复杂的雅可比矩阵。因此，UKF 的优点在于不引入线性化误差，通常在非线性程度较高时比 EKF 表现更优，并且避免了复杂的雅可比矩阵计算，简化了建模过程。

4.3 迭代扩展卡尔曼滤波（IEKF）：精益求精的迭代

迭代扩展卡尔曼滤波（IEKF）是 EKF 的一种改进版本，旨在进一步减小线性化误差。IEKF 的核心思想是在每次更新步骤中进行多次迭代。在每一次迭代中，它都根据当前的最新状态估计值重新计算雅可比矩阵和卡尔曼增益，并进行状态更新，直到状态估计收敛到稳定值。这种通过反复迭代来逼近真实状态的方法，可以显著减少因单次线性化带来的误差，尤其是在观测模型高度非线性的问题中，它能提供比 EKF 更精确的估计，并且不容易发散。

不同算法的优劣对比

卡尔曼滤波 (KF)

卡尔曼滤波 是所有卡尔曼滤波器的基础，专为线性系统 设计。它是一个最优线性估计器 ，意味着在满足特定假设（系统线性、噪声高斯）的前提下，它能得到最小均方误差的估计。

工作原理 ：KF 遵循一个简单的"预测-更新 "循环。它首先根据一个已知的线性模型来预测下一时刻的状态，这个预测会带有不确定性。接着，它利用新的传感器测量值 来更新这个预测，通过智能地融合预测和测量信息来得到一个更精确的估计。

优点：
- 最优性：在理想条件下，没有比它更好的线性估计方法。
- 高效稳定：算法结构简单，计算量小，且数值稳定。
缺点：
- 限制性强：仅适用于线性系统。现实中的大多数系统（如无人机、机器人等）都是非线性的，这大大限制了其直接应用。

扩展卡尔曼滤波 (EKF)

扩展卡尔曼滤波 是卡尔曼滤波处理非线性系统 的最早且最广泛使用的方法。它的核心思想是：将非线性问题近似为线性问题。

工作原理 ：EKF 在每一步都对非线性函数（状态转移函数和测量函数）在当前估计点附近进行一阶泰勒展开，从而得到一个线性近似。随后，它像标准卡尔曼滤波一样，利用这些线性化后的矩阵进行预测和更新。

优点：
- 实现简单 ：在 KF 的基础上，只需用雅可比矩阵（非线性函数的一阶偏导数矩阵）来代替原来的线性矩阵，算法结构几乎不变。
- 计算高效：如果系统雅可比矩阵可以解析求解，其计算量相对较低，对于许多准线性系统来说，足以满足实时性要求。
缺点：
- 精度受限 ：泰勒展开只保留了一阶项，忽略了高阶项，导致线性化误差。当系统非线性程度很高时，这个误差会累积，导致估计精度显著下降。
- 可能发散 ：由于线性化误差，如果滤波器的初始估计不准确，或者系统动态变化剧烈，EKF 可能会偏离真实轨迹并发散。
- 需要计算雅可比矩阵：手动推导和实现复杂的雅可比矩阵是一项繁琐且容易出错的工作。

无迹卡尔曼滤波 (UKF)

无迹卡尔曼滤波 是一种更先进的非线性滤波方法，旨在克服 EKF 的主要缺点。它放弃了线性化 ，转而采用一种更聪明的确定性采样策略。

工作原理 ：UKF 不去近似非线性函数，而是直接近似高斯分布 。它在当前状态的估计点周围，精心选取一组被称为 Sigma 点的采样点。这些点能够精确地捕捉状态的均值和协方差。然后，UKF 将这些 Sigma 点直接通过完整的非线性函数进行传播，再根据新的 Sigma 点集合重新计算预测的均值和协方差。

优点：
- 精度更高：UKF 能够更准确地捕捉非线性带来的影响，因此在处理强非线性系统时，其估计精度通常远优于 EKF。
- 鲁棒性强：由于没有线性化误差，UKF 的数值稳定性更好，发散的风险也大大降低。
- 无需雅可比矩阵：UKF 完全避免了复杂的雅可比矩阵计算，简化了实现过程。
缺点：
- 计算量较大 ：需要生成并传播 2 n + 1 2n+1 2n+1 个 Sigma 点（ n n n 为状态维度），这会增加计算负担，尤其是在高维系统中。

迭代扩展卡尔曼滤波 (IEKF)

迭代扩展卡尔曼滤波 是 EKF 的一种改进版，旨在提高其在观测模型高度非线性时的精度。它保留了 EKF 的核心思想，但在更新步骤中增加了多次迭代。

工作原理 ：在更新阶段，IEKF 不仅进行一次更新，而是反复进行。它首先像 EKF 一样进行一次更新，然后将新得到的估计值作为下一次迭代的线性化点，重新计算雅可比矩阵和卡尔曼增益，并再次更新。这个过程会重复多次，直到估计值收敛到稳定点。

优点：
- 精度更高：通过在更接近真实值的点进行线性化，IEKF 能够显著减小线性化误差，在观测高度非线性的问题中表现尤为出色。
- 收敛速度快：在理想情况下，迭代能使估计值快速逼近最优解。
缺点：
- 计算量大：每次迭代都需要重新计算雅可比矩阵和卡尔曼增益，这大大增加了计算负担，可能影响实时性。
- 收敛问题：如果系统存在发散问题，迭代可能无法收敛到正确的值，甚至加剧发散。

综合对比表格

特性/算法	卡尔曼滤波 (KF)	扩展卡尔曼滤波 (EKF)	无迹卡尔曼滤波 (UKF)	迭代扩展卡尔曼滤波 (IEKF)
系统类型	线性	非线性	非线性	非线性
处理非线性方式	不处理	局部线性化	无迹变换	多次迭代线性化
核心操作	线性代数	矩阵求导（雅可比）	确定性采样	矩阵求导与迭代
雅可比矩阵	不需要	需要	不需要	需要
精度	最优（线性系统）	中等（受线性化误差影响）	高（通常优于EKF）	高（优于EKF，与UKF各有所长）
鲁棒性	高（稳定）	低（有发散风险）	高（比EKF稳定）	中等（比EKF稳定，但有收敛风险）
计算量	低	中等	较高	高
适用场景	线性导航、简单追踪	机器人定位、传感器融合	高精度导航、状态估计	观测模型高度非线性且计算资源允许的场景