一、概念
**矩阵:**由数字组成的矩形阵列,并写咋方括号内。
**矩阵的维度:**矩阵的行数乘以列数
**向量:**是一种特殊的矩阵,是只有一列的矩阵(N*1)。
二、矩阵的计算
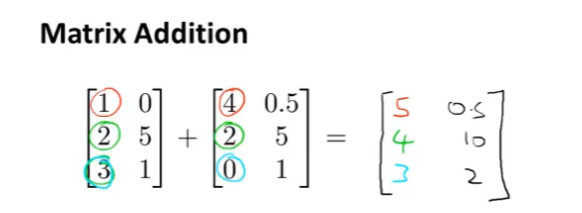
矩阵的加法:只有两个相同维度的两个矩阵才能相加
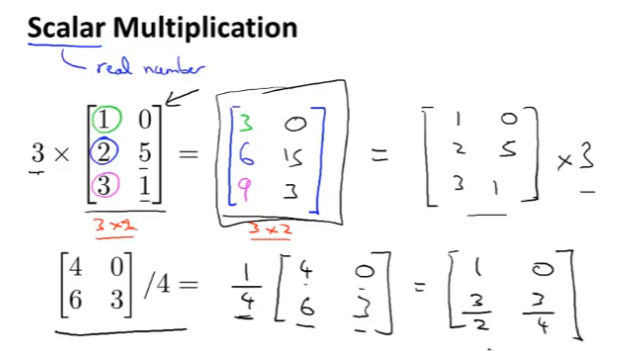
矩阵的标量乘法:
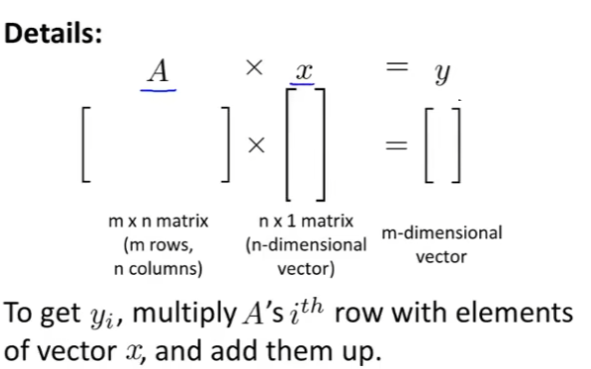
矩阵向量的乘法:矩阵的列数量等于向量的行的数量
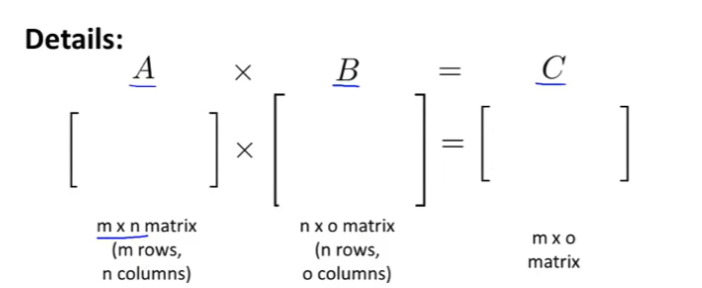
矩阵乘法:不符合交换定律
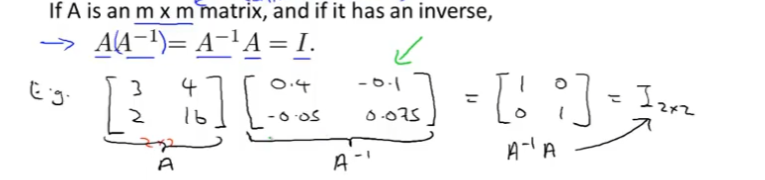
矩阵的逆:
矩阵的转置:
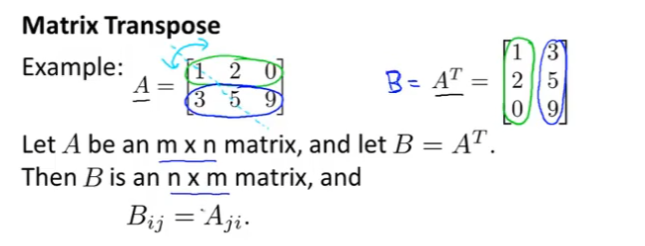
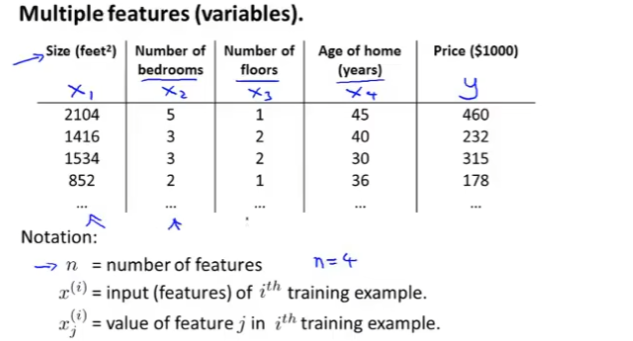
二、多元线性回归
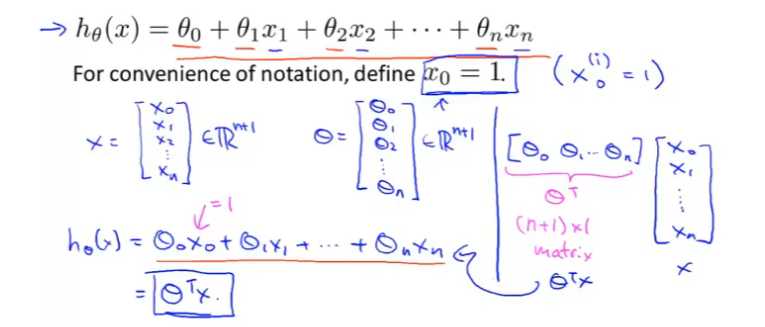
多元梯度下降法:

这里的是一个向量。

特征缩放:标准化与归一化


**学习率:**控制模型参数更新步长的超参数
学习率取值的两种情况:
**① 学习率过大:**参数更新步长过大,可能导致损失值震荡甚至发散。
**② 学习率过小:**收敛速度极慢,可能陷入局部极小值。
正规方程:单独加一列x0,其值永远为1.
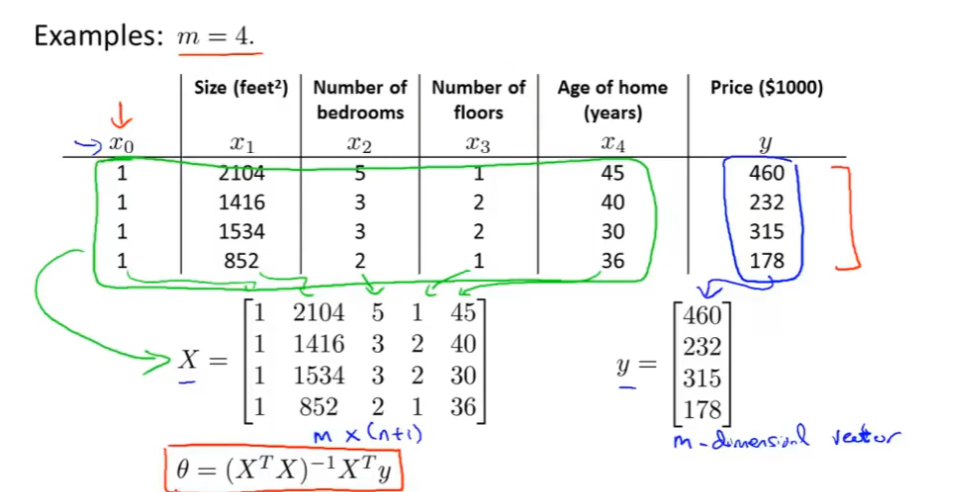
正规方程与梯度下降的区别:
