双指针算法
移动零
题目分析 :给我们一个数组,我们将其所有0元素在右边,非0元素在边,并且原本的非0元素的相对顺序不变
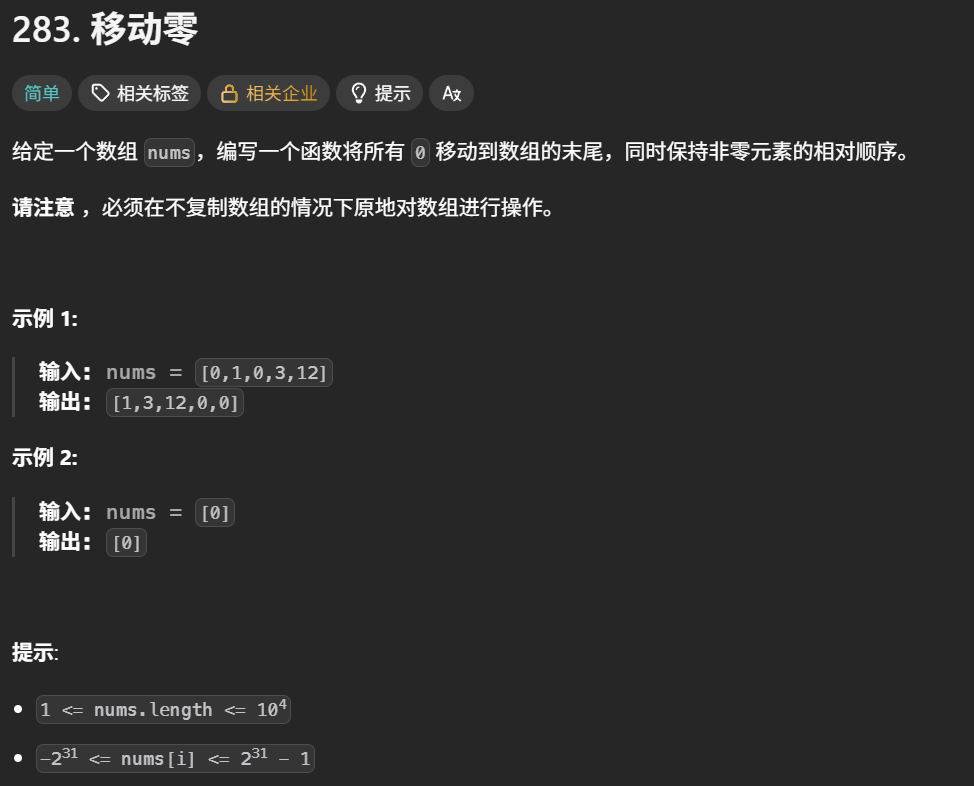
算法原理 :我们可以将这个数组分块,这里我们通常使用双指针算法我们这里的数组中的双指针,使用其来表示下标,因为对应下标就有对应的值
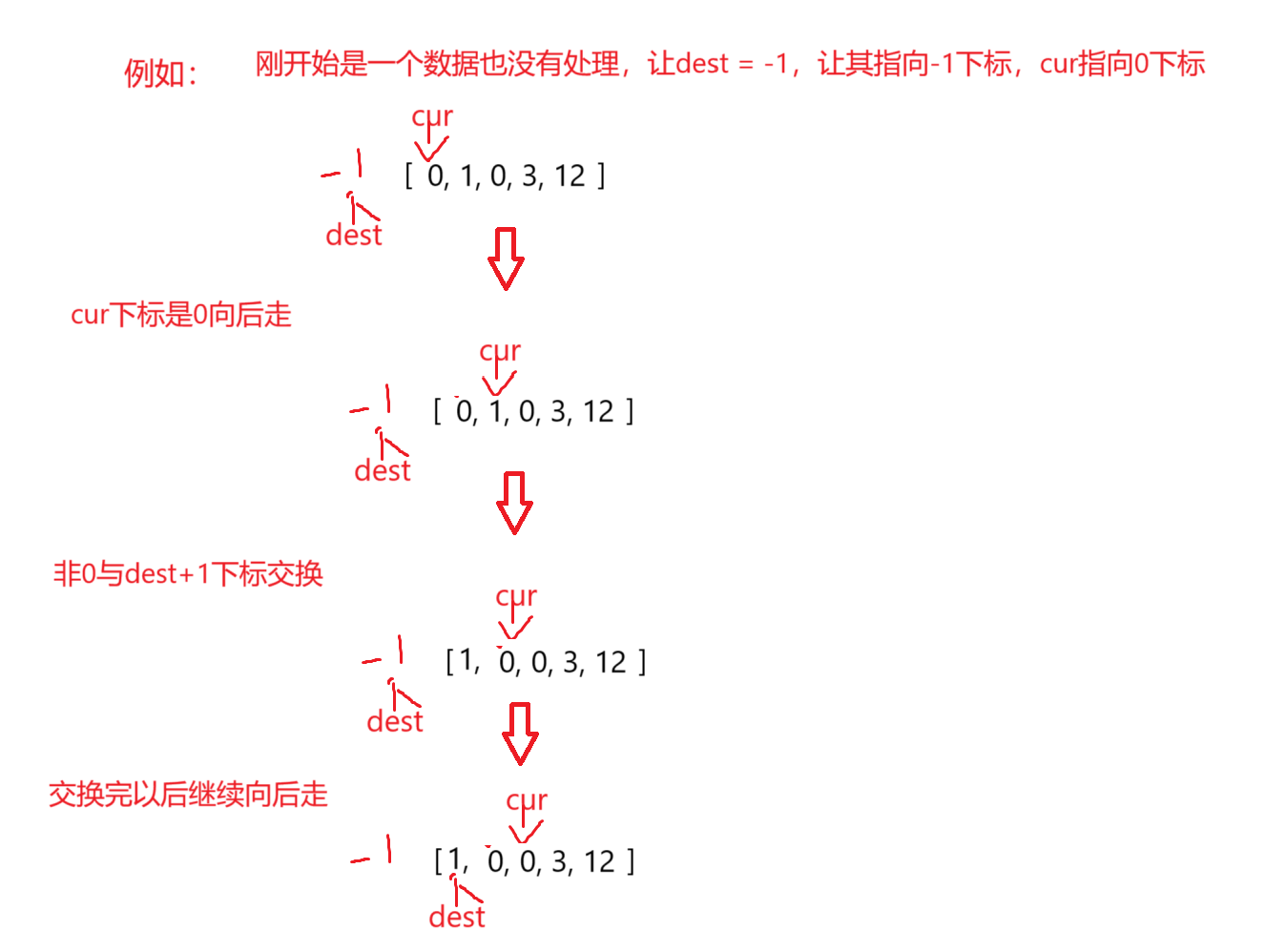
我们在不断的调整的时候,数组可以分为已调整和未调整区间 ,已调整区间又有0区间和非0区间 ,如何调整呢,这时候就用dest和cur指针
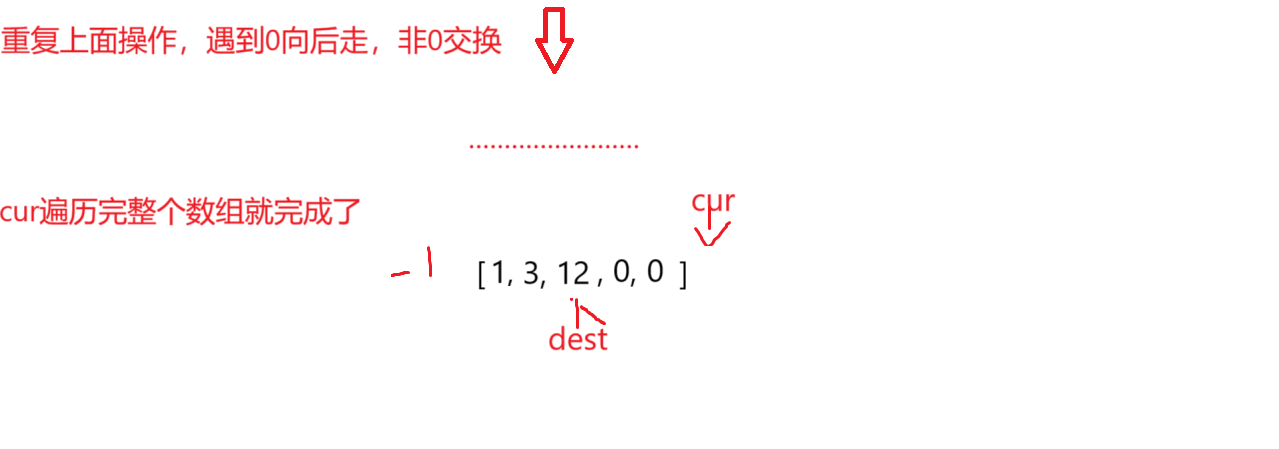
cur遍历这个数组,dest下标对应的是已调整区间最后一个非0元素就这样让cur遍历,遇到0元素继续向后走,遇到非0元素,与前面已调整的第一个0元素进行交换,就这样一直操作,左侧就会变成非0元素,右侧就会变成0元素

java
class Solution {
public void moveZeroes(int[] nums) {
int dest = -1;//表示已处理的非零和零之间的最后一个非零元素下标
for(int cur = 0;cur<nums.length;cur++){
if(nums[cur] != 0){
dest++;
int tem = nums[dest];
nums[dest] = nums[cur];
nums[cur] = tem;
}
}
}
}时间复杂度:O(N),空间复杂度:O(1)
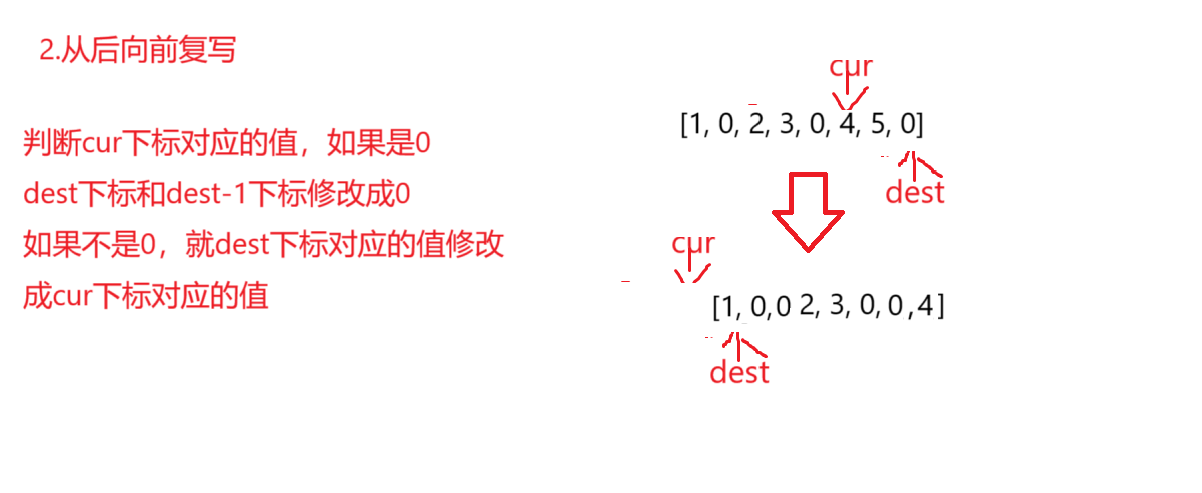
复写零

题目分析 :就是出现的每个零都复写一遍,并将其余的元素向右平移,但是数组总长度不变并且要就地进行修改
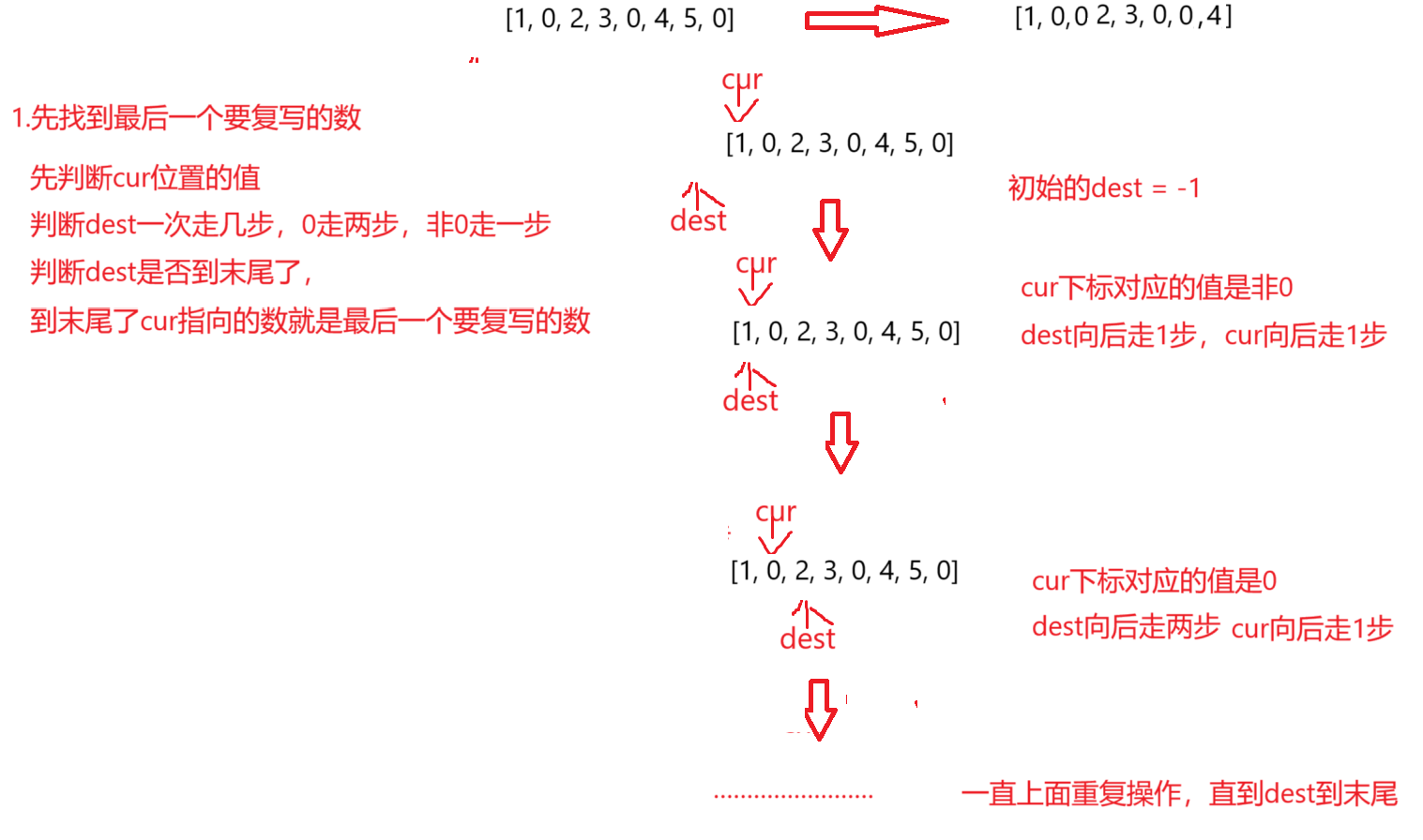
算法原理 :使用双指针 1.先找到最后一个要复写的数2.从后向前复写因为我们如果直接从前向后复写的话,这里复写过程中会影响到后面没有被复写过的数,这样结果就不对了

sql
class Solution {
public void duplicateZeros(int[] arr) {
//1.先找到最后一个要复习的数
int cur = 0;
int dest = -1;
int n = arr.length;
while(cur<n){
if(arr[cur] == 0){
dest+=2;
}else{
dest++;
}
//到末尾了,此时cur下标对应的值就是最后一个要复写的值
if(dest>=n-1){
break;
}
cur++;
}
//2.判断边界
if(dest>=n){
arr[n-1] = 0;
dest -= 2;
cur--;
}
//3.从后向前复写
while(cur>=0){
if(arr[cur] == 0){
arr[dest--] = 0;
arr[dest--] = 0;
cur--;
}else{
arr[dest--] = arr[cur--];
}
}
}
}时间复杂度:O(N),空间复杂度:O(1)
快乐数

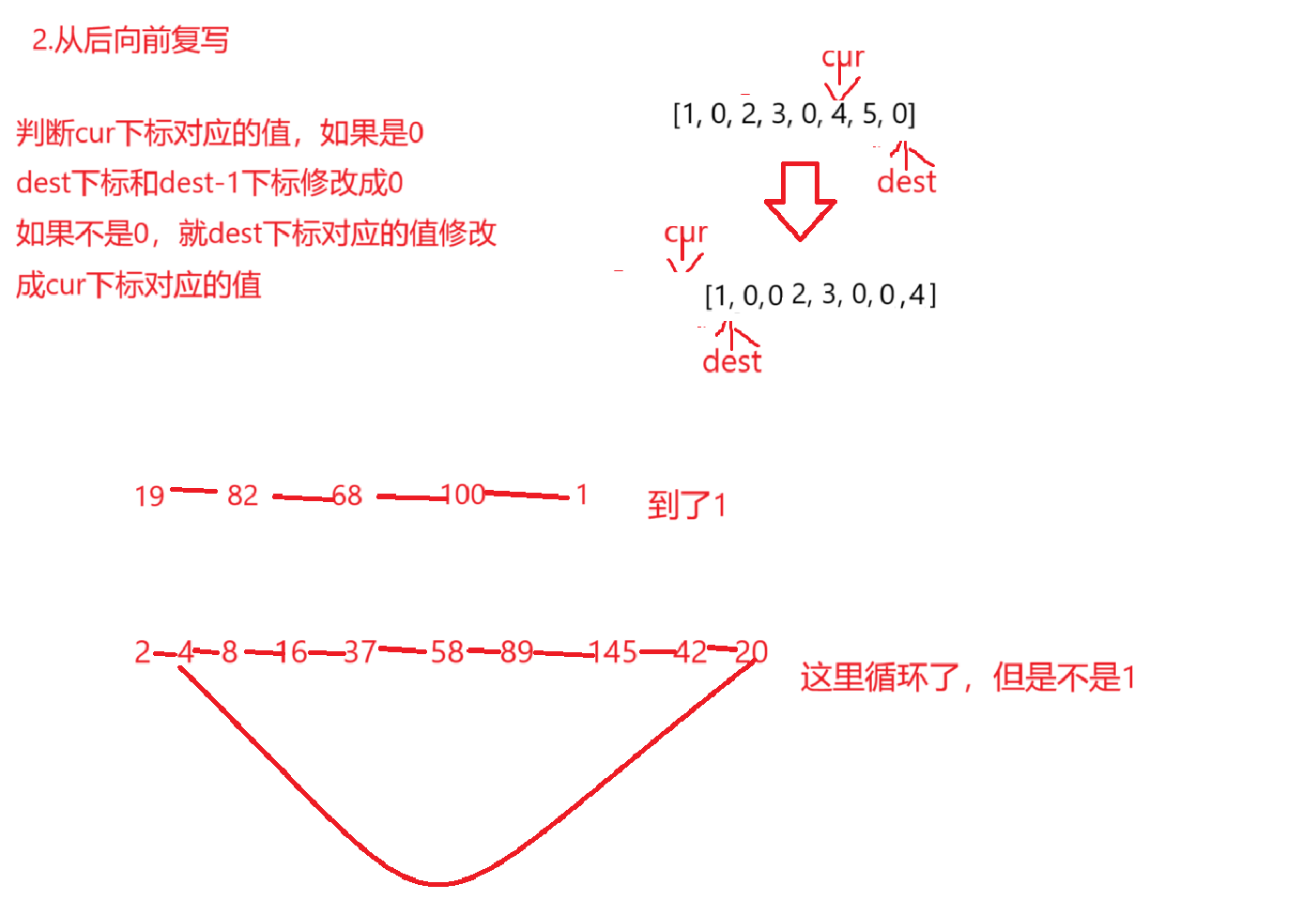
题目解析 :一个数不断的变成其每个位置的平方和,如果这个平方和循环到1就是快乐数,反之就不是快乐数
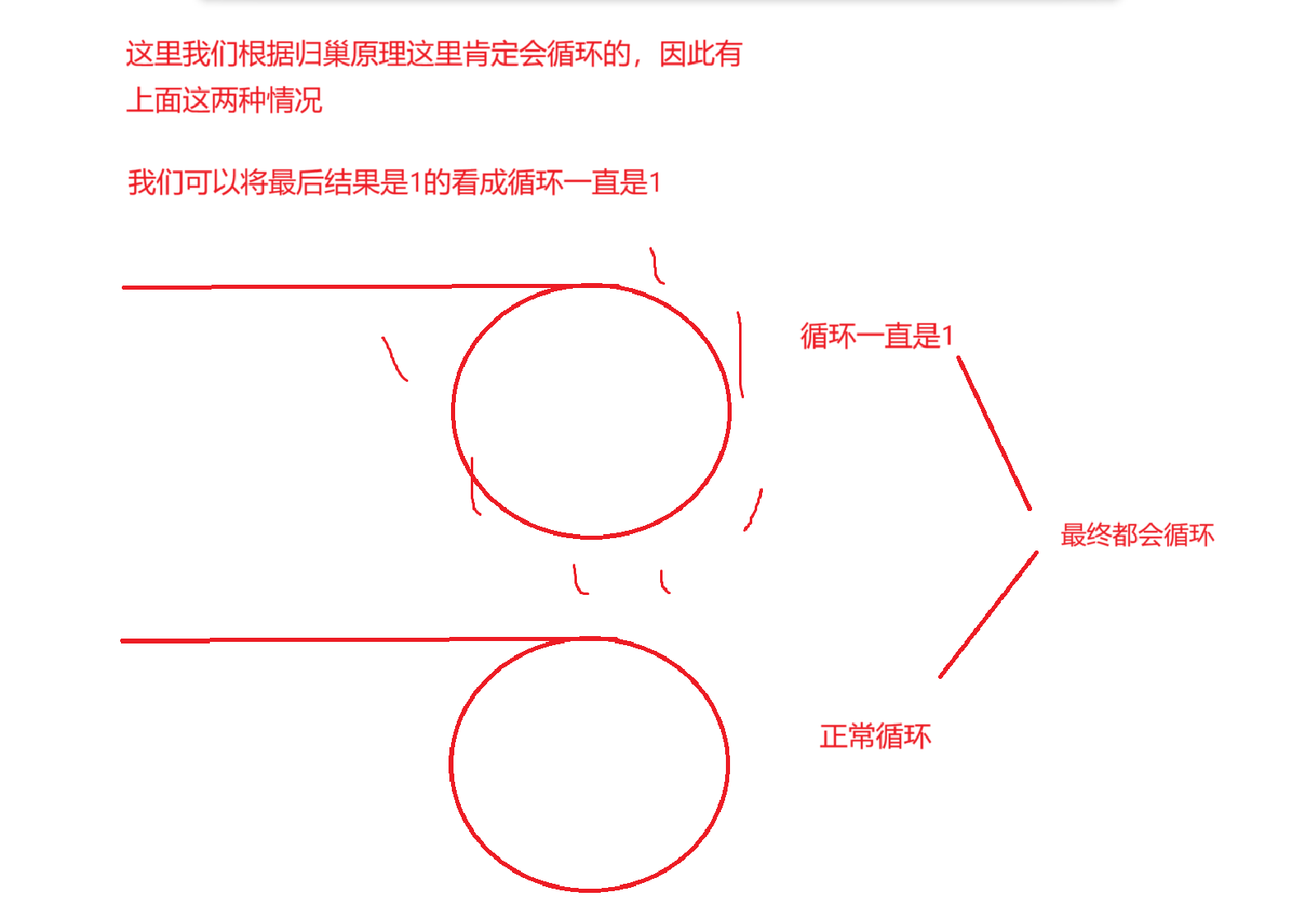
算法原理 :双指针算法,这里循环到1其实可以看成其后面一直循环,但循环的值一直是1,这样就有这两种情况,和以前判断链表是否有环一样,快慢指针,他们有环的话终究会相遇的 ,最后判断相遇的位置是否是1就行,这里无论怎样都会有循环,因为这里的n的范围是有限制的,根据归巢原理可知
快慢指针,slow和fast,slow一次走一步,fast一次走两步,直到相遇
java
class Solution {
public boolean isHappy(int n) {
int slow = n;
//由于这里是slow==fast结束,所以刚开始先让fast先走两步
int fast = bitSum(bitSum(n));
while(slow != fast){
slow = bitSum(slow);
fast = bitSum(bitSum(fast));
}
return slow == 1;
}
//用来求每一位平方和
public int bitSum(int n){
int sum = 0;
while(n != 0){
int tem = n % 10;
sum += tem*tem;
n /= 10;
}
return sum;
}
}时间复杂度 O(log n) ,空间复杂度 O(1)
盛最多水的容器
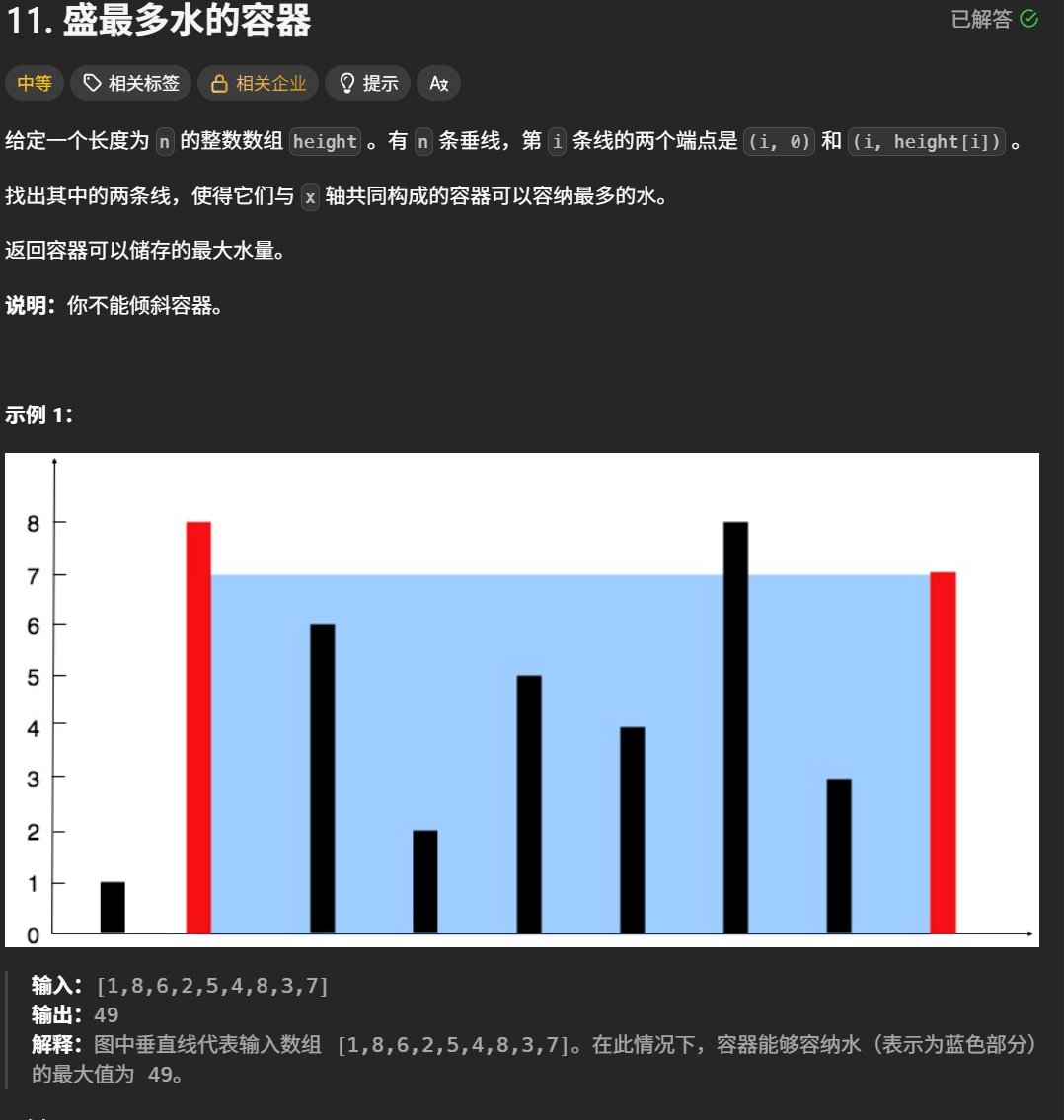
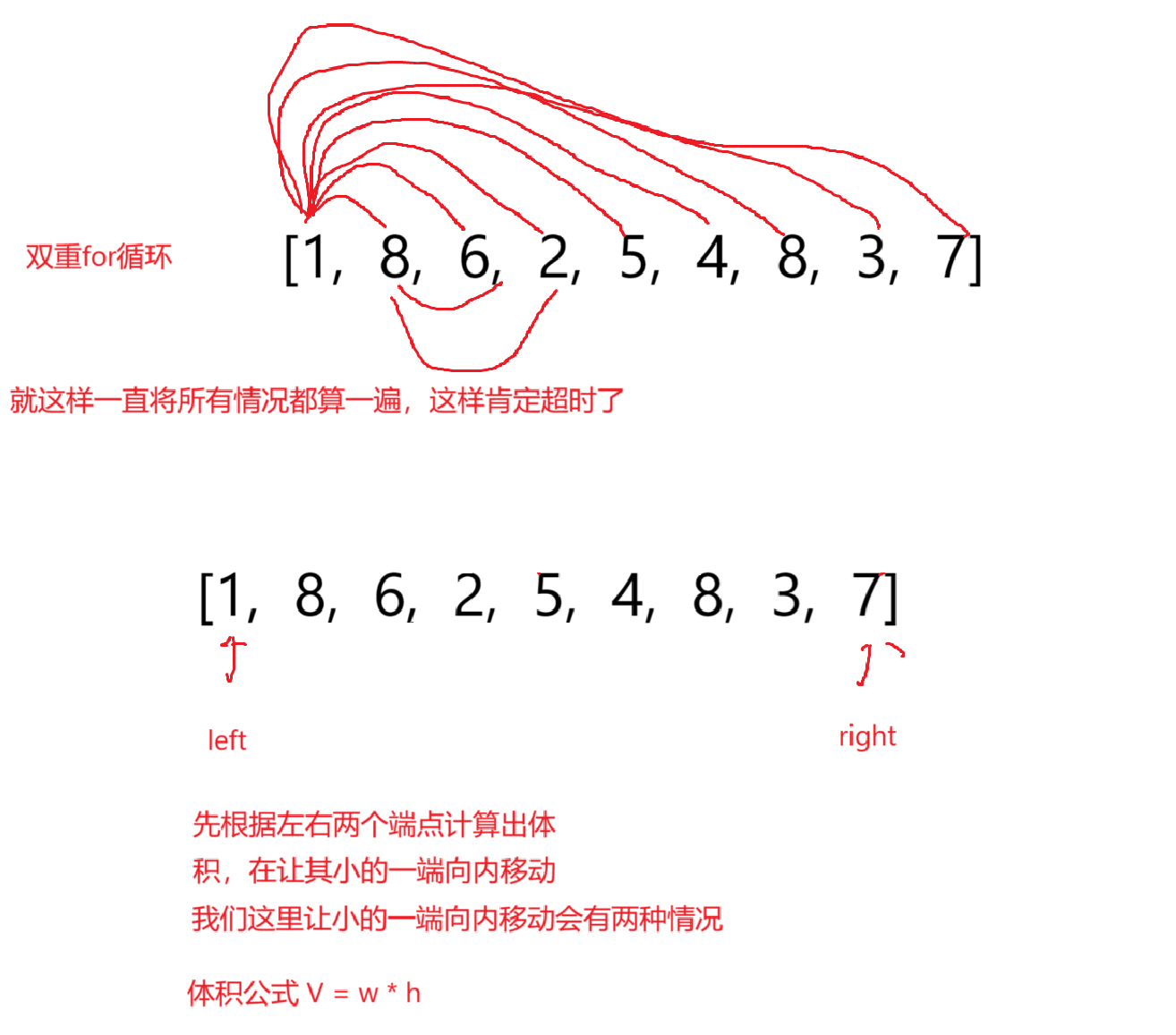
题目解析:这里就是给我们好多的垂线,让我们求出那两根放一起是体积最大,首先我们就是想到的是双重for循环将所有情况全部枚举出来这样,结果是正确的,但是时间超时了
算法原理:双指针算法,left数组的左端,right数组的右边,一直根据左右来计算出体积,让小的一段向内移动,继续计算体积,重复操作,最终就可以求出最大体积


java
class Solution {
public int maxArea(int[] height) {
//一直根据两端来求一个体积
//让其短的一边向内移动,直到两个相遇
int left = 0;
int right = height.length - 1;
int max = 0;//最大的体积
while(left != right){
//木桶效应,高是最低的那个
int V = Math.min(height[left],height[right]) * (right - left);
if(V > max){
max = V;
}
//向内移动
if(height[left] > height[right]){
right--;
}else{
left++;
}
}
return max;
}
}时间复杂度:O(N),空间复杂度:O(1)
有效三角形的个数
题目解析 :在一个数组中找三个数,有多少种情况是满足三角形:两边之和大于第三边
算法原理 :首先我们想到的是暴力解法,就是三层for循环,这样时间复杂度是N^3,这样肯定超时了,不满足题目要求1.这里我们发现每次判断是不是三角形都要比较三次 ,这样也导致其时间复杂度变成3N^3,所以这里我们要知道一个只是,就是比如 a <= b<= c判断这三条边是否可以构成三角形,其实只需要判断其a+b>c这一个条件就行剩下的两个已经满足,此时时间复杂度变成了N logN+N ^ 2
2.这时候可以先将数组按升序排列,使用双指针算法,首先每次从最右边确定一个最大的数,剩下俩个数从前面确定这时候就有left和right这两个,如果满足nums[left] + nums[right] > 最大的数,并且在其左边还是一次递减,说明这里区间都满足,让其加上 right - left,right-- 反之左边left++,就这样一直到其最大的数下标到2就说明结束了


sql
class Solution {
public int triangleNumber(int[] nums) {
//1.先进行排序,这样判断三角形只需要判断一次
Arrays.sort(nums);
int count = 0;
for (int i = nums.length - 1; i >= 2; i--) {
//2.双指针算法
int left = 0;
int right = i - 1;
while (left<right) {
//剩下的两个数从前向后找
if (nums[left] + nums[right] > nums[i]) {
//这里如果大于最大的数,说明这个区间的左边与右边这个数都满足三角形
//left向右都满足
count += (right - left);
right--;
} else {
//不满足的话,right向左肯定都不满足
left++;
}
}
}
return count;
}
}时间复杂度O(N^2),空间复杂度:O(1)
两数之和
题目解析 :就是给我们一个有序的数组,和一个目标数target,并且有且只有一个,返回这两个下标,注意:这里的数组是升序排列的
算法原理:1.我们首先想到的就是暴力解法:双重for循环 找到其俩个下标返回,但是这个时间复杂度高,并且没有用到其数组是升序排列 这个条件
2.双指针算法:就是先定义两个指针left指向数组最左边,right指向数组最右边,这样我们让其对应的值相加与target目标值相比,如果>target就说明大了,就让right--,如果<target说明小了,就让left++,反之就找到了


java
class Solution {
public int[] twoSum(int[] numbers, int target) {
//1.双指针left和right
int left = 0;
int right = numbers.length - 1;
while(left<right){
if(numbers[left]+numbers[right] > target){
right--;
}else if(numbers[left] + numbers[right] < target){
left++;
}else{
return new int[]{left,right};
}
}
return new int[]{0};
}
}时间复杂度:O(N),空间复杂度:O(1)
三数之和
题目分析 :就是在数组中找出所有的三元组,并且这个三元组之和为0,并且不可以重复
算法原理 :1.暴力枚举:这里首先就是可以暴力解法,就是三重for循环进行判断,这里可以使用set进行去重,或者自己编写代码去重,但是这种肯定时间复杂度超出了要求2.双指针算法:由于原本的数组是无序的,所以我们找出结果也是无序的进行去重的时候是不容易去重,因此我们这里是先排序,在进行使用双指针去找,数组从后向前遍历,先确定一个最大的数,剩下两个数在其前面用双指针去找满足三数之和为0的三元组并去重




java
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> ret = new ArrayList<>();
Arrays.sort(nums);
int n = nums.length;
for (int i = 0; i < n; ) {
//双指针都在其右边,如果其>0那肯定不满足了
if (nums[i] > 0) {
break;
}
int left = i + 1;
int right = n - 1;
int target = -nums[i];
while (left < right) {
int sum = nums[left] + nums[right];
if(sum>target){
right--;
}else if(sum<target){
left++;
}else{
List<Integer> list = new ArrayList<>();
list.add(nums[i]);
list.add(nums[left]);
list.add(nums[right]);
ret.add(list);
left++;
right--;
while(left<right&&nums[left] == nums[left-1]){
left++;
}
while(left<right&&nums[right] == nums[right+1]){
right--;
}
}
}
//这里对i进行去重
i++;
while(i<n&&nums[i] == nums[i-1]){
i++;
}
}
return ret;
}
}时间复杂度(O(N^2+ N * log N) ,空间复杂度:O(1)
四数之和

这里的四数之和其实和上面的三数之和一样的,只不过上面我们只是先确定一个数,这里我们就先确定两个数,并且都要注意去重处理
并且这里会出现int相加超过了其最大范围,所以这里我们要强制类型转换为long
java
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> ret = new ArrayList<>();
//1.先排序
Arrays.sort(nums);
int n = nums.length;
for (int i = 0; i < n;) {
for (int j = i + 1; j < n;) {
int left = j + 1;
int right = n - 1;
long Newtarget = (long)target - nums[i] - nums[j];
while (left < right) {
int sum = nums[left] + nums[right];
if (sum > Newtarget) {
right--;
} else if (sum < Newtarget) {
left++;
} else {
List list = new ArrayList<>();
list.add(nums[i]);
list.add(nums[j]);
list.add(nums[left]);
list.add(nums[right]);
ret.add(list);
left++;
right--;
//这里要注意去重
while (left < right && nums[left] == nums[left - 1]) {
left++;
}
while (left < right && nums[right] == nums[right + 1]) {
right--;
}
}
}
j++;
while (j < n && nums[j] == nums[j - 1]) {
j++;
}
}
i++;
while (i < n && nums[i] == nums[i - 1]) {
i++;
}
}
return ret;
}
}时间复杂度O(N^3+N * log N),空间复杂度:O(1)