求一个整数x的平方根到指定精度[C++][Python]

这是一道经典的leetcode题目和面试题目，题目如下:

一. 题目描述

LCR 072. x 的平方根

给定一个非负整数 x，计算并返回 x 的平方根，即实现 int sqrt(int x) 函数。

正数的平方根有两个，只输出其中的正数平方根。

如果平方根不是整数，输出只保留整数的部分，小数部分将被舍去。（后面我会补充一下使用牛顿法求到指定精度的例子）

下面的内容有很多参考自Leetcode对这个问题的官方题解

一. 求整形解

解法1: 袖珍计算器法(可以是高精度的)

利用如下的公式进行求解:

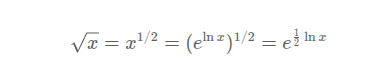
cpp 复制代码

class Solution {
public:
  // 袖珍计算器法
  int mySqrt(int x) {
    // sqrt(x) = exp(0.5*ln(x))
    if (0 == x) {
      return 0;
    }
    int res = exp(0.5 * log(x));
    if (pow(res + 1, 2) <= x) {
      return res + 1;
    }
    return res;
  }
};

python 复制代码

class Solution:
    # 袖珍计算器法
    def mySqrt(self, x: int) -> int:
        if 0 == x:
            return 0
        res:int = int(math.exp(0.5*math.log(x)))
        if pow(res+1, 2)<=x:
            return res+1
        return res

解法2: 二分查找法(只能取整)

cpp 复制代码

class Solution {
public:
  // 二分查找法
  int mySqrt(int x) {
    int l = 0, r = x, mid = -1, ans = -1;
    while (l <= r) {
      mid = l + (r - l) / 2;
      if (x < (long)mid * mid) {
        r = mid - 1;
      } else if (x == (long)mid * mid) {
        return mid;
      } else {
        l = mid + 1;
        ans = mid;
      }
    }
    return ans;
  }
};

python 复制代码

class Solution:
    def mySqrt(self, x: int) -> int:
        l:int = 0
        r:int = x
        ans:int = -1
        while l <= r:
            mid:int = l + (r-l)//2
            if x < mid*mid:
                r = mid-1
            elif x == mid*mid:
                return mid
            else:
                l = mid+1
                ans = mid
        return ans

解法3: 牛顿法(可以高精度)

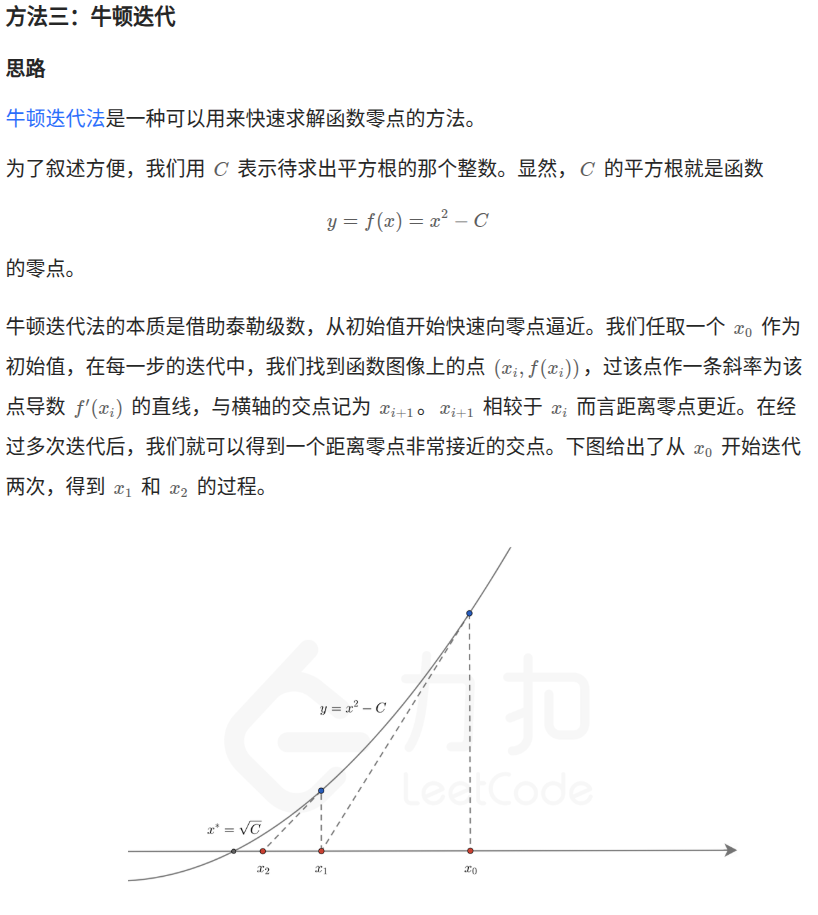
cpp 复制代码

class Solution {
public:
  // 牛顿迭代法
  int mySqrt(int x) {
    if(0 == x){
      return 0;
    }
    int C = x;
    double x0 = x, xi;
    while(true){
      xi = 0.5 * (x0 + C/x0);
      if(fabs(xi-x0)<1e-7){
        break;
      }else{
        x0 = xi;
      }
    }
    return int(xi);
  }
};

python 复制代码

class Solution:
    def mySqrt(self, x: int) -> int:
        if 0 == x:
            return 0
        C:int = x
        x0:float = x
        xi:float
        while True:
            xi = 0.5 * (x0 + C/x0)
            if math.fabs(xi-x0)<1e-7:
                break
            else:
                x0 = xi
        return int(xi)

二. 求指定精度解

上面的这些输出的都是向下取整之后的整数根，如果想要输出指定精度位数的小数的话，需要对代码进行适当的一些修改。

解法1: 袖珍计算器法(可以是高精度的)

利用如下的公式进行求解:

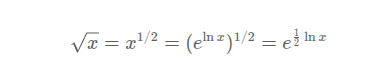
cpp 复制代码

class Solution {
public:
  // 袖珍计算器法
  double mySqrt(int x, int n) {
    // sqrt(x) = exp(0.5*ln(x))
    if (0 == x) {
      return 0;
    }
    double res = exp(0.5 * log(x));
    if (pow(res + 1, 2) <= x) {
      return res + 1;
    }
    //不是四舍五入，是直接舍弃掉后面的
    res = (int)(res * pow(10, n)) / pow(10, n);
    return res;
  }
};