我们在数字信号处理课程当中学习了如何利用Z变换分析信号和系统的频率响应,在此希望对这部分知识进行实践,所以可以想到对常用的滤波器进行设计。

目录
[2.简单一阶滤波器的设计(1st-order System)](#2.简单一阶滤波器的设计(1st-order System))
[4.数字陷波器的设计(Trap filter)](#4.数字陷波器的设计(Trap filter))
[5.全通滤波器的设计(All-Pass filter)](#5.全通滤波器的设计(All-Pass filter))
[6.最小相位滤波器的设计(Minimum-Phase filter)](#6.最小相位滤波器的设计(Minimum-Phase filter))
1.设计数字滤波器的一般原则
(1)若使设计的滤波器拒绝某个频率 (不让该频率信号通过),应在单位圆上相应频率处设置一个零点
(2)若使设计的滤波器突出某个频率 (使该频率信号尽量无衰减的通过),应在单位圆内相应的频率处设置一个极点,极点越接近单位圆,在该频率处的幅频响应幅值越大。
2.简单一阶滤波器的设计(1st-order System)
仅由一个零点或者极点调节系统滤波特性;
我们知道在单位圆上:
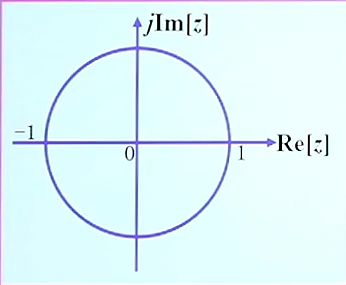
系统的幅频特性为:
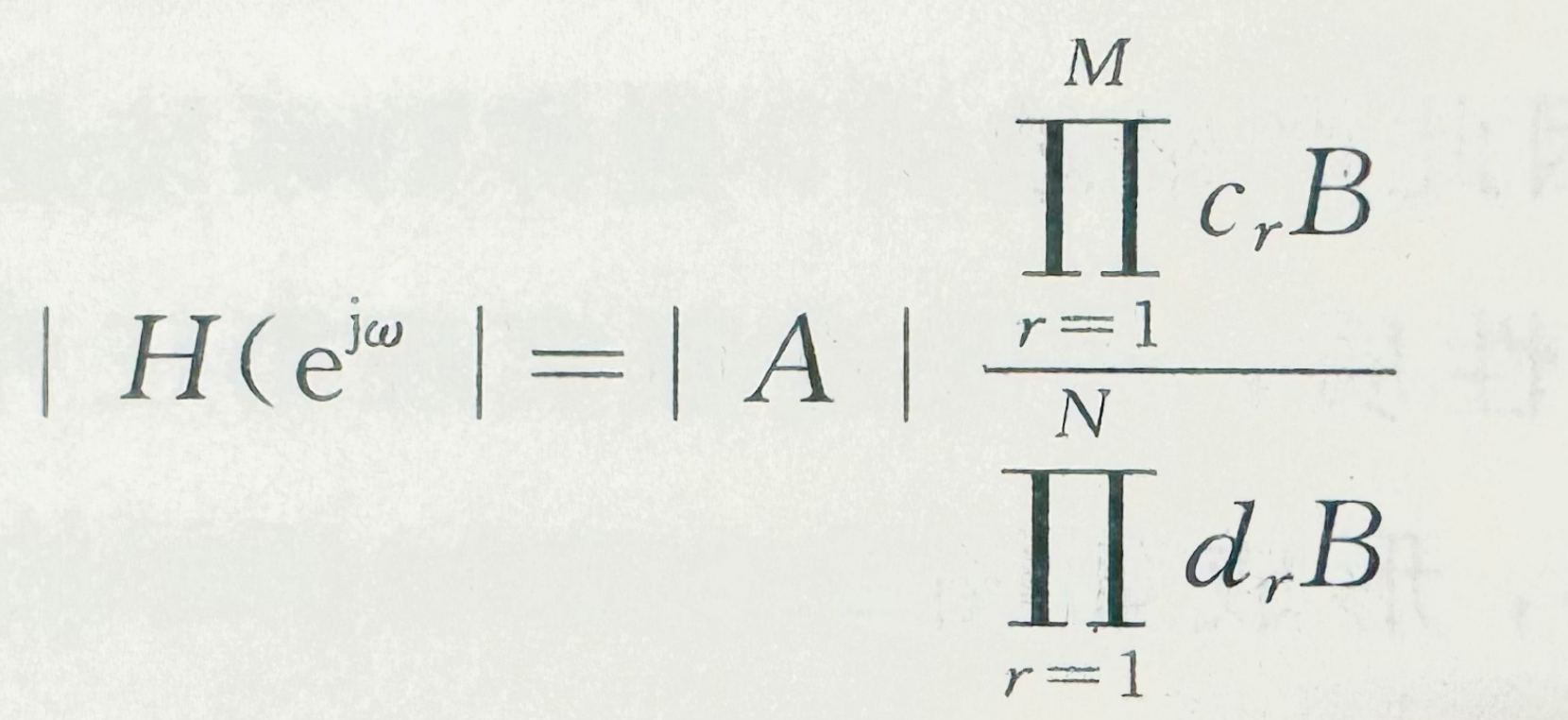 ---式1
---式1
(1)由一个零点调节的低通滤波器
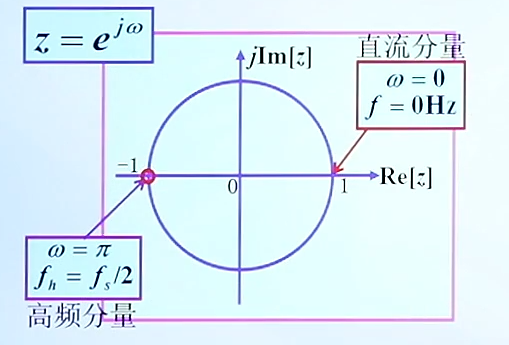
其中fs/2是折叠频率,系统能够通过的最高频率成分,所以在该位置放置一个零点;可以得到,当频率B点在ω=0处,式1的分子最大,可以通过;当B点在ω=pi处时,分子为0,从而不同;且这种状态是随着ω从0到pi,越到高频越不畅通;从而达到一个低通滤波的效果。
我们写出我们的系统函数:

但是我们发现系统是非因果的,所以对其补一个极点,做一个一阶延迟:
注:圆心处的零极点,不会影响系统的幅频响应
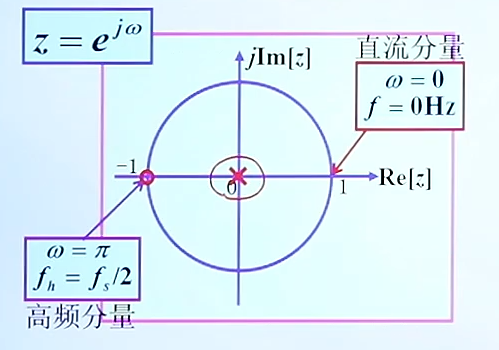
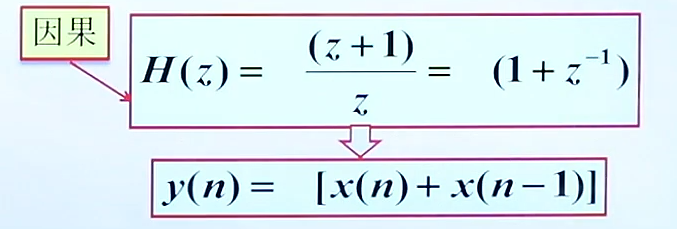
我们希望最大幅度的地方归一化为1,而位置就在ω=0的地方,且最大幅度为2,所以补上一个1/2。
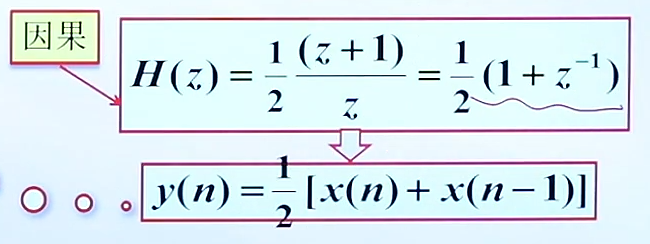
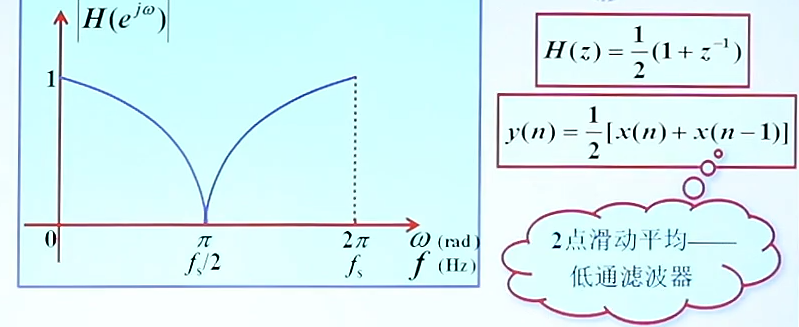
最后不难看出,这个就是我们的2点滑动平均滤波器 ,这就解答了有些时候我们会产生疑惑,均值滤波,按理说滤除的是高幅度的值,为什么也可以滤除我们的高频噪声,和频率有关了?这里我们的推导可以看到,它可以滤去高频(即高频量的幅值衰减到0),也是一个低通滤波器。
那我们同理可以得出一个简单的高通滤波器:(差分系统可以提取出我们的高频成分)
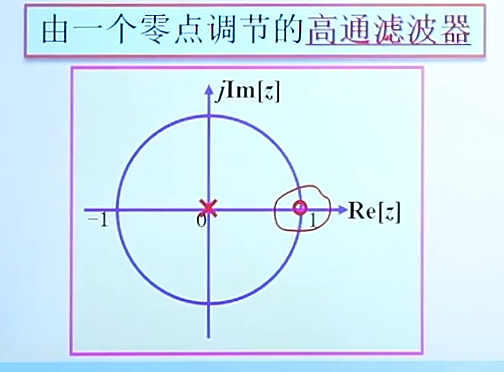
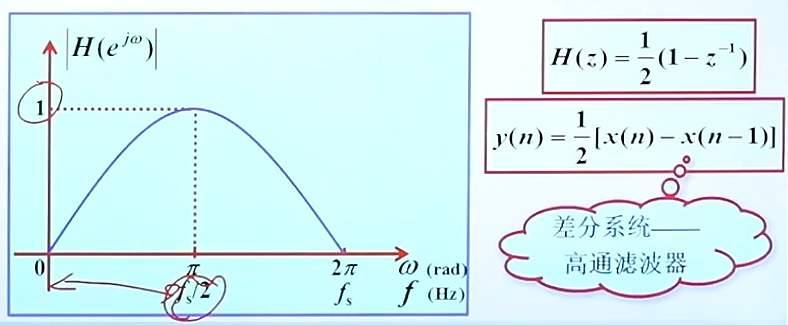
(2)由一个极点调节的低通滤波器
如果,用一个极点来设计一个低通滤波器,我们应该要把极点放在ω=0,并且靠近单位圆的位置,从而当频率即B点靠近低频时,式1的分母很小,靠近高频时,分母很大;
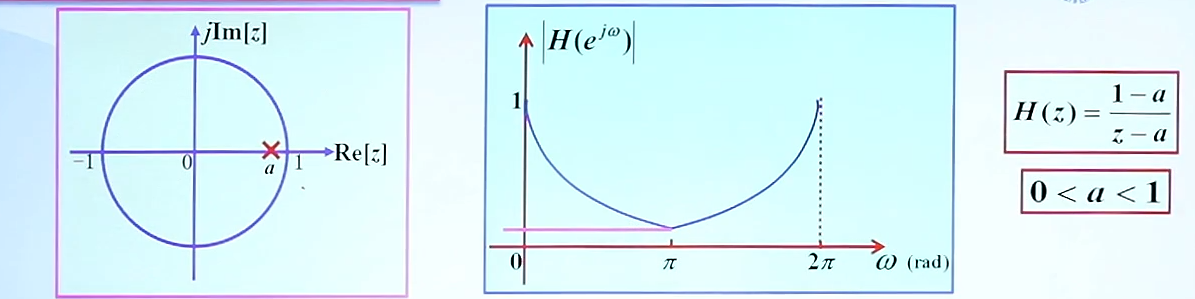
当我们需要在pi的位置,幅度为0,那我们就需要补一个零点在ω=pi的位置上:
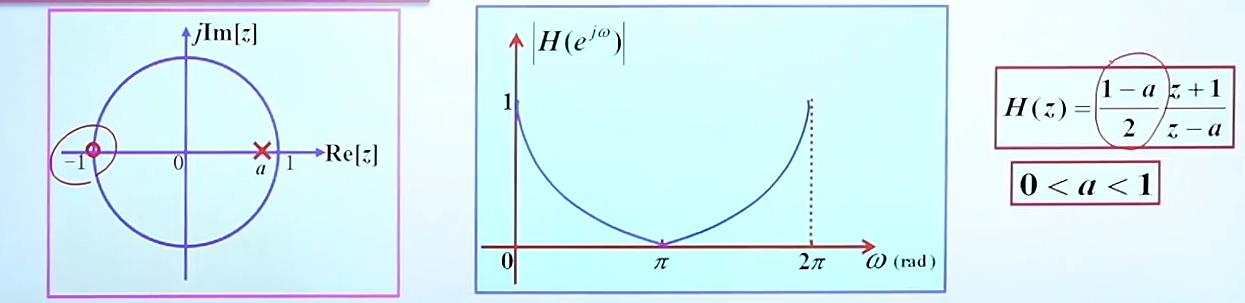
(3)一阶低通滤波器的截至频率设计中关于带宽的考虑
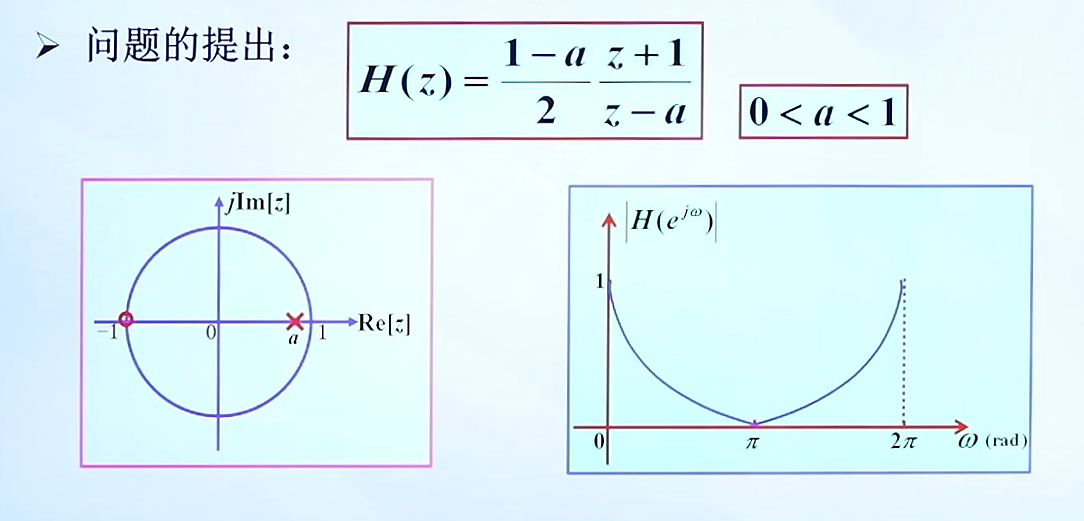
这个时候,我们设计滤波器,希望有一些频段的值通过,有一些不通过,我们就要设计我们的带宽,也就涉及到了我们a的值如何选取的问题。
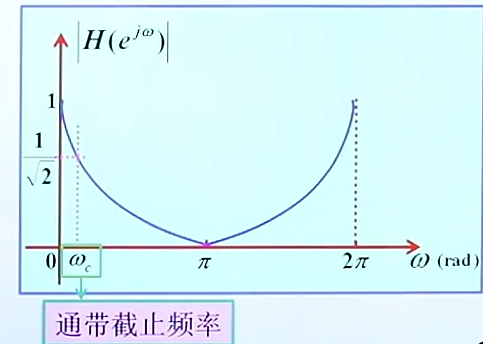
我们最大频率降为1/√2也就是0.707这个位置时,对应的ω就是我们的通带截止频率;也就是信号衰减不能够超过3dB;
通带截止频率与极点位置(a)的关系:
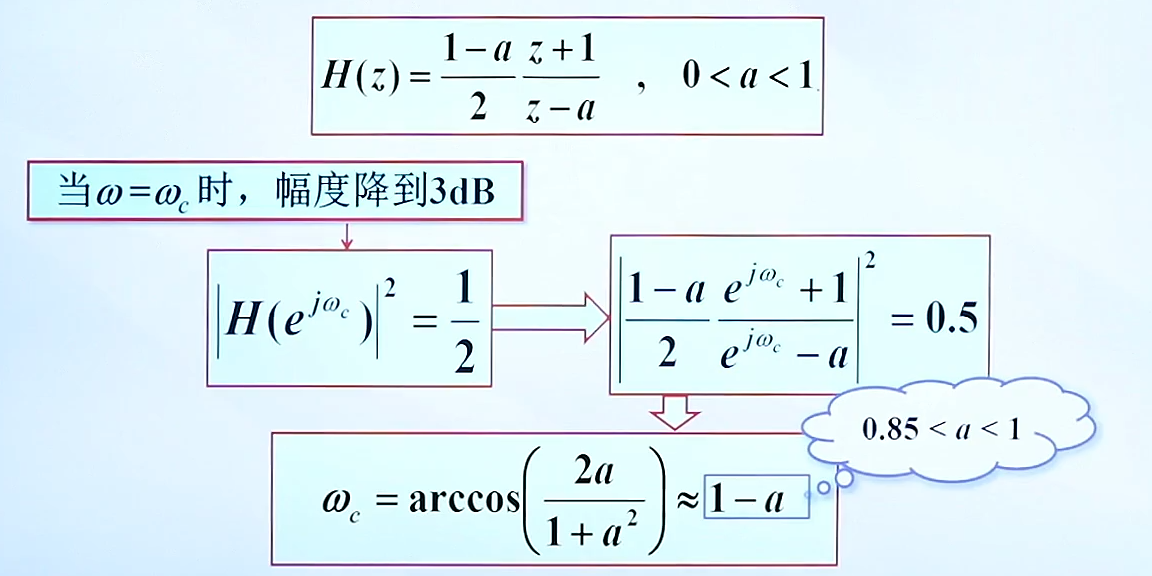
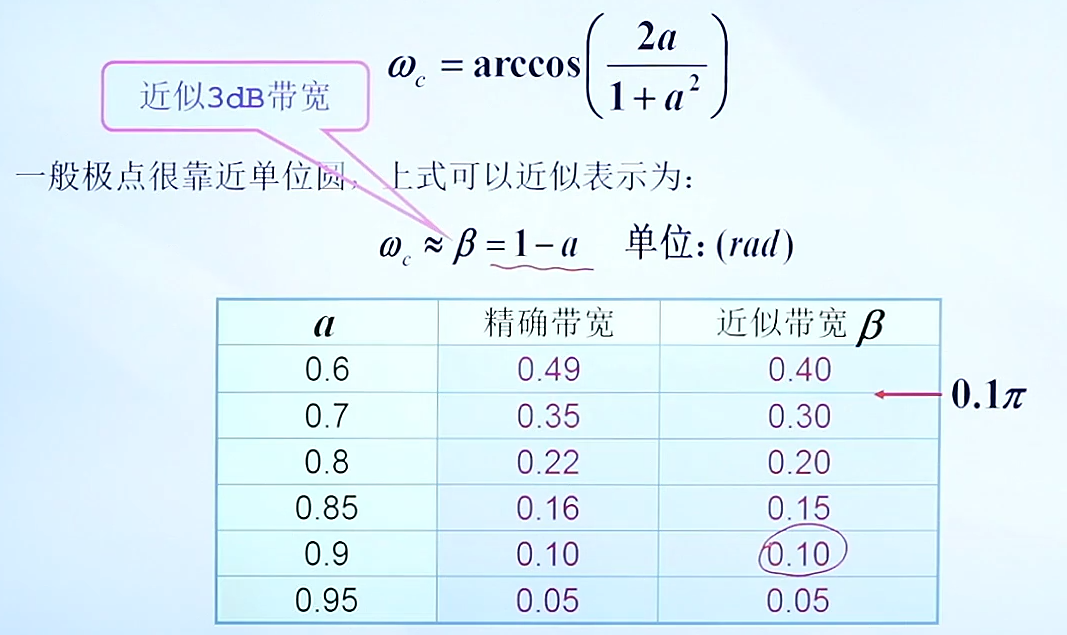
3.数字谐振器的设计(Resonator)
电路里的谐振:当电路中激励的频率等于电路的固有频率时,电路电磁振荡的振幅也将达到峰值。
而我们的数字谐振器就是由输入,得到的输出只凸显我们谐振的那个频率也就是我们想要的那个频率;
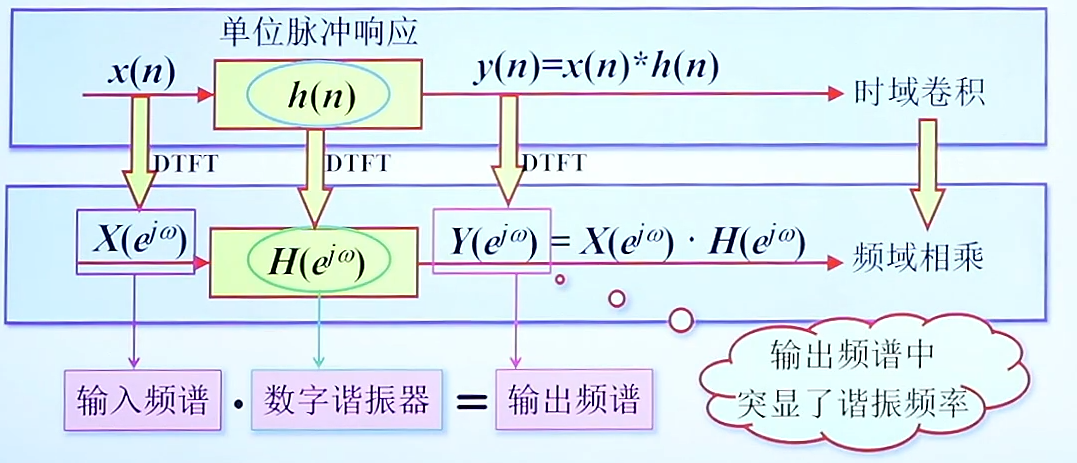
(1)常见的二阶数字谐振器
第一种形式:
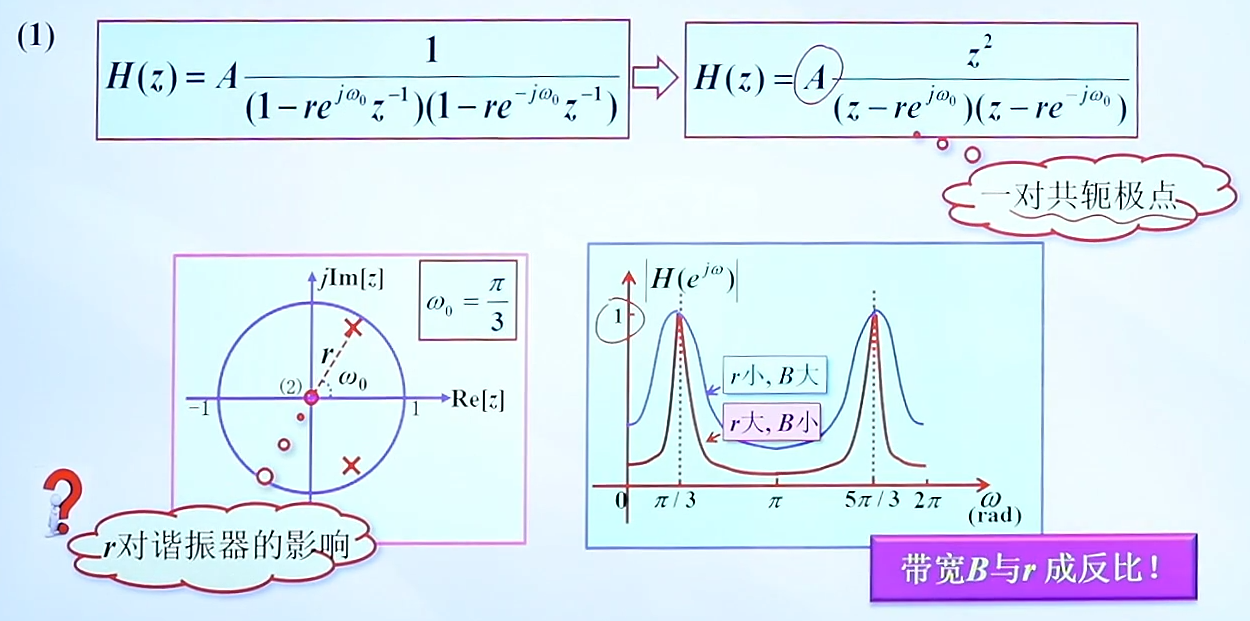
第二种形式:
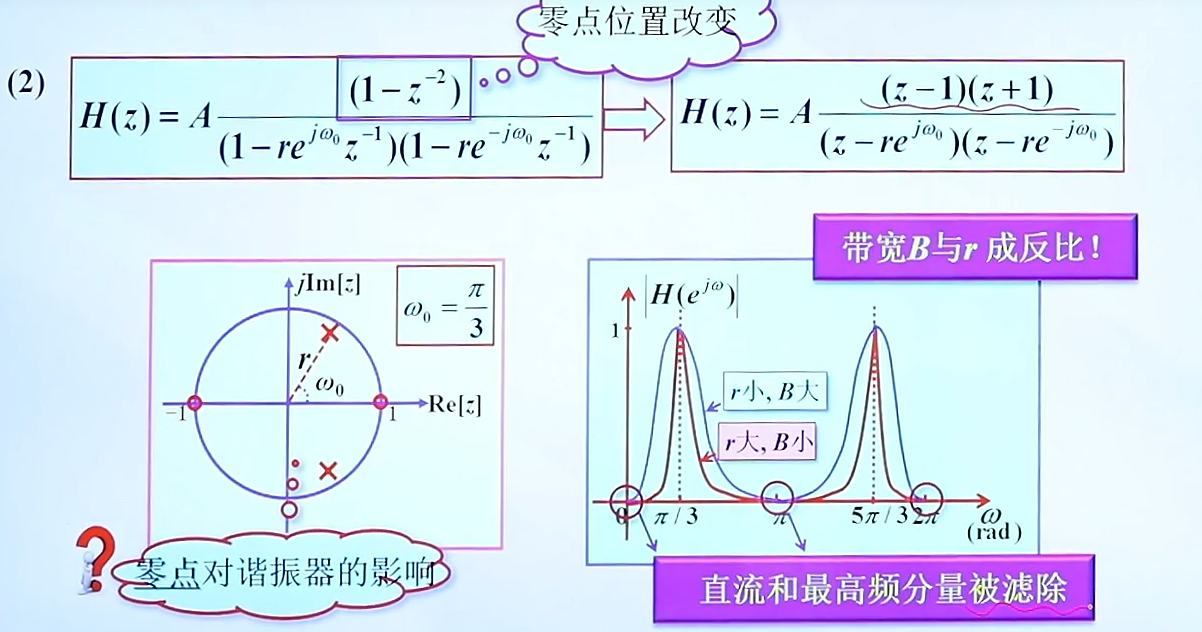
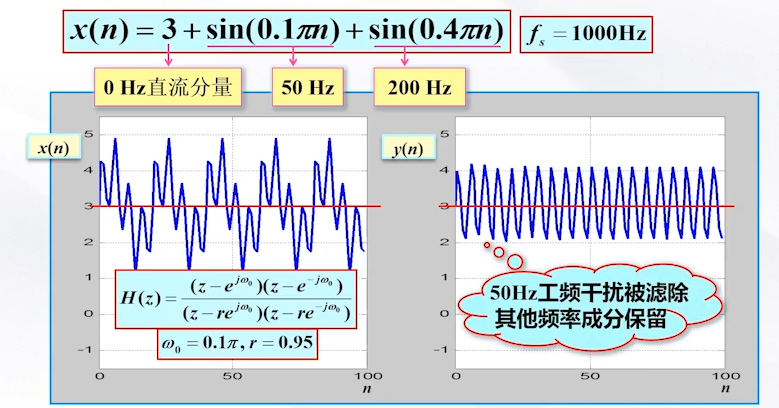
4.数字陷波器的设计(Trap filter)
陷波器 :一种特殊的带阻滤波器,其阻带在理想情况下只有一个频率点,主要用于消除某个特定频率的于扰。
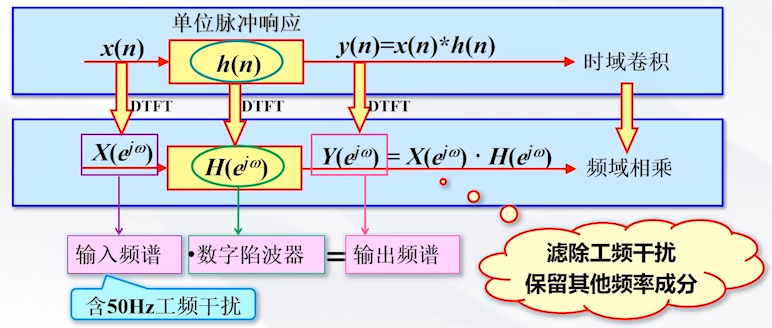
我们先按照正常想法,设计零点消除干扰:
其中,假设我们想滤除一个特定频率 ω0。根据数字信号处理理论,一个在单位圆上、设置角度为 ω0 的零点可以完美滤除这个频率分量。这个零点的位置是:z1=e^{jω0},这是一个复数 。如果我们只放置这这一个复数零点, 系统函数 H(z) 的一部分就是 (1 - e^{jω0} z^{-1})。将其乘开,得到的系数 h[n]会包含e^{jω0},这显然是一个复数(同时包含实部和虚部)
这意味着,要实现这个滤波器,你需要进行复数运算,处理复数的输入和输出。
而这个问题由数学工具可以解决:一个实系数多项式的复根(零点)必须成共轭对出现。也就是说如果 z1 是一个复零点,那么它的共轭 z1* 也必须是这个系统的零点,只有这样,多项式展开后的系数才会全是实数。(因为系数是实数,这个滤波器可以用真实的硬件(如数字信号处理器DSP)或软件程序来实现,处理我们现实中遇到的实信号。)
如下设计:
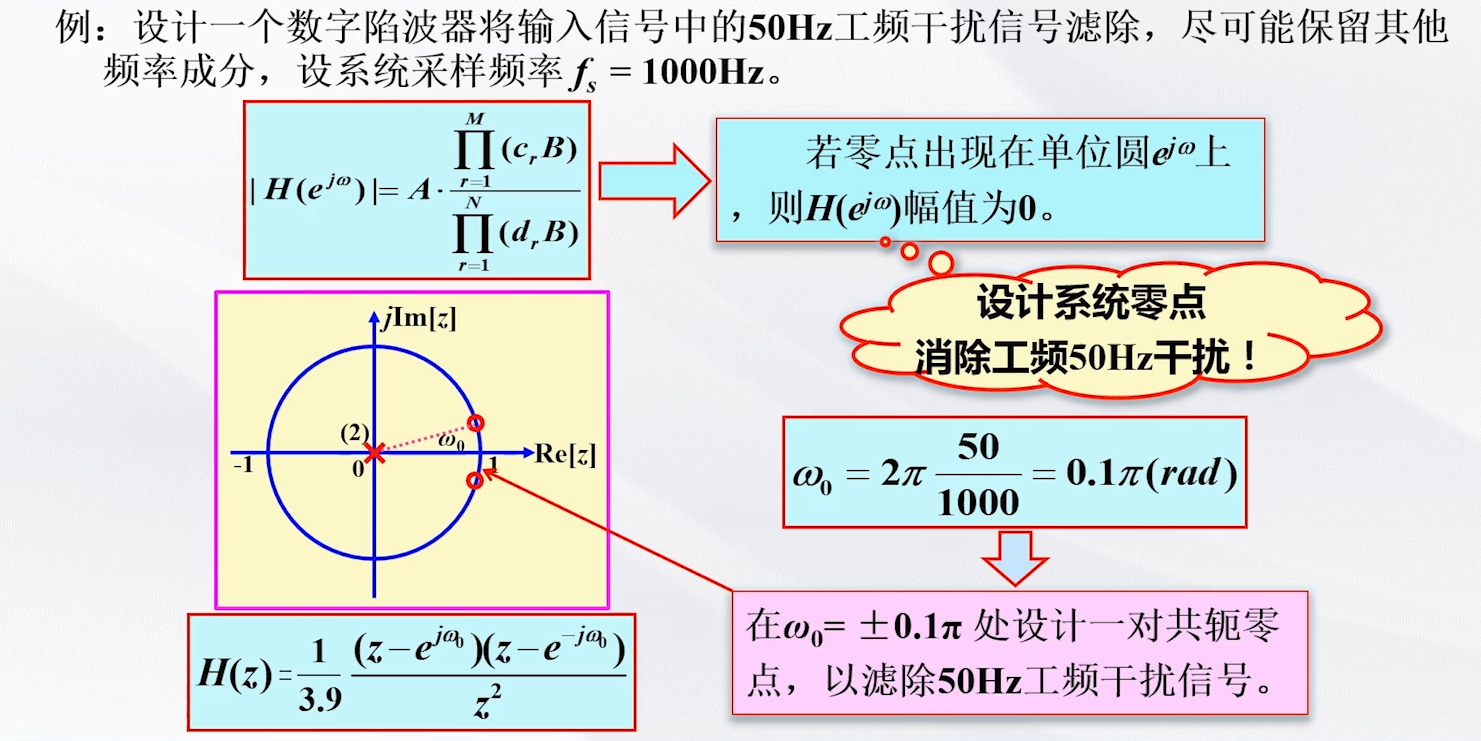
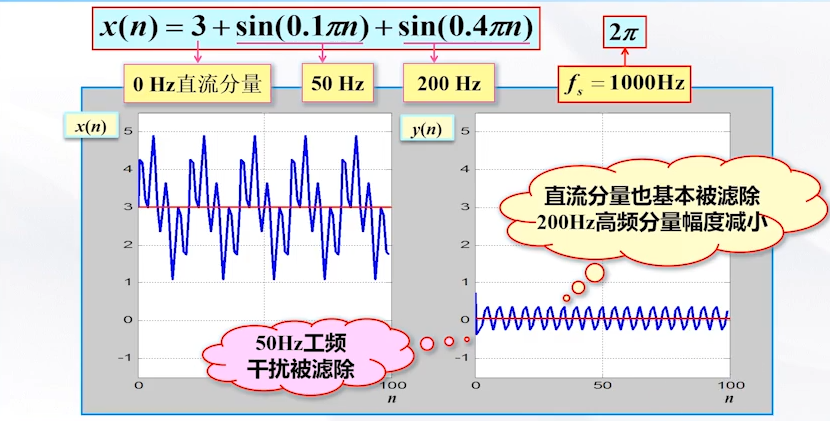
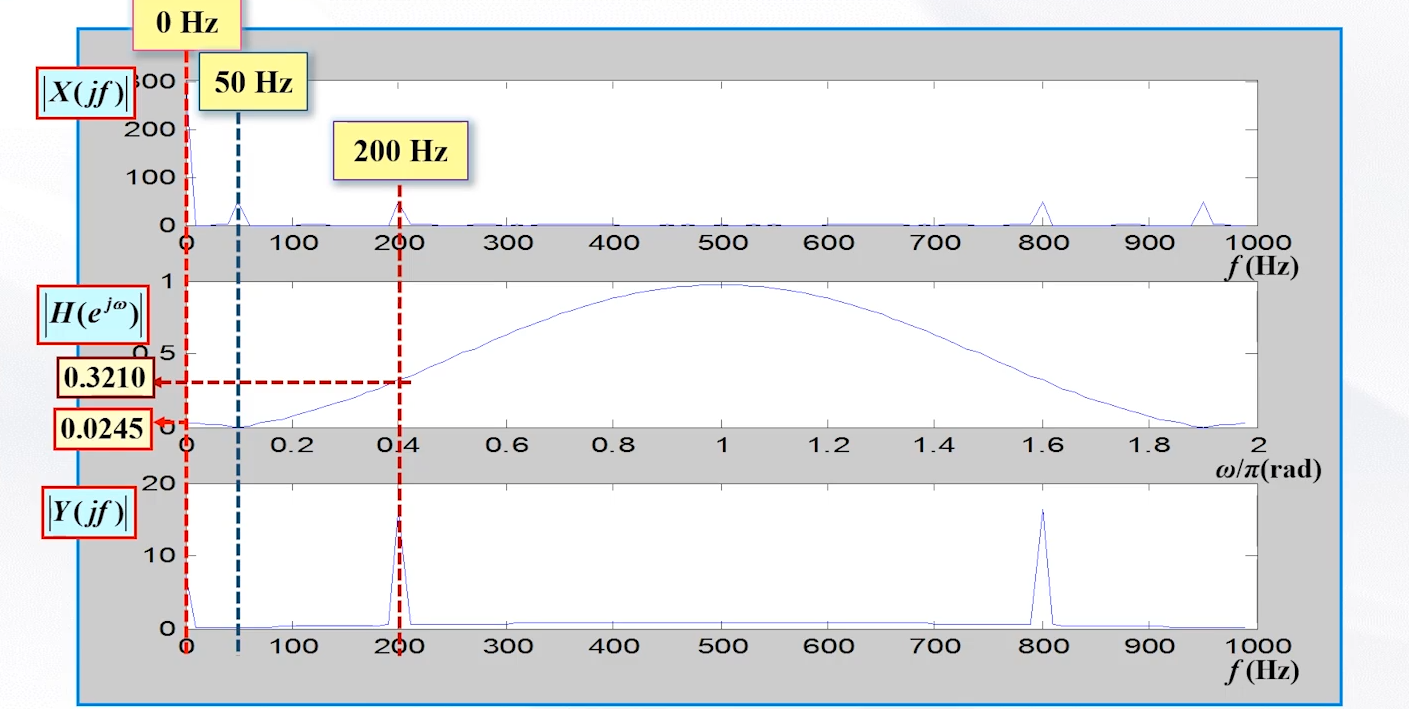
此时我们发现,设计有问题,50Hz确实被滤除了,但0Hz和200Hz我们需要的成分也有一定的滤波效果,这是我们不想要的
此时我们重新考虑来思考这个问题:
我们希望整个系统到了需要滤除的频率跟前要滤下去,不过之后要马上跟上来,不能影响到我们其他频率,使其他频率都约等于1;
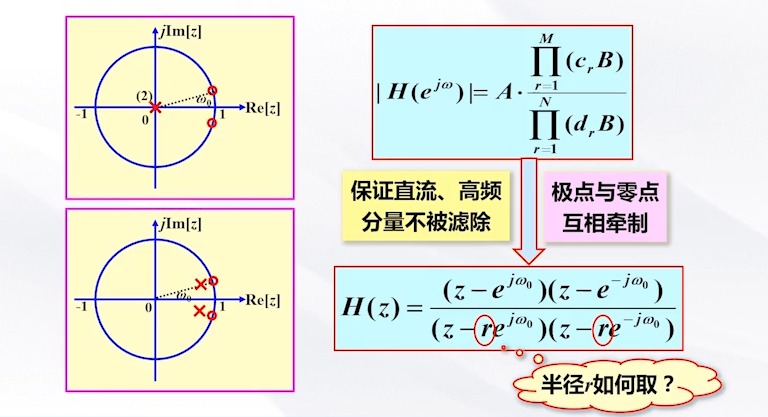
只有cr和dr尽力靠近时,频率的幅频响应约等于1;这里我们就要考虑到r的取值,也就是极点的位置的问题了;
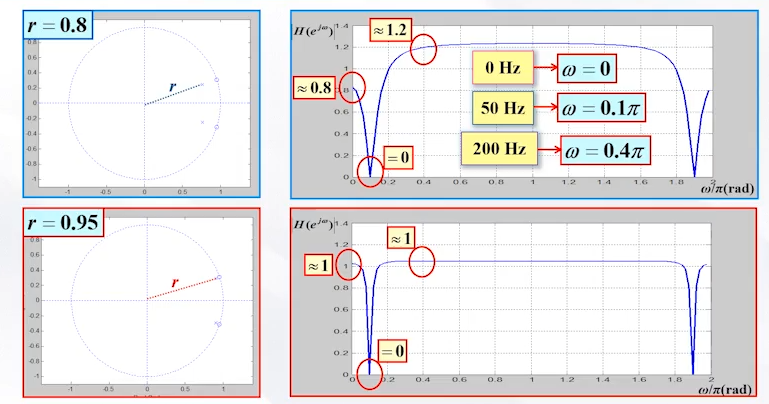
当选取r= 0.95时,效果如下图:从而我们的陷波器就设计好了
5.全通滤波器的设计(All-Pass filter)

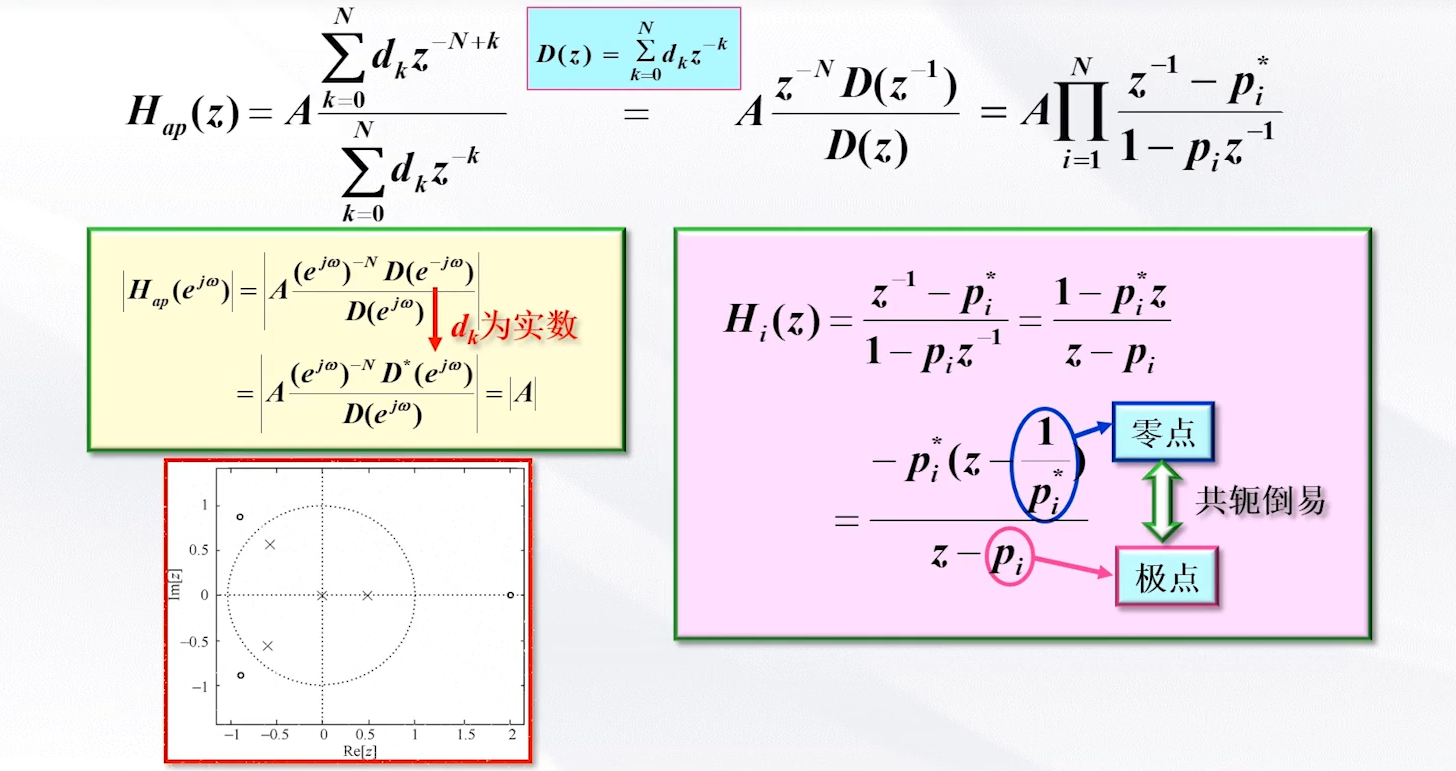
知识点1:全通滤波器的零极点是共轭倒易的关系


我们继续分析其相位响应:

群延迟 是相位响应曲线在某频率点上的斜率 的负值 (τ_g) = - (dφ / dω)
知识点2:实系数因果稳定的全通滤波器的重要特性是,相位在【0,pi】内单调减少;群延迟为正
6.最小相位滤波器的设计(Minimum-Phase filter)
在具有相同幅频响应(即 |H(e^{jω})| 相同)的所有因果稳定滤波器中,最小相位滤波器具有最小的相位延迟(Phase Delay)和最小的群延迟(Group Delay) 。也就是说,它在所有频率上引入的相位滞后是最小的。


因为Hi(z)为1/H(z),其零点变为了逆系统的极点,所以需要零极点都在单位圆内;
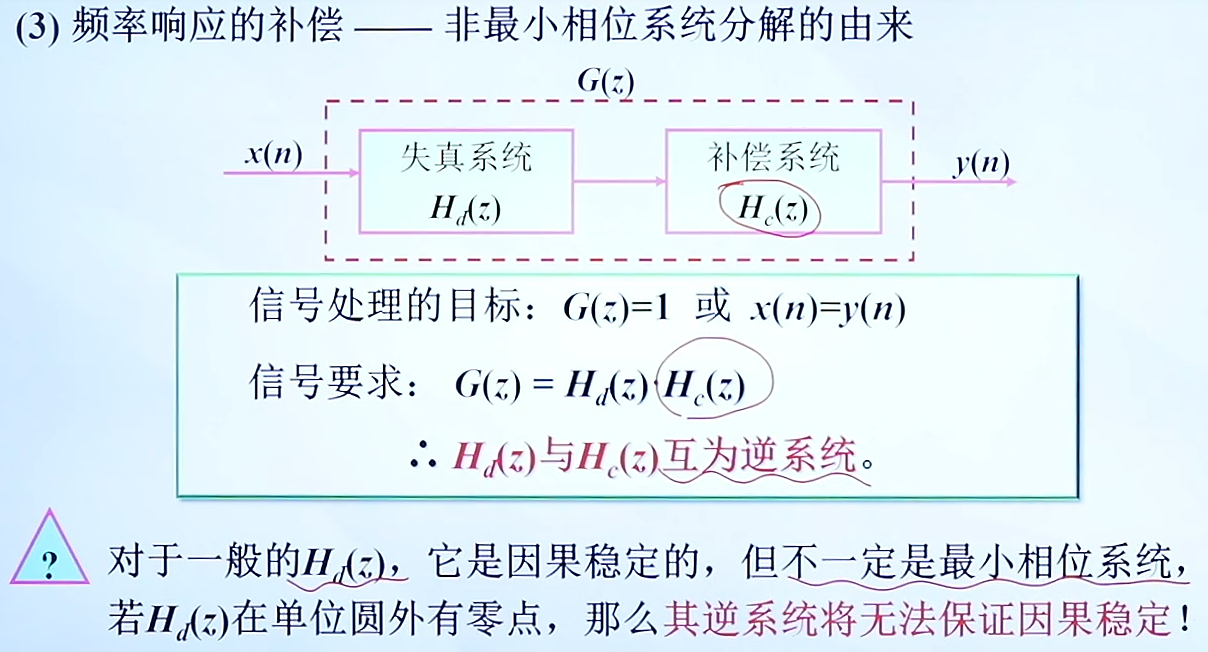
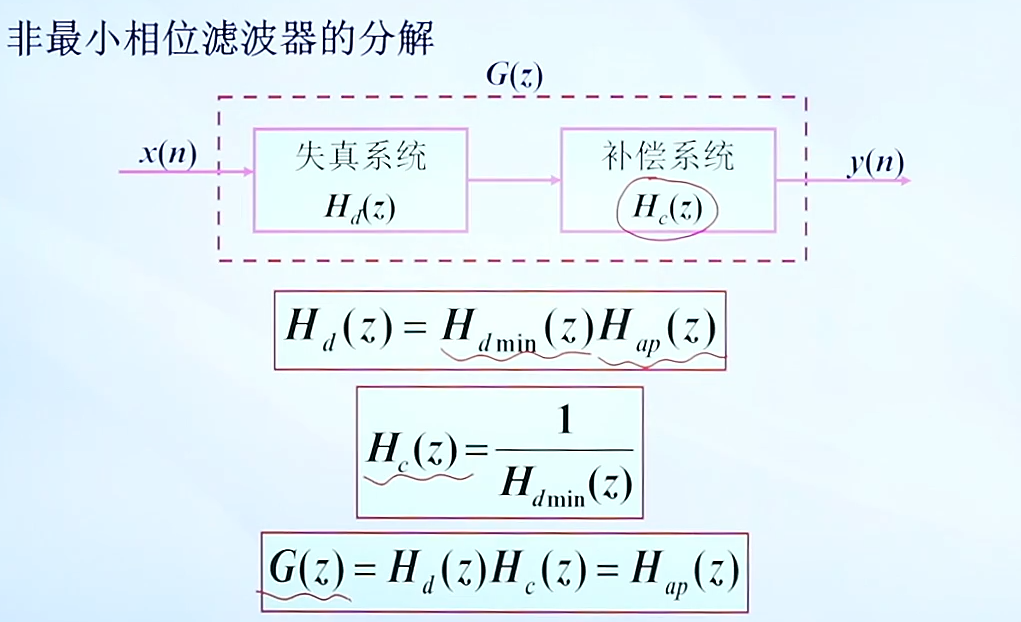
Hdmin(z)是指最小相位 Hap(z)是指全通


7.工程中常用滤波
(1)限幅滤波法
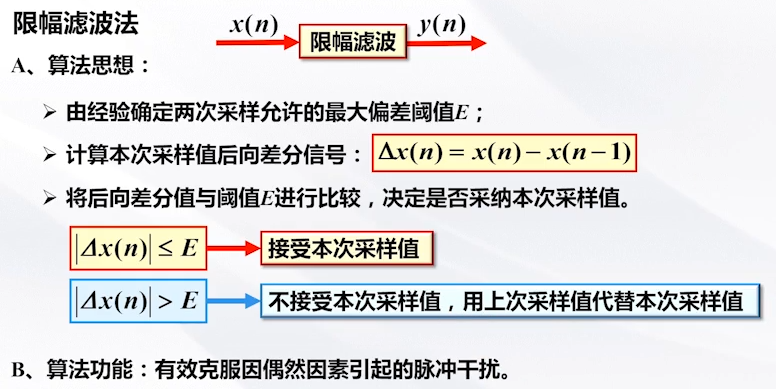
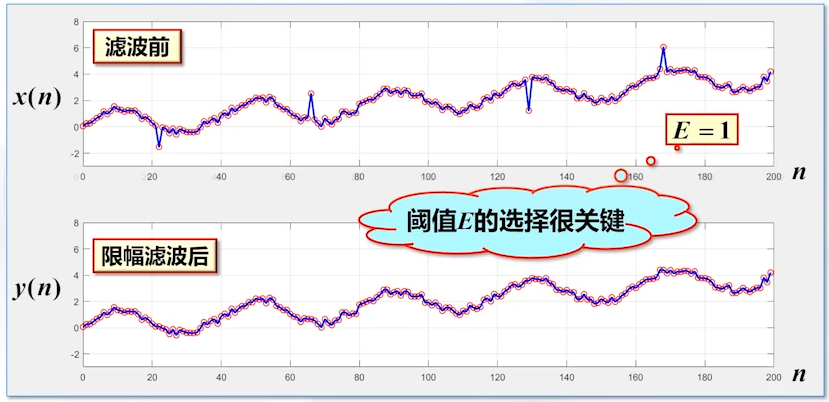
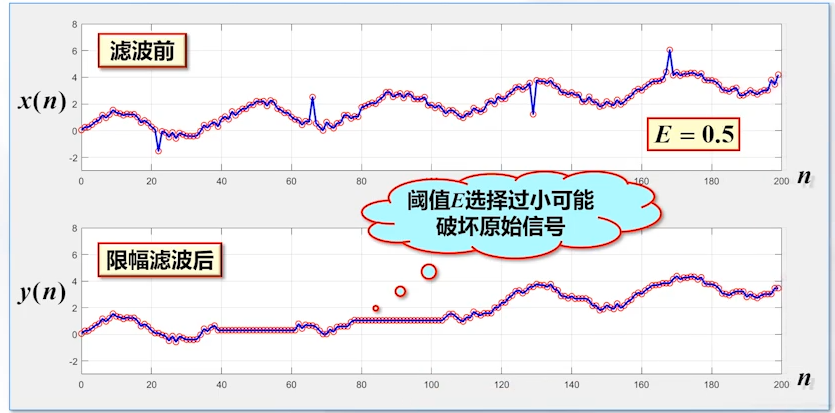
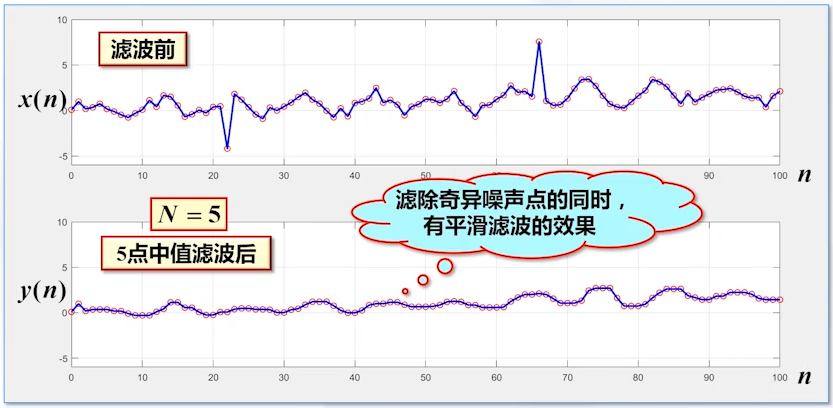
(2)中值滤波法
中值滤波不是一个LSI系统,但是在工程中利用较为广泛

窗口值合适时,我们的噪声被滤除,并且波形在更加平滑
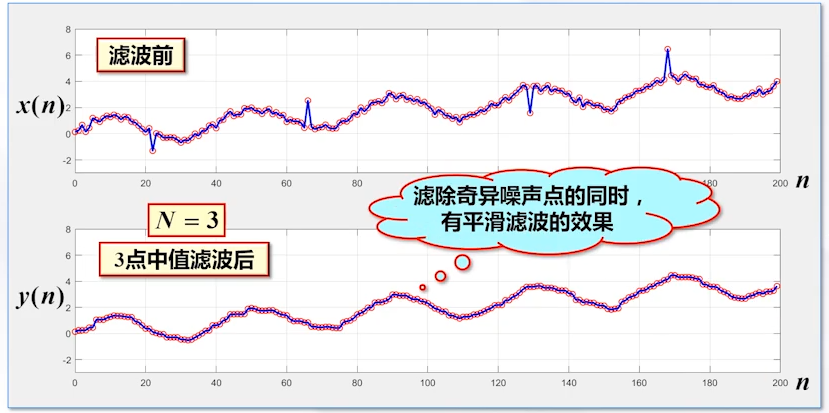
但是窗口值过大,我们的波形过于平滑,从而失真
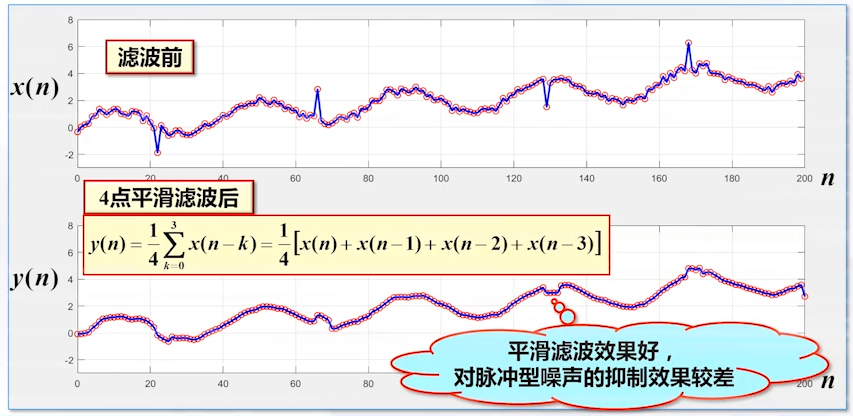
(3)滑动平均滤波法

(4)融合型的滤波法

8.信号中趋势项的去除
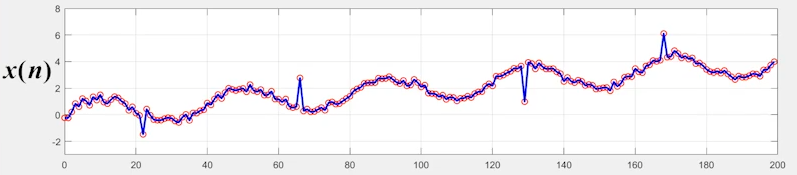
我们看到,这里的信号X(n)有一个向上整体偏移的趋势,因为信号中有零漂的现象,若这并不是我们想要的;我们则需要将其去除。
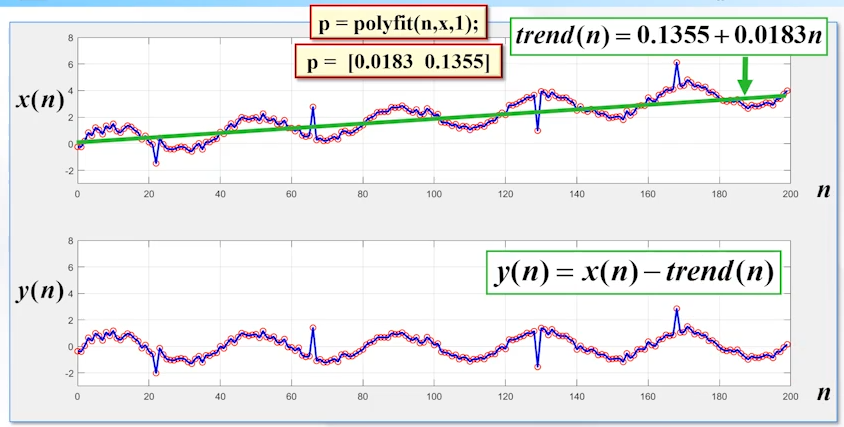
这里我们用到了matlab中的polyfit函数,用于多项式曲线拟合
这里我们选择用一阶曲线拟合,近似得到我们的趋势项,最后输出就是我们输入减去趋势项;从而得到一个比较好的效果。
内容学习自万永菁老师的数字信号处理: