目录
(6)在末尾添加元素在末尾添加元素)
一.线性表
1.定义:
线性表是最基本、最简单、也是最常用的一种数据结构。一个线性表是n个具有相同特性的数据元素的有限序列。
•前驱元素:
若A元素在B元素的前面,则称A为B的前驱元素
•后继元素:
若B元素在A元素的后面,则称B为A的后继元素
2.特征:
-
第一个数据元素没有前驱,这个数据元素被称为头结点;
-
最后一个数据元素没有后继,这个数据元素被称为尾结点;
-
除了第一个和最后一个数据元素外,其他数据元素有且仅有一个前驱和一个后继。
分类:
线性表中数据存储的方式可以是顺序存储,也可以是链式存储,按照数据的存储方式不同,可以把线性表分为顺序表和链表。
二.顺序表
根据前面关于线性表的分类可知,顺序表就是用数组实现对数据的增,删,查,改
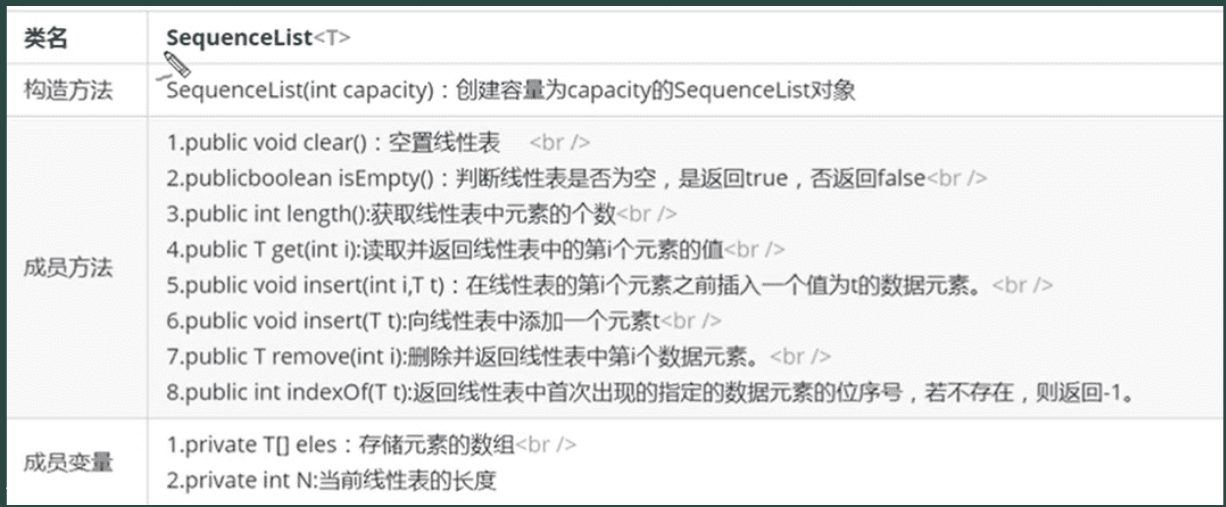
关于顺序表的API设计:
我们现在一一实现这些方法:
代码实现:
(1)首先对顺序表的初始化创建
class SequenceList<T>
{
//用于存储元素的数组
private T[] elem;
//顺序表中的元素个数
private int usedSize;
//-----构造顺序表中的初始容量
public SequenceList(int capacity)
{
elem = (T[]) new Object[capacity];
this.usedSize = 0;
}
}(2)清空顺序表
思路分析:顺序表由数组实现,当我们想要清空顺序表时,只需要将数组的长度重新设置为0即可
//----清空顺序列表
public void clear()
{
this.usedSize = 0;
}(3)判断顺序表是否为空
思路分析:用数组fasle与0比较,等于0则返回true,不等于0则返回false
//------判断列表是否为空
public boolean isEmpty()
{
return usedSize == 0;
}(4)获取元素个数
思路分析:我们设置的usedSize是从0开始的因此直接返回就行
public int length()
{
return usedSize;
}(5)获取对应索引的元素
思路分析:1.先考虑所给索引是否在数组中存在对应的数据,如果给的索引位置不对,则抛出一个异常,停止运行
2.索引位置正确,直接返回
//----获取对应位置的元素
public T get(int i)
{
if(i < 0 || i >= usedSize)
{
throw new RuntimeException("输入位置违规");
}
return elem[i];
}(6)在末尾添加元素
思路分析:1.先判断数组元素是否已满,如果已满的话,我们需要进行扩容
2.数组从索引0开始,只需要把新元素添加到elem[usedSize] 中即可
3.别忘了将数组元素加一
//----如果数组满就对数组进行扩容
public void checkCapacity()
{
if(usedSize == elem.length)
{
T[] newElem = (T[]) new Object[elem.length * 2];
}
}
//----在末尾添加元素
public void add(T data)
{
//先判断数组元素是否已满,已满则进行扩容
checkCapacity();
this.elem[usedSize] = data;
this.usedSize++;
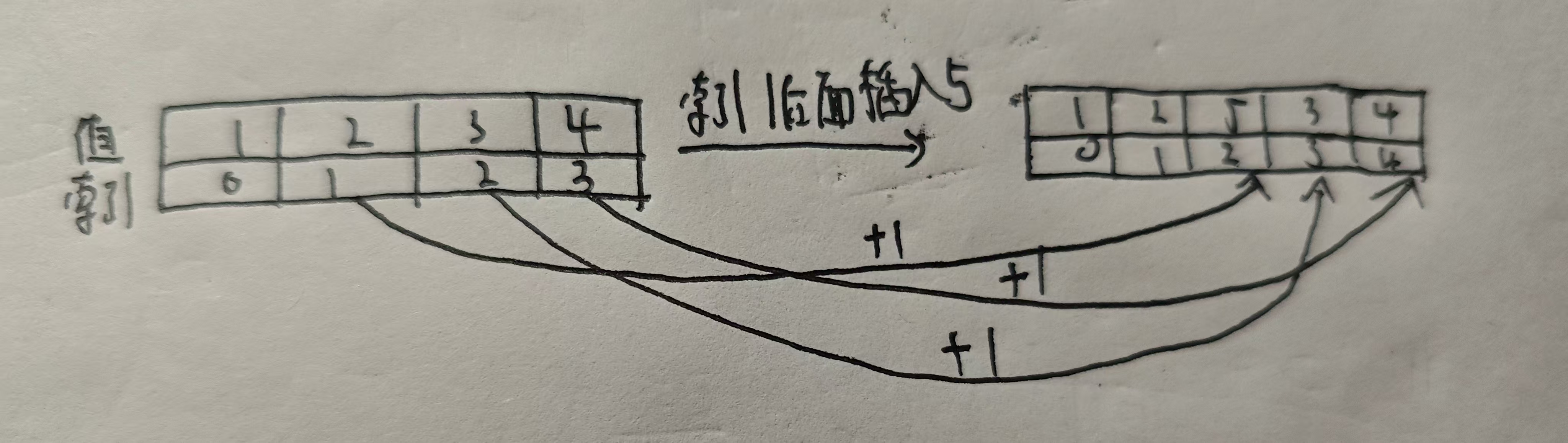
}(7)在指定位置插入元素
思路分析:1.先检查输入的位置是否合规,不合规,则抛出异常,终止运行
2.依然先判断数组元素是否已满
3.插入新元素后,在指定位置后面的元素都要往后退1,我们便从最后一个元素开始挪动,直到挪到了指定位置
//-----在指定位置后面插入元素
public void add(int index, T data)
{
//先检查输入位置是否合法
if(index < 0 || index > usedSize)
{
throw new RuntimeException("输入位置违规");
}
//判断数组是否有剩余空间
checkCapacity();
//开始从最后一个有效元素挪动
for(int i=usedSize-1; i>=index; i--)
{
this.elem[i+1] = elem[i];
}
elem[index] = data;
usedSize++;
}(8)查找某个元素的下标
思路分析:使用循环,遍历数组,用equals函数找到我们想要的元素,这时对应的下标也找到了
//----查找某个元素的下标位置
public int indexOf(T toFund)
{
//从头变例数组,用一个equals函数找到与toFund相等的元素,找不到就返回-1
for(int i=0; i<usedSize; i++)
{
if( elem[i].equals(toFund))
{
return i;
}
}
return -1;
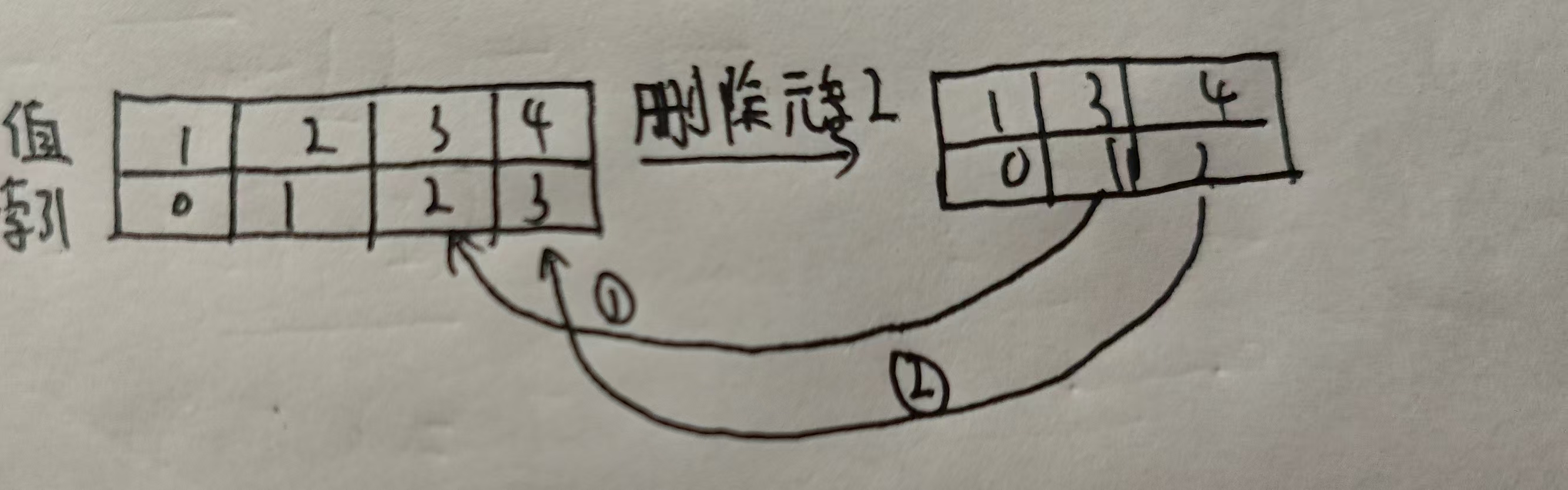
}(9)删除指定元素
思路分析:1.首先需要找到元素所对应的索引,如果没找到就返回
2.类比在指定位置添加元素,我们应该从被删除后的下一个元素开始依次往前挪动1
//-----删除指定元素
public boolean remove(T key)
{
//找到数据对应的索引
int index =indexOf(key);
if(index ==-1)
{
System.out.println("未找到该数据");
return false;
}
//从删除元素的后一位开始挪动
for(int i=index+1; i<=usedSize-1; i++)
{
this.elem[i-1] = elem[i];
}
usedSize--;
return true;
}补充(10)打印顺序表
思路分析:用循环遍历数组即可
//-----打印顺序表中的学生姓名
public void printAll()
{
for (int i=0; i<usedSize; i++)
{
System.out.println(elem[i]);
}
}让我们通过一道练习题,检验这些方法
练习题:
假设你正在开发一个简单的学生管理系统,使用顺序表(SequenceList)来存储学生姓名。请完成以下任务:
1、创建一个可以存储字符串的顺序表,初始容量为10

2、添加以下学生姓名到顺序表中:"张三", "李四", "王五","赵六"。

3、在"李四"后面插入"李四"(注意:需要先找到"李四"的位置)


4、删除"李四"并从顺序表中移除


5、查找"李四"在顺序表中的位置(索引)

6、打印最终顺序表中的所有学生姓名

7、清空顺序表并验证它确实为空