上述内容因为不考虑b的问题,实际上不是完整的线性回归,本章考虑b的因素,实现一个完整的且结构最简单的线性回归问题。
++本章使用数学方法实现的意思是自己通过代码求导数,这个过程只是方便理解,后续会统一使用框架解决,不要过度纠结于计算和画图代码本身。++
1 线性回归
定义:线性回归是一种用于建立自变量与因变量之间关系的统计方法。
它假设因变量(或响应变量)与一个或多个自变量(或预测变量)之间的关系是线性的。
其主要目标是通过拟合一个线性模型来预测因变量的数值。
2 线性回归方程
线性回归模型可以表示为:

**目标:**线性回归的目标是找到最佳的系数来使模型与观察到的数据尽可能拟合。
线性回归的应用
预测:给定自变量的值,预测因变量的值。
回归分析:确定自变量对因变量的影响程度。
总结
线性回归是统计学和机器学习中最简单且最常用的技术之一,它提供了一个基本框架来理解和分析变量之间的的关系,并用于许多实际应用中,如经济学、金融学、医学、社会科学等领域。
3 相关概念
参数:
模型中可调整的变量,它们用来捕捉数据中的模式和特征。这些参数在模型训练过程中被不断调整以最小化损失函数或优化某种目标。例如之前的w和b参数。
权重(Weights):
用来表示不同输入特征与神经元之间的连接强度。
偏置(Biases):
用于调整每个神经元的激活阈值,使模型能够更好地拟合数据。
超参数:
不是通过训练数据学习得到的,而是在训练过程之前需要手动设置的参数 。包括学习率、正则化参数、迭代次数、批量大小、神经网络层数和每层的神经元数量与激活函数等。例如之前的K。
以下概念之前和后续都会学到,灰色参数仅供了解。
学习率(Learning Rate) :用于控制优化算法中每次更新参数时的步长。较小的学习率会导致训练收敛较慢,而较大的学习率可能导致训练不稳定或震荡。
正则化参数(Regularization Parameter) :用于控制正则化的强度,如L1正则化和L2正则化。较大的正则化参数会增强正则化效果,有助于防止*++过拟合++*。
迭代次数(Number of Iterations) :用于控制训练的迭代次数。迭代次数太小可能导致模型未完全学习数据的特征,而迭代次数太大可能导致过拟合。
批量大小( Batch Size**)**:用于控制每次训练时用于更新参数的样本数量。批量大小的选择会影响训练速度和内存消耗。
神经网络层数和每层的神经元数量(Number of Layers and Neurons per Layer):用于定义神经网络的结构。
激活函数(Activation Function):用于控制神经网络每个神经元的输出范围,如Sigmoid、ReLU等。
4 自求导的方法实现线性回归算法
代码运行步骤:
散点输入→参数初始化→损失函数→开始迭代→反向传播→显示频率设置→梯度下降显示
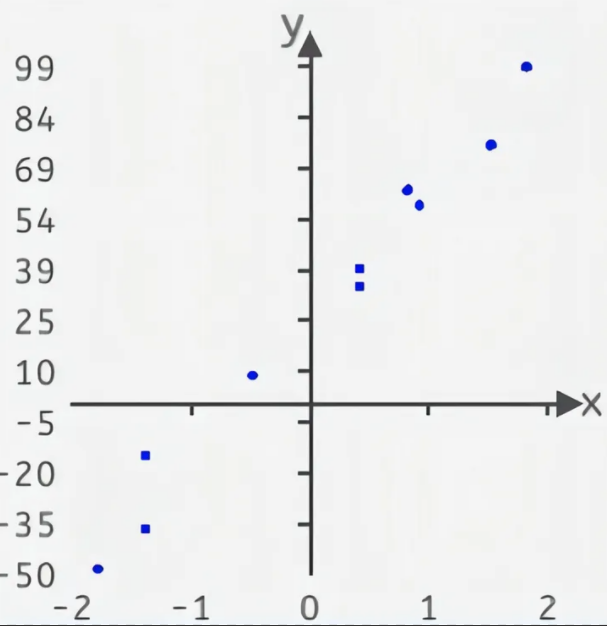
4.1 散点输入
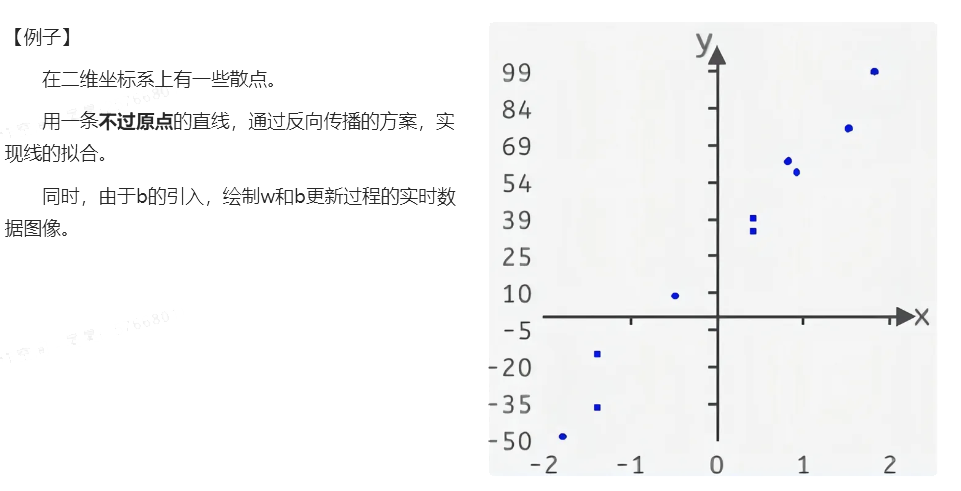
4.2 参数初始化
在前向传播实验中,知道了参数不同时对应的损失函数值也不同,所以需要先初始化一下参数和超参数,进行一次前向传播,得到损失值,这样才能通过反向传播减小损失,使直线的拟合效果更好。这里通过"参数初始化"组件来初始化w和b以及学习率这三个参数/超参数。无论初始化的参数wb是什么,理论上都可以得到理想的结果。
4.3 损失函数
与前向传播实验和反向传播实验不同,此时b的值不再是0,也就意味着损失函数不仅仅受到w的影响,还会受到b的影响,将 y=wx+b 带入损失函数的表达式后,新的损失函数就变成了如下图所示的表达式:

4.4 开始迭代
迭代次数通常指的是反向传播的次数,即通过反向传播来更新模型的参数,直到达到一定的迭代次数或者达到收敛的条件为止。
迭代的次数越多,模型参数就越接近最优解,从而使得损失函数达到最小值,但是可能会造成过拟合(过拟合在之后的实验会讲到)。
一般来说,迭代次数需要根据具体情况来确定,通常需要进行多次迭代来更新模型参数,直到达到收敛的条件为止。
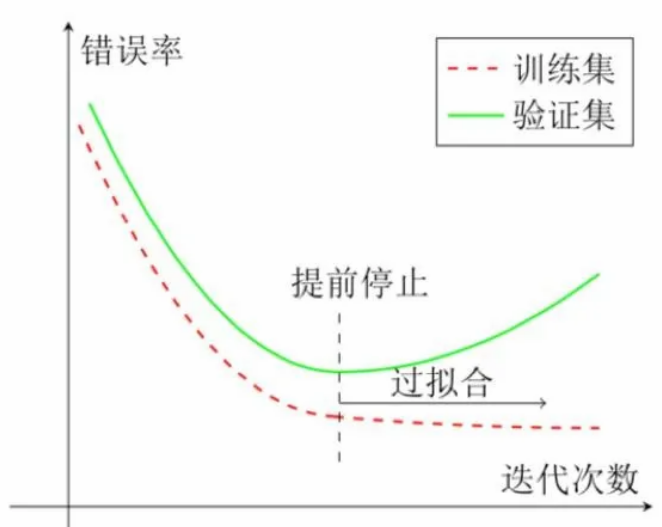
机器学习的准确率满足需求后,继续迭代可能会出现过拟合情况,此时应该使用早停法。
过拟合(Overfitting)是机器学习中一个常见的问题,指的是模型在训练数据上表现得非常好,但是在新的、未见过的数据上表现不佳的现象。换句话说,模型学习到了训练数据中的噪声(没有完美的数据)和细节,而不仅仅是底层的数据分布。
早停法(Early Stopping,即提前停止):在验证集上的性能不再提升时停止训练。属于比较简单粗暴的过拟合解决方法。
4.5 反向传播
反向传播可以自动求导。当参数和损失函数都设置好之后,就开始反向传播了,也就是损失函数对w和b进行求导并且不断更新w和b的过程,是一个复合函数求导的过程。损失函数对w和b的求导过程如下:

需注意,左图中的最终结果单点误差(损失函数),实际计算要考虑到所有的店的均方误差:
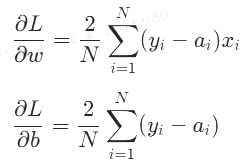
4.6 显示频率设置
求导完成之后,使用梯度下降的方法来更新w和b的值。为了更好的在实验中看现象,这里有一个"显示频率设置"组件,就是每经过多少次迭代,绘制一次当前参数的拟合线及损失函数的大小。
4.7 梯度下降显示
迭代的结果通过"梯度下降显示"进行查看。
代码运行,使用JupyterLab写代码
