本篇文章主要是记录在学习tensorflow框架过程中的核心知识点、踩过的坑、以及一些实战代码。 配置环境
操作系统:MacBook Pro,2.6 GHz 六核Intel Core i7。 python version:3.7 tensorflow version:1.15
TensorFlow基础概念
模块与API
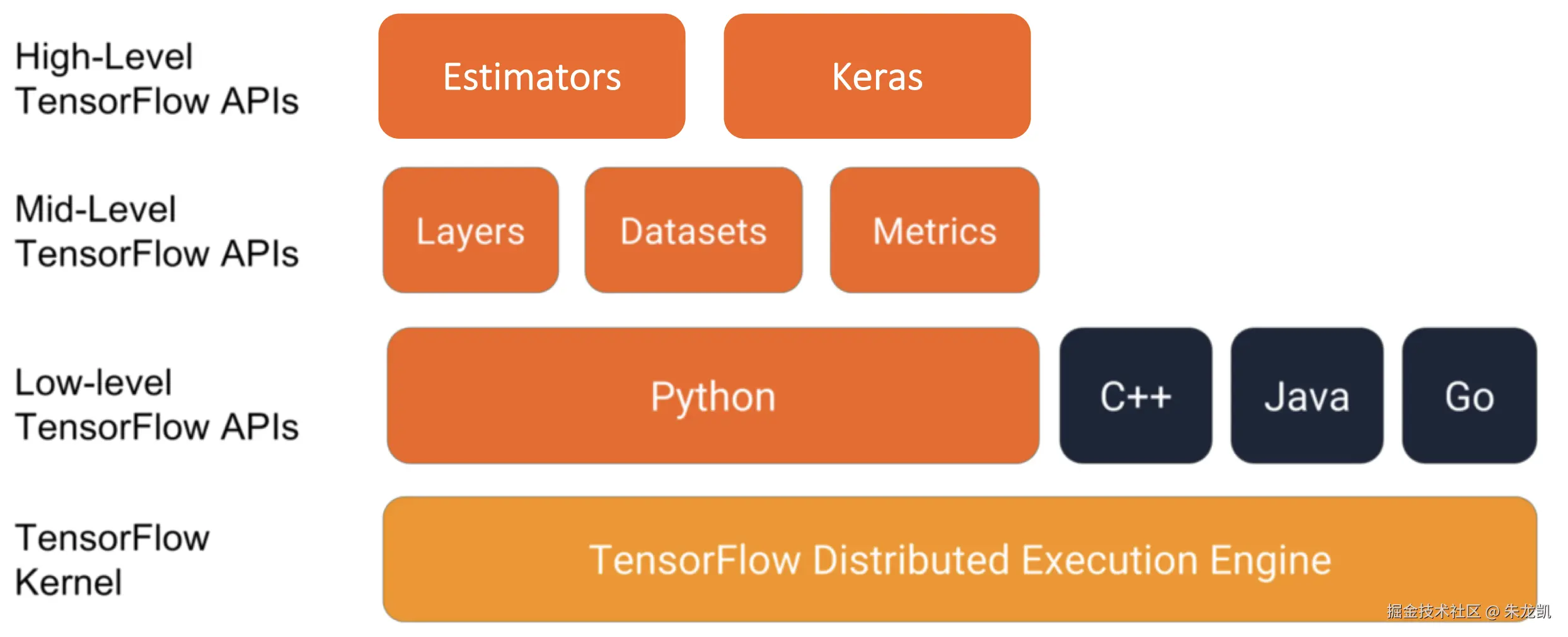
-
Estimator 封装了机器学习工作流中的许多细节,包括训练循环、评估循环、模型保存与导出等,旨在让用户能够快速构建、训练和部署模型,而无需关心底层的会话(Session)、图(Graph)和占位符(Placeholder)等细节。它非常适合生产环境和中等规模的标准模型。
-
Keras 用户友好,适合入门者学习,可以通过可配置的模块搭建模型。
-
layers 在神经网络中,层是一个数据处理模块,它接收一个或多个张量作为输入,并输出一个或多个张量。
-
Datasets 这是 TensorFlow 用于构建高效、复杂数据输入管道的官方方法,是训练模型时喂送数据的最佳实践。
架构
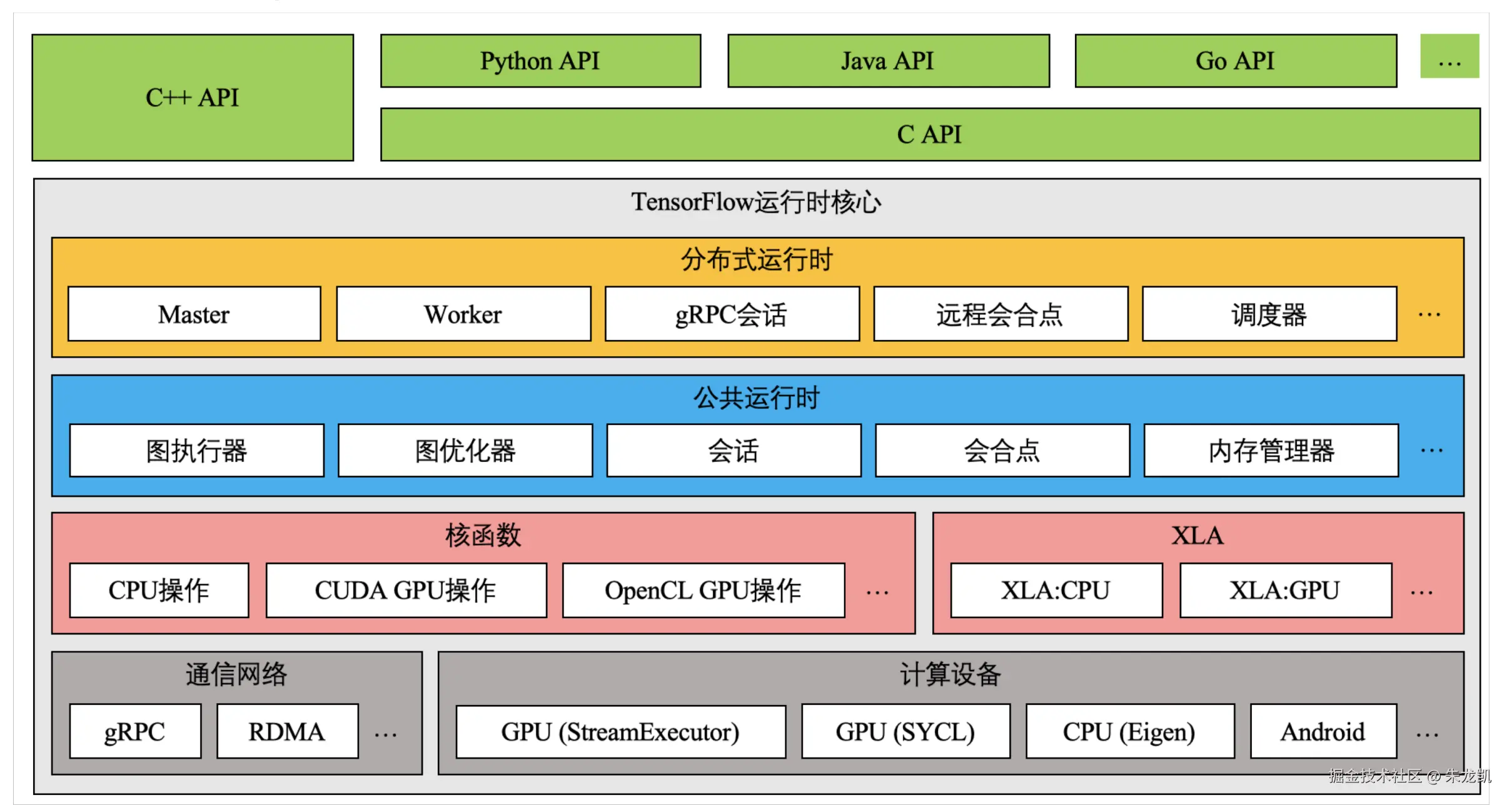
- 客户端层 (Client APIs)
Python API: 最常用,提供完整的功能和易用性
Java/Go API: 用于企业集成和移动端开发
C++ API: 高性能应用和嵌入式系统
C API: 跨语言接口,其他语言通过C API调用TensorFlow
- TensorFlow运行时核心 分布式运行时 (Distributed Runtime)
Master: 协调多个worker,管理计算图分区
Worker: 执行具体的计算任务
gRPC会话: 进程间通信,支持分布式训练
远程会合点: 协调跨设备的数据交换
调度器: 任务调度和资源分配
- 公共运行时 (Common Runtime)
会话(Session): 连接客户端和执行环境的桥梁
图执行器: 执行计算图的操作
图优化器: 优化计算图性能(如常量折叠、操作融合)
会合点: 协调操作之间的数据流
内存管理器: 管理设备内存分配和回收
- 计算设备层 (Compute Devices)
硬件加速器
CPU (Eigen): 使用Eigen库进行CPU优化计算
GPU (StreamExecutor): NVIDIA GPU加速计算
GPU (SYCL): 开放式标准,支持多种GPU厂商
Android: 移动设备优化
通信网络 gRPC: Google开发的远程过程调用,用于分布式通信
RDMA: 远程直接内存访问,高性能网络通信
- 编译器优化层
XLA (Accelerated Linear Algebra) XLA:CPU: 将计算图编译为优化的CPU代码
XLA:GPU: 生成高度优化的GPU代码
即时编译(JIT)和提前编译(AOT)支持
TensorFlow数据流图
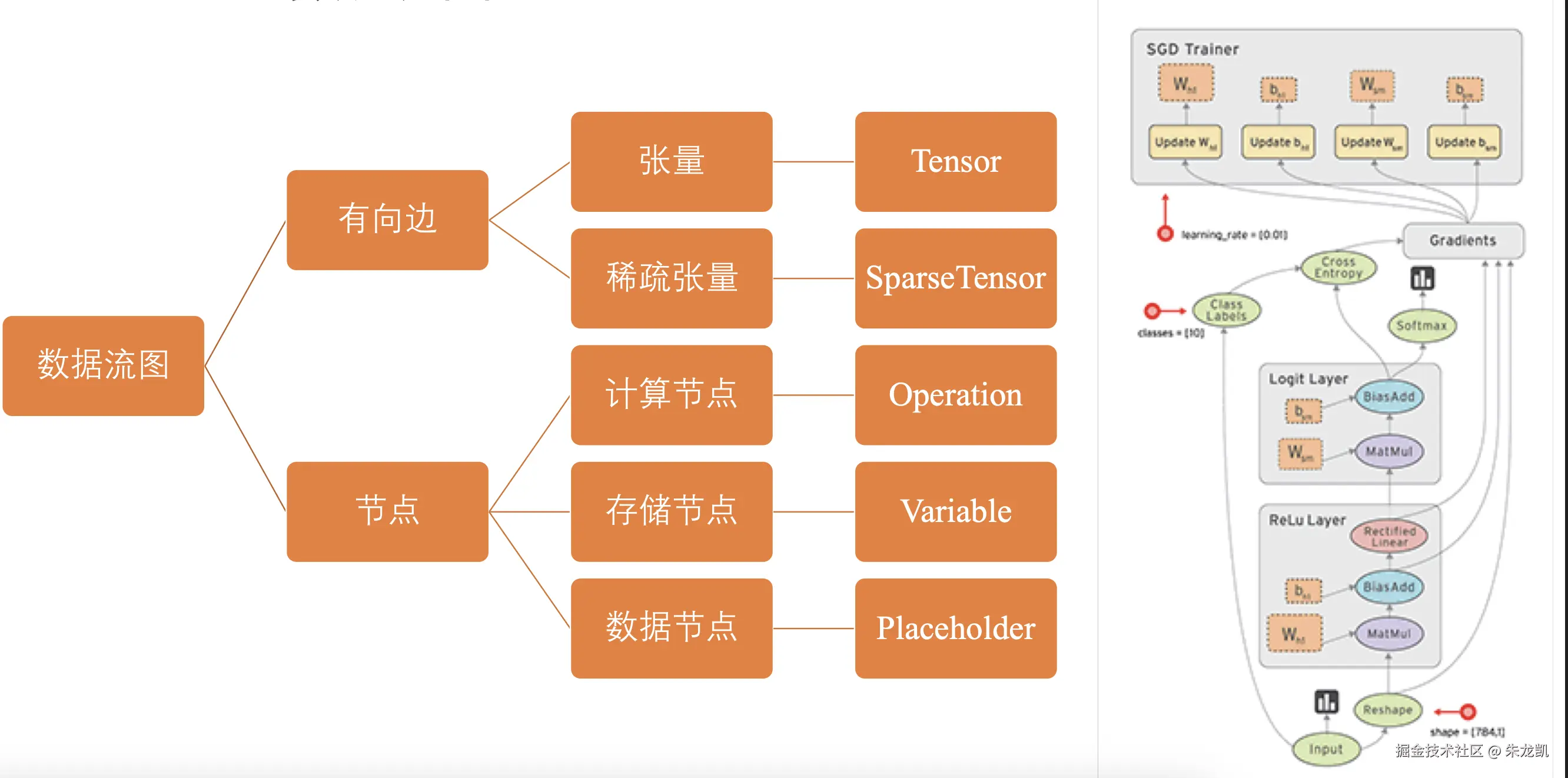
张量可以理解为变量,通常是一个矩阵,稀疏张量是那些高维矩阵,但是很多元素没有计算意义。数据节点对于输入数据进行表示。
在数据流图中,每一次训练从输入节点开始,数据从当前节点通过有向边流入下一个节点,整个计算过程就像一个队列中的元素,将入度为0的节点进行计算。
数据流图的优势是并行计算和分布式计算都很快,而且通过预编译计算能实现很多优化。
张量
表示某种相同数据类型的多维数据,有两个重要属性,数据类型和数组形状(每个维度的大小)。 常量,值不可变的张量,在创建时必须指定值;占位符,是一个空壳,不存储值,由外部输入决定,已经在版本2中废弃;变量,值可以改变的张量,通常用于存储模型参数。
变量
是一种特殊的张量,用于维护特定节点的状态,如模型参数的权重和参数,在下轮训练中仍然需要使用,需要通过变量维护在内存中。
变量的使用流程:
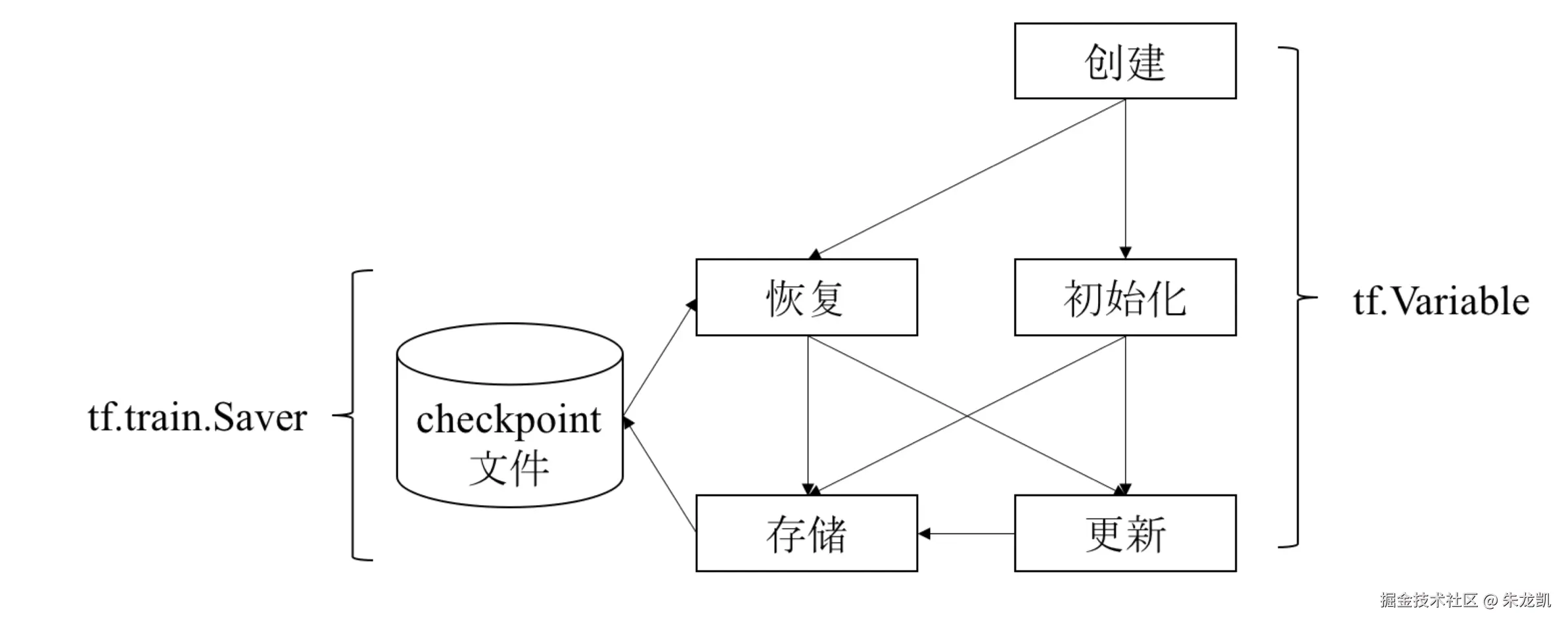 在加载数据流图后,需要初始化变量,这个时候可以将变量存储到chekcpoint文件中,也可以从中恢复出参数,继续更新模型参数。在训练过程中,也可以将已经训练好的的参数更新存储到文件中。
在加载数据流图后,需要初始化变量,这个时候可以将变量存储到chekcpoint文件中,也可以从中恢复出参数,继续更新模型参数。在训练过程中,也可以将已经训练好的的参数更新存储到文件中。
Saver使用实例:
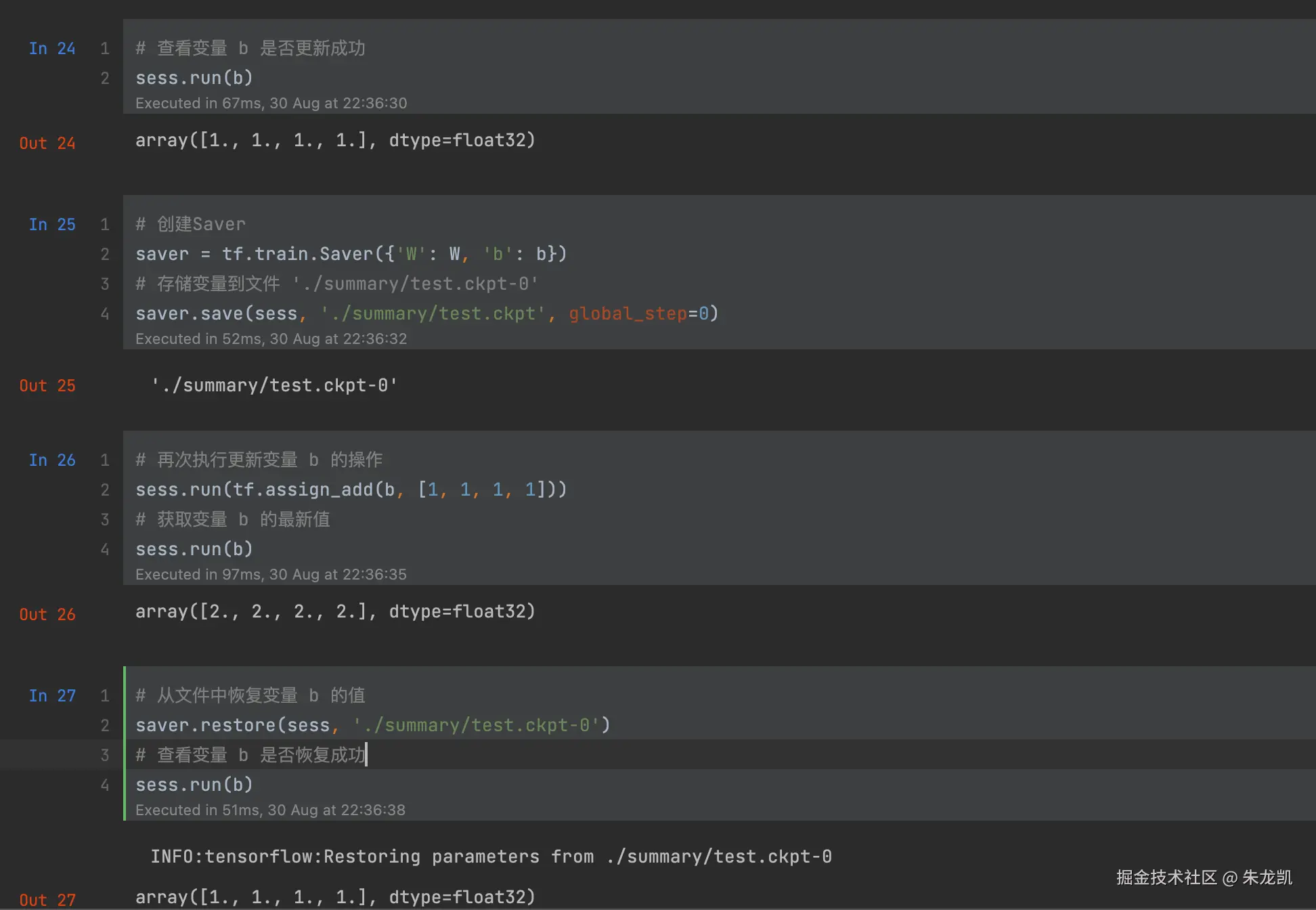
操作
TensorFlow用数据流图表示算法模型,数据流图由边和节点组成,每个节点均对应一个具体的操作。
计算和控制操作:

使用占位符操作表示图外的数据,如训练数据和测试数据。在用户向数据流图填充数据前,图中并没有执行任何计算。
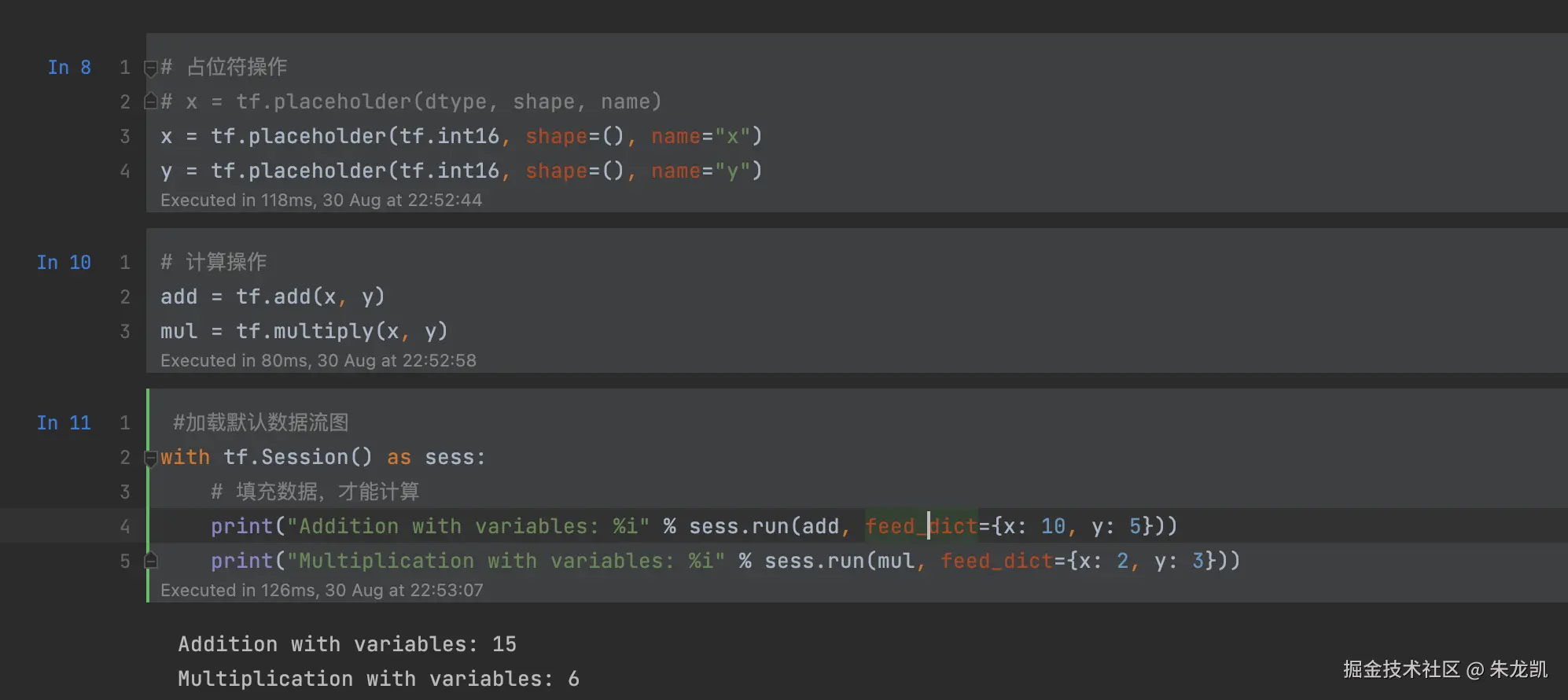
会话
会话提供了估算张量和执行运算的运行时环境,是发放任务的客户端,所有计算任务都由他连接执行引擎执行。
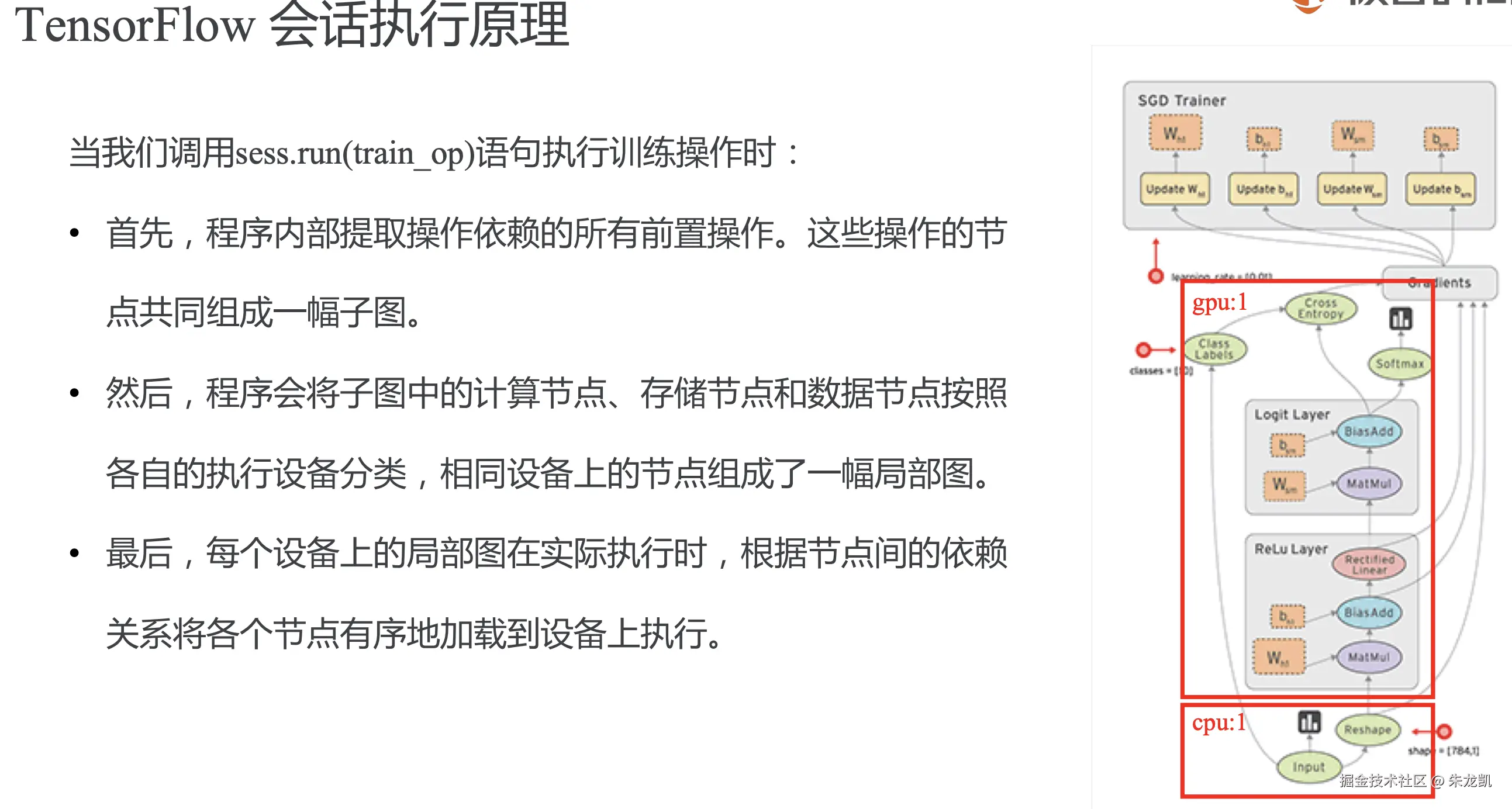
估算张量除了session.run()方法,还有如下两种:
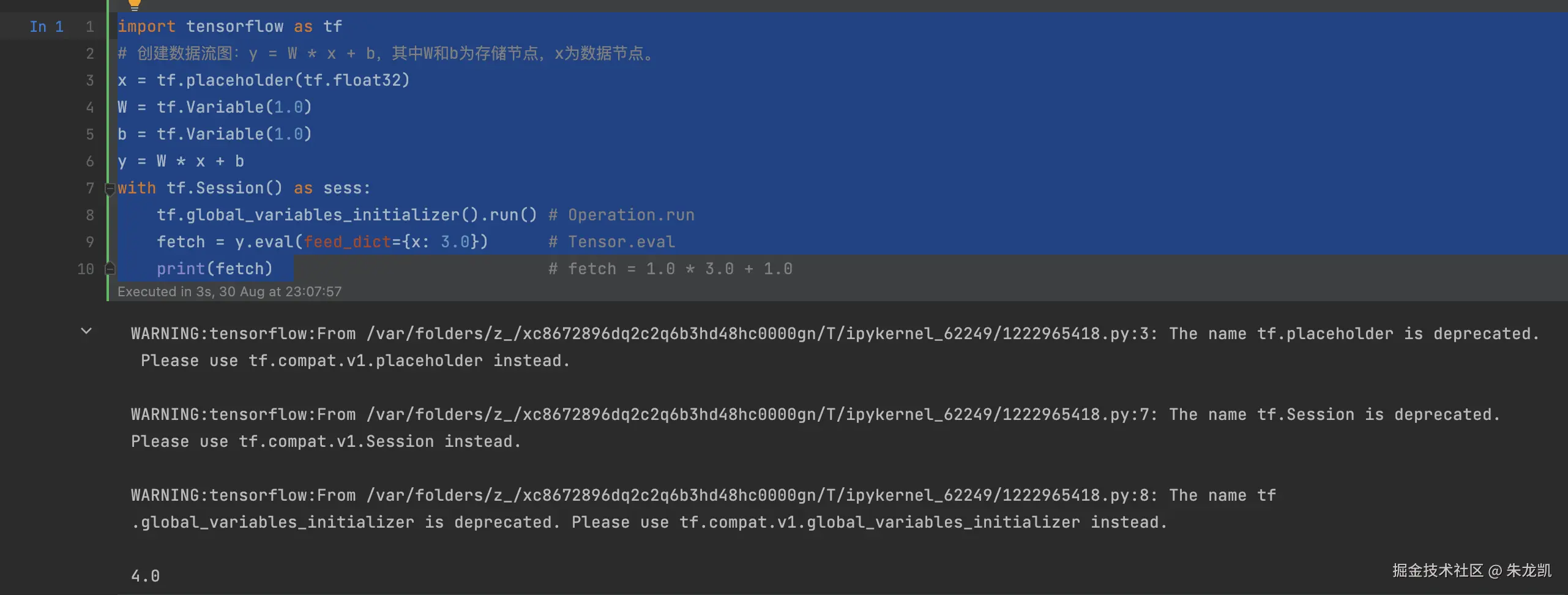 实际上以上两种估算张量最终实现方式也是通过会话实现:
实际上以上两种估算张量最终实现方式也是通过会话实现:
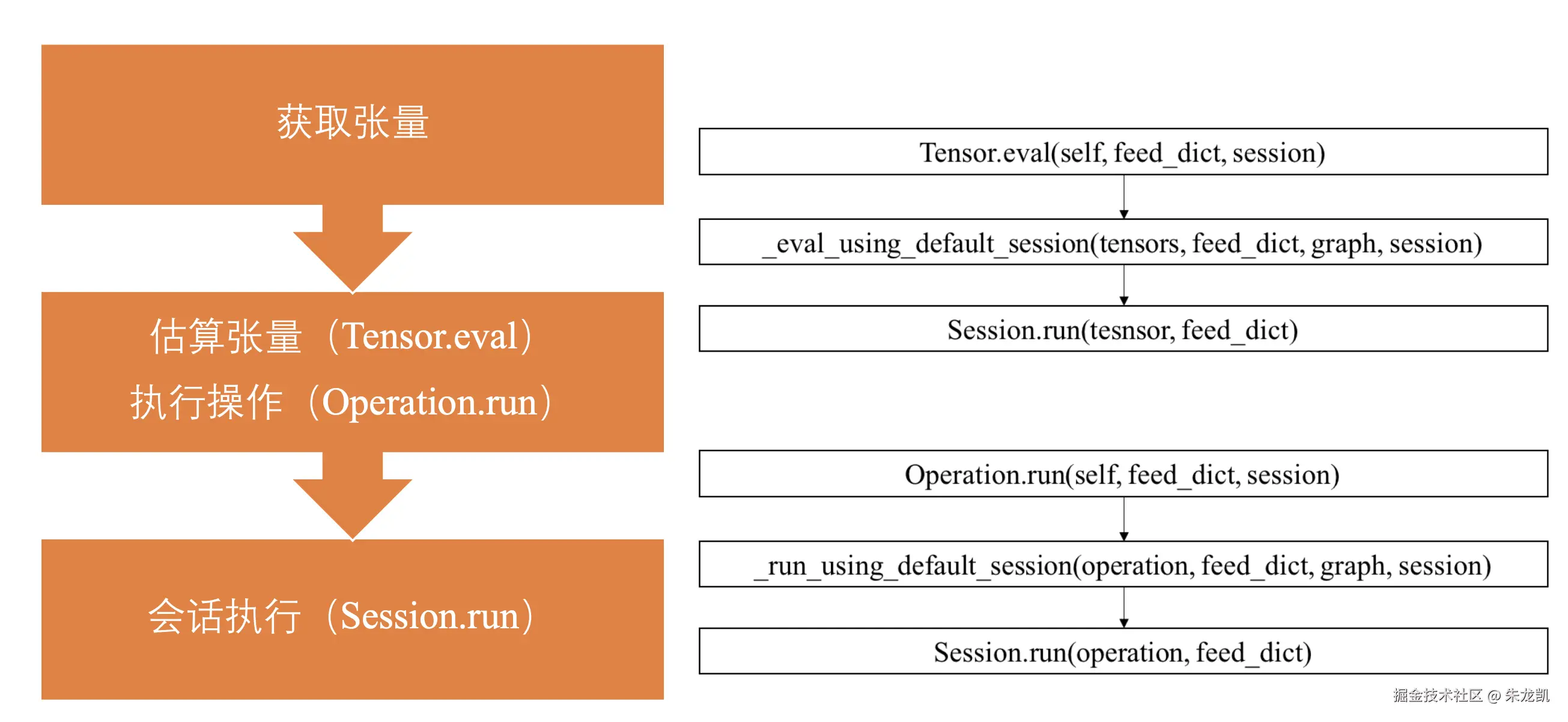
优化器
损失函数是评估特定模型参数与特点输入时,模型预测值与真实值之间的不一致程度的函数。 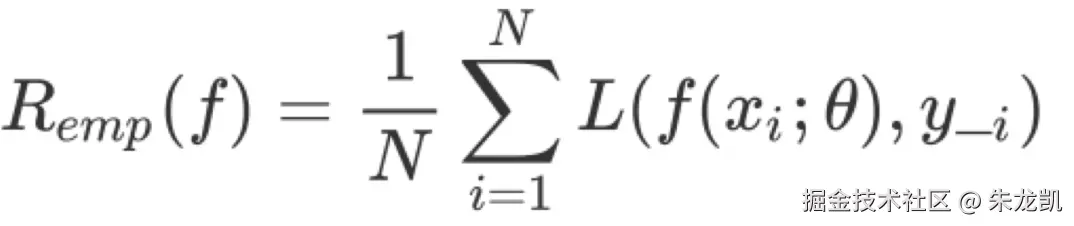 使用损失函数对所有训练样本求损失值,再累加计算平均值,得到经验风险。
使用损失函数对所有训练样本求损失值,再累加计算平均值,得到经验风险。
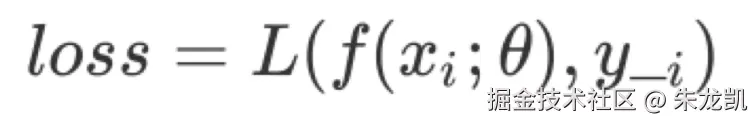 但是不能过度追求降低损失值,因为测试数据不能代表真实场景的数据分布,当两者分布不一致时,过度依赖测试数据会造成过拟合问题,导致模型泛化能力过差。
但是不能过度追求降低损失值,因为测试数据不能代表真实场景的数据分布,当两者分布不一致时,过度依赖测试数据会造成过拟合问题,导致模型泛化能力过差。
模型训练的目标是不断降低经验风险,但是随着训练步数增加,经验风险降低,模型复杂度在提高,为了降低过度训练造成模型复杂度提高,引入了专门度量模型复杂度的正则化项。
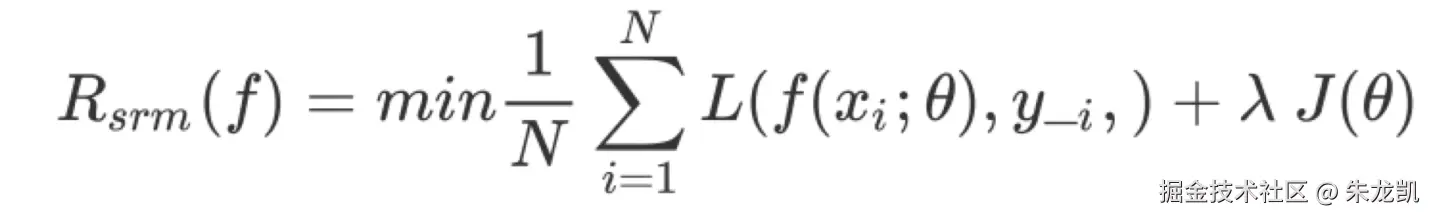
典型的机器学习问题和深度学习问题通常都需要转化为最优化问题求解。优化算法通常采用迭代的方式实现,首先设定一个可行解,然后基于特定的函数反复重复计算可行解,直到找到一个最优解或者达到预设的收敛条件。
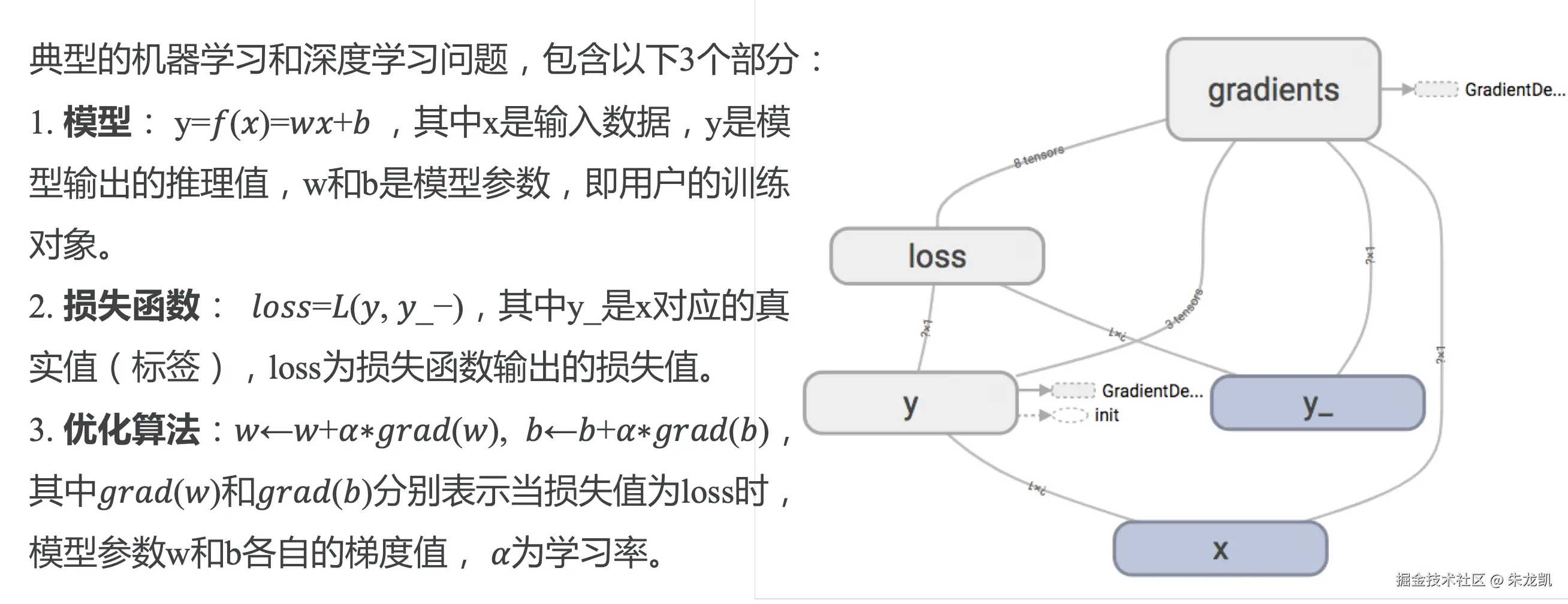
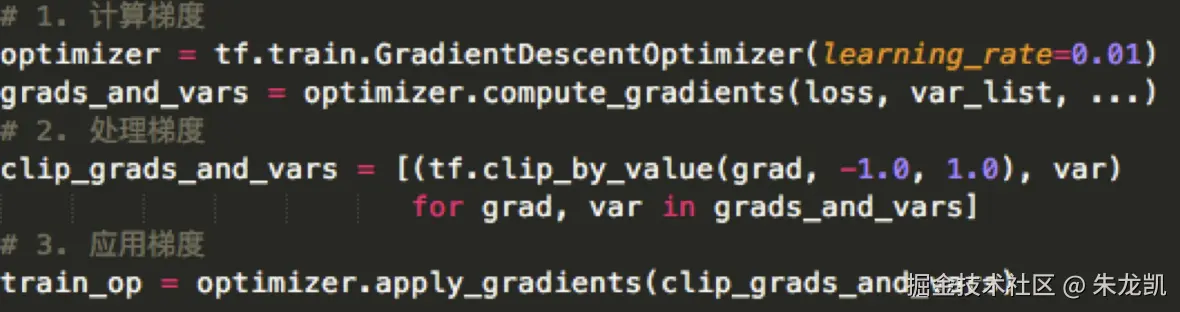
一次典型的优化分为三个步骤:
- 计算梯度;
- 按照需求处理梯度,如梯度裁剪和梯度加权;
- 应用梯度,将处理后的梯度值应用到模型参数;
房价预测模型实战
监督学习
指训练数据是包括输入和预期输出的,通过这些数据学习得到一个模型,然后可以根据新的输入推测出结果的方法。
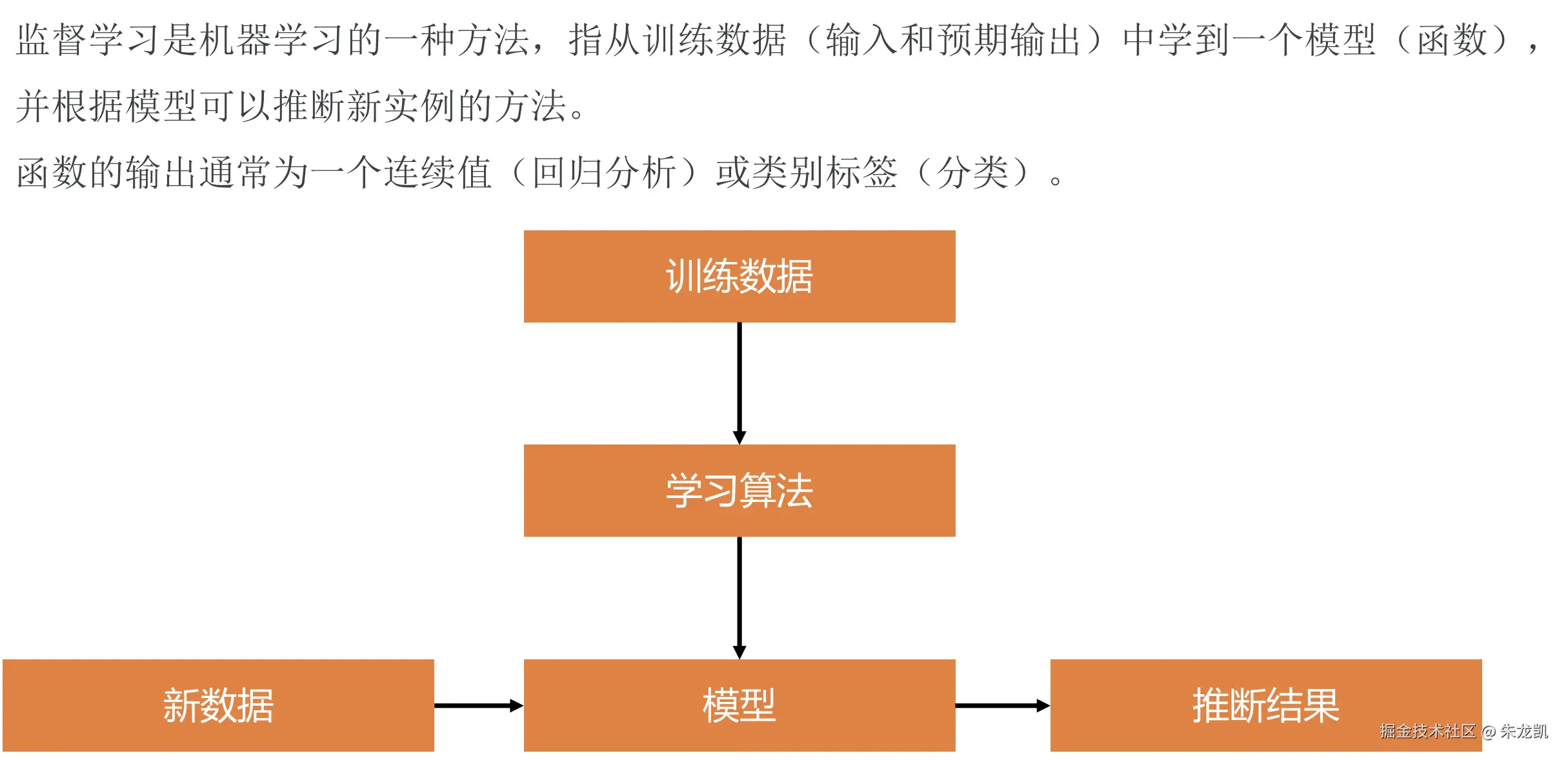 经典监督学习算法
经典监督学习算法
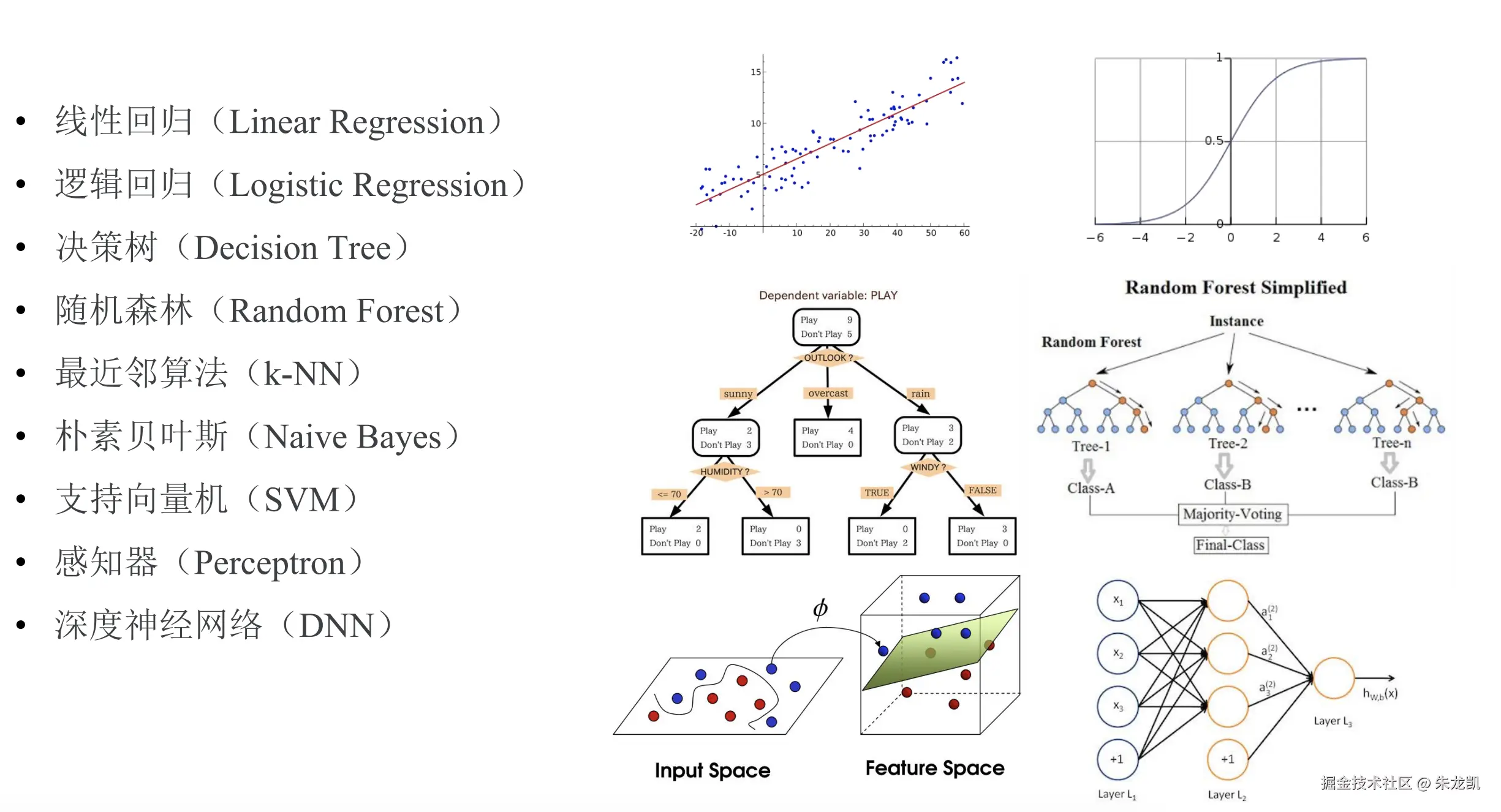
梯度下降:
整个模型迭代的过程中是为了优化损失函数达到最小,这个过程可以理解下山的过程中,需要不断寻找最陡峭的方向前进,这样在固定步长的情况下,下降高度是最快的,能够更快到达山底。 梯度:函数在某点变化最快的方向;


数据处理
下面是价格随面积变化的训练数据:
python
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
sns.set(context="notebook", style="whitegrid", palette="dark")
df0 = pd.read_csv('data0.csv', names=['square', 'price'])
# 使用关键字参数
sns.lmplot(x='square', y='price', data=df0, height=6, fit_reg=True)
plt.show()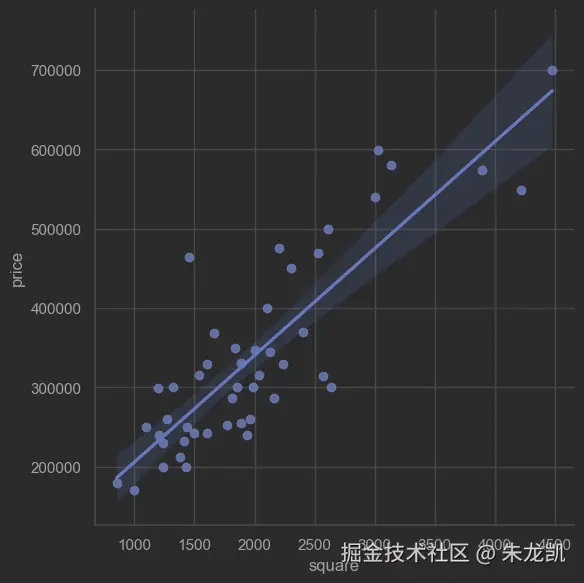 以上是原始房价数据使用线形关系可视化后的图。
以上是原始房价数据使用线形关系可视化后的图。
下面是价格随面积、房间数变化的数据,首先对房价数据进行处理:
css
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
df1 = pd.read_csv('data1.csv', names=['square', 'bedrooms', 'price'])
df1.head()
def normalize_feature(df):
return df.apply(lambda column: (column - column.mean()) / column.std())
df = normalize_feature(df1)
df.head()
ax = plt.axes(projection='3d')
ax.set_xlabel('square')
ax.set_ylabel('bedrooms')
ax.set_zlabel('price')
ax.scatter3D(df['square'], df['bedrooms'], df['price'], c=df['price'], cmap='Reds')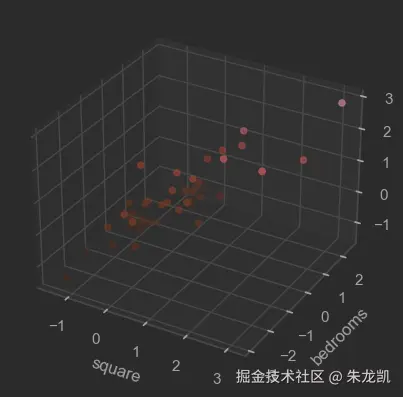
需要添加一个全一的列:
ini
import numpy as np
ones = pd.DataFrame({'ones': np.ones(len(df))})# ones是n行1列的数据框,表示x0恒为1
df = pd.concat([ones, df], axis=1) # 根据列合并数据
df.head()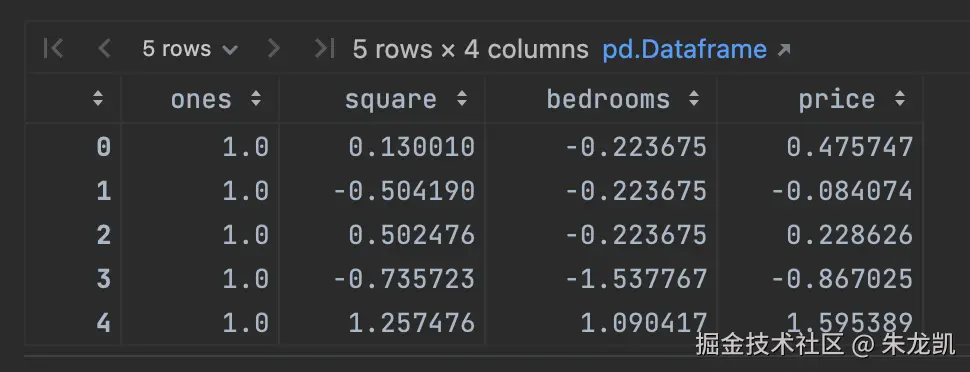
创建线形回归模型(数据流图)
ini
import pandas as pd
import numpy as np
def normalize_feature(df):
return df.apply(lambda column: (column - column.mean()) / column.std())
# 对特征进行处理
df = normalize_feature(pd.read_csv('data1.csv',
names=['square', 'bedrooms', 'price']))
# 添加全1列,为了可以将变量和参数做矩阵乘法
ones = pd.DataFrame({'ones': np.ones(len(df))})# ones是n行1列的数据框,表示x0恒为1
df = pd.concat([ones, df], axis=1) # 根据列合并数据
df.head()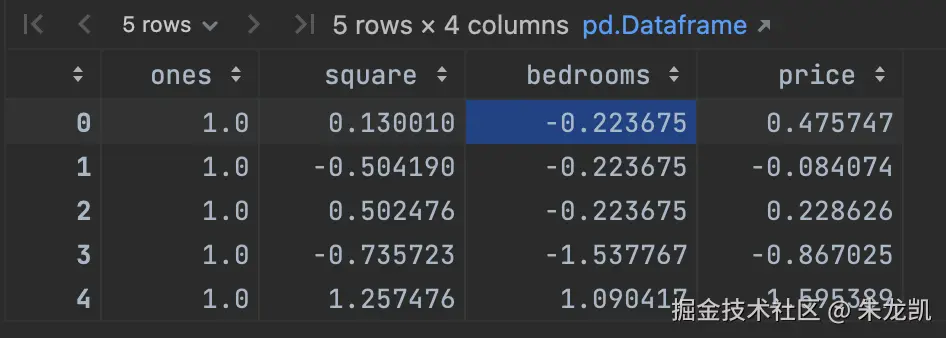
bash
# 数据前三列为输入测试参数
X_data = np.array(df[df.columns[0:3]])
# 最后一列为房价,训练数据的结果数据
y_data = np.array(df[df.columns[-1]]).reshape(len(df), 1)
print(X_data.shape, type(X_data))
print(y_data.shape, type(y_data))
ini
import tensorflow as tf
import numpy as np
alpha = 0.01 # 学习率 alpha
epoch = 500 # 训练全量数据集的轮数
# 初始化权重,和输入参数列数一致
W = tf.Variable(tf.zeros((X_data.shape[1], 1)), name='weights')
# 优化器,随机梯度下降
optimizer = tf.keras.optimizers.SGD(learning_rate=alpha)
# 训练循环
for e in range(1, epoch + 1):
# 是 GradientTape是TensorFlow 2.x 中的自动微分工具,用于计算函数的梯度(导数)
with tf.GradientTape() as tape:
# 前向传播,matmul用于执行两个矩阵的乘法运算
y_pred = tf.matmul(X_data.astype(np.float32), W)
# 计算损失
loss = tf.reduce_mean(tf.square(y_pred - y_data)) / 2
# 计算梯度
gradients = tape.gradient(loss, [W])
# 更新权重
optimizer.apply_gradients(zip(gradients, [W]))
if e % 10 == 0:
W_np = W.numpy()
log_str = "Epoch %d \t Loss=%.4g \t Model: y = %.4gx1 + %.4gx2 + %.4g"
print(log_str % (e, loss.numpy(), W_np[1][0], W_np[2][0], W_np[0][0]))
print("\n训练完成!")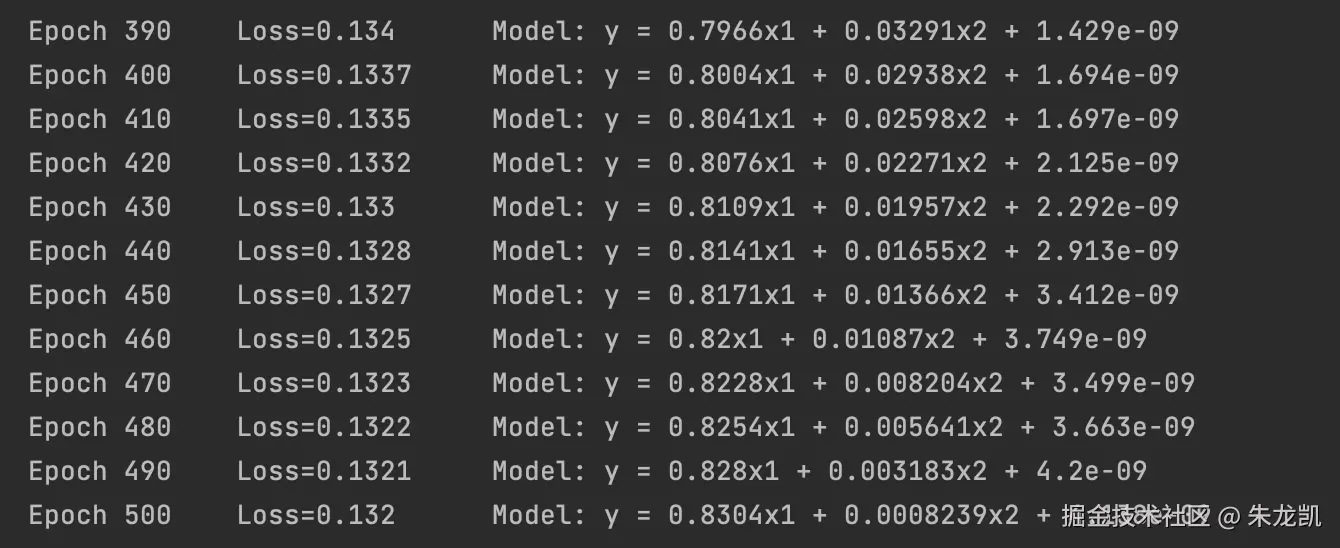
可视化数据流图
 可视化数据流图的过程:
可视化数据流图的过程:
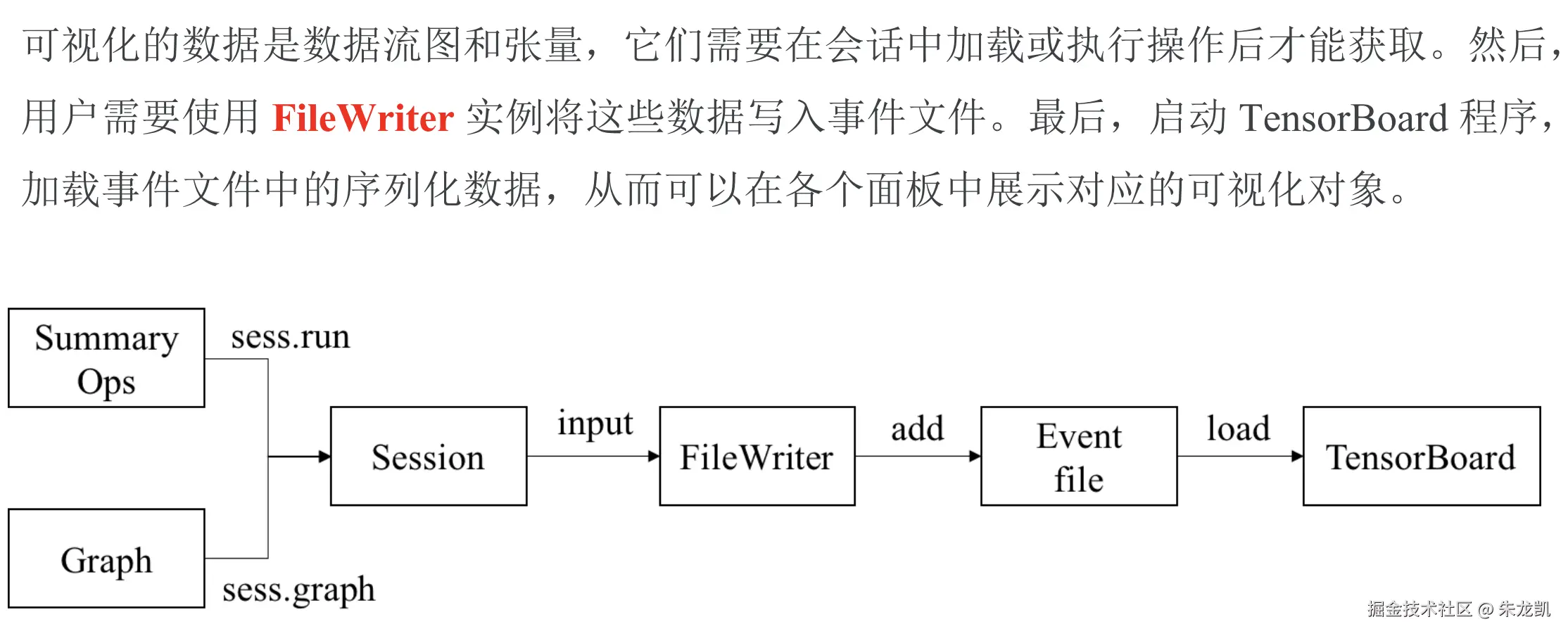 以下是房屋价格预测数据流图的代码:
以下是房屋价格预测数据流图的代码:
ini
import pandas as pd
import numpy as np
import tensorflow as tf
import os
def normalize_feature(df):
return df.apply(lambda column: (column - column.mean()) / column.std())
df = normalize_feature(pd.read_csv('data1.csv',
names=['square', 'bedrooms', 'price']))
ones = pd.DataFrame({'ones': np.ones(len(df))})
df = pd.concat([ones, df], axis=1)
X_data = np.array(df[df.columns[0:3]])
y_data = np.array(df[df.columns[-1]]).reshape(len(df), 1)
alpha = 0.01
epoch = 500
# 清除日志目录
log_dir = './summary/linear-regression-1'
if os.path.exists(log_dir):
import shutil
shutil.rmtree(log_dir)
# 使用 tf.compat.v1 来保持TensorFlow 1.x的兼容性
tf.compat.v1.disable_eager_execution() # 关闭即时执行模式
with tf.compat.v1.Session() as sess:
with tf.name_scope('input'):
X = tf.compat.v1.placeholder(tf.float32, X_data.shape, name='X')
y = tf.compat.v1.placeholder(tf.float32, y_data.shape, name='y')
with tf.name_scope('hypothesis'):
W = tf.compat.v1.get_variable("weights",
(X_data.shape[1], 1),
initializer=tf.compat.v1.constant_initializer())
y_pred = tf.matmul(X, W, name='y_pred')
with tf.name_scope('loss'):
loss_op = 1 / (2 * len(X_data)) * tf.matmul((y_pred - y), (y_pred - y), transpose_a=True)
with tf.name_scope('train'):
train_op = tf.compat.v1.train.GradientDescentOptimizer(learning_rate=alpha).minimize(loss_op)
# 初始化变量
sess.run(tf.compat.v1.global_variables_initializer())
# 创建FileWriter并写入计算图
writer = tf.compat.v1.summary.FileWriter(log_dir, sess.graph)
# 训练循环
for e in range(1, epoch + 1):
sess.run(train_op, feed_dict={X: X_data, y: y_data})
if e % 10 == 0:
loss, w = sess.run([loss_op, W], feed_dict={X: X_data, y: y_data})
log_str = "Epoch %d \t Loss=%.4g \t Model: y = %.4gx1 + %.4gx2 + %.4g"
print(log_str % (e, loss[0][0], w[1][0], w[2][0], w[0][0]))
writer.close()
print("训练完成!")
print("使用以下命令查看TensorBoard:")
print("tensorboard --logdir=./summary/linear-regression-1")数据流图可视化:
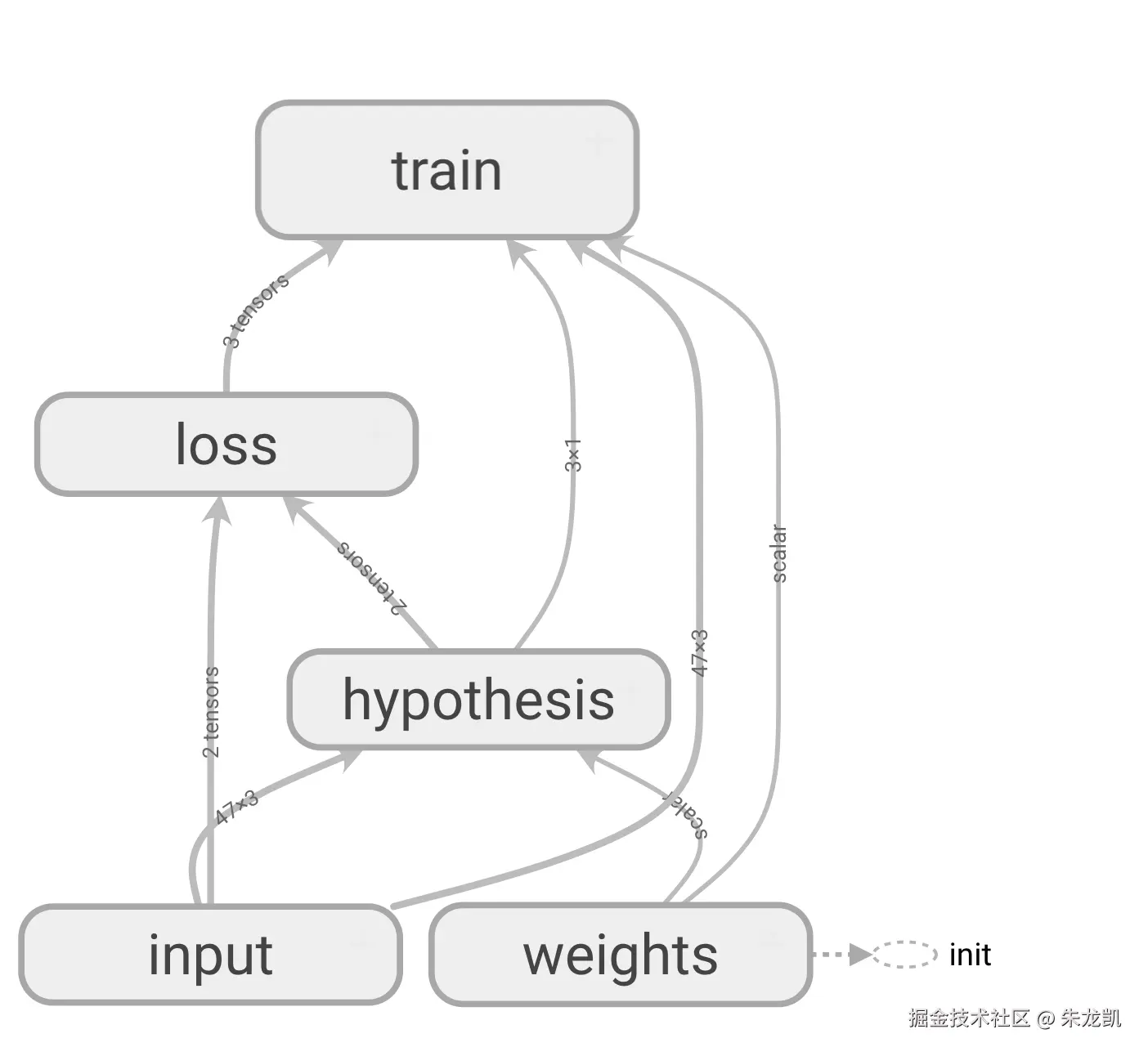
实战手写体数字识别
手写体数据集是一个图像集合,每张图片28*28像素。
scss
from keras.datasets import mnist
import matplotlib.pyplot as plt
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# print(x_train.shape, y_train.shape)
# print(x_test.shape, y_test.shape)
flg = plt.figure()
for i in range(15):
plt.subplot(3, 5, i+1)
plt.tight_layout()
plt.imshow(x_train[i], cmap='Grays')
plt.title('label:{}'.format(y_train[i]))
plt.xticks([])
plt.yticks([])
神经网络
神经网络是模拟生物神经结构和功能的数学模型或者计算模型,用于对函数进行估计或者近似。神经网络是多次神经元的连接,上一层的输出作为下一层的输入。
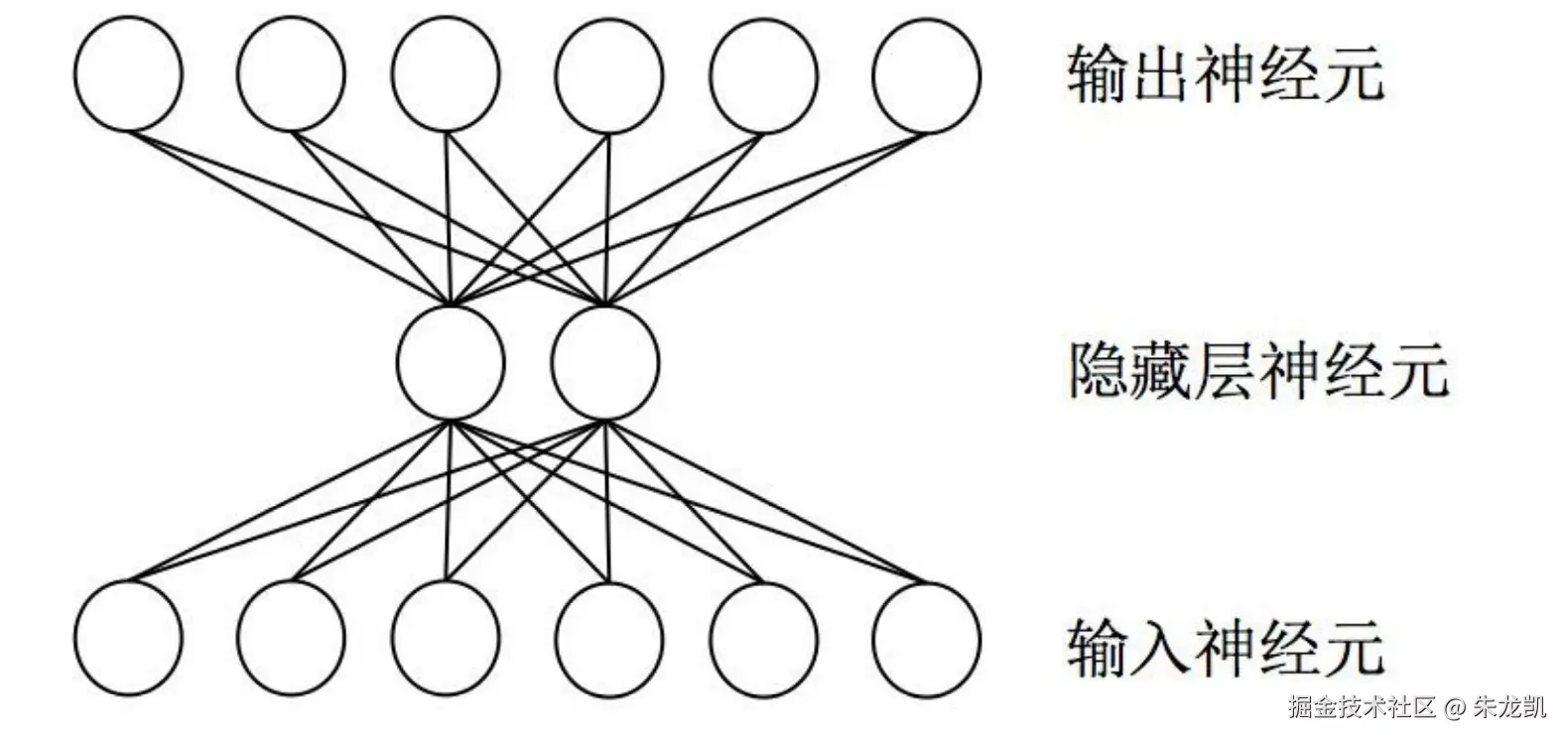
前向传播
将上一层的输出作为下一层的输入,并计算下一层的输出,一直到运算到输出层为止。
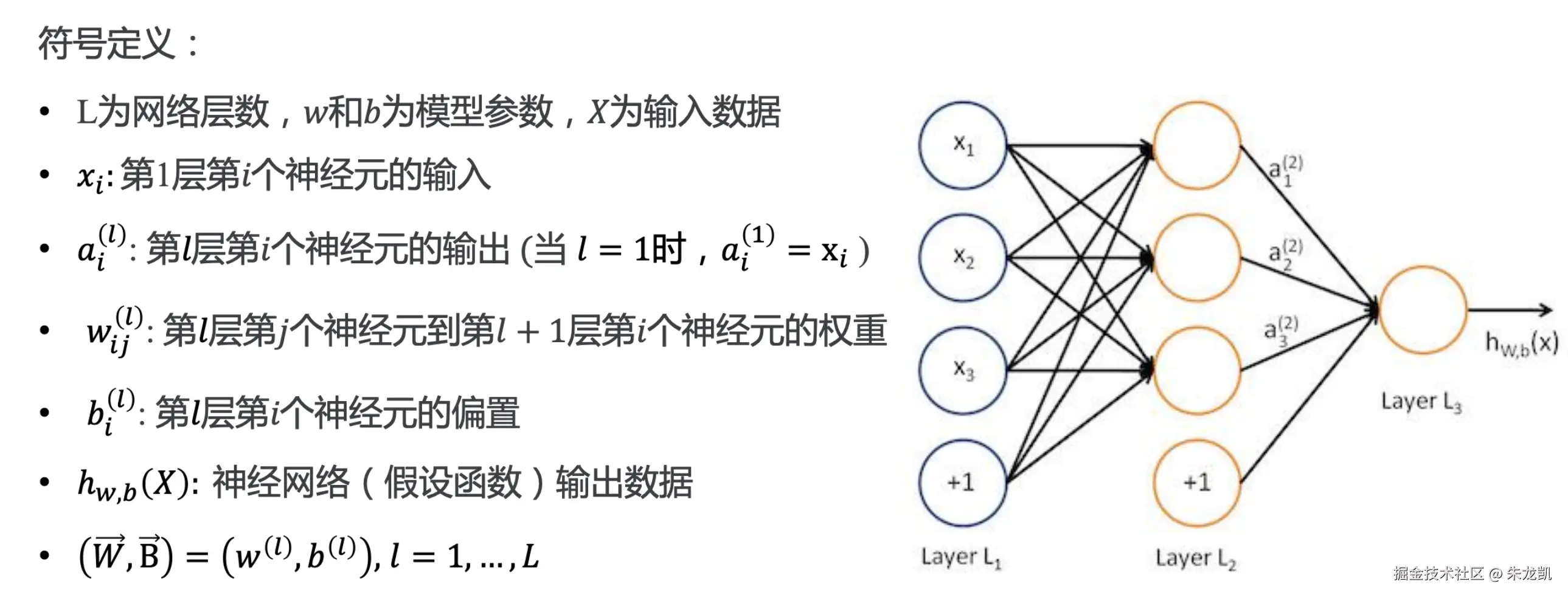
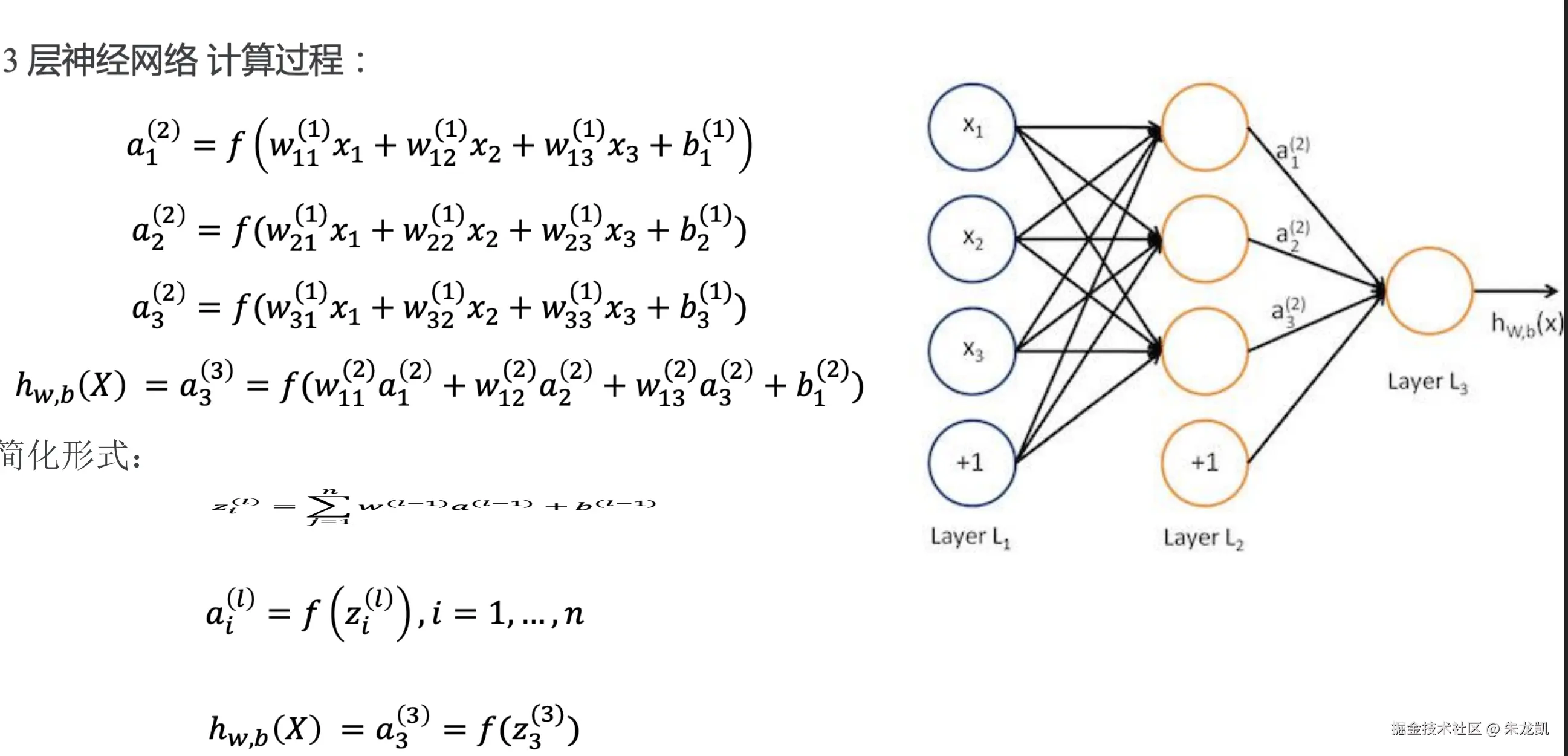
反向传播
反向传播仅指用于计算梯度的方法。反向传播算法的核心是代价函数 对网络中参数(各层的权重 和偏置 )的偏导表达式 。这些表达式描述了代价函数值 随权重 或偏置 变化而变化的程度。BP算法的简单理解:如果当前代价函数值距离预期值较远,那么我们通过调整权重 或偏置 的值使新的代价函数值更接近预期值(和预期值相差越大,则权重 或偏置 调整的幅度就越大)。一直重复该过程,直到最终的代价函数值在误差范围内,则算法停止。
Softmax网络训练
scss
from keras.datasets import mnist
import numpy as np
import matplotlib.pyplot as plt
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# 将图像本身从[28,28]转换为[784,]
X_train = x_train.reshape(60000, 784)
X_test = x_test.reshape(10000, 784)
# 将数据类型转换为float32
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
# 数据归一化
X_train /= 255
X_test /= 255
fig = plt.figure()
plt.bar(label, count, width = 0.7, align='center')
plt.title("Label Distribution")
plt.xlabel("Label")
plt.ylabel("Count")
plt.xticks(label)
plt.ylim(0,7500)
for a,b in zip(label, count):
plt.text(a, b, '%d' % b, ha='center', va='bottom',fontsize=10)
plt.show()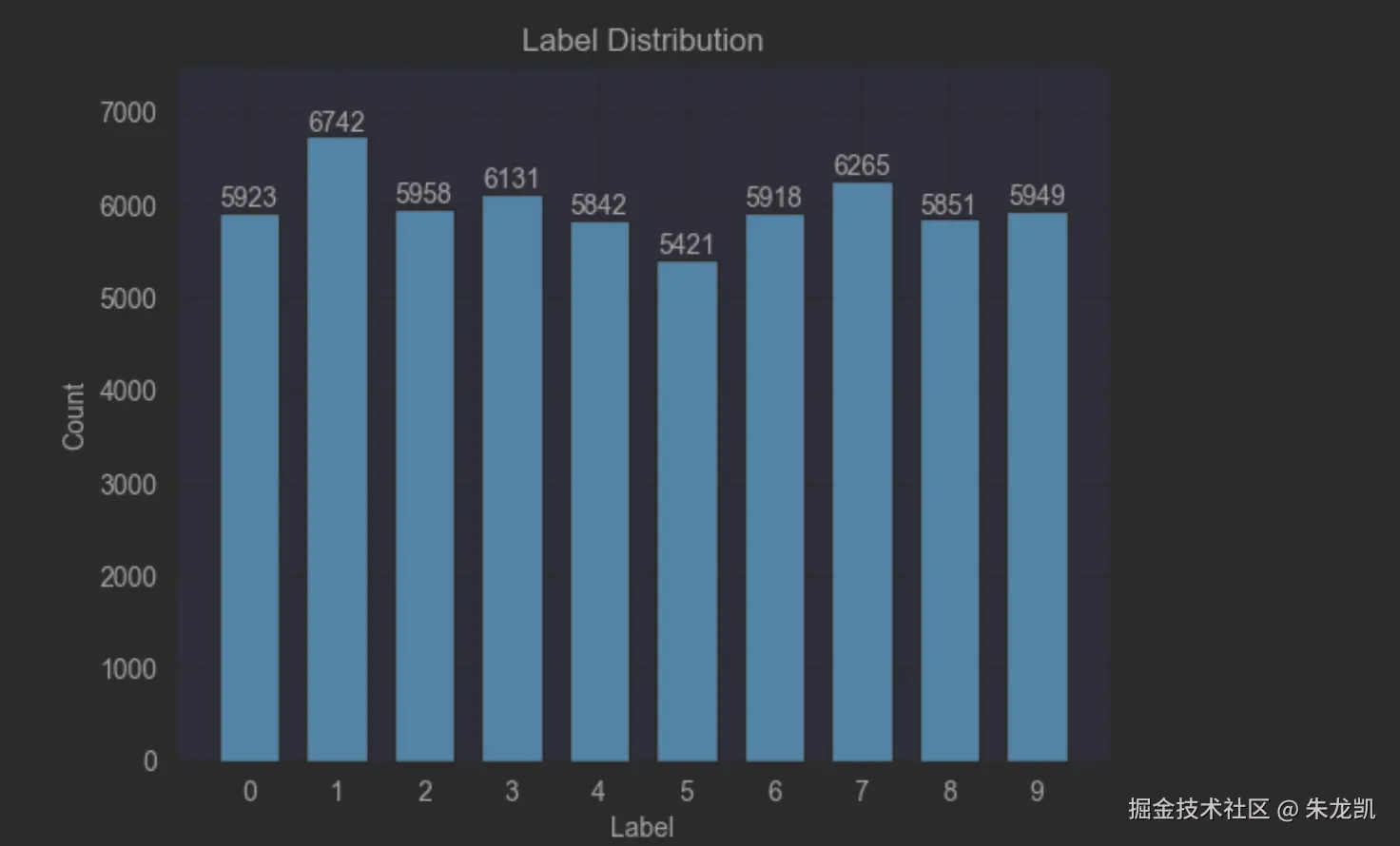
对数据进行one-hot处理:
ini
n_classes = 10
print("Shape before one-hot encoding: ", y_train.shape)
Y_train = tf.one_hot(y_train, depth=n_classes)
Y_test = tf.one_hot(y_test, depth=n_classes)
print(y_train[0])
print(Y_train[0])
ini
from keras.models import Sequential
from keras.layers import Dense, Activation # 直接从layers导入,不要core
model = Sequential()
model.add(Dense(512, input_shape=(784,)))
model.add(Activation('relu'))
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dense(10))
model.add(Activation('softmax'))
model.compile(loss='categorical_crossentropy', metrics=['accuracy'], optimizer='adam')
history = model.fit(X_train,
Y_train,
batch_size=128,
epochs=5,
verbose=2,
validation_data=(X_test, Y_test))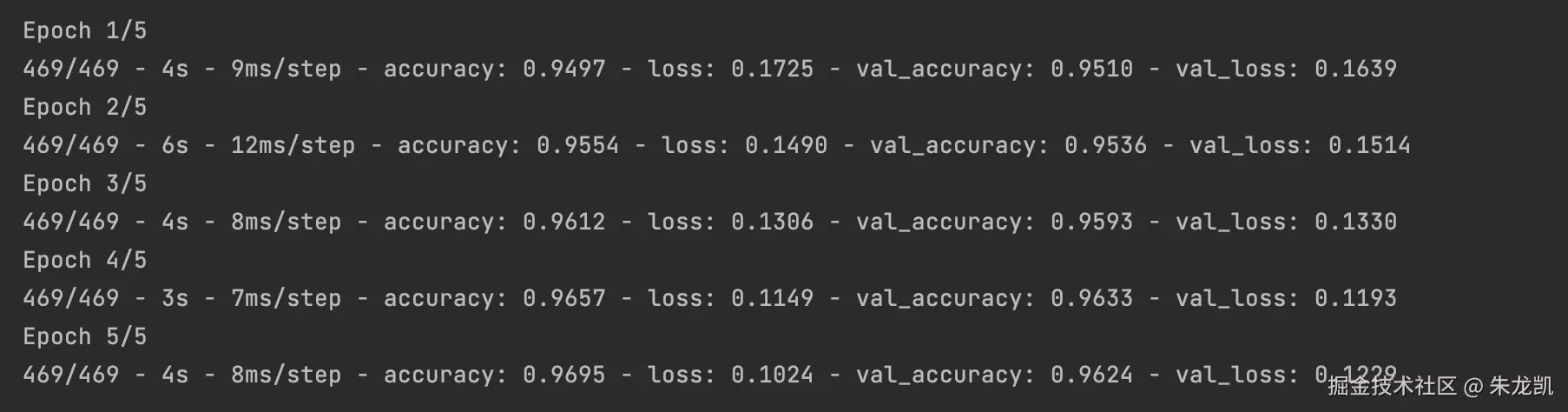
matlab
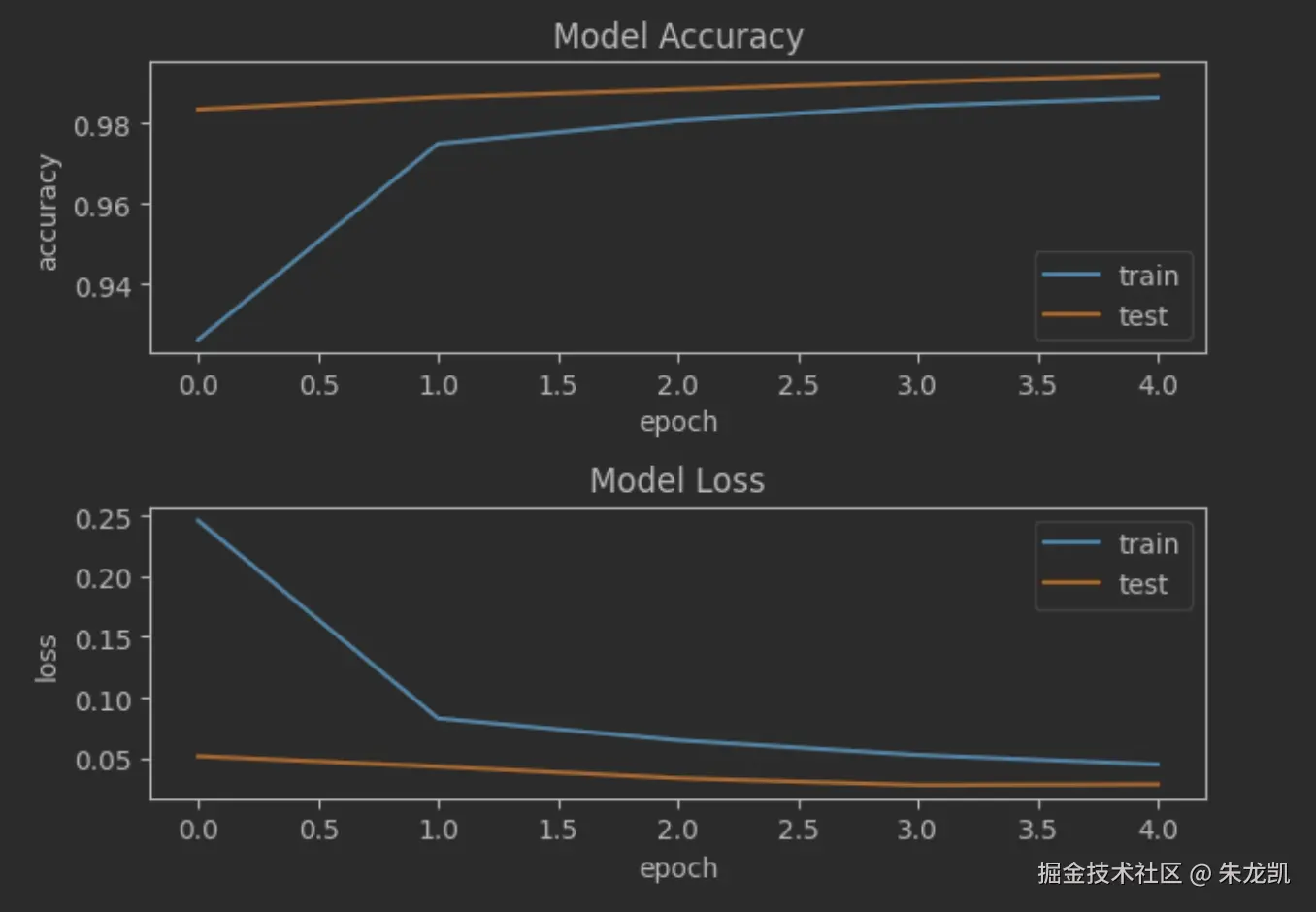
fig = plt.figure()
plt.subplot(2,1,1)
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.title('Model Accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='lower right')
plt.subplot(2,1,2)
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('Model Loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper right')
plt.tight_layout()
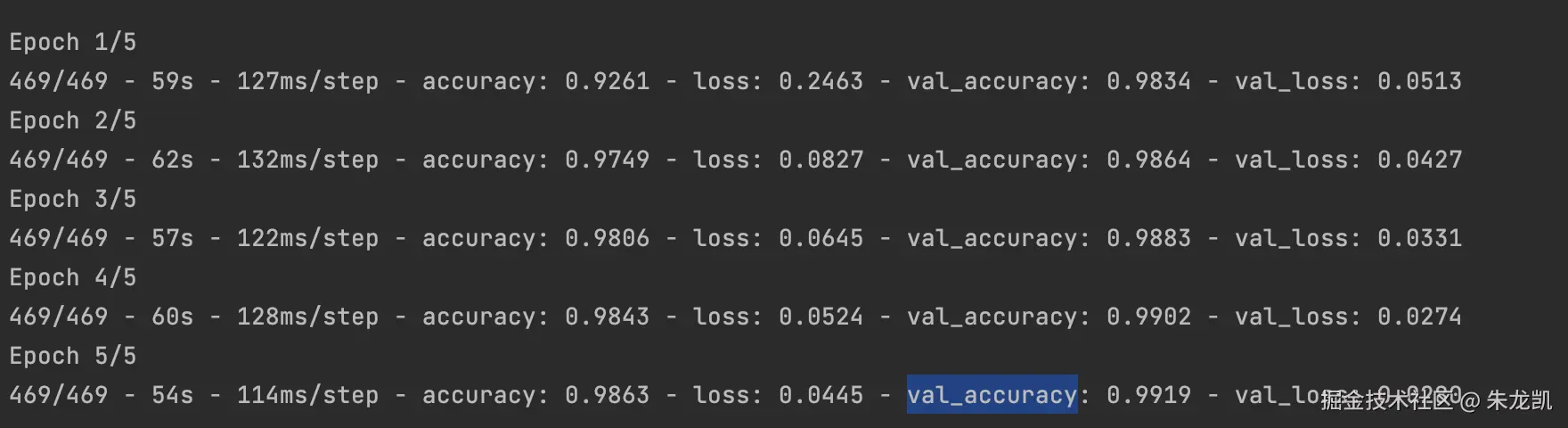
plt.show()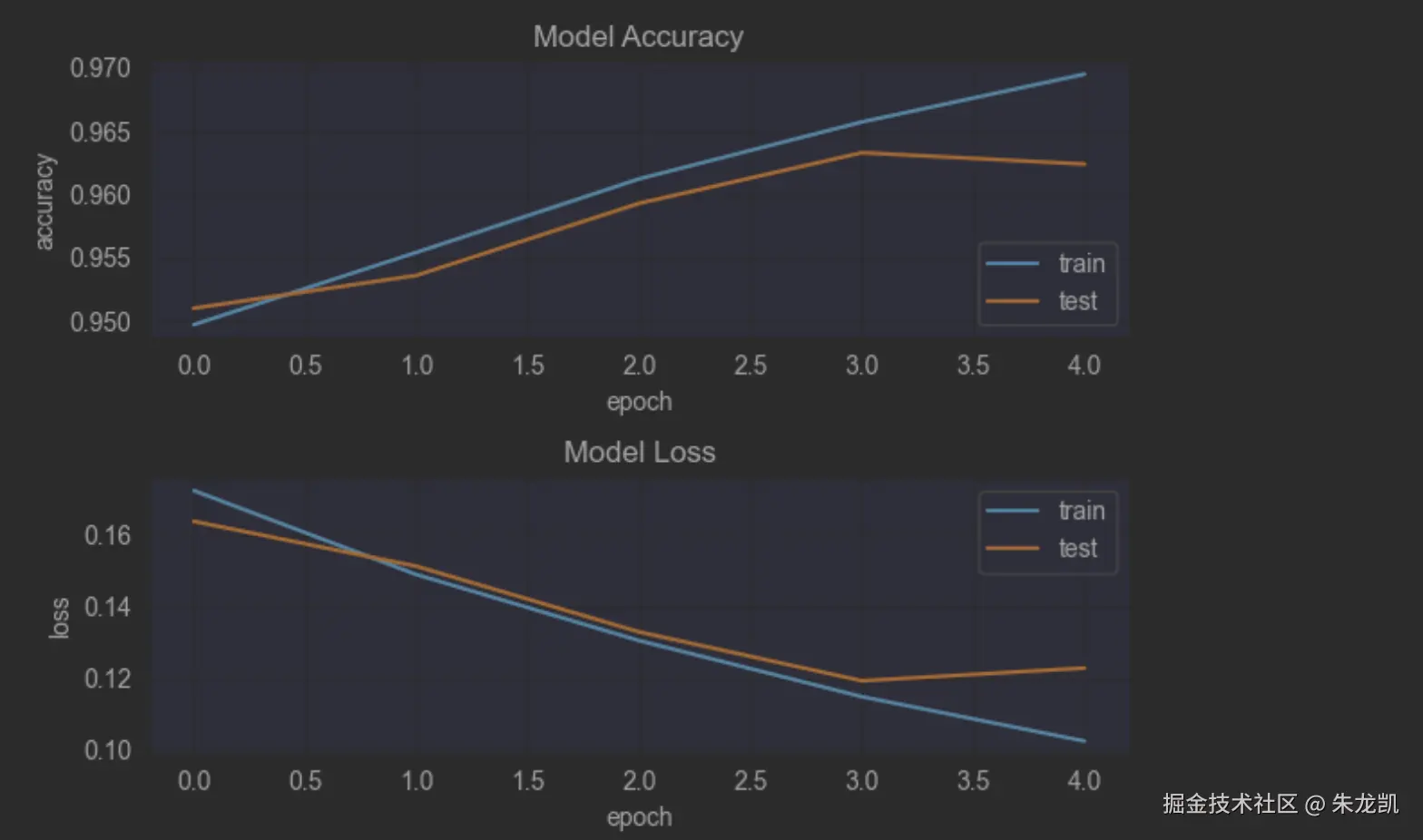 20轮的效果:
20轮的效果:
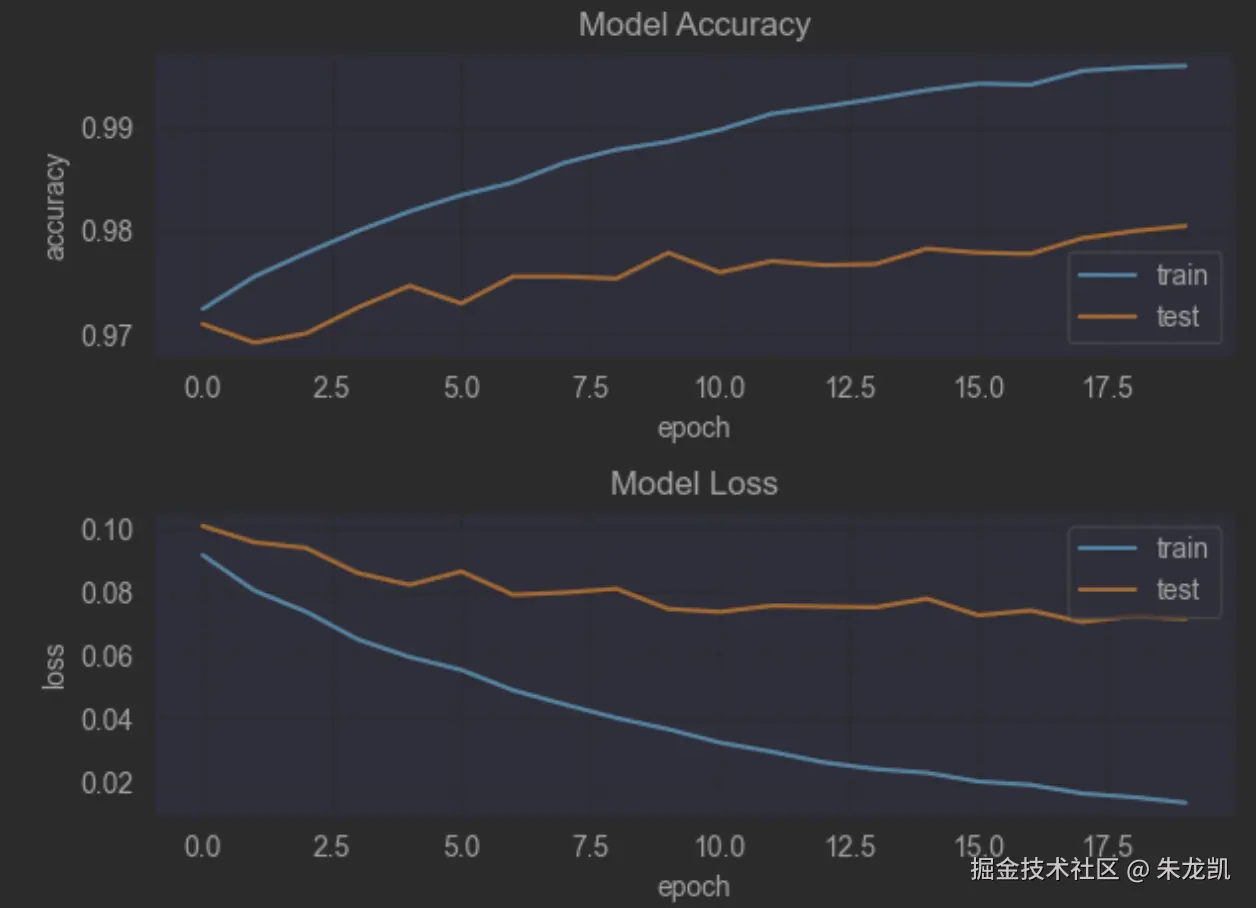
CNN网络
CNN(convolutional neural network),是一种以卷积为核心的前馈神经网络。关键思想:
- 局部感知,一个神经元不需要看全局,只需要看一小块,防止参数过多导致过拟合。
- 权重共享
卷积层
通过一系列卷积核与多通道输入数据做卷积运算,达到提取特征的目的;
池化层
在一个区域数据上进行采样,目的是缩小特征空间。有最大池化和平均池化。
Dropout层
核心思想是在训练过程中随机丢弃一些神经元,将神经元的输出置为0,防止参数过多,导致过拟合风险。
ini
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
model = Sequential()
## Feature Extraction
# 第1层卷积,32个3x3的卷积核,每个卷积核独立运用在输入上 ,激活函数使用 relu
model.add(Conv2D(filters=32, kernel_size=(3, 3), activation='relu',
input_shape=input_shape))
# 第2层卷积,64个3x3的卷积核,激活函数使用 relu
model.add(Conv2D(filters=64, kernel_size=(3, 3), activation='relu'))
# 最大池化层,池化窗口 2x2
model.add(MaxPooling2D(pool_size=(2, 2)))
# Dropout 25% 的输入神经元
model.add(Dropout(0.25))
# 将 Pooled feature map 摊平后输入全连接网络
model.add(Flatten())
## Classification
# 全联接层
model.add(Dense(128, activation='relu'))
# Dropout 50% 的输入神经元
model.add(Dropout(0.5))
# 使用 softmax 激活函数做多分类,输出各数字的概率
model.add(Dense(n_classes, activation='softmax'))
ini
model.summary()
#%%
model.compile(loss='categorical_crossentropy', metrics=['accuracy'], optimizer='adam')
history = model.fit(X_train,
Y_train,
batch_size=128,
epochs=5,
verbose=2,
validation_data=(X_test, Y_test))