算法（keep learning）

基础算法

背模板加刷题

排序

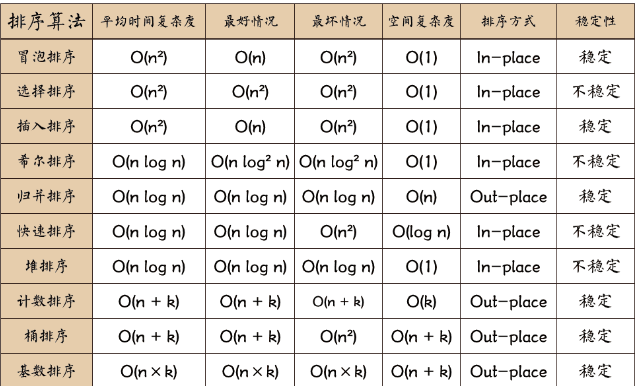
快排

主要思想：分治

• 第一步：确认一个分界点，比如起点，中间点（分界点），末点

• 第二步：调整区间，使得第一个区间的数都小于等于分界点，第二个区间都大于分界点

• 递归处理左右两端

  private static int[] quickSort(int[] arr, int left, int right) {
  // 递归终止条件，如果左边界大于等于右边界则认为递归结束
  if (left >= right) {
  return arr;
  }
  // 设定一个分界值，这里是（left + right）/ 2
  int p = arr[left + right >> 1];
  // 左右提前预留一个位置
  int i = left - 1;
  int j = right + 1;
  while (i < j) {
  // 等效于do while
  // 当数值小于分界值时持续遍历，直到找到第一个大于等于分界值的索引
  // 如果是逆序则调整两个while循环
  while (arr[++i] < p)
  ;
  while (arr[--j] > p)
  ;
  // 交换左右两侧不符合预期的数值
  if (i < j) {
  int temp = arr[i];
  arr[i] = arr[j];
  arr[j] = temp;
  }
  }
  // 由于分界值取的是left + right >> 1，因此递归取的是left，j j + 1，right
  quickSort(arr, left, j);
  quickSort(arr, j + 1, right);
  return arr;
  }

归并排序

归并排序本质上就是分治！

但是跟快排的分治方法不一样

• 以整个数组的中间点划分

• 递归排序两边

• 将两个有序的数组合并

  private static int[] mergeSort(int[] arr, int left, int right) {
  // 递归终止条件，如果左边界大于等于右边界则认为递归结束
  if (left >= right) {
  return arr;
  }
  // 设定一个分界值，这里是（left + right）/ 2
  int mid = left + right >> 1; // 位运算
  // 切割
  arr = mergeSort(arr, left, mid);
  arr = mergeSort(arr, mid + 1, right);
  // 归并，长度刚好是 left 到 right
  int[] temp = new int[right - left + 1];
  int i = left;
  int j = mid + 1;
  // 用来归并的索引
  int k = 0;
  while (i <= mid && j <= right) {
  // 如果是逆序则调整if条件
  if (arr[i] <= arr[j]) {
  temp[k++] = arr[i++];
  } else {
  temp[k++] = arr[j++];
  }
  }
  while (i <= mid) {
  temp[k++] = arr[i++];
  }
  while (j <= right) {
  temp[k++] = arr[j++];
  }
  // 根据归并后的数组重新赋值排序后的数组
  for (i = left, j = 0; i <= right; i++, j++) {
  arr[i] = temp[j];
  }
  return arr;
  }

二分

两种模板，分别是 LBS，和 RBS

// 检查x是否满足某种性质  
private static boolean check(int x) {  
   /* ... */  
}  

// 区间[left, right]被划分成[left, mid]和[mid + 1, right]时使用： 
// 或者称之为左二分查询，查找左侧第一个满足条件的数
private static int leftBinarySearch(int[] arr, int left, int right) {  
   while (left < right) {  
      int mid = arr[left + right >> 1];  
      if (check(mid)) {  
         right = mid;    // check()判断mid是否满足性质  
      } else {  
         left = mid + 1;  
      }  
   }  
   return left;  
}  

// 区间[left, right]被划分成[left, mid - 1]和[mid, right]时使用：  
// 或者称之为右二分查询，查找右侧最后一个满足条件的数
private static int rightBinarySearch(int[] arr, int left, int right) {  
   while (left < right) {  
      int mid = arr[left + right + 1 >> 1];  
      if (check(mid)) {  
         left = mid;    // check()判断mid是否满足性质  
      } else {  
         right = mid - 1;  // 有加必有减
      }  
   }  
   return left;  
}