动态规划入门：从记忆化搜索到动态规划

在开始对动态规划的讲解之前，我们需要先对记忆化搜索进行回顾：

什么是记忆化搜索？

在搜索过程中，当搜索树中存在大量重复的节点时，我们可以通过引入一个"备忘录"（通常是一个数组或哈希表）来优化计算。这个备忘录会记录第一次搜索到某个节点时的计算结果。当后续再次遇到相同的节点时，就可以直接从备忘录中获取之前存储的结果，避免了重复计算的开销。

例如，在计算斐波那契数列时，fib(5) = fib(4) + fib(3)，而fib(4)又需要计算fib(3)+fib(2)。如果不使用记忆化，fib(3)会被重复计算多次。使用记忆化后，每个fib(n)只需计算一次。

递推改递归 ：

在用记忆化搜索解决斐波那契数列问题时，如果我们观察备忘录的填写过程，会发现它是一个从左到右依次填充的过程。具体来说：

先计算并存储fib(0)和fib(1)的基础值
然后根据这两个值计算fib(2)
接着用fib(1)和fib(2)计算fib(3)
以此类推，每个新值都依赖于前面已计算好的值

这种自底向上的计算方式，实际上就是将递归过程改写成了循环形式的递推。这种改写不仅减少了函数调用的开销，还使得计算过程更加直观。

什么是动态规划？

动态规划(Dynamic Programming)是一种用于解决多阶段决策问题的算法思想。它将复杂问题分解为多个相互关联的子问题（称为状态），并通过保存子问题的解来避免重复计算，从而显著提高算法效率。

动态规划通常适用于具有以下特征的问题：

最优子结构：问题的最优解包含其子问题的最优解
重叠子问题：不同的决策序列会到达相同的子问题

从上述描述可以看出，动态规划结合了分治法的思想（将问题分解为子问题）和剪枝的思想（通过存储结果避免重复计算）。典型的应用场景包括：

最短路径问题（如Floyd算法）
背包问题
最长公共子序列
编辑距离计算

（在这篇文章中，笔者只讲解最基础的动态规划，典序应用场景的运用将留到后续更新中）

在递推形式的动态规划中，我们常用下面的专有名词来表述，因此，要学好并利用好动态规划，我们首先要弄清楚每一题中一下的概念：

状态表示：指 f 数组（备忘录）中，每一个格子所代表的含义。其中，这个数组也被称为dp数组，或者dp表。
状态转移方程：指 f 数组中，每一个格子是如何利用其他格子推导出来的。
初始化：在填表之前，根据题目中默认条件或问题的默认初始状态，将 f 数组中若干格子先填上值。

例题辅助理解：

光讲概念我相信很多小伙伴不能很好的理解或是看不懂，接下来，笔者将通过两个例题来帮助理解。

下楼梯：顽皮的小明发现，下楼梯时每步可以走 1 个台阶、2 个台阶或 3 个台阶。现在一共有 N 个台阶，你能帮小明算算有多少种方案吗？（洛谷P10250下楼梯）

在没有特殊限制的情况下，下台阶问题可以转化为上台阶问题来处理。具体来说，相当于小明每次可选择上1、2 或 3 级台阶。当我们要到达第 i 级台阶时，可能来自 i - 1、i - 2 或 i - 3 级台阶。基于这一思路，可以自然地推导出对应的状态转移方程。具体的算法流程如下所示：

算法原理：

状态表示：f[i] 表示走到第 i 级台阶有多少种方案
状态转移方程：f[i] = f[i - 1] + f[i - 2] + f[i - 3]
初始化：f[1] = 1 ...根据题意自行填写
填表顺序：从小到大依次填写
最终结果：f[n]

代码实现：

cpp 复制代码

int main()
{
	cin >> n;
	f[1] = 1, f[2] = 2, f[3] = 4;
	for (int i = 4; i <= n; i++)
		f[i] = f[i - 1] + f[i - 2] + f[i - 3];

	cout << f[n] << endl;
	return 0;
}

空间优化：通过采用滚动数组技术循环利用数组，可以有效降低空间复杂度。空间优化：通过采用滚动数组技术循环利用数组，可以有效降低空间复杂度。

cpp 复制代码

int main()
{
	cin >> n;
	f[1] = 1, f[2] = 2, f[3] = 4;
	for (int i = 4; i <= n; i++)
		f[i % 4] = f[(i - 1) % 4] + f[(i - 2) % 4] + f[(i - 3) % 4];

	cout << f[n % 4] << endl;
	return 0;
}

数字三角形：观察下面的数字金字塔。写一个程序来查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点（洛谷P1216数字三角形）。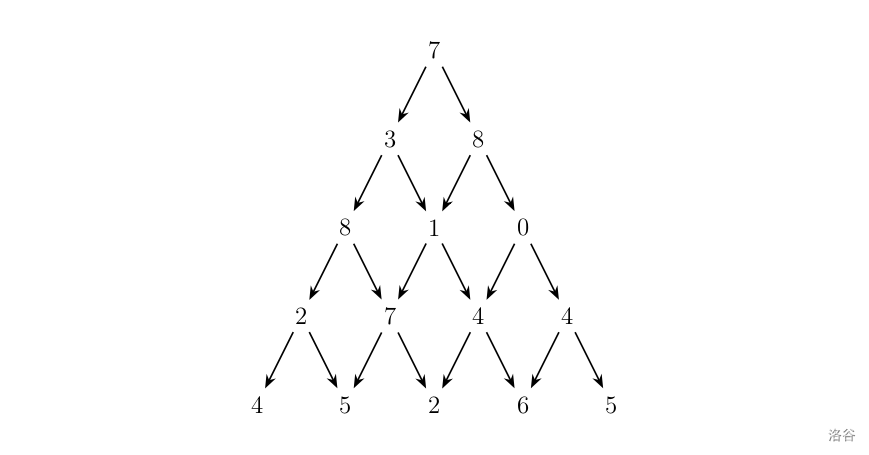

在题目中，要求我们找到一条最大路径，但在这个问题中，我们不能使用贪心算法（易证，这里不再赘述），此时我们就需要使用动态规划的方式解决，每一个位置 f[i][j] 都是由位置 f[i-1][j-1] 或 f[i-1][j] 移动到的，因此，我们只需要找到max(f[i - 1][j - 1], f[i - 1][j])再加上 a[i][j] 即可找到从起点到达 f[i][j] 位置的最大路径。最后，我们只需要遍历一下 f 数组的最下面一行即可找出最大路径。

算法原理：

状态表示：f[i][j]表示从[1，1]走到[i，j]位置时，所有方案下的最大权值
状态转移方程： f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j]
初始化：将所有格子全部初始化为负无穷
填表顺序：仅需保证从上到下即可
最终结果：最后一行的最大值

代码实现：

cpp 复制代码

int main()
{
	cin >> n;
	memset(f, -0x3f, sizeof f);
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= i; j++)
			cin >> a[i][j];

	f[1][1] = a[1][1];

	for (int i = 2; i <= n; i++)
		for (int j = 1; j <= i; j++)
			f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j];

	int max = 0;
	for (int i = 1; i <= n; i++)
		if (f[n][i] > max)max = f[n][i];

	cout << max << endl;
	return 0;
}

空间优化：可以将 f 数组从二维降为一维。由于每次更新时都是从左到右顺序处理，且使用过的旧值不会被重复利用，因此可以不断覆盖原数组，仅保留一维数组来记录最终结果。可以将 f 数组从二维降为一维。由于每次更新时都是从左到右顺序处理，且使用过的旧值不会被重复利用，因此可以不断覆盖原数组，仅保留一维数组来记录最终结果。

cpp 复制代码

int main()
{
	cin >> n;
	memset(f, -0x3f, sizeof f);
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= i; j++)
			cin >> a[i][j];

	f[1] = a[1][1];

	for (int i = 2; i <= n; i++)
		for (int j = 1; j <= i; j++)
			f[j] = max(f[j - 1], f[j]) + a[i][j];

	int max = 0;
	for (int i = 1; i <= n; i++)
		if (f[i] > max)max = f[i];

	cout << max << endl;
	return 0;
}

谢谢阅读！更新不易，点个赞再走吧