【数据结构08】队列实现及练习

Doro再努力2026-01-12 18:14


🎬 Doro在努力 ：个人主页
🔥 个人专栏 : 《MySQL数据库基础语法》《数据结构》

⛺️严于律己，宽以待人

文章目录

一、队列的概念与结构

概念：只允许在一段进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出的特性。

  • 入队列：进行插入数据的一端称为队尾
  • 出队列：进行删除操作的一端称为对头
    ![[Pasted image 20251224001253.png]]
    队列也有数组和链表两种实现方式，使用链表的结构更优一些，因为如果使用数组的结构，出队列在数组的头上出数据，时间复杂度为O(N)，虽然链表在队尾的插入数据时间复杂度为O(N)，但是我们可以单独再定义一个指向尾节点的指针ptail就可以有效解决尾部插入数据的问题，而数组要头插是必须挪动数据的，因此使用链表来实现队列效率会比使用数组高。

二、队列的实现

2.1队列的定义

我们在队列中插入删除数据都是在队头或者队尾，对于链表中间的节点我们是不关注的，因此在我们的队列结构体中，只需要创建指向队头节点和队尾节点的指针就行，同时节点、节点，我们队列是在链表的基础上创建的，因此指针类型是链表的节点类型，具体实现如下：

c 复制代码 
//Queue.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef struct QueueNode QueueNode;
typedef int QDataTpye;
struct QueueNode//链表节点
{
	QDataTpye data;
	struct QueueNode* next;
};

//定义队列
struct Queue
{
	QueueNode* phead;//头节点
	QueueNode* ptail;//尾节点
};

2.2初始化函数

初始化函数传入一级指针，这是因为我们定义的是Queue q,需要通过形参改变实参的值，然后初始化将队头、队尾两个指针都置为NULL，具体代码如下：

c 复制代码 
//初始化函数
void QueueIint(Queue* pq)
{
	assert(pq);//不能传入空指针
	pq->phead = pq->ptail = NULL;
}

2.3入队函数

队列的插入是在队尾插入，malloc创建一个节点，然后在队尾进行插入，最后让队尾指针向后挪动一个位置。示意图和具体代码如下：

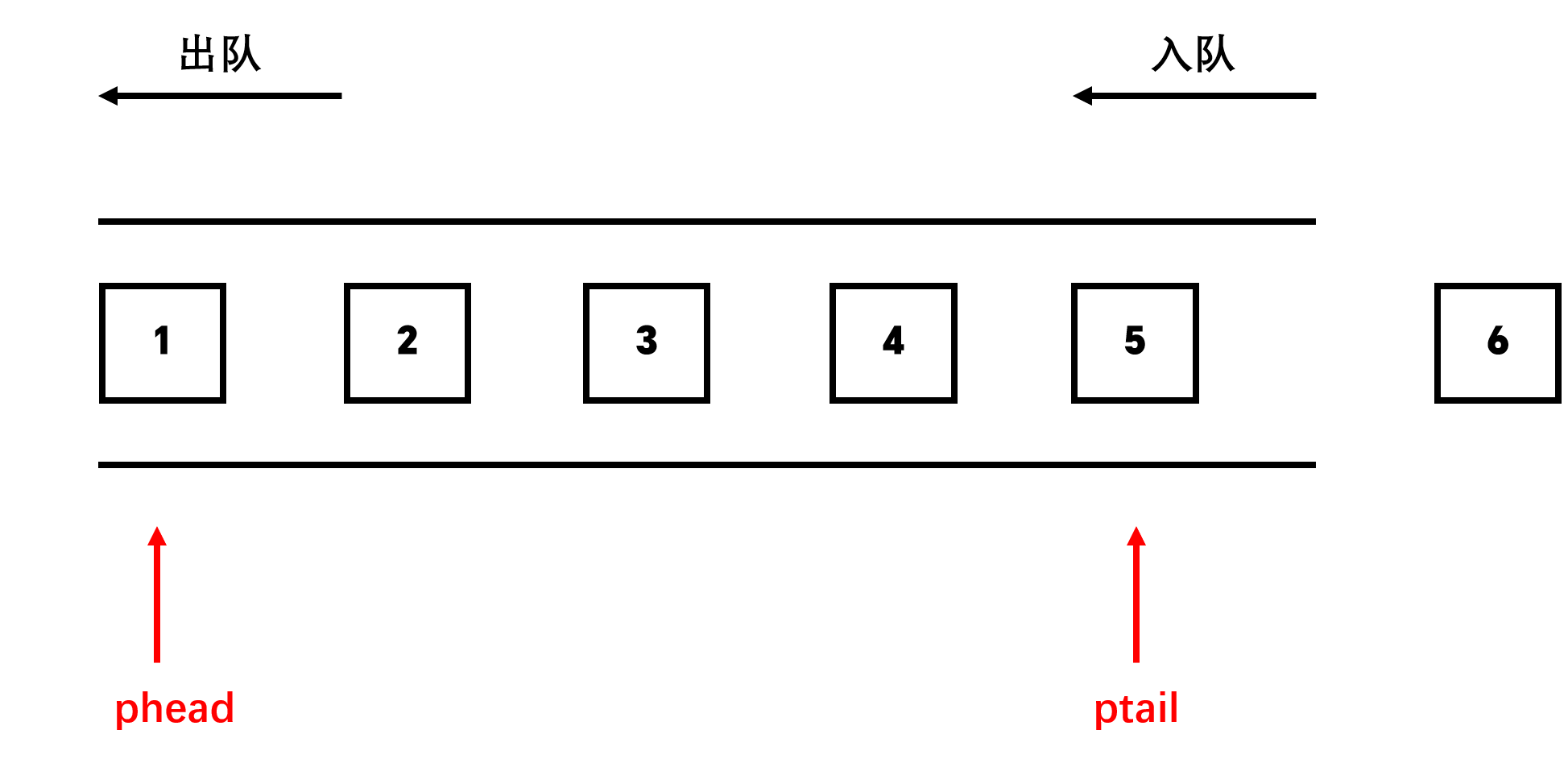
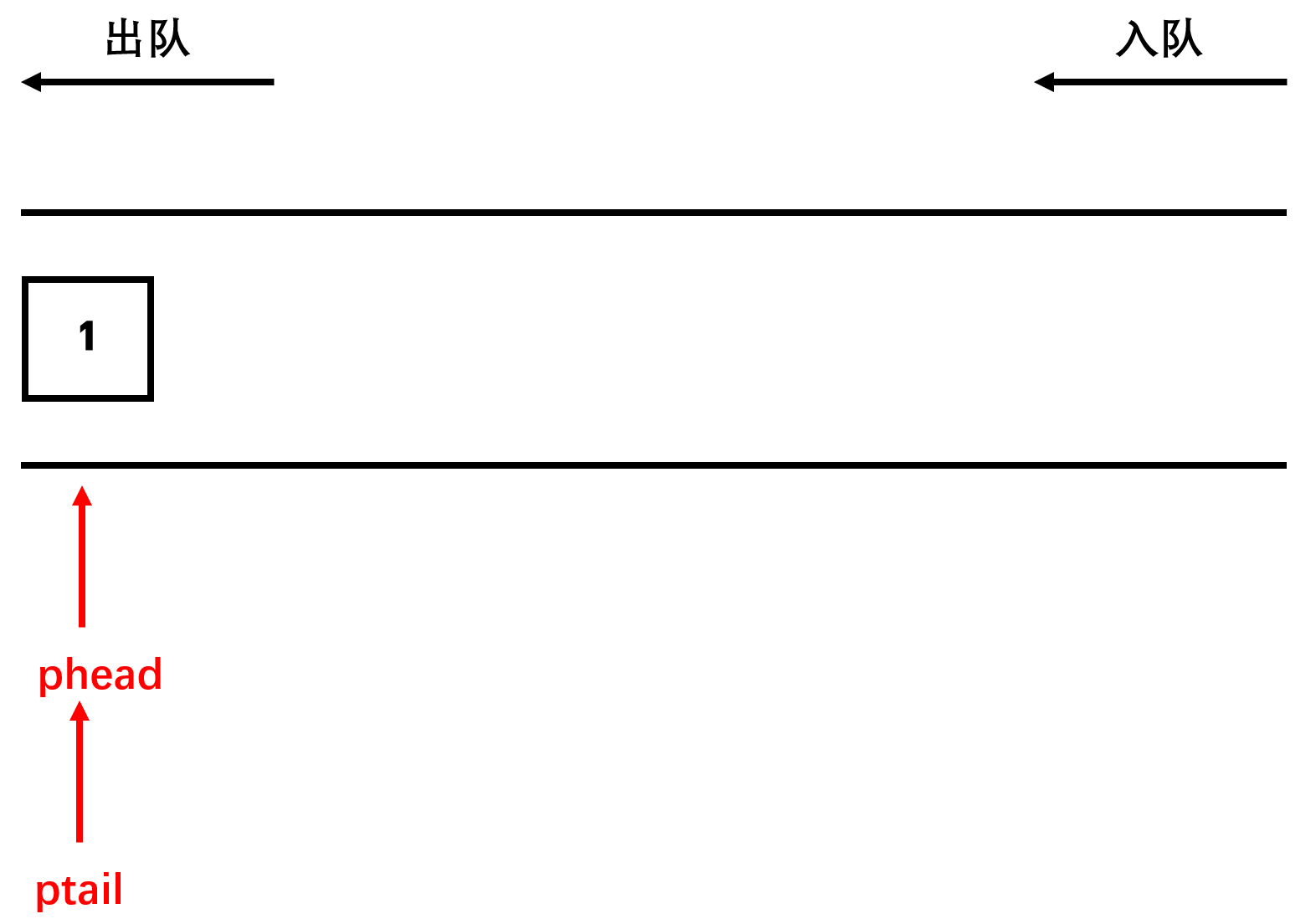
c 复制代码 
//入队函数
void QueuePush(Queue* pq,QDataType x)
{
	assert(pq);
	//创建新节点
	QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
	if (newnode == NULL)
	{
		perror("malloc fail!\n");
		exit(-1);
	}
	newnode->data = x;
	newnode->next = NULL;
	//原队头为空
	if (pq->phead == NULL)//还未插入元素
	{
		pq->phead = pq->ptail = newnode;//队头、队尾指针都指向新节点
	}
	//原队头不为空
	pq->ptail->next = newnode;//队尾节点的下一个节点指向新节点
	pq->ptail = pq->ptail->next;//队尾指向向后移动一位
}

2.4出队函数

从队列中出数据是在队头出数据，出数据需要将malloc的空间释放，对于的指针置为空，然后队头指针向后挪动一位。示意图如下：

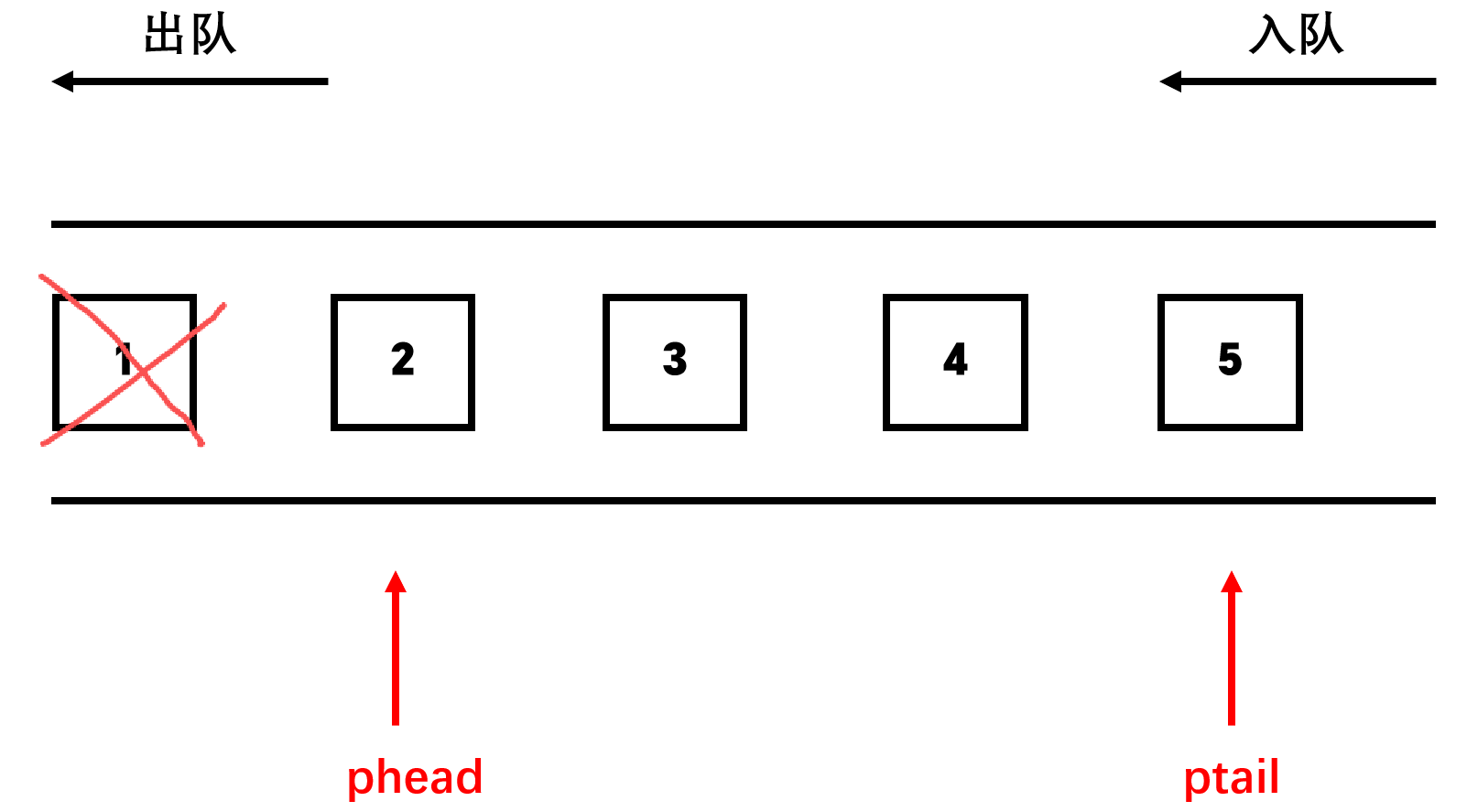
同时需要注意的是，在出队列之前需要判断队列中是否有节点，只有有节点的时候才需要出队，因此同步实现判空函数，具体代码如下：

c 复制代码 
//判空函数
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->phead == NULL;
}

//出队函数
void QueuePop(Queue* pq)
{
	assert(!QueueEmpty(pq));
	//队列中只有一个节点
	if (pq->phead == pq->ptail)
	{
		free(pq->phead);
		pq->phead = pq->ptail = NULL;
	}
	else
	{
		QueueNode* del = pq->phead;
		pq->phead = pq->phead->next;
		free(del);
		del = NULL;
	}
}

2.5取队头队尾函数

取队头、队尾的数值直接访问对于指针的数据域即可获得队头、队尾的数值，具体代码如下：

c 复制代码 
//取队头函数
QDataType QueueFront(Queue* pq)
{
	assert(pq);
	return pq->phead->data;//直接访问队头指针的数值域
}

//取队尾函数
QDataType QueueBack(Queue* pq)
{
	assert(pq);
	return pq->ptail->data;//直接访问队尾指针的数值域
}

2.6取有效元素个数函数

取队列中有效元素个数，只需要用一个工作指针指向头节点，然后依次往后遍历，只要不为NULL，则计数变量size就++，具体代码如下：

c 复制代码 
//取有效元素个数函数
int QueueSize(Queue* pq)
{
	assert(pq);
	QueueNode* pcur = pq->phead;
	int size = 0;
	while (pcur)
	{
		size++;//只要pcur不为空
		pcur = pcur->next;//工作指针向后挪动一位
	}
	return size;
}

队列的插入、删除、取数据的时间复杂度都是O(1)，只有这里的取有效元素个数的时间复杂的为O(N)，想让取有效元素个数的时间复杂度降为O(1)，也是可以的，只需要在定义队列时，加一个成员变量size，每次插入、删除节点时对size成员进行修改，最后就可以非常方便的拿到有效元素个数。

2.7销毁函数

销毁队列其实就是销毁队列中的每一个节点，然后将队头和队尾指针置空，具体代码如下：

c 复制代码 
//销毁函数
void QueueDesTroy(Queue* pq)
{
	assert(pq);
	QueueNode* pcur = pq->phead;//保留队头指针的指向
	while (pcur)
	{
		pq->phead = pq->phead->next;//先让队头指针后移一位
		free(pcur);//释放原队头节点
		pcur = pq->phead;//找到新队头节点
	}
	pq->phead = pq->ptail = pcur = NULL;
}

2.8全部代码

c 复制代码 
//test.c
#include"Queue.h"
void test01()
{
	Queue q;
	QueueIint(&q);
	QueuePush(&q, 1);
	QueuePush(&q, 2);
	QueuePush(&q, 3);
	QueuePush(&q, 4);
	QueuePush(&q, 5);
	QueuePop(&q);
	QueuePop(&q);
	printf("%d\n", QueueFront(&q));
	printf("%d\n", QueueBack(&q));
	printf("%d\n", QueueSize(&q));
	QueueDesTroy(&q);
}
int main()
{
	test01();
	return 1;
}
c 复制代码 
//Queue.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef struct QueueNode QueueNode;
typedef int QDataType;
struct QueueNode//链表节点
{
	QDataType data;
	struct QueueNode* next;
};
//定义队列
struct Queue
{
	QueueNode* phead;//头节点
	QueueNode* ptail;//尾节点
};
//初始化函数
void QueueIint(Queue* pq);
//销毁函数
void QueueDesTroy(Queue* pq);
//入队函数
void QueuePush(Queue* pq,QDataType x);
//出队函数
void QueuePop(Queue* pq);
//判空函数
bool QueueEmpty(Queue* pq);
//取队头函数
QDataType QueueFront(Queue* pq);
//取队尾函数
QDataType QueueBack(Queue* pq);
//取有效元素个数函数
int QueueSize(Queue* pq);
c 复制代码 
//Queue.cpp
#define _CRT_SECURE_NO_WARNINGS 1
#include"Queue.h"
//初始化函数
void QueueIint(Queue* pq)
{
	assert(pq);//不能传入空指针
	pq->phead = pq->ptail = NULL;
}
//入队函数
void QueuePush(Queue* pq,QDataType x)
{
	assert(pq);
	//创建新节点
	QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
	if (newnode == NULL)
	{
		perror("malloc fail!\n");
		exit(-1);
	}
	newnode->data = x;
	newnode->next = NULL;
	//原队头为空
	if (pq->phead == NULL)//还未插入元素
	{
		pq->phead = pq->ptail = newnode;//队头、队尾指针都指向新节点
	}
	//原队头不为空
	pq->ptail->next = newnode;//队尾节点的下一个节点指向新节点
	pq->ptail = pq->ptail->next;//队尾指向向后移动一位
}
//判空函数
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->phead == NULL;
}
//出队函数
void QueuePop(Queue* pq)
{
	assert(!QueueEmpty(pq));
	//队列中只有一个节点
	if (pq->phead == pq->ptail)
	{
		free(pq->phead);
		pq->phead = pq->ptail = NULL;
	}
	else
	{
		QueueNode* del = pq->phead;
		pq->phead = pq->phead->next;
		free(del);
		del = NULL;
	}
}
//取队头函数
QDataType QueueFront(Queue* pq)
{
	assert(!QueueEmpty(pq));
	return pq->phead->data;//直接访问队头指针的数值域
}
//取队尾函数
QDataType QueueBack(Queue* pq)
{
	assert(!QueueEmpty(pq));
	return pq->ptail->data;//直接访问队尾指针的数值域
}
//取有效元素个数函数
int QueueSize(Queue* pq)
{
	assert(pq);
	QueueNode* pcur = pq->phead;
	int size = 0;
	while (pcur)
	{
		size++;//只要pcur不为空
		pcur = pcur->next;//工作指针向后挪动一位
	}
	return size;
}
//销毁函数
void QueueDesTroy(Queue* pq)
{
	assert(pq);
	if (QueueEmpty(pq)) return;  // 如果队列已经为空，直接返回
	QueueNode* pcur = pq->phead;
	while (pcur)
	{
		QueueNode* next = pcur->next;  // 保存下一个节点
		free(pcur);                    // 释放当前节点
		pcur = next;                   // 移动到下一个节点
	}
	pq->phead = pq->ptail = NULL;      // 重置队列头尾指针
}

三、队列的算法题

3.1 用队列实现栈

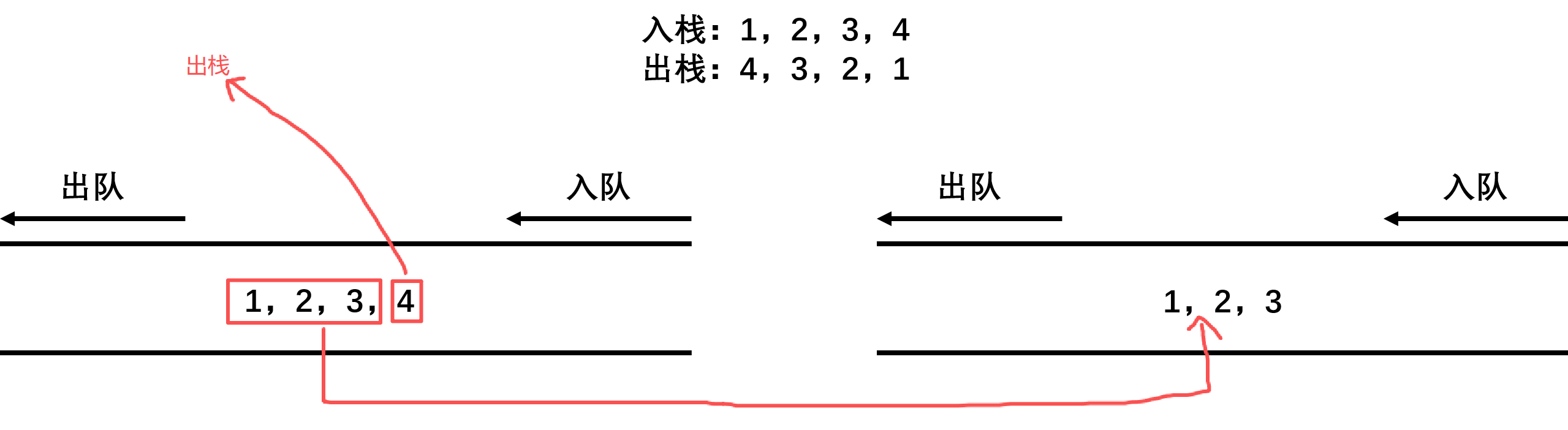
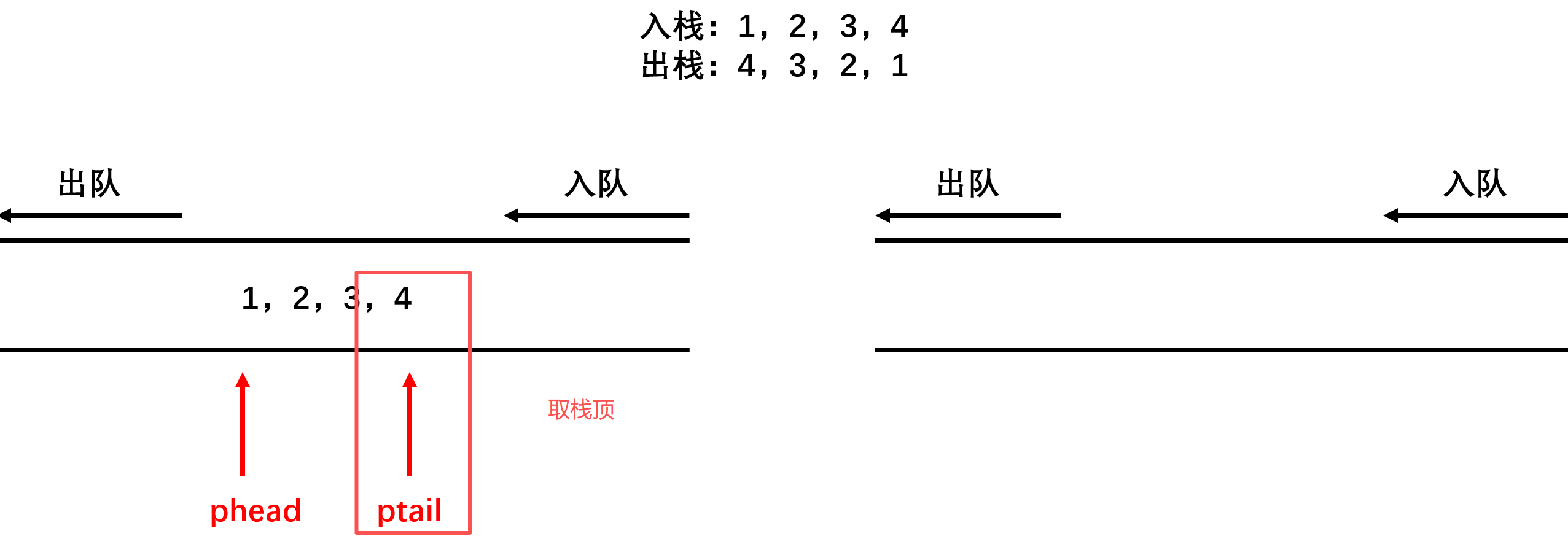
用两个队列实现栈，需要两个队列分工合作，入栈操作就是向不为空的队列中插入数据，出栈操作就是将前size-1个数据依次入队到为空的队列，最后将原队列剩下的数据出队就是要出栈的结果。取栈顶操作不出数据，找不为空的队列，返回队尾数据。

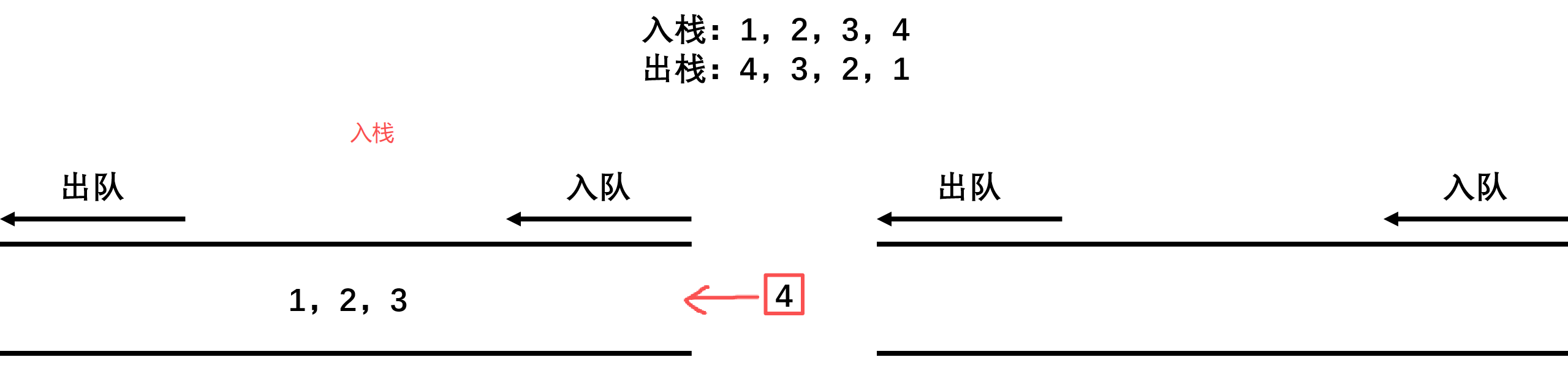
c 复制代码 
typedef int QDataType;

typedef struct QueueNode

{

    QDataType data;

    struct QueueNode* next;

}QueueNode;

  

typedef struct Queue

{

    QueueNode* phead;

    QueueNode* ptail;

}Queue;

  

//队列的初始化

void QueueInit(Queue* pq)

{

    assert(pq);

    pq->phead = pq->ptail = NULL;

}

  

//入队

void QueuePush(Queue* pq, QDataType x)

{

    assert(pq);

    //申请新节点

    QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));

    if (newnode == NULL)

    {

        perror("malloc fail!");

        exit(1);

    }

    newnode->data = x;

    newnode->next = NULL;

  

    //如果队列为空

    if (pq->phead == NULL)

    {

        pq->phead = pq->ptail = newnode;

    }

    else

    {

        pq->ptail->next = newnode;

        pq->ptail = pq->ptail->next;

    }

}

  

//队列判空

bool QueueEmpty(Queue* pq)

{

    assert(pq);

    return pq->phead == NULL;

}

  

//出队

void QueuePop(Queue* pq)

{

    assert(!QueueEmpty(pq));

    //如果队伍中只有一个节点

    if (pq->phead == pq->ptail)

    {

        free(pq->phead);

        pq->phead = pq->ptail = NULL;

    }

    else

    {

        QueueNode* next = pq->phead->next;

        free(pq->phead);

        pq->phead = next;

    }

}

  

//取队首数据

QDataType QueueHead(Queue* pq)

{

    assert(!QueueEmpty(pq));

    return pq->phead->data;

}

  

//取队尾数据

QDataType QueueTail(Queue* pq)

{

    assert(!QueueEmpty(pq));

    return pq->ptail->data;

}

  

//队列有效数据个数

int QueueSize(Queue* pq)

{

    QueueNode* pcur = pq->phead;

    int size = 0;

    while (pcur)

    {

        ++size;

        pcur = pcur->next;

    }

    return size;

}

  

//队列的销毁

void QueueDestroy(Queue* pq)

{

    assert(pq);

    QueueNode* pcur = pq->phead;

    while (pcur)

    {

        QueueNode* next = pcur->next;

        free(pcur);

        pcur = next;

    }

    pq->phead = pq->ptail = NULL;

}

  

//----------------------以上是队列结构的定义和常用方法----------------------------

typedef struct {

    Queue q1;

    Queue q2;

} MyStack;

  

//创建一个栈

MyStack* myStackCreate() {

    MyStack* pter = (MyStack*)malloc(sizeof(MyStack));

    QueueInit(&pter->q1);

    QueueInit(&pter->q2);

    return pter;

}

  

void myStackPush(MyStack* obj, int x) {

    //如果q1为空，往q1里插入数据，反之则是往q2里插入数据

    if(!QueueEmpty(&obj->q1))

    {

        //q1

        QueuePush(&obj->q1,x);

    }

    else{

        //q2

        QueuePush(&obj->q2,x);

    }

}

  

int myStackPop(MyStack* obj) {

    //先假设一个为空

    Queue* emp = &obj->q1;

    Queue* nonemp = &obj->q2;

    if(QueueEmpty(&obj->q2))

    {

        emp = &obj->q2;

        nonemp = &obj->q1;

    }

    //将非空队列中前size-1个数据挪到另一个队列中

    while(QueueSize(nonemp) > 1)

    {

        //取队头数据，插入空队列中

        QueuePush(emp, QueueHead(nonemp));

        //出数据

        QueuePop(nonemp);

    }

    //将非空队列中最后一个数据出队列,注意返回类型为int出之前先存一下

    int top = QueueHead(nonemp);

    QueuePop(nonemp);

    return top;

}

  

int myStackTop(MyStack* obj) {

    if(!QueueEmpty(&obj->q1))

    {

        //取q1的队尾数据,并返回

        return QueueTail(&obj->q1);

    }

    else{

        //取q2的队尾数据,并返回

        return QueueTail(&obj->q2);

    }

}

  

bool myStackEmpty(MyStack* obj) {

    //全为空即为空

    return (QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2));

}

  

void myStackFree(MyStack* obj) {

    QueueDestroy(&obj->q1);

    QueueDestroy(&obj->q2);

    free(obj);

    obj = NULL;

}

  

/**

 * Your MyStack struct will be instantiated and called as such:

 * MyStack* obj = myStackCreate();

 * myStackPush(obj, x);

 * int param_2 = myStackPop(obj);

 * int param_3 = myStackTop(obj);

 * bool param_4 = myStackEmpty(obj);

 * myStackFree(obj);

*/

3.2用栈实现队列

上一道算法题我们用队列实现了栈，现在我们继续尝试用栈实现队列。用两个栈结构实现队列，需要将一个栈设置为PushST入队栈，一个栈设置为PopST出队栈。

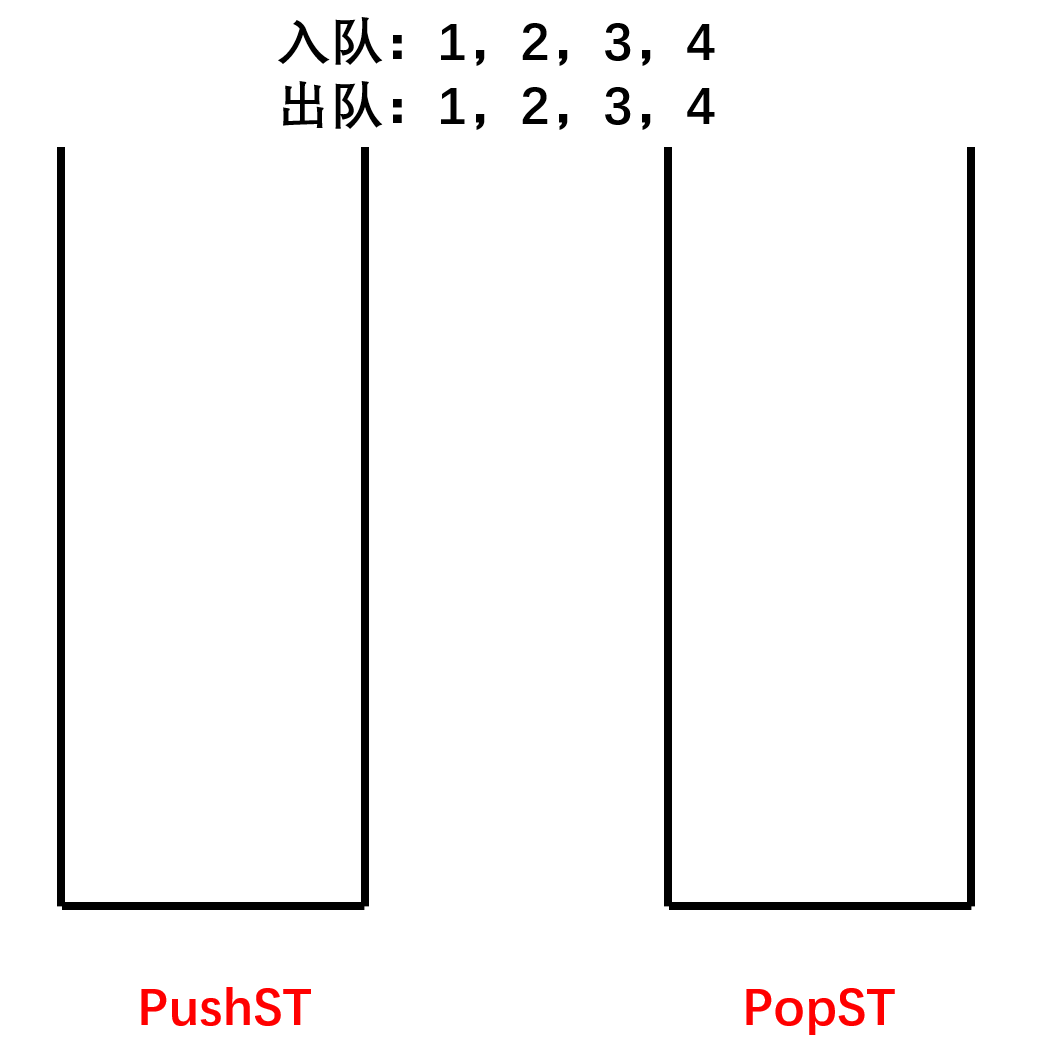
入队列时，将需要入队的数据插入到PushST栈中。出队列时，将PushST中的所有数据出栈，再入栈到PopST中，接着将PopST栈中的数据依次出栈。

需要注意的是，出栈时要判断PopST栈是否为空，如果非空，则要先将PopST中的数据全部出栈，再将PushST中的数据导入到PopST中依次出栈。

取队头操作和出队列一样，但是不出数据，PopST不为空直接取队头，否组将PushST中的数据先导到PopST中，再取队头。

c 复制代码 
  

typedef int STDataType;

typedef struct Stack ST;

  

struct Stack

{

    STDataType* arr;//指向栈的指针

    int top;//指向栈顶的位置（在数组中也为栈的有效元素个数)

    int capacity;//栈的空间大小

};

  

//初始化函数

void STIint(ST* ps)

{

    assert(ps);

    ps->arr = NULL;

    ps->top = ps->capacity = 0;

}

  

//销毁函数

void STDesTroy(ST* ps)

{

    if(ps->arr)

        free(ps->arr);//释放数组空间

    ps->arr = NULL;

    ps->top = ps->capacity = 0;

}

  

//入栈------栈顶

void STPush(ST* ps,STDataType x)

{

    assert(ps);

    if (ps->top == ps->capacity)//判断是否存满

    {

        int newcapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;//如果为空，则先初始化为4,否则进行二倍扩容

  

        STDataType* tmp = ps->arr;

        tmp = (STDataType*)realloc(tmp, newcapacity * sizeof(STDataType));

        if (tmp == NULL)

        {

            perror("realloc fail!\n");

            exit(1);

        }

        ps->arr = tmp;//将新开辟的空间赋值给数组指针

        ps->capacity = newcapacity;//将新空间的大小赋值给capacity

    }

    ps->arr[ps->top] = x;//插入数据

    ps->top++;//栈顶+1

}

  

//判空函数

bool STEmpty(ST* ps)

{

    assert(ps);

    return ps->top == 0;//返回栈顶是否为0的判断结果

}

  

//出栈

void STPop(ST* ps)

{

    assert(!STEmpty(ps));//如果ps->为空，则STEmpty(ps)结果为false,!STEmpty结果为假，断言报错

    ps->top--;

}

  

//取栈顶元素

STDataType STTop(ST* ps)

{

    assert(!STEmpty(ps));

    return ps->arr[ps->top - 1];

}

  

//获取栈中有效元素个数

int STSize(ST* ps)

{

    assert(ps);

    return ps->top;

}

//------------以上是栈结构的常见定义和方法------------------------

  

typedef struct {

    ST PushST;

    ST PopST;

} MyQueue;

  
  

MyQueue* myQueueCreate() {

    MyQueue* pq = (MyQueue*)malloc(sizeof(MyQueue));

    STIint(&pq->PushST);

    STIint(&pq->PopST);

    return pq;

}

  

//入队列

void myQueuePush(MyQueue* obj, int x) {

    //直接向PushST栈中入数据

    STPush(&obj->PushST,x);

}

  

//出数据

int myQueuePop(MyQueue* obj) {

    //PopST为空，将PushST的数据全部导入到PopST中

    if(STEmpty(&obj->PopST))

    {

        while(!STEmpty(&obj->PushST))

        {

            //取栈顶，入PopST栈，出栈

            STPush(&obj->PopST,STTop(&obj->PushST));

            STPop(&obj->PushST);

        }

    }

    //PopST不为空直接出

    int top = STTop(&obj->PopST);

    STPop(&obj->PopST);

    return top;

}

  

//取队头

int myQueuePeek(MyQueue* obj) {

        if(STEmpty(&obj->PopST))

    {

        while(!STEmpty(&obj->PushST))

        {

            STPush(&obj->PopST,STTop(&obj->PushST));

            STPop(&obj->PushST);

        }

    }

    int top = STTop(&obj->PopST);

    //不用出栈

    return top;

}

  

bool myQueueEmpty(MyQueue* obj) {

    return STEmpty(&obj->PushST)&&STEmpty(&obj->PopST);

}

  

void myQueueFree(MyQueue* obj) {

    STDesTroy(&obj->PushST);

    STDesTroy(&obj->PopST);

    free(obj);

    obj = NULL;

}

  

/**

 * Your MyQueue struct will be instantiated and called as such:

 * MyQueue* obj = myQueueCreate();

 * myQueuePush(obj, x);

 * int param_2 = myQueuePop(obj);

 * int param_3 = myQueuePeek(obj);

 * bool param_4 = myQueueEmpty(obj);

 * myQueueFree(obj);

*/

这样，我们就完成了数据结构队列的相关学习，接下来我们将进入二叉树内容的相关学习，敬请期待！

相关推荐
清铎5 小时前
leetcode_day12_滑动窗口_《绝境求生》
python·算法·leetcode·动态规划
linweidong5 小时前
嵌入式电机：如何在低速和高负载状态下保持FOC（Field-Oriented Control）算法的电流控制稳定？
stm32·单片机·算法
net3m335 小时前
单片机屏幕多级菜单系统之当前屏幕号+屏幕菜单当前深度 机制
c语言·c++·算法
mmz12075 小时前
二分查找（c++）
开发语言·c++·算法
Insight5 小时前
拒绝手动 Copy！一文吃透 PyTorch/NumPy 中的广播机制 (Broadcasting)
算法
CoovallyAIHub6 小时前
工业视觉检测：多模态大模型的诱惑
深度学习·算法·计算机视觉
Jayden_Ruan6 小时前
C++分解质因数
数据结构·c++·算法
bubiyoushang8886 小时前
MATLAB实现雷达恒虚警检测
数据结构·算法·matlab
wu_asia6 小时前
编程技巧：如何高效输出特定倍数数列
c语言·数据结构·算法
热门推荐
01GitHub 镜像站点02Labelme从安装到标注：零基础完整指南03安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）04Linux下V2Ray安装配置指南05Claude Code 2.1.2 升级报错？别折腾了，一行命令搞定062025-04-03 Latex学习1——本地配置Latex + VScode环境07jdk21下载、安装（Windows、Linux、macOS）08【踩坑笔记】50系显卡适配的 PyTorch 安装09Overleaf编译超时，超出免费计划编译时限（已解决）10KGG转MP3工具|非KGM文件|解密音频