一、基础认知
1.1 什么是决策树?
-
本质:模拟人类决策过程的树形结构
-
组成:
-
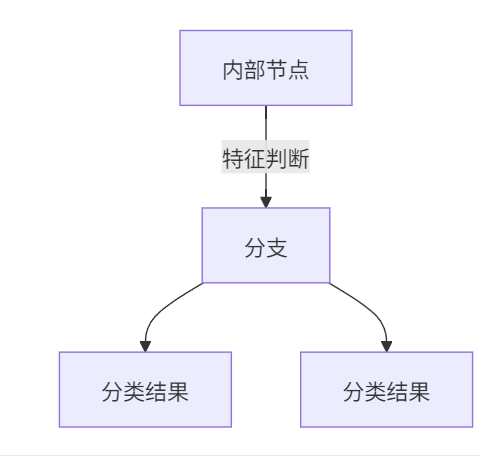
-
实例 :相亲决策流程
年龄 > 30? → 是 → 拒绝 ↓ 否 收入 > 50万? → 是 → 接受 ↓ 否 公务员? → 是 → 接受 ↓ 否 → 拒绝
1.2 核心概念对比
| 概念 | ID3决策树 | C4.5决策树 | CART决策树 |
|---|---|---|---|
| 分裂依据 | 信息增益最大 | 信息增益率最大 | 基尼指数最小 |
| 树结构 | 多叉树 | 多叉树 | 二叉树 |
| 支持任务 | 分类 | 分类 | 分类+回归 |
| 缺陷 | 偏向多值特征 | 计算复杂度高 | 只能二叉树分裂 |
二、核心数学原理(附图解)
2.1 信息熵:混乱度度量
-
公式 :
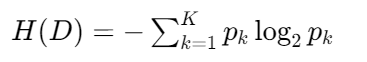
-
实例 :
数据集A:[A,B,C,D] → 熵 = -4×(1/4)×log₂(1/4) = 2.0 数据集B:[A,A,A,B] → 熵 = -[(3/4)log₂(3/4)+(1/4)log₂(1/4)] ≈ 0.81结论:数据越纯净,熵值越小
2.2 信息增益(ID3核心)
-
计算流程 :
1. 计算父节点熵值 H(D) 2. 按特征分裂后计算子节点加权熵 ∑(子样本数/总样本数)×H(子) 3. 信息增益 = H(D) - 子节点加权熵 -
实例演算 (7人拖欠贷款数据集):
特征\结果 拖欠(Yes) 不拖欠(No) 计算 有房 0 3 熵=0 无房 3 4 熵≈0.985 信息增益 = 0.985 - (3/10)×0 + (7/10)×0.985 ≈ 0.69
2.3 信息增益率(C4.5核心)
-
公式 :
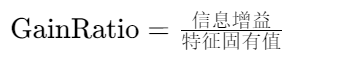
-
修正原理 :
特征"邮编"有1000个取值 → 固有值很大 → 增益率变小 特征"性别"有2个取值 → 固有值小 → 增益率保留
2.4 基尼指数(CART核心)
-
公式 :
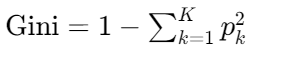
-
物理意义:随机抽两个样本,类别不一致的概率
-
实例 :
数据集[3个A,7个B]: Gini = 1 - [(3/10)² + (7/10)²] = 0.42
三、实战案例详解
3.1 泰坦尼克生存预测(分类树)
python
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
# 数据预处理
titanic = pd.read_csv('titanic.csv')
titanic['Age'].fillna(titanic['Age'].mean(), inplace=True) # 年龄缺失值填充
X = pd.get_dummies(titanic[['Pclass', 'Age', 'Sex']]) # 独热编码
y = titanic['Survived']
# 模型训练与评估
model = DecisionTreeClassifier(criterion='gini', max_depth=3)
model.fit(X_train, y_train)
print(f"准确率: {model.score(X_test, y_test):.2%}")
# 决策树可视化
from sklearn.tree import plot_tree
plot_tree(model, feature_names=X.columns, class_names=['Died','Survived'])关键输出:
precision recall f1-score support
Died 0.83 0.91 0.87 105
Survived 0.82 0.68 0.74 69
accuracy 0.83 1743.2 房价预测(回归树)
python
from sklearn.tree import DecisionTreeRegressor
# 生成波形数据
X = np.sort(5 * np.random.rand(80, 1), axis=0)
y = np.sin(X).ravel() + np.random.normal(0, 0.1, X.shape[0])
# 不同深度树对比
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=5)
regr_1.fit(X, y)
regr_2.fit(X, y)
# 可视化预测曲线
plt.plot(X_test, regr_1.predict(X_test), label="深度=2")
plt.plot(X_test, regr_2.predict(X_test), label="深度=5")结论:树深度越大,拟合能力越强(过拟合风险越高)
四、剪枝技术解析
4.1 为什么要剪枝?
- 过拟合现象:训练准确率99% → 测试准确率70%
- 根本原因:树过于复杂,学习了噪声数据
4.2 剪枝方法对比
| 类型 | 操作时机 | 优点 | 缺点 |
|---|---|---|---|
| 预剪枝 | 树生成过程中 | 训练快,减少计算资源 | 可能欠拟合(早停问题) |
| 后剪枝 | 生成完整树后 | 保留更多有效分支 | 计算开销大 |
4.3 剪枝效果演示
python
# 未剪枝 vs 预剪枝对比
full_tree = DecisionTreeClassifier() # 无限制
pruned_tree = DecisionTreeClassifier(max_depth=3, min_samples_leaf=5)
full_tree.fit(X_train, y_train)
pruned_tree.fit(X_train, y_train)
print(f"未剪枝测试集准确率: {full_tree.score(X_test, y_test):.2%}")
print(f"预剪枝测试集准确率: {pruned_tree.score(X_test, y_test):.2%}")典型输出:
未剪枝测试集准确率:76.34%
预剪枝测试集准确率:82.15% # 剪枝后泛化能力提升五、高频面试题解析
-
信息增益 vs 信息增益率
信息增益偏向多值特征(如"ID"字段),增益率通过除以特征固有值修正此问题
-
CART为何用基尼指数?
基尼指数计算只需加减乘(熵需要log运算),在大数据场景效率更高
-
如何处理连续特征?
步骤: 1. 排序特征值:[10, 20, 30, 40] 2. 计算候选切分点:(10+20)/2=15, (20+30)/2=25... 3. 选择最优切分点(基尼指数最小) -
决策树优缺点
优点 :可解释性强、无需特征缩放、支持混合数据类型
缺点:容易过拟合、对样本敏感、忽略特征间相关性
六、学习资源推荐
- 实践平台:Kaggle Titanic竞赛(决策树基线模型)
- 可视化工具 :
- Decision Tree Visualizer
- Graphviz + Scikit-learn联合可视化
- 进阶方向 :
- 集成学习:随机森林、GBDT
- 特征重要性分析:
model.feature_importances_