MixFormer: A Mixed CNN–Transformer Backbone

MixFormer: A Mixed CNN--Transformer Backbone

摘要

​ 尽管基于自注意力机制的Transformer模型近年来通过建模长程语义依赖关系推动了医学影像分析的发展，但其在捕捉局部空间细节方面的能力仍逊于卷积神经网络（CNN）。本研究提出了一种新型分割网络（SEG），其核心是基于CNN-Transformer混合架构（MixFormer）的特征提取主干网络，旨在提升医学图像分割性能。MixFormer在网络下采样过程中有机融合了Transformer的全局信息建模能力和CNN的局部特征提取优势。为全面捕捉跨尺度特征，我们设计了多尺度空间感知融合（MSAF）模块，有效实现了粗细粒度特征表征的交互。此外，我们提出混合多分支空洞注意力（MMDA）模块来弥合编码与解码阶段的语义鸿沟，同时强化关键区域的关注。最后采用基于CNN的上采样方法重建底层特征，显著提升了分割精度。

​ 在主流医学影像数据集上的实验验证表明MixFormer具有卓越性能：在Synapse数据集上取得82.64%的平均Dice相似系数（DSC）和12.67mm的平均豪斯多夫距离（HD）；在ACDC心脏数据集上DSC达91.01%；在ISIC2018皮肤影像数据集上获得0.841的平均交并比（mIoU）、0.958准确率、0.910精确率、0.934召回率及0.913 F1分数；在Kvasir-SEG数据集上实现0.9247平均Dice、0.8615 mIoU、0.9181精确率和0.9463召回率；在CVC-ClinicDB数据集上达到0.9441平均Dice、0.8922 mIoU、0.9437精确率和0.9458召回率。这些结果充分证明，相较于主流CNN分割网络及其他基于Transformer的结构，MixFormer具有更优异的分割性能。

INTRODUCTION

​ 医学图像分割（SEG）是医学图像处理中不可或缺的关键环节[1][2]。该方法通过提取器官、病灶区域等目标组织的本质特征，为临床诊断和病理研究提供可靠依据。然而，特定器官和病灶区域的标注过程存在耗时费力、效率低下等问题，需要专业人员参与完成[3][4]。由于数据集稀缺、定位标注困难等突出问题[5]，医学图像分割任务变得尤为复杂。因此，该领域广泛探索如何运用计算机视觉技术构建精准且高鲁棒性的医学图像分割系统，以应对数据匮乏、标注精度等复杂挑战[6][7][8]。

​ 凭借卓越的特征提取能力，卷积神经网络（CNN）近年来在医学图像分割应用中取得显著成就[9][10][11]。例如U-Net[12]、3D-UNet[10]、ResUNet[13]、UNet++[14]和DenseUNet[15]在精细医疗任务中的多器官分割方面表现优异。尽管基于CNN的网络具备出色的分割能力，但由于卷积操作感受野的固有局限，这些网络难以建立特征信息间的全局依赖关系，导致远程语义信息交互受阻，上下文特征提取不充分。研究者虽通过注意力机制[16]、金字塔模型[17]等技术试图扩大CNN的感受野以获取全局信息，但这些操作需要叠加多层卷积并持续下采样，随着网络深度增加可能引发梯度消失/爆炸问题，造成局部信息丢失，尤其在小数据集场景下带来训练挑战[18]。

​ 为弥补卷积在长程依赖建模的不足，研究者将自然语言处理（NLP）领域的Transformer技术引入计算机视觉领域[19][20]。该技术通过独特的自注意力机制根据输入内容动态调整感受野[21][22]，在获取全局语义信息方面优于卷积操作。例如Dosovitskiy等[20]采用Transformer进行图像识别，效果可比肩当时最先进（SOTA）技术。为建立局部连接并解决视觉2元素尺度变化问题，Liu等[23]提出基于移位窗口多头自注意力（SWMSA）的分层Swin Transformer。然而，Transformer虽擅长捕捉全局语义依赖，却在封装细节特征和长序列计算效率方面存在局限。近期Mamba[24]及其变体[25][26]通过结合结构化状态空间模型（SSM）与Transformer的MLP机制，能沿序列维度选择性传递/遗忘信息，提升了长序列计算效率。但与Transformer显式注意力机制相比，此类方法的SSM机制处理长程依赖时缺乏直观性，在密集分割任务中性能受限。

​ 最新研究尝试融合CNN与Transformer以发挥各自优势，从而有效缓解单一模块的局限性[2][27][28][29]。当前主流医学图像分割技术多采用U型编解码设计，虽取得显著成功，但分割性能仍有优化空间，主要因为编码与解码阶段间的语义鸿沟未得到全面解决[2][23][30]。存在语义鸿沟时，由于深层特征对目标识别与浅层特征对边缘分割的双重重要性，特征融合将面临挑战[31]。

综上所述，本研究提出名为MixFormer的新型CNN-Transformer混合主干网络用于医学图像分割。该框架不仅解决了上述挑战，更在多项评估指标上超越现有最优方法。本文的主要创新与贡献可归纳如下：

1. 先进MixFormer架构：混合编码器网络在下采样过程的每个尺度上，创新性地融合了Transformer的全局上下文信息与CNN的局部细节特征，实现二者的协同增强。
2. 多尺度空间感知融合（MSAF）模型：通过智能整合不同尺度共识区域的信息，确保粗粒度与细粒度特征表征间的语义一致性，有效捕捉跨尺度特征依赖关系。
3. 混合多分支空洞注意力（MMDA）机制：在跳跃连接步骤中引入该机制，既能过滤冗余语义信息，又可强化关键语义特征，显著缩小编码器与解码器间的特征语义鸿沟。
4. 实验验证：在五大主流医学图像分割数据集上的测试表明，MixFormer具有卓越的效能与泛化能力。实验结果清晰证明，该模型在分割性能上持续超越现有最先进模型。

II. RELATED WORK

本节综述了医学图像分割领域的相关研究进展，涵盖基于Transformer和CNN的两大类分割技术，并简要探讨了多尺度结构在医学图像分割中的作用。

A. CNN-Based Segmentation Networks

​ 随着深度学习的演进，图像分割领域涌现出众多基于CNN的经典网络。全卷积网络（FCN）的出现显著加速了分割网络的发展进程[32]，但其分割结果往往较为粗糙。针对这一局限，Ronneberger等人[12]提出性能更优的U-Net网络，通过采用能捕获更丰富特征的U型编解码结构，显著提升了分割精度。此后，研究者们致力于改进U型编解码架构[图1(a)]以获得更精细的结果。例如Li等人[15]采用DenseNet模块构建U型结构网络，结合二维与三维切片信息生成更具鲁棒性的特征表征；UNet 3+[33]通过聚合多尺度特征来优化特征表达。尽管现有创新工作已部分解决了CNN的局限性，但上下文依赖关系的捕捉仍是挑战，卷积操作的固有缺陷可能导致医学图像的欠分割与过分割现象。

B. Transformer-Based Segmentation Networks

​ 视觉Transformer（ViT）凭借其出色的长程依赖建模能力，在计算机视觉领域引发了巨大反响[20]。然而，为达到预期效果，Transformer需首先在海量数据上进行训练。Touvron等人[40]提出一种训练方法与知识蒸馏技术，使ViT即使在小数据集上也能高效运行，有效克服了这一局限。此外，为缓解ViT中多头自注意力机制（MSA）带来的计算负担，Liu等人[23]提出Swin Transformer。这种基于SW-MSA的分层ViT在局部窗口内执行自注意力运算，既解决了输入数据的大尺度变化问题，又显著提升了计算性能。

​ 针对Transformer获取局部细节信息不足的缺陷，研究者提出了TransUNet[2]。该方法将Transformer与CNN相结合，通过U-Net结构同步获取全局语义与局部特征。其他先进的基于Transformer的分割网络还包括TransFuse[29]、MedT[41]、脑肿瘤分割专用Transformer（TransBTS）[42]以及UNEt Transformer（UNETR）[43]。

C. Multiscale Architectures for Medical Image Segmentation

​ 多尺度语义信息在图像分割中是一项至关重要的技术[44]。以往的大多数研究都利用卷积神经网络（CNN）或Transformer进行多尺度特征提取。然而，这些方法固有的缺陷通常会导致特征映射效果不佳，缺乏显著信息。在基于CNN的图像分割方法中，金字塔场景解析网络（PSPNet）[16]通过引入金字塔池化模块（PPM）实现了多尺度特征提取，该模块使用不同大小的池化核对输入特征图进行分层池化，以从不同子区域提取特征。UNet++[14]和UNet 3+[33]则通过简单的跳跃连接充分利用了多尺度信息。在基于Transformer的图像分割方法中，MedT[41]通过两个分支结合长距离依赖和局部依赖来提取多尺度特征，而SwinPA-Net[45]则通过密集乘法特征融合级联多尺度语义特征信息，以减少浅层背景噪声的干扰。具体而言，这些方法的缺陷可归因于两个关键障碍：1）它们无法在保持特征一致性的同时无缝集成低级和高级语义特征；2）它们提取分层编码器生成的多尺度信息的能力不足。受多尺度特征表示的启发，我们提出了MixFormer，这是一种基于CNN-Transformer的混合架构网络，能够保持多尺度特征的多样性和一致性。

III. METHOD

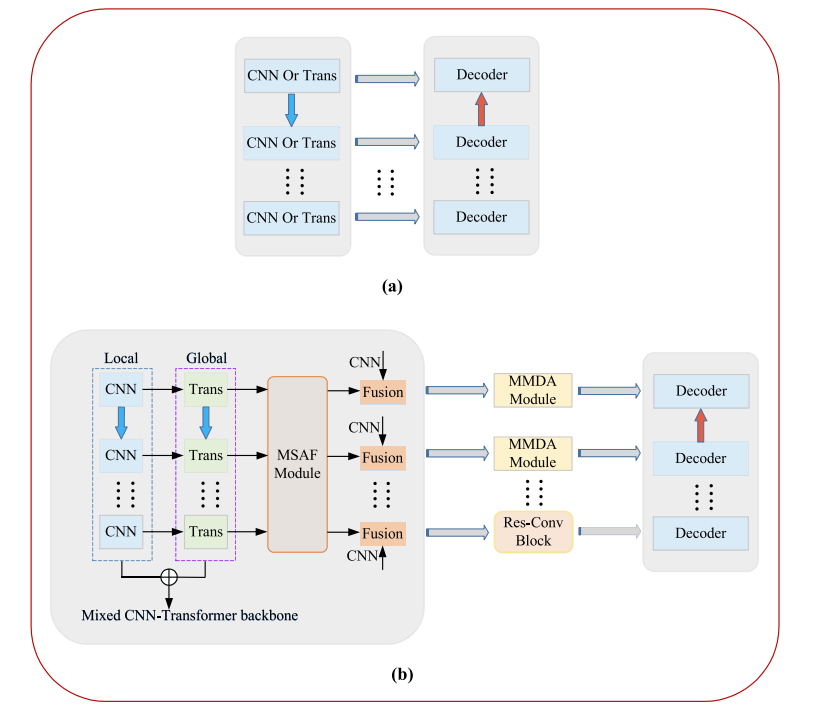
图1。（a）典型医学图像分割网络的结构。（b）所提出的MixFormer网络示意图。此外，Trans代表基于Transformer的架构。MSAF、Res-Conv和MMDA模型是我们所提方法中使用的模块。

图2. 所提出的MixFormer概述。在解码器的跳跃连接部分，MMDA模块被用于抑制冗余的语义信息，同时增强有价值的语义特征，并缓解采样过程造成的信息损失。此外，MSAF模块被用于充分提取由分层编码器生成的多尺度信息。

A. Network Structure

​ 所提出的MixFormer采用了典型的U形架构，该架构主要由编码器、解码器和跳跃连接组成[如图1(b)所示]。该方法的全局框架如图2所示。编码器包含两部分：基于CNN-Transformer的混合特征提取主干网络和一个多尺度注意力融合（MSAF）模型。解码器则由基本的卷积神经网络（CNN）单元构成。此外，在跳跃连接部分引入了一个混合多分支空洞注意力（MMDA）模块。在该方法中，混合特征提取器用于从Transformer和CNN中分别获取包含全局和局部线索的多层视觉特征。MSAF机制进一步与多尺度语义信息进行交互，以获得增强的特征表示。为了实现更优的上采样性能，我们在编码器的最深层实施了残差卷积（Res-Conv）块，以进一步加强全局特征表示。最后，我们将MMDA机制集成到跳跃连接中，有效地将融合后的语义特征传输到解码器，以进行最终的分割预测。

B. Mixed Feature Extraction Backbone

​ 在所提出的MixFormer中，我们采用了一种混合编码器框架，该框架由Swin Transformer和Res2Net50[46]组成，用于在编码阶段提取特征。这种设计使得编码器能够在每个尺度上有效地捕捉局部细节和全局上下文信息。与传统的卷积神经网络（CNN）相比，Res2Net50在提取多尺度特征方面表现更优。此外，Swin Transformer在定义好的窗口内对图像块执行自注意力计算，其计算开销随图像大小呈线性增长，这与视觉Transformer（ViT）在整个图像块集合上进行自注意力计算的方式形成了鲜明对比。

1. Res2Net50 Model:

​ 标准卷积核只能从给定图像中提取相同尺度的特征，因此需要构建不同大小的卷积核以获取多尺度特征。Gao等人[46]提出了Res2Net，该模型专门设计用于获取多尺度特征图。对于包括ResNet和ResNeXt[47]在内的许多卷积神经网络(CNN)架构而言，瓶颈块(bottleneck block)是基本组件。Res2Net寻求一种替代设计，在保留与瓶颈块相当的计算负担的同时，具备更强大的多尺度特征提取能力。Res2Net块与瓶颈块之间的差异如图3所示。

​ 具体而言，在经过1×11\times11×1卷积之后，输入特征图被均匀地分割成SSS个子集，用xix_ixi表示，其中i∈{1,2,...,S}i\in\{1,2,\ldots,S\}i∈{1,2,...,S}。与输入特征图不同的是，每个子集xix_ixi具有相同的空间大小，但通道数仅为原来的1/S (除了x1x_{1}x1)。对于每个xix_ixi (i≠1i\neq1i=1 ),都对应一个由 Ki(⋅)K_i(\cdot)Ki(⋅)表示的3×33\times33×3卷积操作。Ki(⋅)K_i(\cdot)Ki(⋅)的结果用符号yiy_iyi表示。然后，将yi−1y_i-1yi−1(此处原文yi−1(⋅)y_i-1(\cdot)yi−1(⋅)应理解为yi−1y{i-1}yi−1,因为yi−1y_{i-1}yi−1 是前一个卷积操作的结果，而非函数)与子集 xix_ixi 相结合，再输入到Ki(⋅)K_i(\cdot)Ki(⋅)中。因此，yiy_iyi可以表示为以下形式：
yi={xi,i=1Ki(xi),i=2Ki(xi+yi−1),2<i≤S. y_i = \begin{cases} x_i, & i = 1 \\ K_i(x_i), & i = 2 \\ K_i(x_i + y_{i-1}), & 2 < i \leq S. \end{cases} yi=⎩ ⎨ ⎧xi,Ki(xi),Ki(xi+yi−1),i=1i=22<i≤S.

​ 在本研究中，我们利用Res2Net50网络作为局部细节提取器，对原始图像(尺寸为H×WH\times WH×W)进行有效分割，以获得不同分辨率下的特征金字塔输出F1F_1F1-F4F_4F4。随后，通过1×11\times11×1卷积操作，将这些输出的通道维度映射到与相应Swin Transformer块相同的嵌入维度。接下来，将它们输入到Swin Transformer模块中，以此作为对Res2Net 模型的补充，因为Res2Net模型在不同阶段会遗漏长距离依赖关系。在我们的方法中，共有四个下采样阶段用于获取局部语义信息。每个阶段输出的特征图尺寸分别为H/4×W/4H/4\times W/4H/4×W/4、H/8×W/8H/8\times W/8H/8×W/8、H/16×W/16H/16\times W/16H/16×W/16和H/32×W/32H/32\times W/32H/32×W/32,对应的通道数分别为DDD、2DDD、4DDD和8DDD。

2. Swin Transformer Model:

​ 如图4所示，视觉Transformer（ViT）对整体嵌入的图像块执行自注意力计算。在典型的多头自注意力（MSA）模块中，一个主要问题是其计算复杂度是图像空间维度的二次函数。为了缓解这一限制，Swin Transformer[23]引入了窗口多头自注意力（W-MSA）和移位窗口多头自注意力（SW-MSA）技术。图5(b)展示了两个连续的Swin Transformer块，每个块都包含层归一化（LayerNorm，LN）层、MSA模块、多层感知机（MLP）层和残差连接。此外，两个相邻的MSA块被替换为W-MSA块和SW-MSA块。W-MSA的计算开销与图像大小呈线性相关，因为它在定义好的窗口内执行自注意力计算。然而，由于这些窗口之间缺乏信息交换，其建模长距离依赖关系的能力受到限制。相比之下，SW-MSA引入了一种循环移位操作，将每个窗口向左上方向移动。这一策略性步骤使得各种不相邻的子窗口能够高效地相互交互。因此，Swin Transformer能够有效地建模上下文依赖关系，并获取高效的层次化特征表示。

​ 在Swin Transformer中，输入特征图被划分为不重叠的窗口，每个窗口包含M×MM\times MM×M(本文中设置为7)个图像块。作为 (移位)窗口多头自注意力 ((S)W-MSA)的输入，Zl−1∈RL×D\mathbf{Z}^{l-1}\in\mathbb{R}^{L\times D}Zl−1∈RL×D 是一个长度为LLL、维度为DDD的图像块序列。基于这种窗口划分策略，Swin Transformer块的输入和输出可以表示为：
Z^l=W-MSA(LN(Zl−1))+Zl−1 \hat{\mathbf{Z}}^l=\text{W-MSA}\left(\mathrm{LN}(\mathbf{Z}^{l-1})\right)+\mathbf{Z}^{l-1} Z^l=W-MSA(LN(Zl−1))+Zl−1

Zl=MLP(LN(Z^l))+Z^l \mathbf{Z}^{l} = \text{MLP}(\text{LN}(\hat{\mathbf{Z}}^{l})) + \hat{\mathbf{Z}}^{l} Zl=MLP(LN(Z^l))+Z^l

Z^l+1=SW-MSA(LN(Zl))+Zl \hat{\mathbf{Z}}^{l+1}=\text{SW-MSA}\left(\mathrm{LN}(\mathbf{Z}^l)\right)+\mathbf{Z}^l Z^l+1=SW-MSA(LN(Zl))+Zl

Zl+1=MLP(LN(Z^l+1))+Z^l+1 \mathbf{Z}^{l+1}=\mathrm{MLP}\big(\mathrm{LN}(\hat{\mathbf{Z}}^{l+1})\big)+\hat{\mathbf{Z}}^{l+1} Zl+1=MLP(LN(Z^l+1))+Z^l+1

​ 其中，Z^l\hat{Z}^lZ^l和ZlZ^lZl分别表示第ι\iotaι个块的窗口多头自注意力 (W-MSA) 和多层感知机 (MLP) 的输出。类似地Z^l+1\hat{\mathbf{Z}}^{l+1}Z^l+1和Zl+1\mathbf{Z}^{l+1}Zl+1分别表示第(l+1)(l+1)(l+1)个块的移位窗口多头自注意力 (SW-MSA) 和多层感知机 (MLP)的结果。LN(-) 表示层归一化操作符。根据之前的研究工作[20],[23],自注意力计算方式如下：
Q=zlWQ,K=zlWK,V=zlWV Q = z^l \mathbf{W}_Q, \quad K = z^l \mathbf{W}_K, \quad V = z^l \mathbf{W}_V Q=zlWQ,K=zlWK,V=zlWV

Attention(Q,K,V)=SoftMax(QKTd+B)V \text{Attention}(Q,K,V)=\text{SoftMax}{\left(\frac{QK^T}{\sqrt{d}}+B\right)}V Attention(Q,K,V)=SoftMax(d QKT+B)V

​ 其中，QQQ、KKK和V∈RL×dV\in\mathbb{R}^{L\times d}V∈RL×d分别代表查询 (query)、键 (key)和值 (value)矩阵；ddd表示查询或键的维度。WQ、WK\mathbf{W}_Q、\mathbf{W}_KWQ、WK和WV∈RD×d\mathbf{W}_V\in\mathbb{R}^{D\times d}WV∈RD×d代表三个投影矩阵的可学习参数。此外，B∈RL×LB\in\mathbb{R}^L\times LB∈RL×L表示偏置矩阵。

​ 为了弥补Res2Net模型中缺失的全局上下文信息，我们将局部细节特征图Fi(i=1,2,3,4)F_i(i=1,2,3,4)Fi(i=1,2,3,4)划分为图像块，并将其输入到Swin Transformer中。Swin Transformer包含四个阶段，每个阶段都有特定数量的块，这使得模型能够建模长距离依赖关系。通过这种方式，我们能够推导出四个阶段的特征表示S1−S4S_1-S_4S1−S4 ,这些表示包含了全局上下文信息。此外，我们在每个阶段采用了块合并(patch merging)方法，将特征图Sj(j=1,2,3)S_j(j=1,2,3)Sj(j=1,2,3)的通道维度加倍，同时降低分辨率，然后将处理后的特征图输入到下一阶段的Swin Transformer块中。Swin Transformer中四个阶段的特征图分辨率分别为H/4×W/4H/4\times W/4H/4×W/4、H/8×W/8H/8\times W/8H/8×W/8、H/16×W/16H/16\times W/16H/16×W/16和H/32×W/32H/32\times W/32H/32×W/32,对应的通道数分别为D′D^{\prime}D′、2D′D^{\prime}D′、4D′D^{\prime}D′和 8D′D^{\prime}D′。

​ 最后，我们将局部空间信息FiF_iFi (i=1,2,3,4)i=1,2,3,4)i=1,2,3,4)和全局语义信息SjS_jSj (j=1,2,3,4)j=1,2,3,4)j=1,2,3,4)在相应层级进行连接，以获取四个尺度上的增强特征表示L1−L4L_1-L_4L1−L4。然后，将这些特征表示输入到多尺度注意力融合(MSAF)模型中，以实现不同尺度之间的信息通信。

C. MSAF Model

​ 已有研究表明，多尺度信号在分割位置复杂且大小各异的器官时极具价值。为了应对多尺度特征间语义信息交互的挑战，我们利用了多尺度注意力融合 (MSAF) 模块的功能。该模块针对编码后的特征包含四个步骤：块匹配(patch matching)、尺度融合 (scale fusing)、尺度分离 (scale splitting) 和块逆变换 (patch inversing),这些步骤共同实现了跨尺度依赖关系的建立。该MSAF模块的网络结构如图6所示。

​ 具体而言，我们首先通过下采样操作，将所有特征图规范化为相同的通道维度D′D^{\prime}D′ [图6(a)],并将它们分配到具有相同颜色(即红色)的对应边界框中。具体来说，我们首先将所有特征图规范化为相同的通道维度D′D^{\prime}D′[图6(a)], 然后通过下采样操作将它们分配到对应颜色(如红色)的边界框中。若将pjip_j^ipji视为第iii个尺度上的第jjj个块，则pji+1p_j^{i+1}pji+1 、pji+2p_j^{i+2}pji+2 和pji+3p_j^{i+3}pji+3 即为与之匹配的下采样块。通过这一步骤，我们能够从第 iii个尺度到第(i+3)\left(i+3\right)(i+3) 个尺度的四个连续特征映射中定位到相关的空间感知块，同时保留最相关块之间的空间对应关系。

​ 然后，我们通过尺度融合（scale fusing）的方法，将不同尺度上空间相关的块进行聚合，以生成一系列的标记（tokens）。这一过程可以描述如下：

flatten⁡(pj1),...,flatten⁡(pjN)\]→pjcat \\left\[\\operatorname{flatten}\\left(p_{j}\^{1}\\right), \\ldots, \\operatorname{flatten}\\left(p_{j}\^{N}\\right)\\right\] \\rightarrow p_{j}\^{\\text {cat }} \[flatten(pj1),...,flatten(pjN)\]→pjcat ​ 其中，flatten(·) 表示拼接（concatenation）操作。由于这一系列标记（tokens）缺乏二维空间信息，我们利用Transformer块来确保它们空间结构的一致性。图像块之间空间感知的跨尺度依赖关系可以通过以下公式获得： p\~jcat=W-MSA(LN(pjcat))+pjcat \\tilde{\\boldsymbol{p}}_j\^\\mathrm{cat}=\\text{W-MSA}\\left(\\mathrm{LN}(\\boldsymbol{p}_j\^\\mathrm{cat})\\right)+\\boldsymbol{p}_j\^\\mathrm{cat} p\~jcat=W-MSA(LN(pjcat))+pjcat p\^jcat=MLP(LN(p\~jcat))+p\~jcat \\widehat{\\boldsymbol{p}}_j\^{\\mathrm{cat}}=\\mathrm{MLP}(\\mathrm{LN}(\\tilde{\\boldsymbol{p}}_j\^{\\mathrm{cat}}))+\\tilde{\\boldsymbol{p}}_j\^{\\mathrm{cat}} p jcat=MLP(LN(p\~jcat))+p\~jcat pˉjcat=SW-MSA(LN(p\^jcat))+p\^jcat \\bar{\\boldsymbol{p}}_j\^\\mathrm{cat}=\\text{SW-MSA}\\left(\\mathrm{LN}(\\widehat{\\boldsymbol{p}}_j\^\\mathrm{cat})\\right)+\\widehat{\\boldsymbol{p}}_j\^\\mathrm{cat} pˉjcat=SW-MSA(LN(p jcat))+p jcat p\^jcat=MLP(LN(pˉjcat))+pˉjcat. \\hat{p}_j\^{\\mathrm{cat}}=\\mathrm{MLP}(\\mathrm{LN}(\\bar{p}_j\^{\\mathrm{cat}}))+\\bar{p}_j\^{\\mathrm{cat}}. p\^jcat=MLP(LN(pˉjcat))+pˉjcat. ​ 接下来，我们采用尺度分离（scale splitting）的方法，按照拼接顺序将所得到的增强序列逆变换回图像块。这一操作可通过以下公式表示： Inverse(Split(p\^jcat))→p\^j1,...,p\^jN \\mathrm{Inverse}(\\mathrm{Split}(\\hat{\\boldsymbol{p}}_{j}\^{{\\mathrm{cat}}}))\\to\\hat{\\boldsymbol{p}}_{j}\^{1},\\ldots,\\hat{\\boldsymbol{p}}_{j}\^{N} Inverse(Split(p\^jcat))→p\^j1,...,p\^jN ​ 其中，Split(·) 操作是 flatten(·) 操作的逆过程。最后，块逆变换（patch inversion）将同一尺度下的所有图像块合并为增强特征图 P1--P4，这些增强特征图与卷积神经网络（CNN）特征金字塔的输出 F1--F4 进行融合，并通过跳跃连接（skip connections）进一步输入到解码器阶段。 #### D. Mixed Multibranch Dilated Attention Model ​ 神经网络中浅层和深层特征层所包含的表示能力各不相同。因此，迫切需要找到一种解决方案，以高效地弥合编码阶段和解码阶段对应特征之间的语义鸿沟，同时尽量减少由采样过程引发的信息损失。在此，我们引入了一种混合多分支空洞注意力（Mixed Multibranch Dilated Attention, MMDA）模型，该模型从通道（channel）、空间（spatial）和全局上下文（global contextual）三个维度对特征进行映射，综合优化提取特征的信息损失。这种方法有效地减少了提取特征中的信息损失，从而帮助解码器准确地恢复特征图的原始分辨率。我们将从MSAF的每一层（除最深层的下采样层外）提取的特征图与对应的卷积神经网络（CNN）特征金字塔输出进行融合。随后，这种组合输入通过跳跃连接被送入MMDA模块进行特征提取。最终，这种方法实现了与对应解码器层的和谐特征融合。MMDA模型由三个单元组成，包括全局自注意力单元（global self-attention unit）、通道注意力单元（channel attention unit）和空间注意力单元（spatial attention unit），如图7所示。 ​ 通道注意力单元(图7中的第一部分)主要获取图像的纹理信息，同时关注各通道特征之间的交互。对于给定的输入特征图F∈RC×H×WF\\in\\mathbb{R}\^{C\\times H\\times W}F∈RC×H×W ,通过最大池化 (MaxPooling)和平均池化 (AvgPooling)操作沿空间轴提取特征信息。得到的特征图C\^M∈RC×1×1\\hat{C}_M\\in\\mathbb{R}\^{C\\times1\\times1}C\^M∈RC×1×1和CA∈RC×1×1C_A\\in\\mathbb{R}\^{C\\times1\\times1}CA∈RC×1×1分别经过1×11\\times11×1卷积和 LeakyReLU 激活函数处理，然后进行逐元素的加法操作。最后，使用 Siqmoid 函数得到通道注意力图。具体流程如下： CM=LeakyReLU{Conv\[MaxPool(F)\]} C_M = \\text{LeakyReLU}\\{\\text{Conv}\[\\text{MaxPool}(F)\]\\} CM=LeakyReLU{Conv\[MaxPool(F)\]} CA=LeakyReLU{Conv\[AvgPool(F)\]} C_A=\\text{LeakyReLU}\\{\\mathrm{Conv}\[\\mathrm{AvgPool}(F)\]\\} CA=LeakyReLU{Conv\[AvgPool(F)\]} C(F)=Sigmoid(CM⊕CA), C(F)∈RC×1×1 C(F) = \\text{Sigmoid}(C_M \\oplus C_A), \\ C(F) \\in \\mathbb{R}\^{C \\times 1 \\times 1} C(F)=Sigmoid(CM⊕CA), C(F)∈RC×1×1 ​ 其中，C(F)C(F)C(F)表示通道注意力图，⊕\\oplus⊕表示逐像素相加 (pixel-by-pixel summation) 。 空间注意力单元 (图7中的第二部分)的主要目标是识别网络中最重要的区域，以便进行进一步的处理。受先前使用坐标注意力 (Coordinate Attention,CA)\[48\]模块的研究启发，我们采用CA技术作为MMDA模型的空间注意力部分，以利用精确的空间位置信息对特征表示进行编码。该方法分为两个子步骤：坐标信息嵌入(coordinate information embedding) 和CA生成 (CA generation)。具体而言，给定一个特征图F∈RC˘×H×WF\\in\\mathbb{R}\^{\\breve{C}\\times H\\times W}F∈RC˘×H×W,首先使用尺寸为(H,1)\\left(H,1\\right)(H,1)或(1,W)\\left(1,W\\right)(1,W)的池化核，分别沿水平和垂直坐标对每个通道进行编码。因此， 双向坐标信息嵌入的输出如下： FH=Avgpool(H,1)(F),FH∈RC×H×1 F_H=\\mathrm{Avgpool}_{(H,1)}(F),\\quad F_H\\in\\mathbb{R}\^{C\\times H\\times1} FH=Avgpool(H,1)(F),FH∈RC×H×1 FW=Avgpool(1,W)(F),FW∈RC×1×W. F_W=\\mathrm{Avgpool}_{(1,W)}(F),\\quad F_W\\in\\mathbb{R}\^{C\\times1\\times W}. FW=Avgpool(1,W)(F),FW∈RC×1×W. ​ 在CA (坐标注意力)生成步骤中，首先将两个特征图(FHF_HFH 和 FWF_WFW)进行拼接，然后使用共享的1×1\\times1×1卷积算子生成一个包含水平和垂直方向空间信息的中间特征图fff。具体操作可通过以下公式表示： f=δ(BN(Conv(Cat(FH,FW)))),f∈RC/r×1×(H+W) f=\\delta(\\mathrm{BN}(\\mathrm{Conv}(\\mathrm{Cat}(F_H,F_W)))),\\quad f\\in\\mathbb{R}\^{C/r\\times1\\times(H+W)} f=δ(BN(Conv(Cat(FH,FW)))),f∈RC/r×1×(H+W) ​ 其中，δ(⋅)\\delta(\\cdot)δ(⋅)表示非线性激活函数，BN 表示批归一化 (batch normalization) 操作。缩减比率rrr通常用于降低 模型的计算复杂度(例如，设为16)。接下来，我们沿着空间维度将中间特征图fff分割成两个独立的特征表示，即fHf_HfH和fWf_WfW。然后，利用两个1×11\\times11×1卷积操作将它们转换为与输入特征图FFF相同通道数的特征表示。具体操作可通过以下公式表示： fH=Split(f)H,fH∈RC/r×H×1 f_H=\\mathrm{Split}(f)_H,\\quad f_H\\in\\mathbb{R}\^{C/r\\times H\\times1} fH=Split(f)H,fH∈RC/r×H×1 fW=Split(f)W,fW∈RC/r×W×1 f_W=\\mathrm{Split}(f)_W,\\quad f_W\\in\\mathbb{R}\^{C/r\\times W\\times1} fW=Split(f)W,fW∈RC/r×W×1 SH=Sigmoid(Conv(fH)),SH∈RC×H×1 S_H=\\mathrm{Sigmoid}(\\mathrm{Conv}(f_H)),\\quad S_H\\in\\mathbb{R}\^{C\\times H\\times1} SH=Sigmoid(Conv(fH)),SH∈RC×H×1 SW=Sigmoid(Conv(fW)),SW∈RC×1×W S_W=\\mathrm{Sigmoid}(\\mathrm{Conv}(f_W)),\\quad S_W\\in\\mathbb{R}\^{C\\times1\\times W} SW=Sigmoid(Conv(fW)),SW∈RC×1×W ​ 其中，SHS_HSH 和 SWS_WSW 随后被扩展并分别用作注意力权重。最终，坐标注意力 (CA) 模块的结果可以表示为： S(F)=F×SH×SW,S(F)∈RC×H×W S(F)=F\\times S_H\\times S_W,\\quad S(F)\\in\\mathbb{R}\^{C\\times H\\times W} S(F)=F×SH×SW,S(F)∈RC×H×W ​ 其中，S(F)S(F)S(F)表示最终的空间注意力图。 ​ 全局注意力单元(图7中的第三部分)利用 Swin Transformer\[23\] 的块结构 来构建全局上下文依赖之间的相关性。这一操作能够弥补空间注意力单元和通道注意力单元所带来的信息损失。首先，将输入特征图F∈RC×H×WF\\in\\mathbb{R}\^{C\\times H\\times W}F∈RC×H×W 分割成一系列图像块 (patches) 。由于这些图像块之间不存在二维空间结构信息，因此需要将它们输入到 (移位)窗口多头自注意力机制 ((S)W-MSA) 中，以计算图像块之间的相似性表示关系，并从中恢复位置信息。最后，将增强后的特征序列转换为一个全局注意力图G(F)∈RC×H×WG(F)\\in\\mathbb{R}\^{C\\times H\\times W}G(F)∈RC×H×W。这一步骤的详细信息可在(2)中找到。 ​ 最后，我们将空间注意力图S(F)S(F)S(F)和通道注意力图C(F)C(F)C(F)相乘，并进一步加上全局注意力图G(F)G(F)G(F),以得到混合 多分支空洞注意力图 MMDA(F)∈RC×H×W.(F)\\in\\mathbb{R}\^{C\\times H\\times W}.(F)∈RC×H×W. MMDA(F)=\[S(F)⊗C(F)\]⊕G(F) \\mathrm{MMDA}(F)=\[S(F)\\otimes C(F)\]\\oplus G(F) MMDA(F)=\[S(F)⊗C(F)\]⊕G(F) ​ 其中，⊗\\otimes⊗ 表示使用Python广播机制进行的乘法运算，⊕\\oplus⊕ 表示逐元素的加法运算。 #### E. Decoder ​ 为了增强有效感受野，并使其更易于融合远距离的上下文信息，我们将融合后的特征图输入到下采样过程中最深层的残差卷积 (Res-Conv) 块中。如图2所示，Res-Conv块由LLL层组成(在本研究中，LLL被设置为7),该块通过深度卷积(即卷积核大小k=7k=7k=7)和逐点卷积(即卷积核大小k=1k=1k=1)混合空间位置和通道位置，从而进一步获取上下文依赖关系。此外，深度卷积中的分组通道数等于输入特征图的通道数，并且对每个卷积操作都应用了高斯误差线性单元(GeLU)激活函数和批归一化处理，如下列公式所示： fl′=BN(σ1{DepthwiseConv(fl−1)})+fl−1 f_{l}\^{\\prime} = \\mathrm{BN}(\\sigma_{1}\\{\\mathrm{DepthwiseConv}(f_{l-1})\\}) + f_{l-1} fl′=BN(σ1{DepthwiseConv(fl−1)})+fl−1 fl=BN(σ1{PointwiseConv(fl′)}) f_l=\\mathrm{BN}(\\sigma_1\\{\\text{PointwiseConv}(f_l\^{\\prime})\\}) fl=BN(σ1{PointwiseConv(fl′)}) 以及在保持令人满意的网络性能的同时降低计算复杂度。 ​ 最后，我们采用双线性插值方法对特征图进行上采样。解码器由四个阶段组成，每个阶段包括一个典型的 3×33 \\times 33×3 卷积块、一个 2×22 \\times 22×2 上采样操作和修正线性单元 (ReLU) 激活函数。解码器首先接收低分辨率 (H/32×W/32)(H/32 \\times W/32)(H/32×W/32) 的融合特征图，并在经过四次连续上采样操作后生成高分辨率 (H×W)(H \\times W)(H×W) 的特征图。然后，将重建的特征图通过分割头中的一个 3×33 \\times 33×3 卷积，生成最终的分割结果，其中通道数与预测类别的数量相同。 ​ 其中，fif_ifi 表示 Res-Conv 块中第 iii 层的输出特征图，σi\\sigma_iσi 表示 GeLU 激活函数，BN 表示批归一化。DepthwiseConv 和 PointwiseConv 代表深度可分离卷积 \[49\] 的两个主要阶段，其网络架构如图8所示。 ​ 在 DepthwiseConv 阶段（图8的(a)部分），每个卷积核被指定用于处理输入图像的单个通道，生成与输入通道数匹配的中间特征图。例如，当处理一个 5×5×35 \\times 5 \\times 35×5×3 的彩色图像时，此过程会生成三个大小为 5×5×35 \\times 5 \\times 35×5×3 的中间特征图。然而，这种每个通道独立进行卷积的方法未能充分利用通道间特征的相关性。因此，它忽略了同一空间位置上通道之间的有价值信息交互。为了解决这一限制并获得最终的输出特征图，PointwiseConv 阶段（图8的(b)部分）是一个关键操作。这里使用了大小为 1×1×C1 \\times 1 \\times C1×1×C 的卷积核，其中 CCC 表示前一层特征图的通道数。通过 PointwiseConv 过程，每个核沿通道维度组合中间特征图，以有效地生成新的特征图。这种方法显著减少了参数数量和计算复杂度，同时保持了令人满意的网络性能。 ​ 最后，我们采用双线性插值方法对特征图进行上采样。解码器由四个阶段组成，每个阶段包括一个典型的 3×33 \\times 33×3 卷积块、一个 2×22 \\times 22×2 上采样操作和修正线性单元 (ReLU) 激活函数。解码器首先接收低分辨率 (H/32×W/32)(H/32 \\times W/32)(H/32×W/32) 的融合特征图，并在经过四次连续上采样操作后生成高分辨率 (H×W)(H \\times W)(H×W) 的特征图。然后，将重建的特征图通过分割头中的一个 3×33 \\times 33×3 卷积，生成最终的分割结果，其中通道数与预测类别的数量相同。 #### F. Total Loss