在二分类问题中,SVM(支持向量机)未采用0/1 损失函数 ,而是选择 Hinge 损失等替代损失函数,核心原因在于0/1 损失函数的优化不可行性 与SVM 的优化目标(最大化间隔)不匹配。要理解这一点,需从两类损失函数的本质特性、优化难度及 SVM 的设计逻辑三方面展开分析:
一、先明确:0/1 损失函数的 "理想性" 与 "缺陷"
0/1 损失函数是二分类任务的 "理想损失"------ 它直接衡量模型预测结果与真实标签的 "对错",定义如下(假设标签y∈{+1,−1},模型输出h(x)为预测分数):

其核心优势是 "直观贴合任务目标",但缺陷却使其无法直接用于 SVM 的优化:
1. 非凸、非连续:优化陷入 "NP 难"
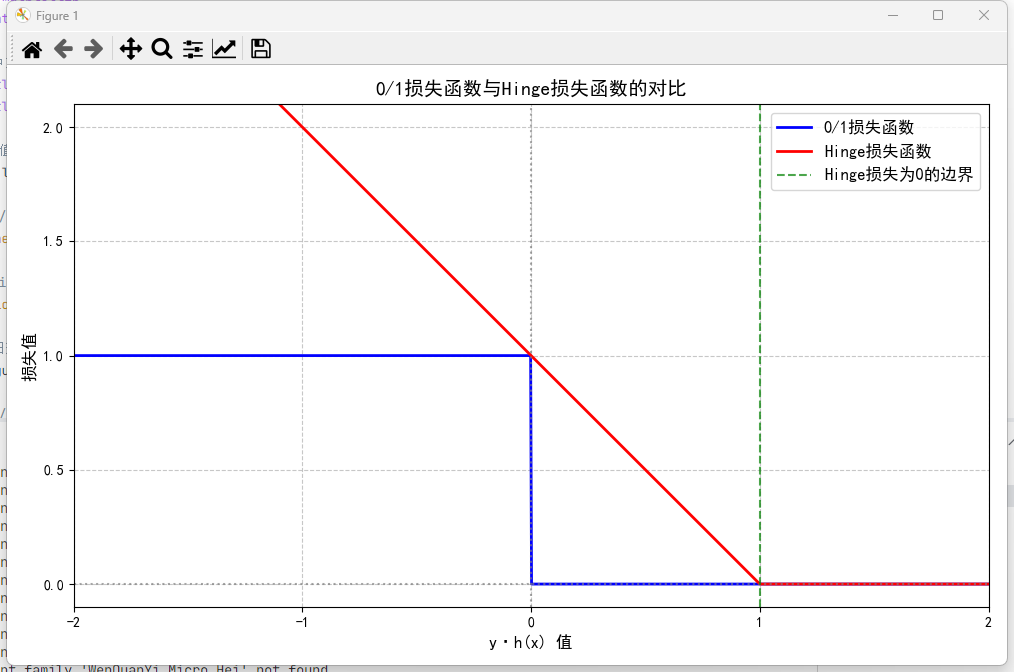
0/1 损失函数是阶跃函数------ 在y⋅h(x)=0(决策边界)处发生不连续跳跃,且整个函数图像无 "凸性"(凸函数的局部最优即全局最优,是梯度下降等优化算法的基础)。
- 非连续性导致无法计算梯度:梯度优化算法(如 SGD、牛顿法)依赖函数的导数 / 梯度指引更新方向,0/1 损失的阶跃处导数不存在,算法无法推进;
- 非凸性导致优化陷入局部最优:即使强行搜索,也难以找到全局最小损失,最终模型性能不稳定(可能停留在 "错误率稍低但间隔极小" 的局部最优)。
2. 仅关注 "对错",忽略 "置信度":与 SVM 目标冲突
SVM 的核心设计目标是最大化分类间隔 (即决策边界到两类样本的最小距离)------ 间隔越大,模型泛化能力越强(对噪声、异常值更鲁棒)。
但 0/1 损失仅判断 "是否正确",不关心 "正确 / 错误的程度":
- 例如,一个样本在决策边界右侧 10 个单位(高置信度正确),与在右侧 0.1 个单位(低置信度正确),在 0/1 损失中均计为 0;
- 这种 "不区分置信度" 的特性,无法引导 SVM 学习 "大间隔"------ 模型可能仅满足 "分类正确",但间隔极小,泛化能力差。
二、替代损失函数:兼顾 "可优化性" 与 "SVM 目标"
SVM 选择的替代损失函数(如 Hinge 损失、平方 Hinge 损失)需满足两个核心条件:
- 凸性 + 连续性:支持梯度优化,能找到全局最优;
- "铰链式" 惩罚:不仅惩罚错误,还对 "低置信度正确" 的样本施加惩罚,从而引导模型学习大间隔。
以 SVM 中最经典的Hinge 损失(hinge loss,"铰链损失")为例,其定义为:
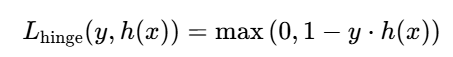
结合定义与图像(y⋅h(x)为 "样本到决策边界的置信度",值越大置信度越高),可清晰看到其优势:
| 样本情况 | y⋅h(x) 范围 | Hinge 损失值 | 物理意义(对 SVM 的作用) |
|---|---|---|---|
| 高置信度正确 | >1 | 0 | 无惩罚,模型无需调整 |
| 低置信度正确 / 临界正确 | (0,1] | (0,1] | 施加惩罚(值越小惩罚越大),倒逼模型增大间隔 |
| 错误 | ≤0 | ≥1 | 施加固定惩罚(至少为 1),强制模型修正错误 |
Hinge 损失与 SVM 的 "完美适配"

三、其他替代损失:为何 Hinge 是 SVM 的首选?
除 Hinge 损失外,二分类中还有平方 Hinge 损失、Logistic 损失等替代方案,但 Hinge 损失更适配 SVM 的原因如下:
| 损失函数 | 定义 | 核心特点 | 与 SVM 的适配性对比 |
|---|---|---|---|
| Hinge 损失 | max(0,1−y⋅h(x)) | 非光滑、对异常值鲁棒(错误样本惩罚上限固定) | ✅ 完美匹配 SVM "最大化间隔" 目标,优化后间隔清晰 |
| 平方 Hinge 损失 | max(0,1−y⋅h(x))2 | 光滑(可导)、对错误样本惩罚更重 | ❌ 对异常值敏感(惩罚随错误程度平方增长),可能缩小间隔 |
| Logistic 损失 | log(1+e−y⋅h(x)) | 光滑、概率可解释(与逻辑回归一致) | ❌ 无 "间隔最大化" 导向,优化后间隔通常小于 Hinge 损失 |
总结:SVM 不用 0/1 损失的核心逻辑
0/1 损失是 "理想但不可用" 的损失函数 ------ 其非凸、非连续 的特性导致无法高效优化,且不区分置信度的设计与 SVM "最大化间隔" 的目标完全冲突。
而 Hinge 等替代损失函数,通过凸性 + 连续性解决了优化难题,通过 **"低置信度惩罚"** 精准匹配了 SVM 的间隔目标,最终成为 SVM 的核心损失函数。这一选择本质是 "任务目标(最大化间隔)" 与 "优化可行性" 权衡后的最优结果。