记一次用Three.js展示360°全景图的折腾

前言

展示360°全景图，最开始我当然是想用自己熟悉的Three.js来实现，Three.js的官方示例中也有全景图的示例，一开始觉得很简单，但真的开发之后发现，Three.js的官方示例在南极和北极有非常明显的形变，像一个菊花一样，这一度让我觉得非常棘手。对此我也看了很多商业厂家提供的全景图功能，发现并没有明显的形变，我意识到肯定是我的实现方式有问题。为了解决这个问题，我折腾了很久，虽然最后发现很简单的方法就能解决这个问题，但我还是决定把这次折腾的过程记录下来，也可以让更多的同学不要掉到我同样的坑里。至于出现问题和最后得以解决的原因，至今我还不能完全想明白，文末我会从我理解的角度尝试分析一下，写这篇文章的目的也是希望有对这方面精通的大神看到了能帮我解答一下疑问。

本文示例的原图是从网上图库中找的一张2:1的全景图，像素是宽10000px，高5000px。为了能在文章中贴出来，我将原图做了压缩，给大家展示下： Three.js官方示例的效果：

可以看到，其它部分效果没什么问题，但是南极的形变还是挺明显的。

官方示例的核心代码：

const textureLoader = new THREE.TextureLoader();
    textureLoader.load('/test2.jpg', texture => {
    texture.colorSpace = THREE.SRGBColorSpace;
    const geometry = new THREE.SphereGeometry( 500, 60, 40 );
    geometry.scale( - 1, 1, 1 );
    const material = new THREE.MeshBasicMaterial( { map: texture } );
    const mesh = new THREE.Mesh( geometry, material );
    scene.add(mesh);
})

折腾过程

Three.js官方示例的实现方式是先用SphereGeometry绘制一个球体几何体，球体的正面向内，然后将全景图作为一个材质贴图贴在球体上。SphereGeometry依照球体经线和纬线的交点生成顶点，绘制球面的三角网格，所以靠近极点的三角网格非常小。而全景图采用‌等距圆柱投影（Equirectangular Projection)，越靠近极点的图像的被横向拉伸越厉害，在将全景图还原到球面时，靠近极点的地方变形比较明显。

最开始我一筹莫展的在网上搜索解决方案，没有找到相关使用Three.js展示全景图并解决这个问题的文章。但是找到了很多其他专门展示全景图的项目，有些项目还是收费的。最后我找到了两个开源项目：Photo-Sphere-Viewer和marzipano。其中Photo-Sphere-Viewer是基于Three.js开发的。

这两个项目我都做了尝试，发现它们的效果在南极确实看不到明显的形变，只是Photo-Sphere-Viewer放大后能看出来一点点马赛克，但也几乎不太影响整体效果。

至此，按理说我的折腾应该到此为止了，得出一个简单的结论：Three.js展示全景图有缺陷，得使用Photo-Sphere-Viewer或marzipano。但是，作为有追求的程序员，还是想探索这背后的原理，为什么Three.js有这个问题，而其他两个项目就没有呢？于是我将这两个项目都下载了下来，决定去源码中寻找答案。

由于Photo-Sphere-Viewer也是基于Three.js的，我决定先看Photo-Sphere-Viewer，我想对比一下，它的实现方法到底有什么高明之处。结果我看了之后发现，Photo-Sphere-Viewer的实现方式和Three.js官方示例中的实现方式几乎一样！也是先绘制一个SphereGeometry球体几何体，然后将全景图作为一个材质贴图贴在球体上。然后我在源码中到处搜索，想找到不同之处，最后我找到了这么几行代码：

texture.minFilter = mimaps ? LinearMipmapLinearFilter : LinearFilter;
texture.generateMipmaps = mimaps;
texture.anisotropy = mimaps ? 2 : 1;

原来，Photo-Sphere-Viewer中texture的minFilter默认是LinearFilter！mipmap默认是不开启的！难道是在纹理缩小过滤时开启了mipmap引起的问题？于是我在Three.js的官方示例中也将minFilter改为了LinearFilter，果然，得出了和Photo-Sphere-Viewer相似的效果。虽然放大看还是能看出一点点马赛克，但是几乎不太影响整体效果。

至此，折腾应该结束了吧？不，毕竟不是还有点马赛克嘛，marzipano的效果并没有，所以marzipano肯定是使用了完全不同的实现方法。于是我开始阅读marzipano的源码。果然，marzipano的实现方式确实不一样，它的方法可以看做是将屏幕空间的点的坐标反投影回世界空间。它先设置一个正方形的平面几何体，正方形的四个顶点分别是，(-1.0, -1.0, 0.0),(1.0, -1.0, 0.0),(1.0, 1.0, 0.0),(-1.0, 1.0, 0.0)，然后这四个顶点坐标传入顶点着色器后，转换成一个四维向量，这个四维向量的x和y分量就是顶点的x和y分量，z和w分量都为1，这四个四维向量就对应裁剪空间中一个平面上的四个边界点，也是屏幕空间的四个边界点，给这四个边界点乘上(视图矩阵×投影矩阵)的逆矩阵，就将裁剪空间中的四个点变换回了世界空间中，然后传入片元着色器，这样屏幕上每个片元都求出了一个对应的世界坐标，然后可以将世界坐标转为球面上对应的球面坐标------极角θ和方位角φ，球面坐标又可以转为全景图上的uv值，这样就可以给每个片元在全景图上采样了。 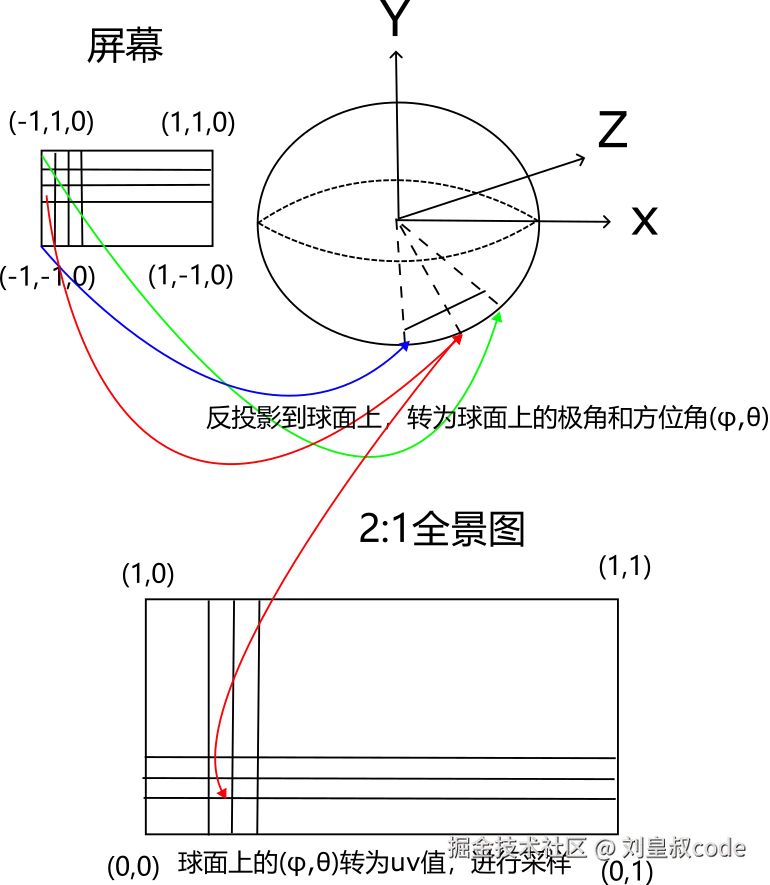下面是marzipano渲染2:1全景图的着色器源码：

顶点着色器：

module.exports = [
'attribute vec3 aVertexPosition;',

'uniform float uDepth;',
'uniform mat4 uViewportMatrix;',
'uniform mat4 uInvProjMatrix;',

'varying vec4 vRay;',

'void main(void) {',
'  vRay = uInvProjMatrix * vec4(aVertexPosition.xy, 1.0, 1.0);',
'  gl_Position = uViewportMatrix * vec4(aVertexPosition.xy, uDepth, 1.0);',
'}'
].join('\n');

片元着色器：

module.exports = [
'#ifdef GL_FRAGMENT_PRECISION_HIGH',
'precision highp float;',
'#else',
'precision mediump float',
'#endif',

'uniform sampler2D uSampler;',
'uniform float uOpacity;',
'uniform float uTextureX;',
'uniform float uTextureY;',
'uniform float uTextureWidth;',
'uniform float uTextureHeight;',
'uniform vec4 uColorOffset;',
'uniform mat4 uColorMatrix;',

'varying vec4 vRay;',

'const float PI = 3.14159265358979323846264;',

'void main(void) {',
'  float r = inversesqrt(vRay.x * vRay.x + vRay.y * vRay.y + vRay.z * vRay.z);',
'  float phi  = acos(vRay.y * r);',
'  float theta = atan(vRay.x, -1.0*vRay.z);',
'  float s = 0.5 + 0.5 * theta / PI;',
'  float t = 1.0 - phi / PI;',

'  s = s * uTextureWidth + uTextureX;',
'  t = t * uTextureHeight + uTextureY;',

'  vec4 color = texture2D(uSampler, vec2(s, t)) * uColorMatrix + uColorOffset;',
'  gl_FragColor = vec4(color.rgba * uOpacity);',
'}'
].join('\n');

在Three.js用反投影实现全景图

知道了原理，我们就可以将marzipano的核心代码"抄"到Three.js中，在Three.js中用这种方法实现全景图的展示，在Three.js中我们用BufferGeometry构造正方形，在ShaderMaterial中写反投影纹理采样的着色器代码，全部代码如下：

import { useEffect, useRef } from "react"
import * as THREE from 'three';

let camera
let scene
let renderer
let requestId

let onPointerDownMouseX = 0, onPointerDownMouseY = 0,
  lon = 0, onPointerDownLon = 0,
  lat = 0, onPointerDownLat = 0,
  phi = 0, theta = 0;

function ThreeContainer() {
  const threeContainer = useRef(null);

  useEffect(() => {
    if (threeContainer.current) {
      scene = new THREE.Scene();
      camera = new THREE.PerspectiveCamera(75, threeContainer.current.clientWidth / threeContainer.current.clientHeight, 1, 1100);
      renderer = new THREE.WebGLRenderer({ antialias: true });
      renderer.setSize(threeContainer.current.clientWidth, threeContainer.current.clientHeight);
      renderer.setPixelRatio(window.devicePixelRatio);
      threeContainer.current.appendChild(renderer.domElement);

      threeContainer.current.addEventListener('pointerdown', onPointerDown);

      document.addEventListener('wheel', onDocumentMouseWheel);
      const textureLoader = new THREE.TextureLoader();
      textureLoader.load('/test2.jpg', texture => {
        texture.colorSpace = THREE.SRGBColorSpace;
        texture.minFilter = THREE.LinearFilter;
        const material = new THREE.ShaderMaterial({
          vertexShader: `
            varying vec4 vRay;
            void main(){
            mat4 invertedMatrix = inverse(projectionMatrix*modelViewMatrix);
            vRay=invertedMatrix*vec4(position.x,position.y,1.,1.);
            gl_Position=vec4(position,1.);
          }`,
          fragmentShader: `
            float PI = 3.14159265358979323846264;
            uniform sampler2D panoMap;
            varying vec4 vRay;
            void main(){
                float r = inversesqrt(vRay.x * vRay.x + vRay.y * vRay.y + vRay.z * vRay.z);
                float phi  = acos(vRay.y * r);
                float theta = atan(vRay.x, -1.0*vRay.z);
                float s = 0.5 + 0.5 * theta / PI;
                float t = 1.0 - phi / PI;
                vec4 testColor = texture2D( panoMap, vec2(s, t) );
                gl_FragColor=testColor;
                #include <colorspace_fragment>
             }`,
          uniforms: {
            panoMap: { value: null }
          }
        });
        material.uniforms.panoMap.value = texture;

        const geometry = new THREE.BufferGeometry();
        const indices = [0, 1, 2, 0, 2, 3]
        const vertices = [-1.0, -1.0, 0.0, 1.0, -1.0, 0.0, 1.0, 1.0, 0.0, -1.0, 1.0, 0.0]
        geometry.setIndex(indices);
        geometry.setAttribute('position', new THREE.Float32BufferAttribute(vertices, 3));

        const mesh = new THREE.Mesh( geometry, material );

        scene.add(mesh);
      })
      requestId = requestAnimationFrame(animate);
    }
    return () => {
      destroyRenderer()
    };
  }, [])

  function onPointerDown(event) {

    if (event.isPrimary === false) return;

    onPointerDownMouseX = event.clientX;
    onPointerDownMouseY = event.clientY;

    onPointerDownLon = lon;
    onPointerDownLat = lat;

    document.addEventListener('pointermove', onPointerMove);
    document.addEventListener('pointerup', onPointerUp);

  }

  function onPointerMove(event) {

    if (event.isPrimary === false) return;

    lon = (onPointerDownMouseX - event.clientX) * 0.1 + onPointerDownLon;
    lat = (event.clientY - onPointerDownMouseY) * 0.1 + onPointerDownLat;

  }

  function onPointerUp(event) {

    if (event.isPrimary === false) return;

    document.removeEventListener('pointermove', onPointerMove);
    document.removeEventListener('pointerup', onPointerUp);

  }

  function onDocumentMouseWheel(event) {

    const fov = camera.fov + event.deltaY * 0.05;

    camera.fov = THREE.MathUtils.clamp(fov, 10, 75);

    camera.updateProjectionMatrix();

  }

  function destroyRenderer() {
    if (requestId) {
      window.cancelAnimationFrame(requestId)
    }
    if (scene) {
      scene.traverse(obj => {
        if (obj instanceof THREE.Mesh) {
          if (obj.isMesh) {
            obj.geometry?.dispose();
            if (Array.isArray(obj.material)) {
              obj.material.forEach(m => disposeMaterial(m));
            } else {
              disposeMaterial(obj.material);
            }
          }
        }
      });
    }

    if (renderer) {
      renderer.domElement.remove();
      renderer.dispose();
      renderer.forceContextLoss();
      renderer = null
    }
  }
  function disposeMaterial(material) {
    material.dispose();
    Object.keys(material).forEach(key => {
      const val = material[key];
      if (val && val instanceof THREE.Texture) {
        // 类型断言后安全调用 dispose 方法
        val.dispose();
      }
    });
  }
  function animate() {
    lat = Math.max(- 85, Math.min(85, lat));
    phi = THREE.MathUtils.degToRad(90 - lat);
    theta = THREE.MathUtils.degToRad(lon);

    const x = 500 * Math.sin(phi) * Math.cos(theta);
    const y = 500 * Math.cos(phi);
    const z = 500 * Math.sin(phi) * Math.sin(theta);

    camera.lookAt(x, y, z);

    renderer?.render(scene, camera);
    requestAnimationFrame(animate);
  }

  return (
    <div ref={threeContainer} className="w-[100%] h-[100%]" id="three-container"></div>
  )
}

export default ThreeContainer

最终效果：

和上面官方示例的效果对比来看，可以说问题完全解决了。

原因分析

这一节我们试着来分析一下产生形变的原因以及反投影没有形变的原因。这里不得不说，我掌握的知识和数学工具有限，只能从我能理解的角度粗浅的分析一下，希望如果有大神看到了能帮我批评指正。

2:1的全景图上的每个像素点都对应球面上相同的立体角角度，但是在球面上，不同纬度的单位立体角对应的球面面积显然不同，高纬度靠近极点上单位立体角对应的球面面积非常小。极点附近的片元在全景图纹理上采样时，uv坐标值是线性插值得到的，这样得到的uv坐标在靠近极点时会和实际出现了很大的偏差，所以视觉上就会有明显的不连续。在缩小过滤时使用mipmap非但不能优化这种走样，反而由于mipmap层间又多了一次线性插值，导致变形更加严重了。

而反投影的方法中，每个片元的uv坐标都是先反投影到球面坐标上，再根据球面坐标计算uv坐标值，然后在全景图纹理上采样的。这样得到的uv值和实际是完全一致的。