MATLAB 代码实现了一个基于物理信息神经网络(Physics-Informed Neural Network, PINN)的高阶偏微分方程(梁振动方程)求解器。以下是详细分析:
一、主要功能
main.m 是主程序,负责:
- 设置问题参数(梁长
L、时间T、训练点数量等); - 生成训练数据(PDE 残差点、初始条件点、边界条件点);
- 构建神经网络结构;
- 训练神经网络;
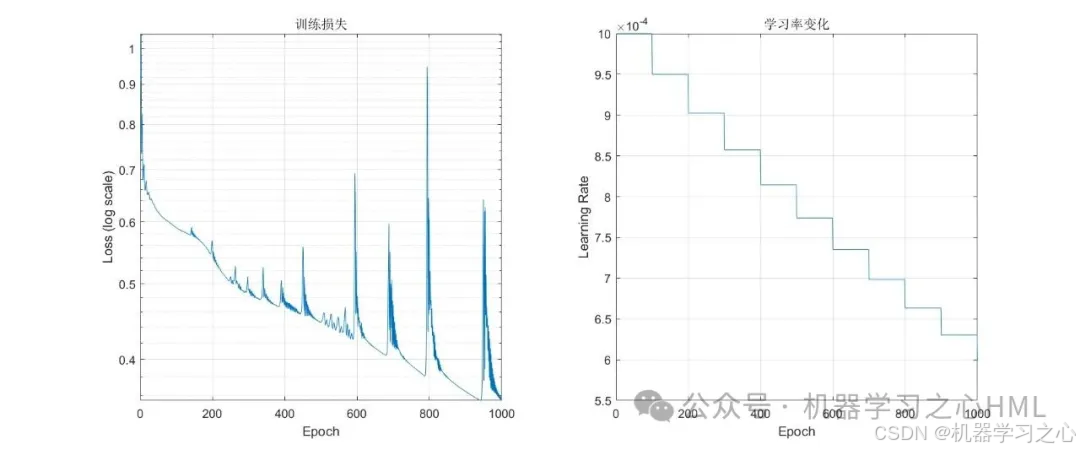
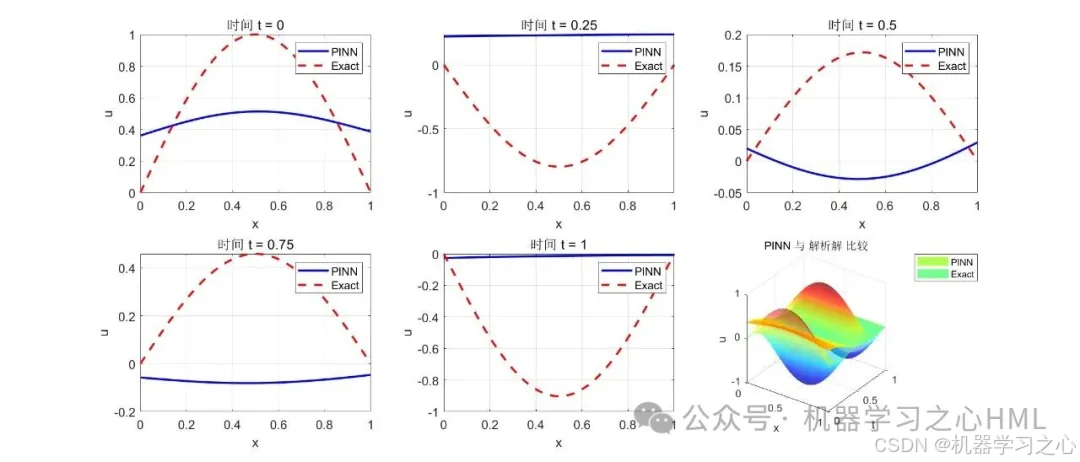
- 预测解并可视化结果(与解析解比较、误差分析)。
modelLoss.m 是自定义损失函数,用于:
- 计算 PDE 残差、初始条件残差、边界条件残差;
- 使用自动微分(
dlgradient)计算高阶导数; - 加权组合各项损失,并返回总损失和梯度。
二、逻辑关联
main.m调用modelLoss.m在训练过程中计算损失和梯度。modelLoss.m中定义的损失函数包含了物理方程(PDE)、初始条件(IC)和边界条件(BC)的约束,确保神经网络学习到物理规律。
三、算法步骤
- 数据生成:在空间和时间域内随机采样点,包括内部点、初始时刻点、边界点。
- 网络构建:使用全连接层 + tanh 激活函数构建深层神经网络。
- 训练循环 :
- 使用 Adam 优化器;
- 动态衰减学习率;
- 每轮计算损失(PDE + IC + BC)并反向传播。
- 预测与评估 :
- 在测试网格上预测解;
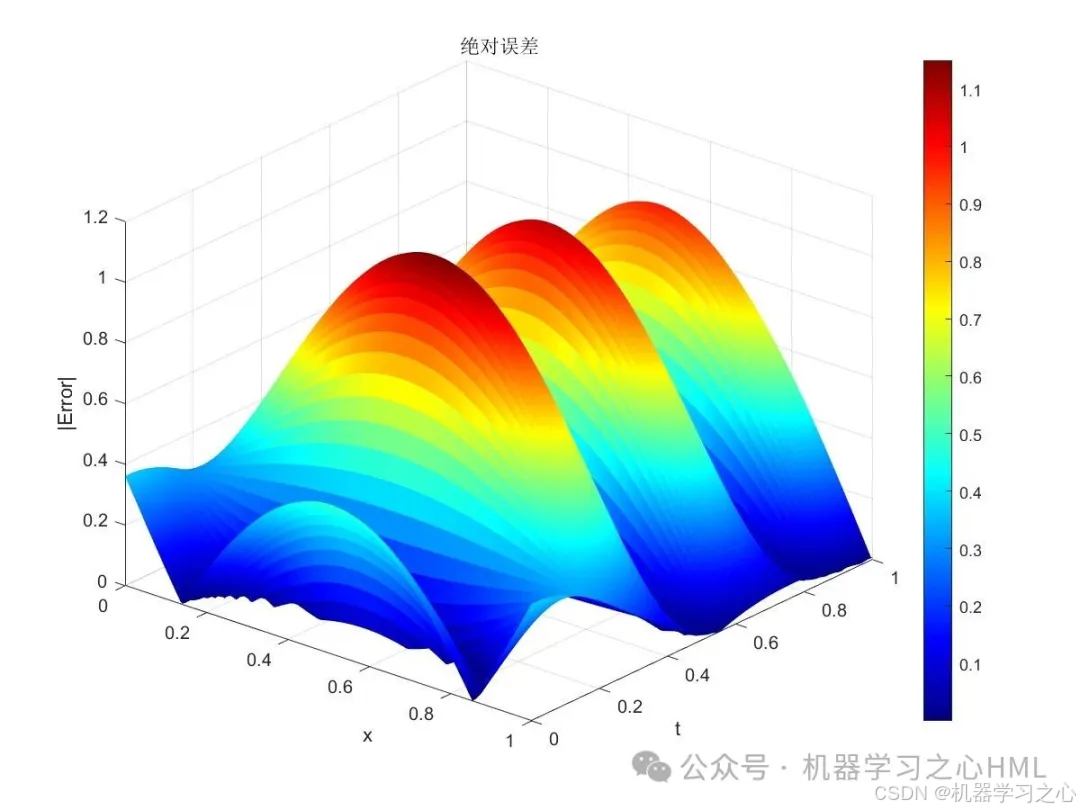
- 与解析解比较,计算误差;
- 可视化结果和训练过程。
四、技术路线
- PINN 方法:将偏微分方程作为正则项嵌入神经网络损失函数中。
- 自动微分 :使用
dlgradient计算高阶导数(如 ( u_{tt} ), ( u_{xxxx} ))。 - 加权多目标损失:为 IC 和 BC 分配更高权重,增强约束。
- 动态学习率衰减:提高训练稳定性。
五、公式原理

六、参数设定
| 参数 | 含义 | 值 |
|---|---|---|
L |
梁长度 | 1 |
T |
时间长度 | 1 |
numPDE |
PDE 残差点数 | 1000 |
numIC |
初始条件点数 | 200 |
numBC |
边界条件点数 | 300 |
numEpochs |
训练轮数 | 1000 |
initialLR |
初始学习率 | 0.001 |
decayRate |
学习率衰减率 | 0.95 |
decaySteps |
衰减步长 | 100 |
七、运行环境
- 软件:MATLAB(需安装 Deep Learning Toolbox)
- 硬件:支持 CPU/GPU 训练(若可用,可加速)
- 版本 :建议 R2021a 或更高版本(因使用
dlarray和dlnetwork)
总结
该代码使用 PINN 方法求解梁振动方程,通过将物理约束嵌入神经网络训练中,避免了传统数值方法对网格的依赖,适用于复杂边界/初始条件的问题。代码结构清晰,包含完整的训练、预测和可视化流程,适合作为 PINN 入门和实践案例。