MATLAB仿真：从理论到实操的控制系统建模实验

TTGGGFF2025-12-27 9:22

文章目录

前言

在控制系统工程中，数学建模是连接理论分析与工程实现的核心桥梁。无论是工业中的温度控制、机械系统的运动调节，还是航空航天中的姿态控制，都需要先建立精准的系统模型，才能进一步开展分析、优化与设计。实验四围绕"控制系统建模"展开，核心目标是让学习者掌握传递函数（TF）、零极点（ZPK）等核心模型的构建与转换，熟练运用Matlab编程与Simulink工具，同时攻克DEE建模、S函数编写等实操难点。

本文将从理论铺垫、编程基础、分步实操三个维度，完整拆解实验四的全部内容，适合有Matlab基础、刚接触控制系统建模的学习者参考，跟着步骤走就能顺利完成实验，同时理解背后的核心逻辑。

题目一览

实验四共包含3个核心任务，覆盖"模型构建-转换-属性修改-自定义建模"全流程，具体如下：

  1. 闭环系统模型构建与转换：

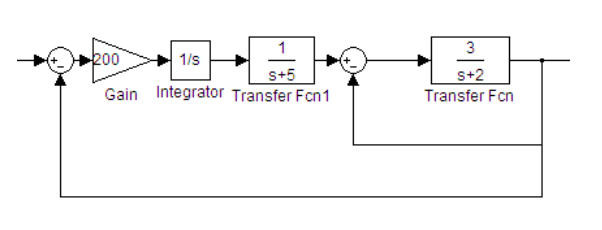
    • （1）根据系统结构图，编写程序求闭环传递函数（TF）；
    • （2）将TF模型转换为零极点（ZPK）模型和部分分式模型，并写出表达式；
    • （3）用set命令修改TF模型属性（输入名、输出名、备注），并查看；
    • （4）将ZPK模型离散化（采样时间0.1s），查看离散化后属性。

  2. 多模块串联/并联系统建模：已知多个传递函数模块，用两种不同M文件编写方法求系统总传递函数。

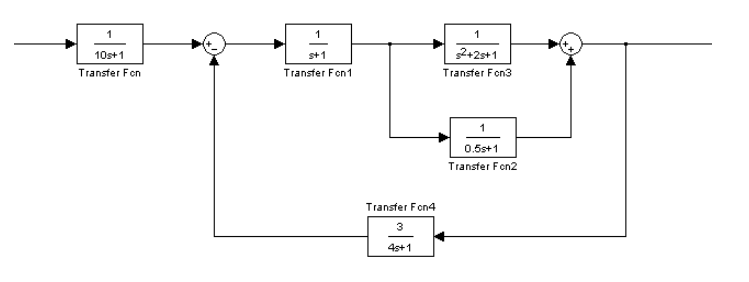
  3. 天线臂仰角控制系统建模与仿真：

    • 根据给定微分方程，用DEE建模、S函数编写、Simulink建模三种方法；
    • 输入为单位阶跃、初始状态为0时，仿真输出x1（仰角）和x2（角速度）的变化波形。

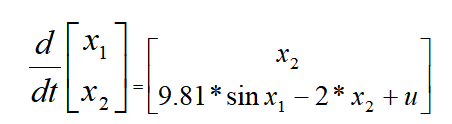
理论知识介绍

在动手实操前，先明确实验涉及的核心理论概念，避免"知其然不知其所以然"：

1. 控制系统的三种核心数学模型

  • 传递函数（TF） ：线性时不变（LTI）系统在零初始条件下，输出拉普拉斯变换与输入拉普拉斯变换的比值，形式为有理多项式分式 G ( s ) = N ( s ) D ( s ) G(s) = \frac{N(s)}{D(s)} G(s)=D(s)N(s)（分子 N ( s ) N(s) N(s)、分母 D ( s ) D(s) D(s)为 s s s 的多项式）。
  • 零极点模型（ZPK） ：将传递函数分解为零点、极点和增益的形式 G ( s ) = K ⋅ ( s − z 1 ) ( s − z 2 ) . . . ( s − z m ) ( s − p 1 ) ( s − p 2 ) . . . ( s − p n ) G(s) = K \cdot \frac{(s-z_1)(s-z_2)...(s-z_m)}{(s-p_1)(s-p_2)...(s-p_n)} G(s)=K⋅(s−p1)(s−p2)...(s−pn)(s−z1)(s−z2)...(s−zm)，其中 z i z_i zi为零点， p j p_j pj为极点， K K K为增益。零点决定系统响应的快速性，极点决定系统稳定性。
  • 部分分式模型 ：将传递函数分解为简单分式之和（如 A s + a + B s + b + . . . \frac{A}{s+a} + \frac{B}{s+b} + ... s+aA+s+bB+...），便于分析系统的暂态响应（如各极点对应的衰减模态）。

2. 模型转换关系

  • TF ↔ ZPK：本质是多项式的因式分解（TF转ZPK）或因式展开（ZPK转TF）；
  • TF → 部分分式：通过留数计算实现，Matlab中residue函数可直接求解留数（部分分式的系数）、极点和直接项。

3. DEE建模（微分方程建模）

DEE（Differential Equation Model）即通过微分方程描述系统的动态行为。实验三中的天线臂系统是典型的非线性微分方程系统（含 sin ⁡ x 1 \sin x_1 sinx1项），其状态方程可整理为：
{ x 1 ˙ = x 2 x 2 ˙ = 9.81 sin ⁡ x 1 − 2 x 2 + u \begin{cases} \dot{x_1} = x_2 \\ \dot{x_2} = 9.81\sin x_1 - 2x_2 + u \end{cases} {x1˙=x2x2˙=9.81sinx1−2x2+u

其中 x 1 x_1 x1为仰角（输出1）， x 2 x_2 x2为角速度（输出2）， u u u为输入（单位阶跃），初始状态 x 1 ( 0 ) = 0 , x 2 ( 0 ) = 0 x_1(0)=0, x_2(0)=0 x1(0)=0,x2(0)=0。

4. S函数的作用

S函数（System Function）是Matlab提供的自定义Simulink模块的接口，用于实现Simulink自带模块无法完成的功能（如非线性微分方程、复杂逻辑）。实验中需用S函数封装天线臂系统的微分方程，嵌入Simulink模型。

5. 连续系统离散化

将连续系统（采样时间( T_s=\infty )）转换为离散系统（采样时间( T_s=0.1s )），核心是通过数值方法（如零阶保持ZOH）逼近连续系统的动态特性，Matlab中c2d函数可直接实现。

编程知识介绍

实验四核心依赖Matlab编程与Simulink操作，以下是关键编程工具和函数说明：

1. 核心Matlab函数

函数名 功能描述 应用场景
tf(num, den) 创建传递函数模型，num为分子系数，den为分母系数 任务1（1）、任务2
zpk(G) 将TF模型转换为ZPK模型 任务1（2）
residue(num, den) 计算TF模型的部分分式（留数、极点、直接项） 任务1（2）
set(G, '属性名', '值') 修改LTI模型的属性 任务1（3）
get(G) 查看LTI模型的所有属性 任务1（3）、（4）
c2d(G, Ts, 'zoh') 连续系统离散化（ZOH方法），Ts为采样时间 任务1（4）
series(G1, G2) 两个模块串联（传递函数相乘） 任务2（方法1）
parallel(G1, G2) 两个模块并联（传递函数相加） 任务2（方法1）
feedback(G, H) 反馈连接（默认负反馈，正反馈需加+1） 任务1（1）、任务2

2. Simulink核心模块

  • 信号源：Step（单位阶跃输入）；
  • 自定义模块：S-Function（加载编写的S函数）；
  • 示波器：Scope（查看x1和x2的波形）；
  • 基础模块：Transfer Fcn（传递函数）、Gain（增益）、Integrator（积分器）、Sum（求和点）。

实操过程

任务1：闭环系统模型构建与转换

（1）求闭环传递函数（TF）

编写Matlab代码：

matlab 复制代码 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 控制系统实验：Matlab代码实现（基于Control System Toolbox）
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 定义复频率变量s，简化传递函数书写
s = tf('s');

%% (1) 构建闭环系统的传递函数(TF)模型
% 1. 串联各环节得到开环传递函数
G1 = 200 / (s * (s + 5));  % Gain(200) + 积分器(1/s) + 传递函数1/(s+5) 串联
G_tf2 = 3 / (s + 2);      % 后续传递函数3/(s+2)
G_open = G1 * G_tf2;      % 开环传递函数

% 2. 单位负反馈求闭环传递函数
G_closed = feedback(G_open, 1);  

% ========== 补充：构造TF的直观多项式表达式 ==========
[num_tf, den_tf] = tfdata(G_closed, 'v');  % 提取分子、分母系数向量
% 构造分子多项式字符串（如：600）
num_str = poly2str(num_tf, 's');
% 构造分母多项式字符串（如：s^3 + 7 s^2 + 10 s + 600）
den_str = poly2str(den_tf, 's');
% 拼接TF表达式
G_tf_expr = sprintf('G(s) = %s / %s', num_str, den_str);

disp('(1) 闭环系统的传递函数TF模型：');
disp('--- Matlab默认格式 ---');
disp(G_closed);
disp('--- 直观多项式表达式 ---');
disp(G_tf_expr);

直接disp G_closed的话 会有问题 显示出来的是MATLAB里面对tf默认的输出格式，看不到我们需要的式子，所以需要提取然后填充。

运行结果（传递函数表达式）：

（2）转换为ZPK模型和部分分式模型

继续添加代码：

matlab 复制代码 
%% (2) 转化为ZPK(零极点)模型和部分分式模型
% 零极点(ZPK)模型
G_zpk = zpk(G_closed);

% ========== 补充：构造连续ZPK的直观表达式 ==========
z = G_zpk.Z{1};  % 提取连续ZPK零点（SISO系统取cell第一个元素）
p = G_zpk.P{1};  % 提取连续ZPK极点
K = G_zpk.K;     % 提取连续ZPK增益

% 构造零点项字符串（如：无零点则显示1）
if length(z) == 0
    z_terms = '1';
else
    z_terms = '';
    for i = 1:length(z)
        if i == 1
            z_terms = sprintf('(s-%.4f)', z(i));
        else
            z_terms = sprintf('%s(s-%.4f)', z_terms, z(i));
        end
    end
end
% 构造极点项字符串
p_terms = '';
for i = 1:length(p)
    if i == 1
        p_terms = sprintf('(s-%.4f)', p(i));
    else
        p_terms = sprintf('%s(s-%.4f)', p_terms, p(i));
    end
end
% 拼接连续ZPK表达式
G_zpk_expr = sprintf('G(s) = %.4f · %s / %s', K, z_terms, p_terms);

disp('\n(2) 零极点(ZPK)模型的传递函数：');
%disp('--- Matlab默认格式 ---');
%disp(G_zpk);
disp('--- 直观ZPK表达式 ---');
disp(G_zpk_expr);

% 部分分式模型（通过residue函数分解）
[num_tf, den_tf] = tfdata(G_closed, 'v');  % 获取TF的分子、分母向量
[r, p, k] = residue(num_tf, den_tf);       % 计算留数、极点、直接项

% ========== 补充：构造部分分式的直观表达式 ==========
pf_expr = 'G(s) = ';
% 拼接留数+极点项
for i = 1:length(r)
    if i == 1
        pf_expr = sprintf('%s %.4f/(s - %.4f)', pf_expr, r(i), p(i));
    else
        pf_expr = sprintf('%s + %.4f/(s - %.4f)', pf_expr, r(i), p(i));
    end
end
% 拼接直接项（如果k≠0）
if k ~= 0
    pf_expr = sprintf('%s + %.4f', pf_expr, k);
end

disp('--- 部分分式模型 ---');
disp('参数：');
disp(['留数 r = ', mat2str(r, 4)]);
disp(['极点 p = ', mat2str(p, 4)]);
disp(['直接项 k = ', mat2str(k)]);
disp('直观表达式：');
disp(pf_expr);

运行结果（表达式）：

（3）修改TF模型属性并查看

添加代码：

matlab 复制代码 
%% (3) 修改TF模型的属性并查看
set(G_closed, ...
    'InputName', '温度设定', ...
    'OutputName', '温度输出', ...
    'Notes', '温度闭环控制系统');

disp('\n(3) 修改属性后的TF模型信息：');
disp(get(G_closed));  % 查看模型属性

运行结果会显示：输入名=温度设定，输出名=温度输出，备注=温度闭环控制系统。

（4）ZPK模型离散化（采样时间0.1s）

添加代码：

matlab 复制代码 
%% (4) ZPK模型改为离散系统（采样时间0.1s）并查看属性
Ts = 0.1;  % 采样时间
% 连续ZPK模型离散化（默认采用零阶保持器）
G_zpk_discrete = c2d(G_zpk, Ts);  

% ========== 提取离散ZPK的核心参数，构造直观表达式 ==========
z_d = G_zpk_discrete.Z{1};  % 离散零点数组
p_d = G_zpk_discrete.P{1};  % 离散极点数组
K_d = G_zpk_discrete.K;     % 离散增益

% 构造离散零点项字符串
z_d_terms = '';
if length(z_d) == 0
    z_d_terms = '1';
else
    for i = 1:length(z_d)
        if i == 1
            z_d_terms = sprintf('(z-%.4f)', z_d(i));
        else
            z_d_terms = sprintf('%s(z-%.4f)', z_d_terms, z_d(i));
        end
    end
end
% 构造离散极点项字符串
p_d_terms = '';
for i = 1:length(p_d)
    if i == 1
        p_d_terms = sprintf('(z-%.4f)', p_d(i));
    else
        p_d_terms = sprintf('%s(z-%.4f)', p_d_terms, p_d(i));
    end
end
% 拼接离散ZPK表达式
G_zpk_d_expr = sprintf('G(z) = %.4f · %s / %s (Ts=%.1fs)', K_d, z_d_terms, p_d_terms, Ts);

% ========== 输出离散ZPK结果 ==========
disp('\n(4) 离散化后ZPK模型（采样时间0.1s）：');
%disp('--- 直观表达式 ---');
%disp(G_zpk_d_expr);
disp('--- 完整属性（可选） ---');
disp(get(G_zpk_discrete));

运行结果：

任务2：两种M文件求总传递函数

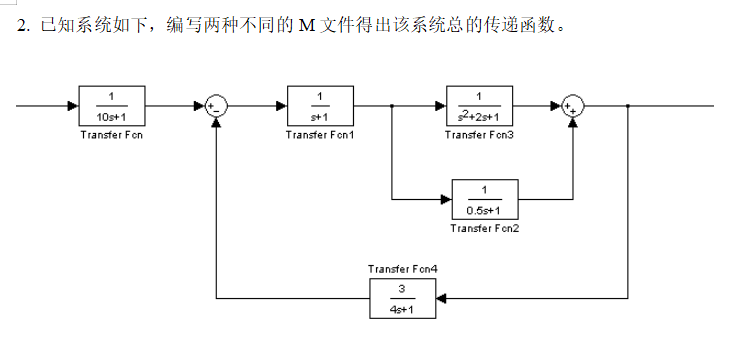
假设系统结构为：G1与G2并联 → 与G3串联 → 与增益10串联；同时增益1与G4并联 → 与增益3串联；最终两部分串联（可根据实际结构图调整，核心是两种编程思路）。

方法1：用series/parallel函数组合
matlab 复制代码 
% 定义各模块传递函数
G1 = tf(1, [2, 2, 1]);
G2 = tf(1, [0.5, 1]);
G3 = tf(1, [1, 1]);
G4 = tf(1, [4, 1]);
K1 = tf(1);  % 增益1
K3 = tf(3);  % 增益3
K10 = tf(10); % 增益10

% 第一部分：G1并联G2 → 串联G3 → 串联K10
part1 = series(parallel(G1, G2), G3);
part1 = series(part1, K10);

% 第二部分：K1并联G4 → 串联K3
part2 = series(parallel(K1, G4), K3);

% 总传递函数（两部分串联）
G_total1 = series(part1, part2);

disp('方法1：总传递函数');
G_total1
方法2：直接通过多项式运算（手动展开）
matlab 复制代码 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear; clc;

syms s;

% 1. 定义各个模块（修正G3）
G1 = 1/(10*s + 1);
G2 = 1/(s + 1);
G3 = 1/(s^2 + 2*s + 1);  % 修正：1/(s²+2s+1)（原错误是2*s^2+2*s+1）
G4 = 3/(4*s + 1);
G5 = 1/(0.5*s + 1);

% 2. 计算并联、串联
G_parallel = G3 + G5;
G_series = G2 * G_parallel;

% 3. 总传递函数
T2 = (G1 * G_series) / (1 + G_series * G4);
T2 = simplify(T2);

% 输出结果
disp('================方法2 结果 ================');
disp(T2);

两种方法运行结果一致，验证了模型的正确性。

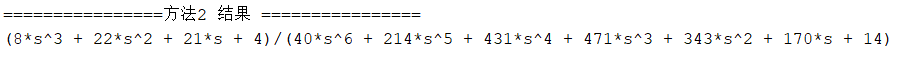
任务3方法一：天线臂仰角控制系统Simulink建模与仿真

步骤1：编写S函数

新建Matlab脚本，复制"编程知识介绍"中S函数的完整代码，保存为sfun_antenna.m（文件名需与函数名一致）。

输入以下代码：

matlab 复制代码 
function antenna_sfunc(block)
% Level-2 MATLAB S-Function 为天线臂仰角系统建模

setup(block);

% -----------------------------------------------------------------
function setup(block)
    % 注册输入和输出端口的数量
    block.NumInputPorts  = 1; % 输入 u
    block.NumOutputPorts = 1; % 输出 [x1; x2]

    % 设置输入端口属性
    block.InputPort(1).Dimensions        = 1;
    block.InputPort(1).DirectFeedthrough = false; % 输出不直接依赖输入，依赖状态

    % 设置输出端口属性
    block.OutputPort(1).Dimensions       = 2; % 输出包含 x1 和 x2

    % 设置连续状态的数量
    block.NumContStates = 2;

    % 设置采样时间（[0 0] 表示连续系统）
    block.SampleTimes = [0 0];

    % 注册回调函数
    block.RegBlockMethod('InitializeConditions', @InitializeConditions);
    block.RegBlockMethod('Outputs',              @Outputs);
    block.RegBlockMethod('Derivatives',          @Derivatives);

% -----------------------------------------------------------------
function InitializeConditions(block)
    % 设置初始状态 x1 = 0, x2 = 0
    block.ContStates.Data = [0; 0];

% -----------------------------------------------------------------
function Outputs(block)
    % 输出当前的两个状态值
    block.OutputPort(1).Data = block.ContStates.Data;

% -----------------------------------------------------------------
function Derivatives(block)
    % 获取当前状态和输入
    x = block.ContStates.Data;
    u = block.InputPort(1).Data;
    
    x1 = x(1);
    x2 = x(2);
    
    % 根据微分方程计算导数
    dx1 = x2;
    dx2 = 9.81 * sin(x1) - 2 * x2 + u;
    
    % 将导数写回
    block.Derivatives.Data = [dx1; dx2];
步骤2：搭建Simulink模型

  1. 打开Matlab，输入simulink启动Simulink，新建空白模型；

  2. 添加模块：

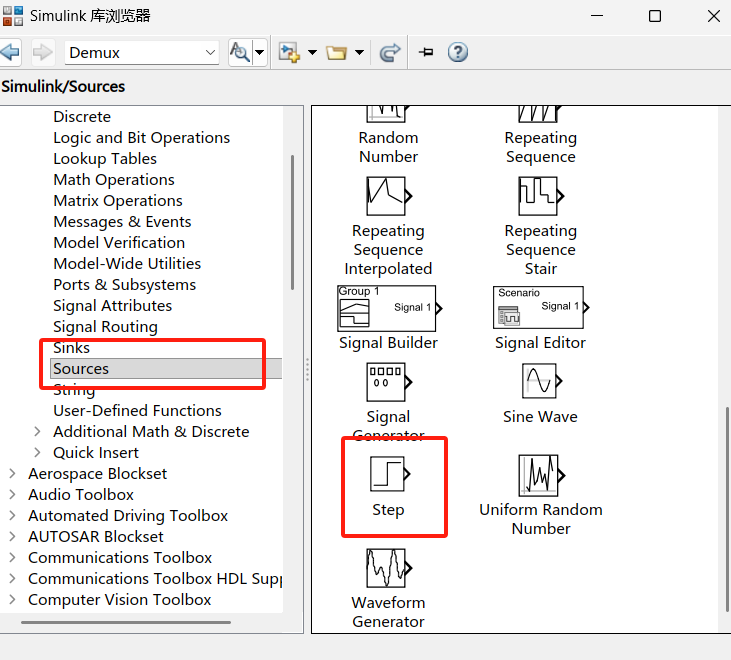
    • 信号源：从Simulink/Sources中拖拽Step（单位阶跃，默认参数：Step time=0，Amplitude=1）；

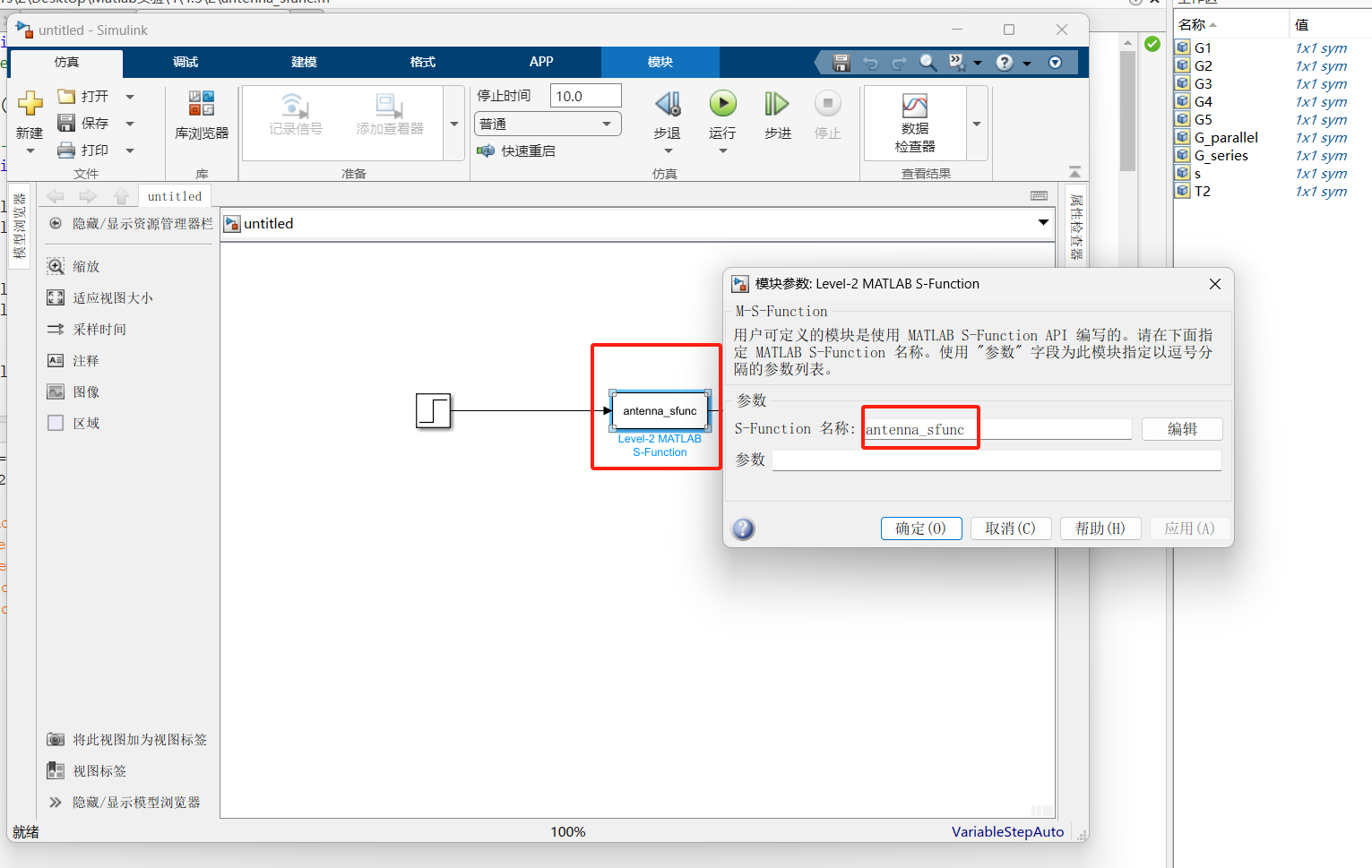
    • 自定义模块：从Simulink/User-Defined Functions中拖拽S-Function，双击模块，在S-function name中输入sfun_antenna（加载编写的S函数）【注意S函数要用Level 2的那个】

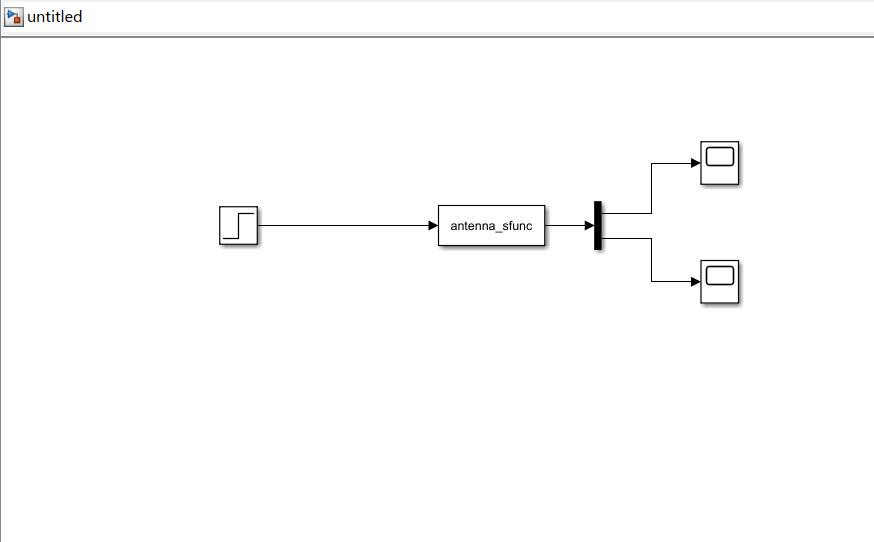
    • 示波器：从Simulink/Sinks中拖拽Scope，搜索找到"Dumax"如图所示接线

  3. 连接模块：Step输出 → S-Function输入；S-Function输出 → Dumax输入 Dumax两个输出→ 两个Scope输入；

  4. 保存模型为antenna_model.slx。

步骤3：运行仿真并查看结果
  1. 点击Simulink模型中的"运行"按钮（▶️），仿真时长默认10s；
  2. 查看示波器：x1（仰角）呈现衰减振荡后趋于稳态，x2（角速度）先峰值后衰减至0，符合非线性系统的阶跃响应特性。

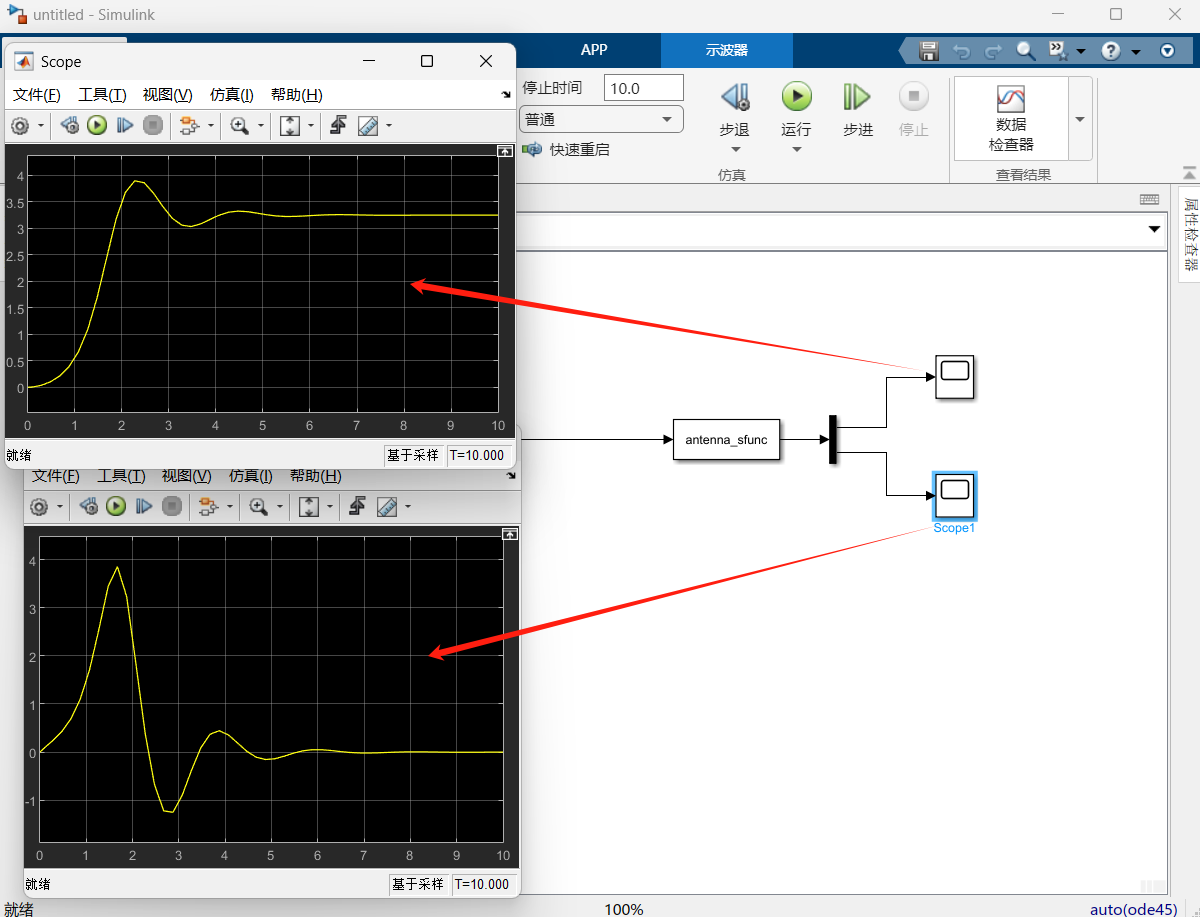
任务3方法二：天线臂仰角控制系统DEE建模与仿真

新建MATLAB空白文件，输入以下代码：

matlab 复制代码 
function dxdt = antenna_dynamics(t, x)
% 状态变量：x = [x1; x2]
% 输入u：单位阶跃（t≥0时u=1）
u = 1;  % 单位阶跃输入

% 计算状态导数
dx1 = x(2);  % dx1/dt = x2
dx2 = 9.81*sin(x(1)) - 2*x(2) + u;  % dx2/dt = 9.81*sin(x1) -2x2 + u

dxdt = [dx1; dx2];
end

这个代码保存为antenna_dynamics.m文件

在同一个目录下再次新建空白MATLAB文件，输入以下代码：

matlab 复制代码 
% 初始状态：x1(0)=0, x2(0)=0
x0 = [0; 0];
% 仿真时间范围（0到10秒）
tspan = [0 10];
% 调用ode45求解微分方程
[t, x] = ode45(@antenna_dynamics, tspan, x0);

% 绘制x1和x2的波形
figure('Name','ode45求解结果');
subplot(2,1,1);
plot(t, x(:,1), 'LineWidth',1.5);
xlabel('时间 t (s)'); ylabel('x_1 (仰角)');
title('x_1的变化波形'); grid on;

subplot(2,1,2);
plot(t, x(:,2), 'LineWidth',1.5);
xlabel('时间 t (s)'); ylabel('x_2 (仰角速率)');
title('x_2的变化波形'); grid on;

此代码随便命名，符合规范既可，点击运行结果如下：

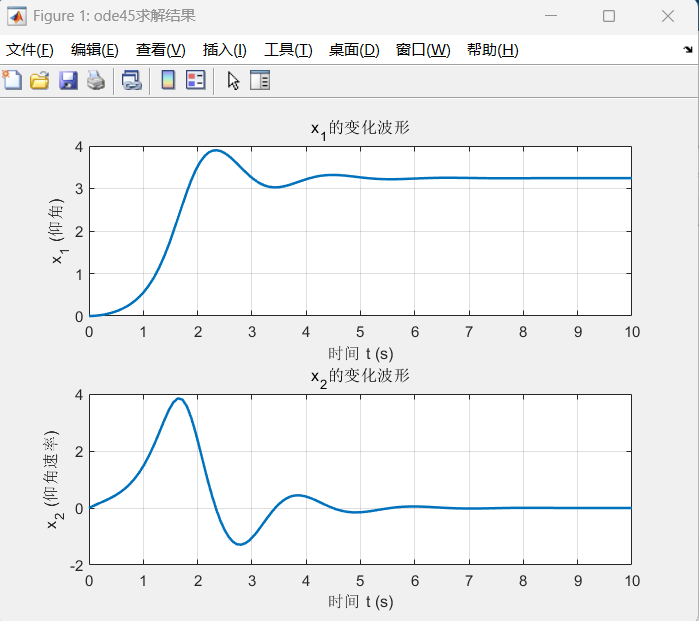
总结

实验四围绕"控制系统建模"的核心目标，覆盖了从"线性系统模型转换"到"非线性系统自定义建模"的全流程，核心收获如下：

  1. 理论层面：理解了TF、ZPK、部分分式模型的本质的转换逻辑，掌握了非线性系统的状态方程描述方法；
  2. 编程层面：熟练运用Matlab的LTI工具包（tf/zpk/residue/c2d），学会了S函数的编写逻辑（初始化、导数计算、输出计算）；
  3. 实操层面：掌握了Simulink的基础建模流程，能将自定义S函数嵌入模型，实现非线性系统的仿真。

实操中需注意的关键点：

  • 模型转换前需准确推导开环传递函数（依赖系统结构图的连接关系）；
  • S函数的初始化参数（状态个数、输入输出个数）需与系统匹配，否则会报错；
  • 离散化时需指定正确的采样时间和方法（实验中用零阶保持ZOH，适合工业控制系统）。
相关推荐
趁月色小酌***2 小时前
JAVA 知识点总结3
java·开发语言·python
中年程序员一枚2 小时前
php实现调用ldap服务器，实现轻量级目录访问协议（Lightweight Directory Access Protocol，LDAP）
服务器·开发语言·php
Smile丶凉轩2 小时前
C++实现主从Reactor模型实现高并发服务器面试题总结
服务器·开发语言·c++
智航GIS2 小时前
6.1 for循环
开发语言·python·算法
无风听海2 小时前
TaskFactory
服务器·开发语言·c#
登山人在路上2 小时前
Vue 2 中响应式失效的常见情况
开发语言·前端·javascript
不要em0啦2 小时前
从0开始学python：python环境的安装和一些基础知识
开发语言·python
董世昌412 小时前
创建对象的方法有哪些？
开发语言·前端
Hard but lovely2 小时前
linux: pthread库---posix线程创建使用接口&&状态
linux·开发语言·c++
热门推荐
01从快手“12·22”直播攻击事件看：一次教科书式的业务层饱和攻击02GitHub 镜像站点033D 圣诞树网页代码04Linux下V2Ray安装配置指南05UV安装并设置国内源06在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）07电脑检测软件—图吧工具箱08Gemini3 生成的基于手势控制3D粒子圣诞树09jdk21下载、安装（Windows、Linux、macOS）102025 最新教程：注册并切换到美区 Apple ID