PINNs分数阶扩散方程的参数反演模型MATLAB代码

一、研究背景

1.1 科学问题

分数阶扩散方程：描述反常扩散现象，比整数阶扩散方程更能准确刻画记忆性、非局域性等复杂扩散过程
参数反演问题：实际应用中扩散系数c和分数阶指数s通常未知，需通过观测数据反演

1.2 技术背景

物理信息神经网络（PINNs）：将物理方程约束融入神经网络损失函数
谱方法：利用Hermite正交基函数高效逼近空间解
数据同化：结合观测数据与物理模型进行参数估计

二、主要功能

2.1 核心功能

数据生成：生成带噪声的分数阶扩散方程观测数据
参数反演：从时间序列数据中反演扩散系数c和分数阶指数s
误差分析：评估反演参数的准确性和稳定性

2.2 辅助功能

可视化反演结果与误差分布
统计反演性能指标

三、算法步骤

3.1 数据准备阶段

复制代码

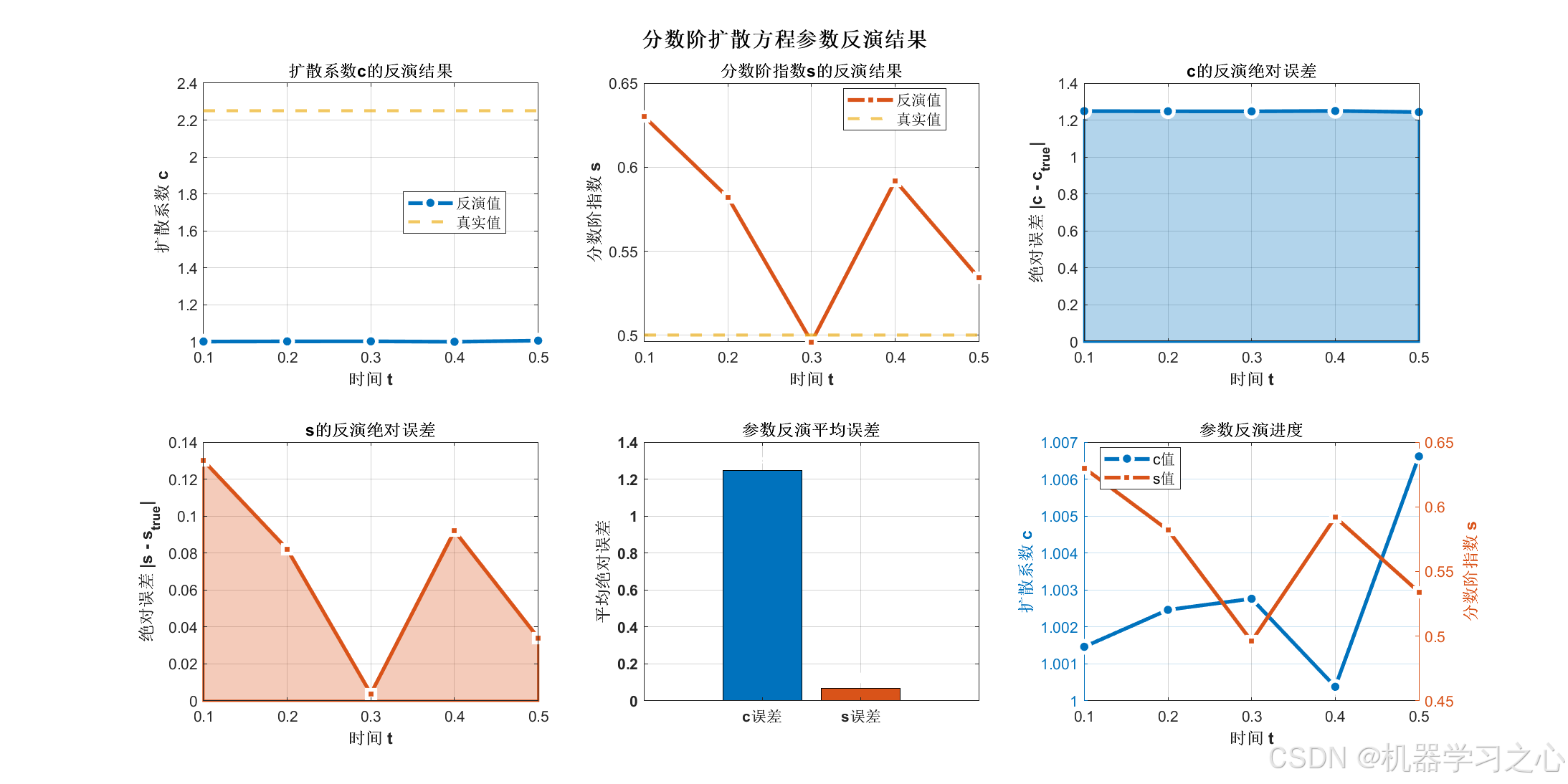
1. 设置真实参数 (c_true, s_true)
2. 生成Gauss-Hermite求积节点和权重
3. 构建精确解并添加噪声生成观测数据

3.2 参数反演阶段

复制代码

4. 对每个时间步 [t_j, t_{j+1}]：
   a. 提取两个连续时间步的观测数据
   b. 构建损失函数（数据拟合 + 时间演化约束）
   c. 使用fmincon优化器求解最小化问题
   d. 记录反演参数及误差

3.3 后处理阶段

复制代码

5. 绘制参数反演结果和误差曲线
6. 计算统计指标并输出结果

四、技术路线

4.1 方法架构

复制代码

观测数据 → 谱方法展开 → 神经网络逼近 → 物理约束优化 → 参数反演

4.2 关键技术

谱方法：使用Hermite正交多项式基函数
matlab 复制代码
```
H(:,n+1) = hermiteH(n, xi);  % 构建Hermite基函数矩阵
```
正则化最小二乘：稳定求解谱系数
matlab 复制代码
```
A_reg = A + lambda * eye(size(A));  % Tikhonov正则化
```
物理约束优化：结合数据拟合与方程残差

五、公式原理

5.1 分数阶扩散方程

复制代码

∂u/∂t = -c * (-Δ)^{s/2} u + f(u) + g(x,t)

其中：

c：扩散系数
s：分数阶指数（0 < s < 1）
f(u)：非线性反应项（此处为三次多项式）
g(x,t)：源项

5.2 谱展开形式

解在Hermite基函数下展开：

复制代码

u(x,t) ≈ Σ_{n=0}^{Nx} a_n(t) H_n(x)

5.3 损失函数

复制代码

J(c,s) = ||u_obs - u_recon||² + α||u_pred - u_obs||²

其中第二项为简化时间演化约束。

六、参数设定

6.1 物理参数

matlab 复制代码

c_true = 2.25;     % 扩散系数真实值
s_true = 0.5;      % 分数阶指数真实值
T = 0.5;           % 总时间
dt = 0.1;          % 时间步长

6.2 数值参数

matlab 复制代码

Nx = 4;            % Hermite多项式截断阶数
sigma_list = [0];  % 噪声水平（0表示无噪声）

6.3 神经网络参数

matlab 复制代码

layers = [          % 简单全连接网络
    featureInputLayer(1)
    fullyConnectedLayer(20)
    reluLayer()
    fullyConnectedLayer(20)
    reluLayer()
    fullyConnectedLayer(Nx+1)  % 输出谱系数
]

6.4 优化参数

matlab 复制代码

x0 = [2.0, 0.4];   % 初始猜测 [c, s]
lb = [1.0, 0.1];   % 下界约束
ub = [3.0, 0.9];   % 上界约束

七、运行环境

7.1 软件环境

MATLAB版本：R2018b或更高版本
必需工具箱 ：
- Deep Learning Toolbox（神经网络）
- Optimization Toolbox（fmincon优化器）
- Statistics and Machine Learning Toolbox（随机数生成）

7.2 硬件要求

内存：≥ 4GB
处理器：支持AVX指令集的Intel/AMD CPU

7.3 依赖函数

matlab 复制代码

% 核心自定义函数：
custom_hermite_gauss()     % Gauss-Hermite求积节点生成
hermite_spectral_stable()  % 稳定的谱系数计算
simplified_loss()          % 损失函数计算
compute_rhs()             % 方程右端项计算
compute_g_simple()        % 简化源项计算

八、应用场景

8.1 科学研究

反常扩散建模：多孔介质、生物组织、金融市场中的非正常扩散
参数识别：从实验数据中识别物理参数

8.2 工程应用

地下水流：含水层参数反演
热传导：复合材料热扩散系数估计
污染物传输：环境工程中的扩散参数识别

8.3 教学演示

PINNs方法教学示例
参数反演算法验证
谱方法应用案例

九、代码特点与局限性

9.1 优点

结构清晰：模块化设计，易于理解和修改
计算高效：简化模型快速验证算法有效性
可视化完整：提供全面的结果分析和可视化

9.2 局限性

简化假设：分数阶导数用整数阶近似，精度有限
小规模测试：Nx=4截断阶数较低，分辨率有限
噪声处理简单：仅考虑高斯加性噪声
时间离散简化：显式欧拉格式，稳定性限制大