一、集成学习核心原理
1.1 基本定义
集成学习（Ensemble Learning）通过组合多个弱学习器（Weak Learner）构建强学习器，其泛化误差可表示为：
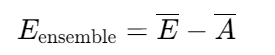
其中：
- E：各弱学习器误差的加权平均
- A：学习器间的多样性度量（正相关性越小，泛化能力越强）
1.2 两大范式对比
| 特性 | Bagging | Boosting |
|---|---|---|
| 样本权重 | 均匀分布 | 动态调整（关注错分样本） |
| 训练方式 | 并行 | 串行 |
| 方差-偏差 | 主要降低方差 | 主要降低偏差 |
| 代表性算法 | 随机森林 | Adaboost/GBDT/XGBoost |
二、Bagging与随机森林数学详解（600字）
2.1 Bootstrap抽样数学本质
设数据集 D 含 N 个样本，有放回抽样生成子集 Dt：
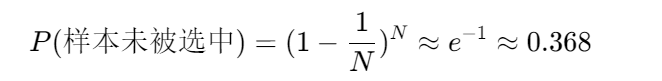
即每个子集约含63.2%的原始样本，剩余36.8%形成袋外数据（OOB）。
2.2 随机森林双随机性
-
特征随机 ：分裂时从 M 个特征随机选 m（通常
） -
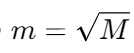决策树构建 ：节点分裂依据基尼不纯度最小化：
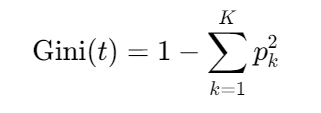
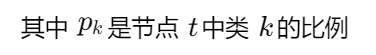
三、Boosting算法数学推导
3.1 Adaboost核心公式
权重更新机制：
-
初始权重：
-
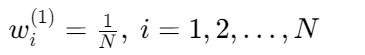
第 t 轮弱学习器错误率：
-
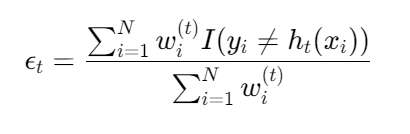
学习器权重：
-
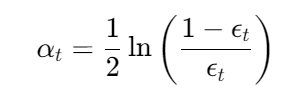
样本权重更新：
-
规范化：
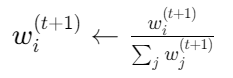
3.2 GBDT梯度提升原理
伪残差计算 ：
对于损失函数 L，第 t 轮伪残差：
ri,t=−[∂F(xi)∂L(yi,F(xi))]F(x)=Ft−1(x)
- 平方损失：ri,t=yi−Ft−1(xi)（残差）
- 绝对损失：ri,t=sign(yi−Ft−1(xi))
- 对数损失：ri,t=yi−1+e−Ft−1(xi)1
模型更新 ：
Ft(x)=Ft−1(x)+ν∑i=1Nri,t⋅I(x∈Rj,t)
其中：
- ν：学习率（shrinkage系数）
- Rj,t：第 t 轮树的叶子区域
3.3 XGBoost二阶泰勒展开
目标函数分解 ：
其中正则项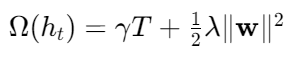 
二阶泰勒近似 ：
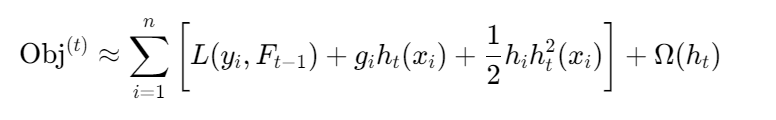
其中：
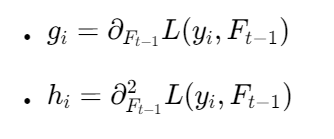
叶子权重解析解 ：
定义叶子 j 的实例集合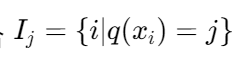
，则最优权重：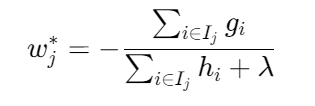
结构分数（增益公式） ：
该公式指导特征选择与分裂点决策
四 、关键对比总结
| 维度 | Bagging（如随机森林） | Boosting（如Adaboost/GBDT） |
|---|---|---|
| 数据使用 | 独立有放回抽样 | 全数据集，权重调整 |
| 模型关系 | 并行独立训练 | 串行依赖训练 |
| 过拟合风险 | 低（双重随机性） | 需控制学习率和树复杂度 |
| 代表算法 | 随机森林 | Adaboost, GBDT, XGBoost |
五 、实践案例要点
泰坦尼克号预测：
特征工程：处理缺失值（Age填充均值）、类别编码（Sex的One-hot）。
随机森林 vs 决策树：RF显著提升准确率（约5-10%）。
红酒品质分类：
多分类问题：XGBoost需设objective='multi:softmax'。
样本不均衡：使用class_weight='balanced'调整权重。
六 、高频考点解析
Q：为什么随机森林要随机抽样和随机选特征？
A：打破弱学习器间的相关性，提升泛化能力（若所有树用相同数据/特征，投票结果相同）。
Q：GBDT拟合的是残差还是负梯度？
A：负梯度（残差是平方损失下的特例）。
Q：XGBoost如何防止过拟合？
A ：正则化项（
gamma控制分裂阈值，lambda约束叶子权重）+ 学习率eta缩减。