PID算法
普通PID(Proportional-Integral-Derivative)
通过比例(P)、积分(I)和微分(D)三项来进行控制
-
比例项(P):根据当前误差(目标值与实际值之差)进行控制。误差越大,控制量也越大,但容易导致稳态误差。
P = K p ⋅ e ( t ) P = K_p \cdot e(t) P=Kp⋅e(t)
-
积分项(I):累积误差,可以消除稳态误差,特别是在误差长时间存在时,但可能会导致系统超调和震荡。
I = K i ⋅ ∫ e ( t ) d t I = K_i \cdot \int e(t) \, dt I=Ki⋅∫e(t)dt
-
微分项(D):根据误差的变化率进行控制,用来预测误差的变化,从而减小超调和改善系统响应速度。
D = K d ⋅ d d t e ( t ) D = K_d \cdot \frac{d}{dt} e(t) D=Kd⋅dtde(t)
PID的实现分为两种:
- 标准型PID: D = K ( e ( t ) + 1 τ i ∫ e ( t ) + 1 τ d d e ( t ) d t ) D = K(e(t)+ \frac{1}{\tau_i} \int e(t)+ \frac{1}{\tau_d} \frac{de(t)}{dt}) D=K(e(t)+τi1∫e(t)+τd1dtde(t))
- τ i \tau_i τi称为积分时间,物理含义为积分项需要多长时间才能追上比例项, τ d \tau_d τd称为微分时间,物理含义为比例项需要多久才能追上微分项。
- 并联型PID: D = K p e ( t ) + K i ∫ e ( t ) + K d d e ( t ) d t D = K_pe(t)+ K_i \int e(t)+ K_d \frac{de(t)}{dt} D=Kpe(t)+Ki∫e(t)+Kddtde(t)
标准型PID的好处在于确定了积分时间 τ i \tau_i τi和微分时间 τ d \tau_d τd之后,系统就只剩一个增益参数需要调节了。
将其进行拉普拉斯变换得到频域格式: C = K p ( 1 + 1 T i s + T d s ) C = K_p\left(1 + \frac{1}{T_i s} + T_ds\right) C=Kp(1+Tis1+Tds)
- 在matlab中提供了标准型PID的函数pidstd,但是文档中可以看到其频域公式格式为: C = K p ( 1 + 1 T i s + T d s T d N s + 1 ) C = K_p\left(1 + \frac{1}{T_i s} + \frac{T_d s}{\frac{T_d}{N} s + 1}\right) C=Kp(1+Tis1+NTds+1Tds),这其中的N为滤波器除数。
- 因为实际使用中,信号多来自于传感器,具有一些高频噪声,普通的微分环节从频率响应的角度来看,其幅频特性 ∣ G ( j ω ) ∣ = K d ω |G(j\omega)|=K_d\omega ∣G(jω)∣=Kdω,会放大高频信号,导致系统不稳定。
- 通过在微分环节中添加一个低通滤波器 G ( s ) = 1 1 ω c s + 1 G(s)=\frac{1}{\frac{1}{\omega_c}s+1} G(s)=ωc1s+11,然后整体的传递函数变为 G ( s ) = K d s 1 ω c s + 1 G(s)=\frac{K_ds}{\frac{1}{\omega_c}s+1} G(s)=ωc1s+1Kds,其幅频特性为 ∣ G ( j ω ) ∣ = ∣ K d ( j ω ) 1 ω c ( j ω ) + 1 ∣ = ∣ K d ( j ω ) ∣ ∣ 1 ω c ( j ω ) + 1 ∣ = K d ⋅ ω 1 + ( ω ω c ) 2 |G(j\omega)|=|\frac{K_d (j\omega)}{\frac{1}{\omega_c}(j\omega)+ 1}|=\frac{|K_d (j\omega)|}{|\frac{1}{\omega_c}(j\omega)+ 1|}=\frac{K_d \cdot \omega}{\sqrt{1 + \left( \frac{\omega}{\omega_c} \right)^2}} ∣G(jω)∣=∣ωc1(jω)+1Kd(jω)∣=∣ωc1(jω)+1∣∣Kd(jω)∣=1+(ωcω)2 Kd⋅ω,当 ω \omega ω较小时,跟普通微分环节没什么区别,当 ω \omega ω较大时,幅频特性趋近于常数 K d K_d Kd,避免了高频信号的干扰。
其中, u ( t ) u(t) u(t) 是控制信号, K p K_p Kp, K i K_i Ki, K d K_d Kd 是PID常数, e ( t ) e(t) e(t) 是误差。
适用于简单控制,Simulink中也有封装好的PID模块,用单环PID控制一个直流有刷电机仿真如下:
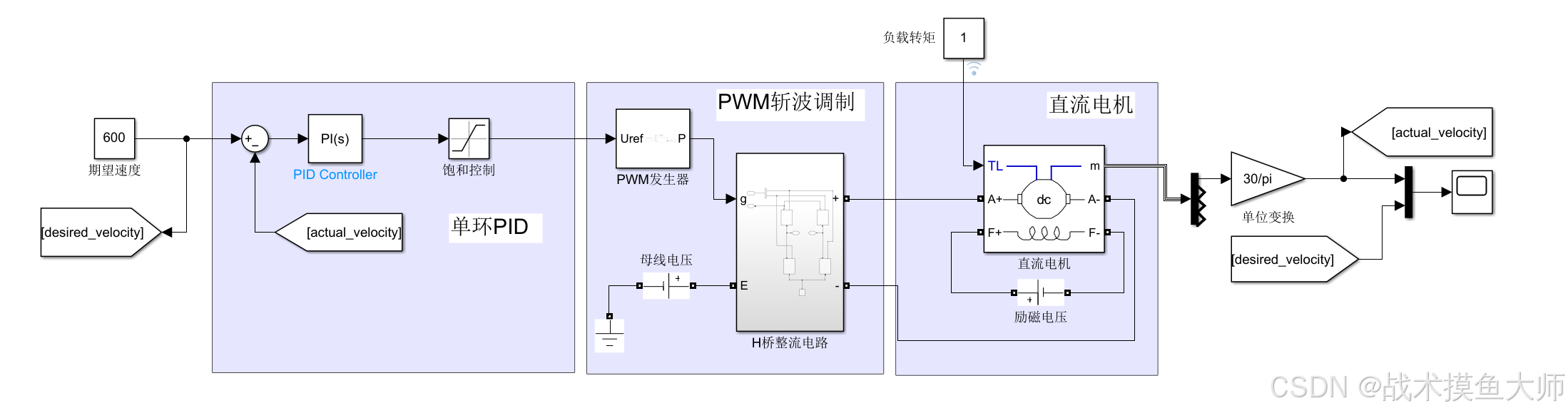
可以尝试一下在电机转速actual_velocity中添加一些低幅值的高频噪声,会发现对于系统的稳定影响非常大。
采用单环PID控制,使用PWM进行斩波调制,将母线电压控制到想要的电压大小,实现的效果如下:
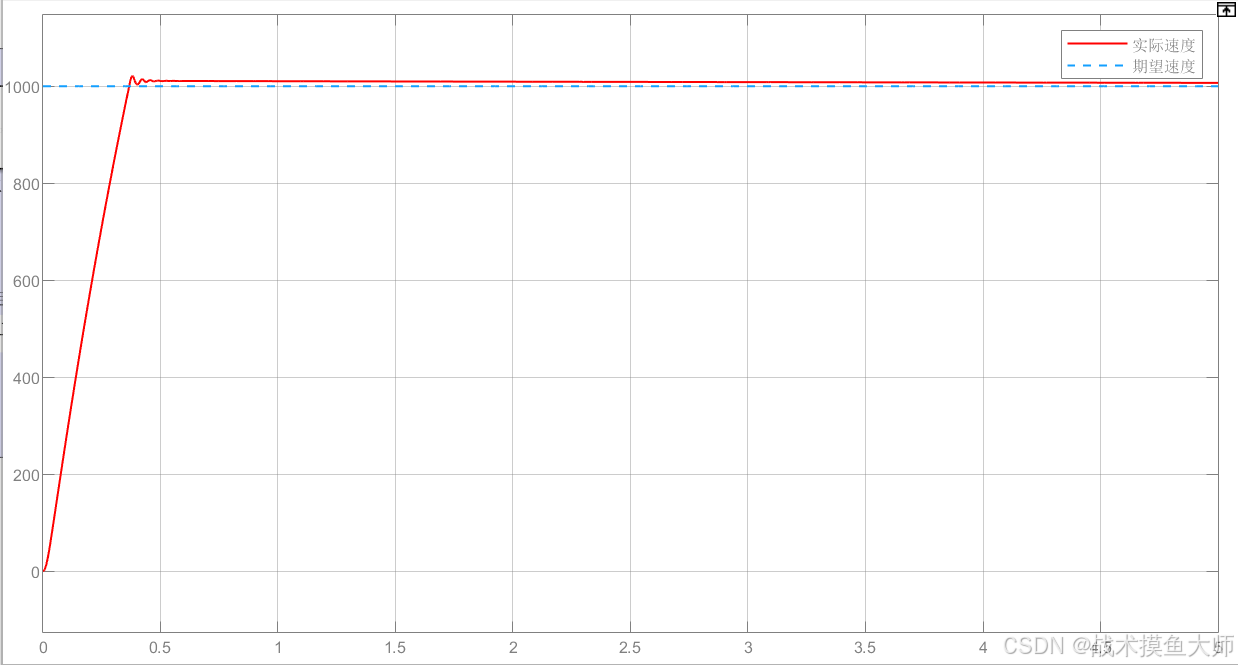
用python实现一个PID用于控制摆锤(约等于电机控制问题)
python
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
import gymnasium as gym
# 解决中文显示问题
def setup_font():
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC", "Arial Unicode MS"]
plt.rcParams['axes.unicode_minus'] = False
setup_font()
class PIDController:
"""连续输出的PID控制器"""
def __init__(self, kp, ki, kd, setpoint=0):
self.kp = kp # 比例增益
self.ki = ki # 积分增益
self.kd = kd # 微分增益
self.setpoint = setpoint # 目标摆角(弧度)
self.prev_error = 0.0 # 上一时刻误差
self.integral = 0.0 # 误差积分
self.dt = 0.05 # 时间步长(与Pendulum环境一致)
def compute(self, process_value):
"""计算连续控制输出(力矩)"""
# 计算当前误差(摆角偏差)
error = self.setpoint - process_value
# 积分项(限制积分饱和)
self.integral += error * self.dt
# 微分项(抑制噪声)
derivative = (error - self.prev_error) / self.dt
self.prev_error = error
# 计算PID输出(连续力矩)
output = self.kp * error + self.ki * self.integral + self.kd * derivative
# 限制输出在环境允许的力矩范围内
return np.clip(output, -2, 2)
def run_simulation(kp=10.0, ki=1.0, kd=2.0, render=True):
"""在Pendulum-v1环境中运行PID控制"""
# 创建连续动作空间的倒立摆环境
env = gym.make('Pendulum-v1', render_mode='human' if render else None, g=3)
# 初始化PID控制器(目标:摆角为0,即垂直向上)
pid = PIDController(kp, ki, kd)
# 存储数据
states = []
actions = []
rewards = []
# 重置环境(初始摆角)
observation, info = env.reset(options={"theta": -3.14})
done = False
# 仿真主循环
while not done:
# 观测值解析:[cos(theta), sin(theta), theta_dot]
# 计算实际摆角(弧度)
cos_theta, sin_theta, theta_dot = observation
theta = np.arctan2(sin_theta, cos_theta) # 转换为[-π, π]的摆角
# PID计算连续力矩(动作)
torque = pid.compute(theta)
action = np.array([torque]) # 环境要求动作是数组形式
# 执行动作
next_observation, reward, terminated, truncated, info = env.step(action)
done = terminated or truncated
# 存储数据
states.append([theta, theta_dot]) # 保存摆角和角速度
actions.append(torque)
rewards.append(reward)
observation = next_observation
env.close()
# 转换为数组
states = np.array(states)
actions = np.array(actions)
rewards = np.array(rewards)
return states, actions, rewards
def plot_results(states, actions, rewards):
"""绘制控制结果"""
time_steps = len(states)
dt = 0.05 # 时间步长
time = np.arange(time_steps) * dt
fig, axs = plt.subplots(3, 1, figsize=(10, 12))
# 摆角(转换为度)
axs[0].plot(time, np.rad2deg(states[:, 0]), label='实际摆角')
axs[0].axhline(y=0, color='r', linestyle='--', label='目标摆角')
axs[0].set_title('摆角变化(度)')
axs[0].set_ylabel('角度')
axs[0].grid(True)
axs[0].legend()
# 摆角速度(转换为度/秒)
axs[1].plot(time, np.rad2deg(states[:, 1]), label='摆角速度')
axs[1].set_title('摆角速度变化(度/秒)')
axs[1].set_ylabel('角速度')
axs[1].grid(True)
axs[1].legend()
# 控制力矩
axs[2].plot(time, actions, label='输出力矩')
axs[2].set_title('PID输出力矩变化')
axs[2].set_xlabel('时间(秒)')
axs[2].set_ylabel('力矩')
axs[2].grid(True)
axs[2].legend()
plt.tight_layout()
plt.show()
if __name__ == "__main__":
# 调优后的PID参数(连续动作空间下)
kp = 14.0 # 比例增益:主导纠正摆角偏差
ki = 0.9 # 积分增益:消除稳态误差
kd = 3.0 # 微分增益:抑制震荡
# 运行仿真
states, actions, rewards = run_simulation(kp=kp, ki=ki, kd=kd, render=True)
print(f"仿真持续时间: {len(states)*0.05:.2f}秒")
print(f"最终摆角: {np.rad2deg(states[-1, 0]):.2f}度")
# 绘制结果
plot_results(states, actions, rewards)仿真结果如下:
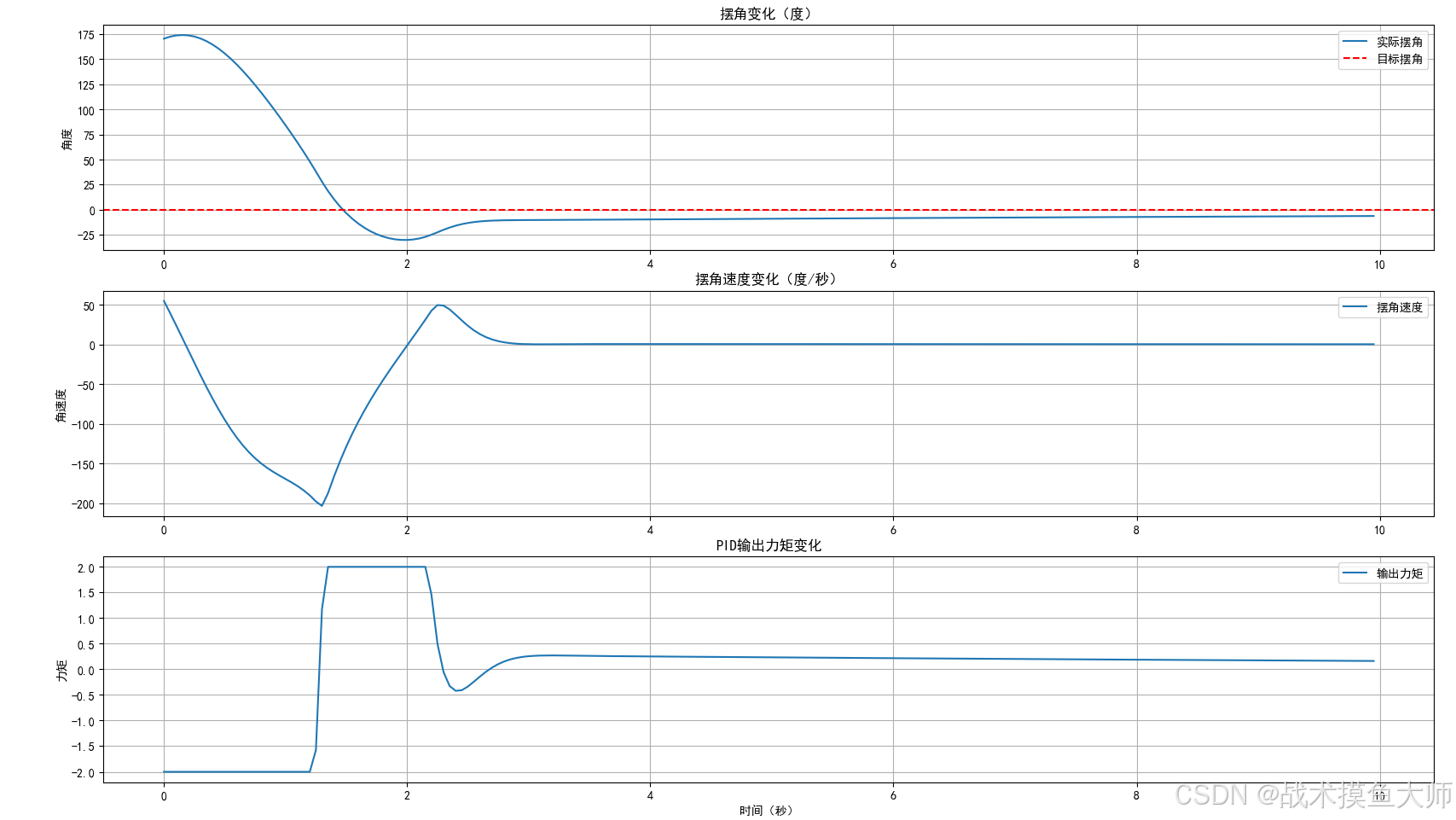
仿真系统可以设置重力常数g,进而影响力矩,当g较大时,这个单环PID控制器就失效了,因为PID是误差驱动,在最低端时角度会从-180跳变到180,即在最低点左边PID会驱动摆锤向左转,反之亦然。这就导致PID无法做到像运动员助跑一样,在最低点左边向右加速助力从右边转上去,直观的体现就是PID一直在左右摇摆就是上不去。
还有之前使用强化学习方法做的样例,可以参考:
强化学习DDPG算法Demo实现
级联PID(Cascade PID)
级联PID控制算法是对普通PID的扩展,通常用于多变量控制系统。它的核心思想是将一个主控制器和一个或多个子控制器结合起来,使得系统能更好地处理复杂的动态行为。
在级联PID中,主控制器负责控制整个系统的大范围误差,而子控制器则负责细化处理主控制器的控制输出。这种结构适用于需要分层控制的场景,例如温度控制、压力控制等。
- 主回路:根据主回路的误差计算出一个控制量,通常是设定值和实际值之间的差。
- 子回路:主回路的控制输出作为子回路的设定值。子回路的作用是进一步精细调整,控制精度通常较高。
这种方法的优点是可以减少滞后效应,快速响应动态变化,提高系统的稳定性。
在电机控制中,可以使用级联PID进行控制:
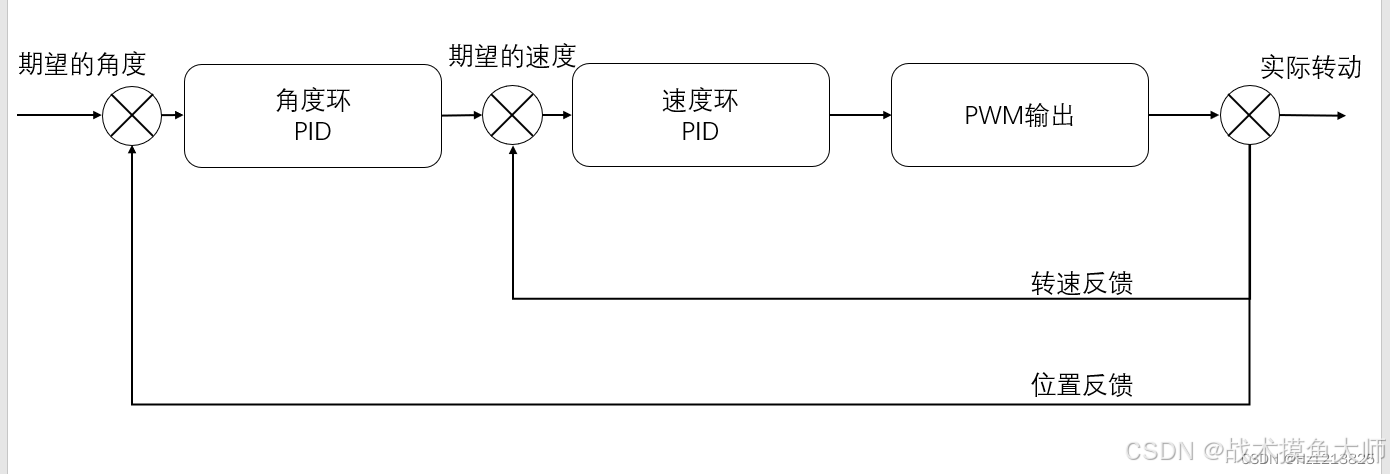
使用速度环和电流环的电机控制如下:
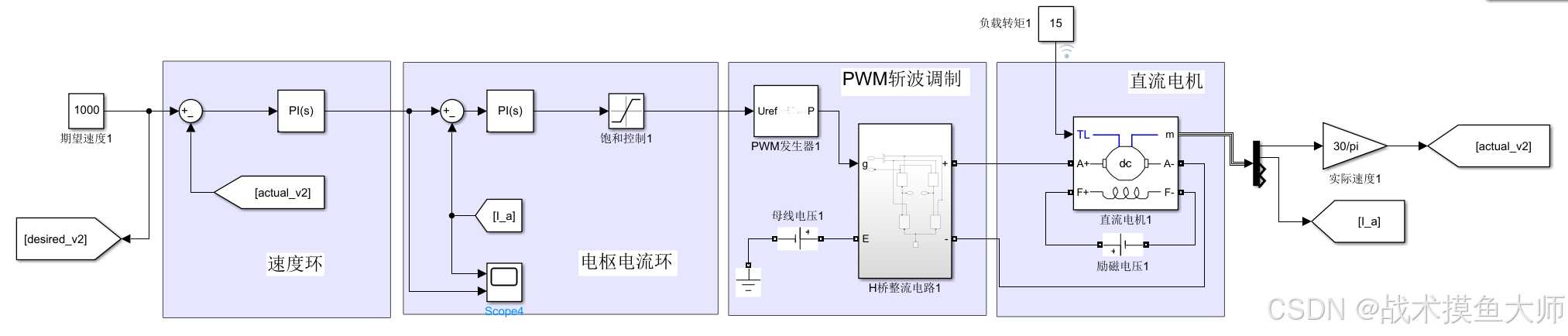
得到的效果如下:
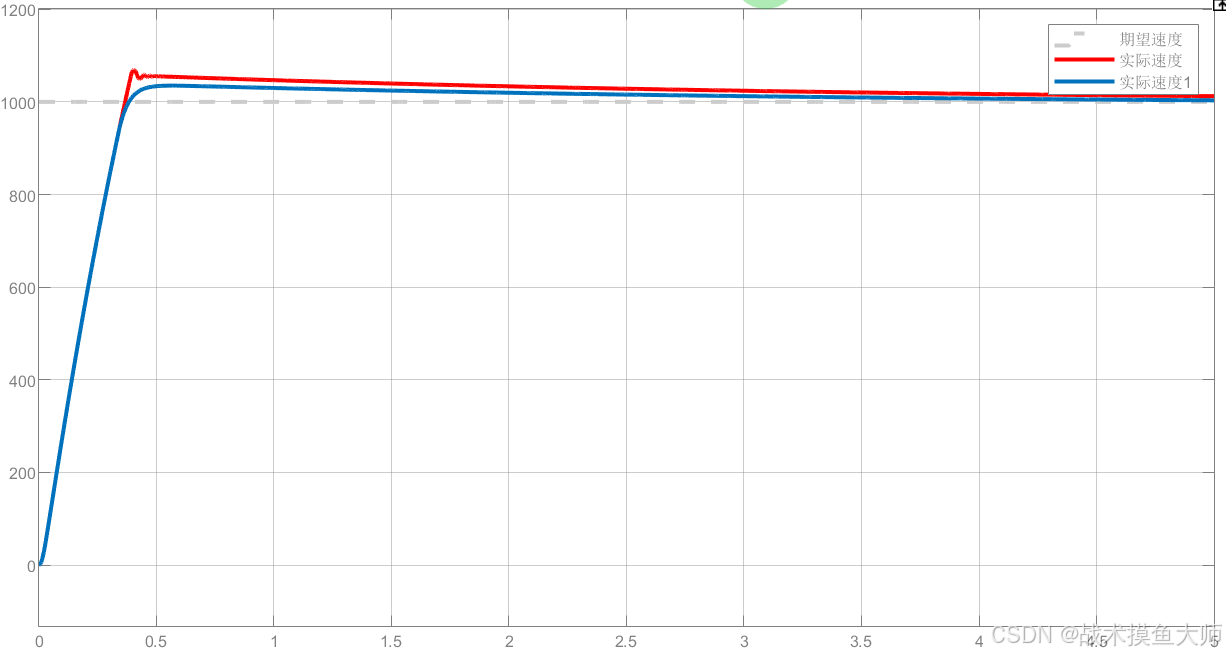
参数整定
PID控制器是自动控制系统中非常常见的一种反馈控制器。它通过比例(P)、积分(I)和微分(D)三个参数来调节系统的输出,以达到设定值。PID参数整定的目的是确定这三个参数的最佳值,以使控制系统在性能上达到最佳。
经验调试
经验整定法是最简单的一种方法,通常用于经验丰富的工程师通过反复调整PID控制器的参数(Kp、Ki、Kd)来达到满意的控制效果。
- 过程 :
- 先设置
Ki和Kd为零。 - 调整
Kp,直到系统出现小的稳态误差,并使系统不产生大的超调量。 - 调整
Ki以消除稳态误差。 - 最后,调整
Kd以减少系统的振荡或过冲。
- 先设置
- 优缺点 :
- 优点:简单直观,适用于对系统了解较多的场合。
- 缺点:操作繁琐,且需要根据经验来调整参数,可能导致不稳定或效率不高。
PID调参口诀:
参数整定找最佳,从小到大顺序查;
先是比例后积分,最后再把微分加;
曲线振荡很频繁,比例度盘要放大;
曲线漂浮绕大弯,比例度盘往小扳;
曲线偏离回复慢,积分时间往下降;
曲线波动周期长,积分时间再加长;
理想曲线两个波,前高后低4比1;
一看二调多分析,调节质量不会低。
PID参数的整定方法主要包括: 基于响应法、模型解析法、 设计图谱法、目标优化法等。其中,基于响应法包括经典的Ziegler-Nichols整定法和继电器反馈法,通过实测系统的时域响应曲线,辨识系统的临界特征参数,进而调节PID参数。常见的PID参数整定方法有以下几种:
Ziegler-Nichols方法
Ziegler-Nichols法是基于响应的经典整定方法,适用于大多数控制系统。它通过设置不同的控制器参数,观察系统响应,进而获得PID参数。
-
步骤:
-
设置
Ki和Kd为零,仅调整Kp(比例增益),直到系统发生持续振荡(临界振荡)。 -
记录此时的
Kp值(临界增益Kc)和振荡周期Pc。 -
根据Ziegler-Nichols表格,通过
Kc和Pc计算出PID参数:- P控制 :
Kp = 0.5 * Kc - PI控制 :
Kp = 0.45 * Kc, Ki = 1.2 * Kp / Pc - PID控制 :
Kp = 0.6 * Kc, Ki = 2 * Kp / Pc, Kd = Kp * Pc / 8
- P控制 :
-
-
优缺点:
- 优点:简单有效,能够快速获得较为合理的控制参数。
- 缺点:对系统的初始调节有较高要求,且可能存在一定的超调和震荡。
优化算法法
这种方法通过优化算法来自动搜索PID控制器的最佳参数。常用的优化算法包括:
- 遗传算法:通过模拟自然选择的过程,逐步寻找最佳PID参数。
- 粒子群优化算法(PSO):通过模拟粒子在搜索空间中的运动来寻求最优解。
- 最小二乘法:通过最小化误差平方和来优化PID参数。
优缺点:
- 优点:适用于复杂的控制系统,能够自动找到最佳的PID参数。
- 缺点:计算量大,且依赖于算法的选择和参数设置。
频域分析法
在频域中,通过对系统的传递函数进行分析,可以在系统频率响应上调节PID参数。频域整定法通常依赖于系统的开环增益和相位特性。
- 步骤 :
- 通过频率响应法(例如伯德图)分析系统的幅频特性。
- 根据系统的相位裕度和增益裕度来确定PID的参数。
- 优缺点 :
- 优点:对于大部分线性系统适用,能够精确调节系统的动态性能。
- 缺点:需要较强的系统建模和频域分析能力。
总结
PID参数整定的选择应依据具体系统的特点、对性能的要求以及对控制过程的理解来决定。一般情况下,Ziegler-Nichols方法是最常用的整定方法,但对于更为复杂或精密的系统,可能需要采用优化算法或其他方法来精细调整。