参考视频:【MATLAB机器人工具箱10.4 机械臂仿真教学(未完结)】 https://www.bilibili.com/video/BV1q44y1x7WC/?p=6\&share_source=copy_web\&vd_source=2c56c6a2645587b49d62e5b12b253dca
写在前面:
插值算法在《机器人学导论》(约翰J克雷格著)第145页,如果没看过也没关系,下面我们会一起快速复习一遍。
本节内容很丰富,逻辑连贯一脉相承,需要2-3小时的理解和实操时间,极其不建议在课间或上课阅读,不被打断的思路很重要。
下面是本节的逻辑链,看不懂也没关系,等看完之后我们还会一起过一遍。
首先我们明确了轨迹规划的任务,包括了空间规划 和时间规划 ,使用的方法是插值法 ;
接着我们复习了书上最简单的关节空间的三项式插值 ,理解了最基本的原理。
接着我们一起学习了时间上是如何控制的,linspace 负责控制开始结束和插值点数,
lspb、tpoly 负责将其映射到坐标上,完成时间上的插值;
然后我们学习了一个通用的插值方式------mtraj ,他负责多维的插值控制,可以选择@空间映射函数。
接着我们学习了笛卡尔空间的空间规划器------trinterp和ctraj 。
最后我们发现,当仿真涉及姿态的变换时,前面这些方法都行不通,这是因为笛卡尔空间的连续性经过逆解后无法推得关节空间的连续性 ,也就是逆解对连续没有传递性。
因此我们想出来用jtraj 直接在关节空间插值,彻底解决了这个难题。
轨迹规划复习速通
轨迹规划就是给定时间 和初末位姿 ,计算过程中的轨迹、速度、加速度,以给下位机控制。
轨迹规划包括两个维度的规划------时间和空间,首先要进行空间的规划,从理综楼到食堂如何走?
接着规划下楼走得快走得慢,大路走得快走得慢,食堂上楼走得快走得慢。
轨迹规划的两大核心:空间 vs 时间
目标:让机械臂末端从位姿 P1 平滑移动到 P2
这需要三个步骤:
| 步骤 | 任务 | 所需函数 |
|---|---|---|
| 1️⃣ 空间路径规划 | 定义"怎么走":从 P1 到 P2 的空间路径 | ctraj 或 trinterp |
| 2️⃣ 时间节奏控制 | 定义"走多快":慢启动 → 快 → 慢停止 | tpoly / lspb / linspace |
| 3️⃣ 逆运动学求解 + 可视化 | 把空间轨迹转成关节角,驱动机器人 | ikine / plot |
一般空间规划 我们通过封装的函数实现(ctraj、trinterp、mtraj、jtraj),重点讨论的是时间上如何规划。
下面举一个最简单的规划方式------三项式插值
因为时间是影响加速度,也就是力的最重要因素,设想:
假设是直线插值,那么在初末状态的速度加速度就是无限大,是不可能实现的,因此考虑将速度轨迹弯曲一些,使得导数(加速度)小一些。
于是有了三项式插值,但是这样初末的加速度还是有可能超过硬件限制,因此增加最高次项,使得速度轨迹、加速度轨迹更加平滑。
至于为什么是奇数次插值,是因为我们解决多项式插值的时候使用参数对应的方式求解,一个x次多项式有x+1个系数,通过初末状态的约束解出系数,而约束是初末的位置、速度、加速度,他们是成对出现的,因此插值都是奇数次插值。
下面是在关节空间内进行的三次多项式插值,如果是在笛卡尔空间中,直接把θ替换为x即可。
比如对于三次多项式,约束条件就是:
1.初始时刻关节变量θ(0)=θ0 终点时刻关节变量θ(t)=θt
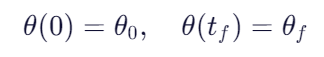
2.初末速度连续
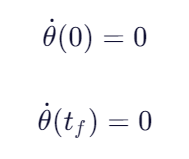
3.(五次多项式要求加速度也连续)
那么由三次多项式插值公式就能得到:
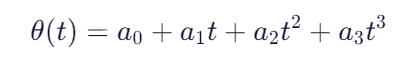
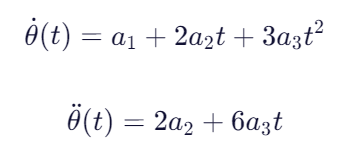
接下来要通过这个式子和前面设定的四条约束解出参数a。
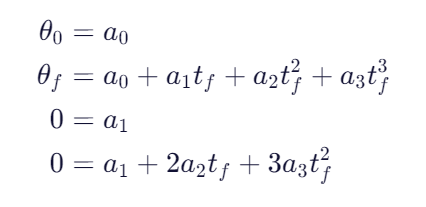
解得:
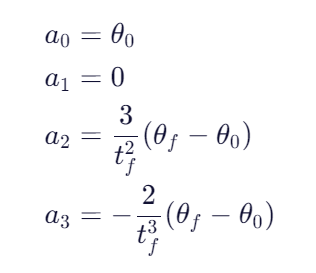
这样,插值表达式就可以完全由初末状态的约束表达了。输入任意时刻t,都能计算出每个关节的瞬时角度了。
Matlab实现
时间控制部分
我们再次明确:让机械臂末端从位姿 P1 平滑移动到 P2
这需要三个步骤:
空间路径规划->时间插值控制->逆解+可视化
我们先介绍几种常见时间控制插值算法,这些方法你可能没听过,但不要紧,现在只是让你知道有这些函数,是什么?至于是如何实现的,下面会讲。
对比三种"节奏"控制方式(插值方式)
| 节奏类型 | 代码 | 效果 |
|---|---|---|
| 匀速 | s = linspace(0,1,51) |
机器人匀速走,启停有冲击 |
| S形平滑 | t=linspace(0,3,51); s=tpoly(0,1,t); |
慢启动 → 快 → 慢停止 |
| 梯形速度 | t=linspace(0,3,51); s=lspb(0,1,t); |
加速 → 匀速 → 减速 |
linspace是一个均匀时间轴生成器,他会生成一个数组,在t0-t1这段时间中均匀插入n个时间节点,这些时间节点就是用于计算逆解的时间点。
但聪明的你意识到刚刚学到过线性插值效果不行。
于是考虑如何对时间进行五项式插值:
我们定义了一个函数映射,
P = tpoly(x1, x2, t)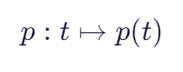
这个函数就是我们之前推导的三项式插值的拓展版------五项式插值。(推导用的关节坐标系,把θ换为笛卡尔坐标系的坐标即可构建这个映射)
"重新参数化"时间轴
想象你有一根均匀的时间轴:
t = [0.0, 0.1, 0.2, ..., 3.0] ← 均匀分布你想让机器人"慢启动 → 快 → 慢停止",就不能直接用这些 t 值去线性推进进度。
于是你用 tpoly 把 t 重新映射成一个新的进度 s:
s = tpoly(0,1,t) → [0.0, 0.001, 0.008, ..., 0.992, 0.999, 1.0]
Matlab
原始时间轴 t (均匀):
|----|----|----|----|----|----|----|----|----|----|
0 0.3 1.0 2.0 3.0
被 tpoly "扭曲" 成 s(t):
| | | | | | |
0 0.01 0.1 0.9 0.99 1.0
↖ S形曲线:开头密,中间疏,结尾密 ↗✅
tpoly就是一个"时间扭曲器"(Time Warper),把"均匀时间"扭曲成"S形进度"
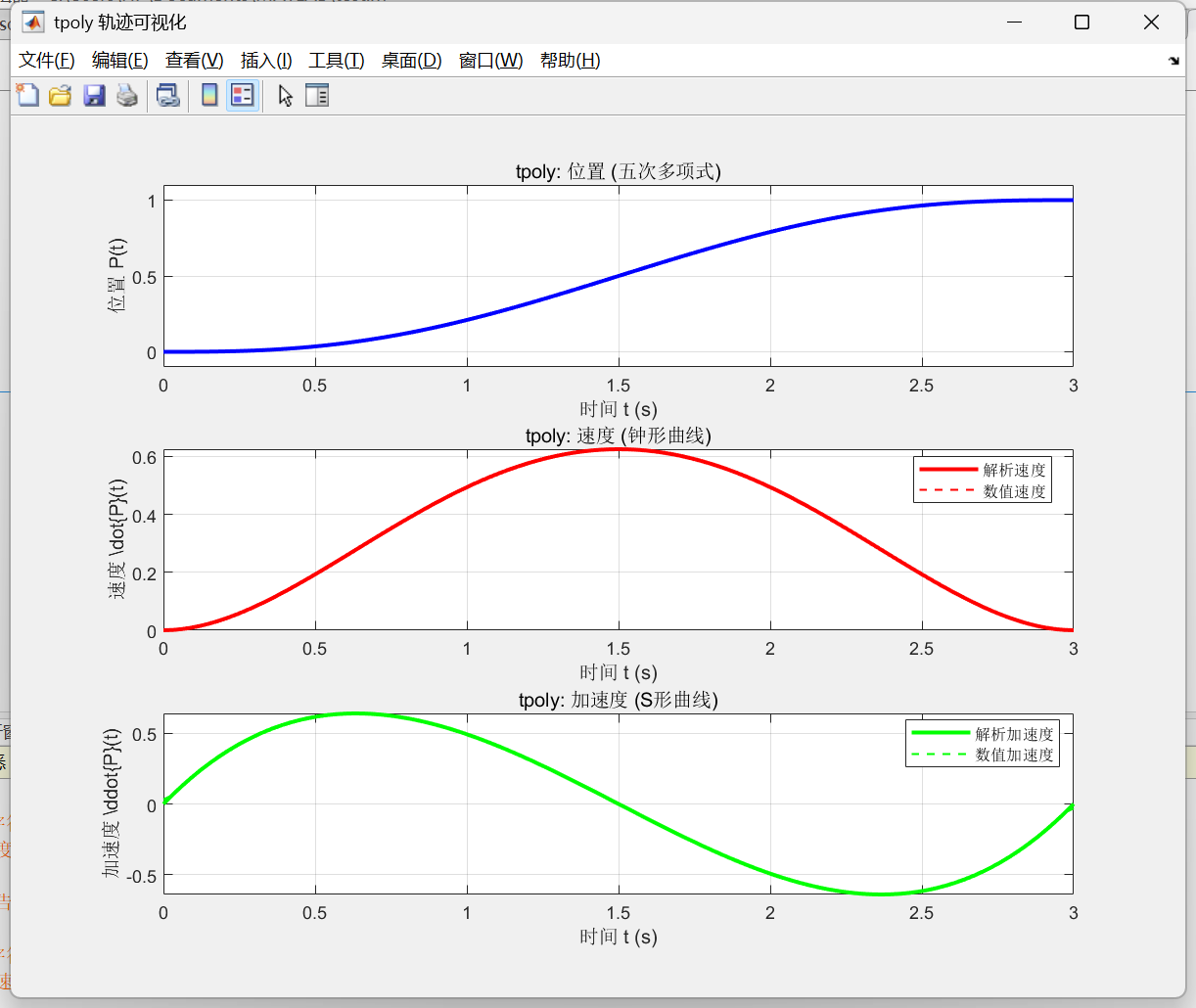
这样,我们就得到了一个五项式插值。
同理,你也想到了,不仅可以用tpoly来映射,还有可以用lspb来映射。
lspb(x1, x2, t) 将时间向量 t 通过一个"梯形速度"剖面,平滑地"映射"或"扭曲"到从 x1 到 x2 的值域上。
tpoly 是"S形扭曲",lspb 是"梯形速度扭曲",他能尽可能长时间保持最大速度。
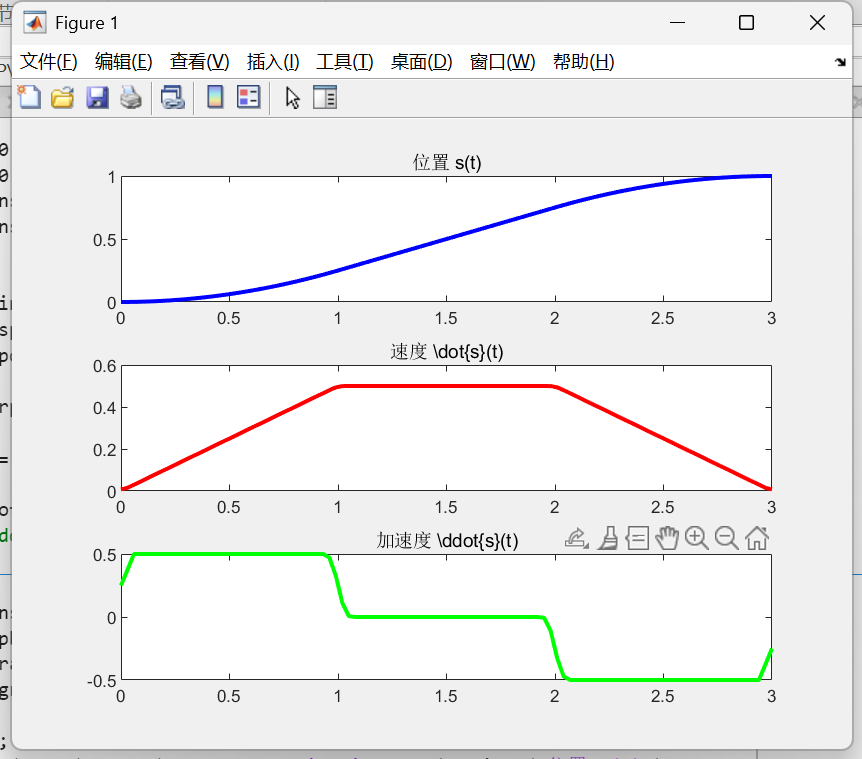
接下来,我们来看下这些函数如何实现的?
单个维度的时间控制------线性插值:linspace
插值linspace函数
"linspace" 这个名称来源于 "linear space" 的缩写,意味着该函数生成的是线性分布的点。
基本用法
以下是一个通用的例子:
- 起始值:ta
- 结束值:tb
- 点的数量:n
调用 linspace(ta, tb, n) 将返回一个数组,包含从 ta 到 tb 之间的 n 个等间隔数值。
因此t就是一个拥有n个插值点的数组。这里意味着从ta到tb间均匀插入n个时间点。
这个函数决定了整个运动控制的时间从何时开始,何时结束,有几次插值。
单个维度的时间控制------五次多项式插值:tpoly
这是一个非常强大的插值生成器,他能生成位置、速度、加速度的插值函数
主要有两种参数模板:
✅ 形式1:使用时间向量(推荐用于真实时间仿真)
[P, dP, ddP] = tpoly(q0, qf, t);这种形式q0是起始坐标,qf是终点坐标,t是时间向量,允许自定义时序插值。比如我们希望在0-3秒内均匀时间点插值,那么可以这样写(见注释):
Matlab
t = linspace(0, 3, 51); % 在 0 到 3 秒内,取 51 个时间点
[P, dP, ddP] = tpoly(q0, qf, t); % 从 q0 到 qf,在 3 秒内完成上面是我们刚刚提到的"映射为五项式"的形式,tpoly还提供另一种形式:
✅ 形式2:指定采样点数(常用于归一化进度生成)
这种形式没有t向量,意味着它将在1秒内完成,无法像时间向量一样来调控采样时序。
[P, dP, ddP] = tpoly(q0, qf, N, a0, af);此外,要强调的是,matlab允许函数返回多个值,你可以选择性接受。
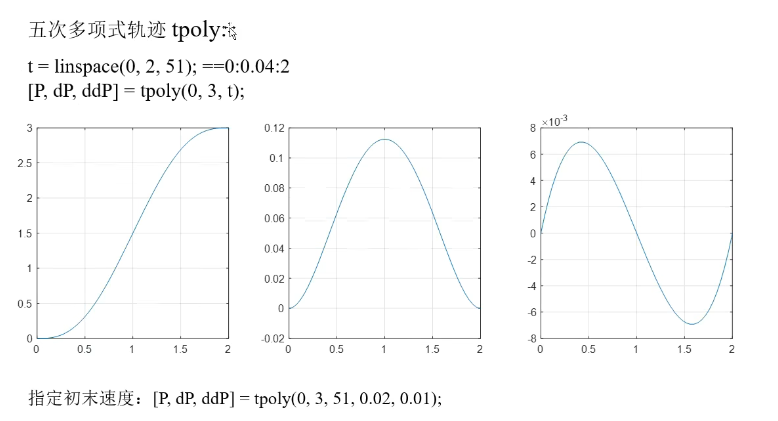
我们给定在0~2秒内进行51次插值,也就是每0.04秒执行一次插值。
单个维度的时间控制------混合曲线插值:lspb
同上,只是把插值映射函数改为了lspb。
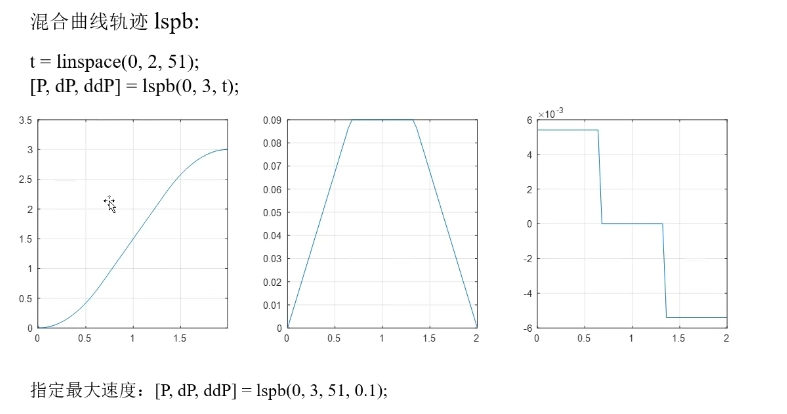
我们的机器人是在多维空间中运作的,上文这些时间控制仅用于单个维度,因此我们还需要扩展到多个维度的控制------
多维轨迹规划=mtraj+@插值方法
很好理解,mtraj相当于对各个维度都采用@XX这种插值控制方式,比如我们刚学的lspb或tpoly。
Matlab
p = mtraj(@tpoly, p0, pf, t);此时不用一个维度一个维度写tpoly/lspb的具体参数了,但依然需要传入时间轴t,决定了花多久允许完整个过程。mtraj 会把时间向量 t 传给每一个 @tpoly,让它们在指定的时间点上完成插值。
🔹 参数1:@f ------ "时间规划器":每个维度怎么随时间变化?
| 参数 | 控制什么? | 常见值 |
|---|---|---|
@f |
位置如何随时间变化 | @tpoly:五次多项式(S形) @lspb:梯形速度 |
🔹 参数2:p0 和 pf ------ 起点和终点的坐标+姿态(向量)
| 参数 | 控制什么? | 例子 |
|---|---|---|
p0 |
起点的多维值 | [0.7, -0.5, 0] / [0, 0] |
pf |
终点的多维值 | [0.7, 0.5, 0.5] / [pi/2, pi/4] |
🔹 参数3:t ------ 时间轴:在哪些时间点上计算轨迹?
| 参数 | 控制什么? | 例子 |
|---|---|---|
t |
时间点序列,表示"在哪些时刻计算位置" | t = linspace(0, 2, 51) / ``t = 0:0.04:2 |
比如下面,使用多维轨迹插值函数mtraj,选用插值处理方法为@tpoly五项式插值,第四参数传入时间轴,第二三参数是初末位置。很好理解。
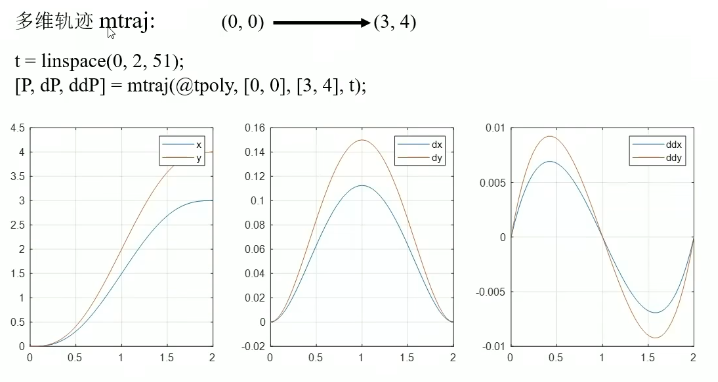
这个不属于时间/空间规划,只是作为扩展。为了逻辑连贯,你可以先跳过。
多段轨迹规划
mstraj函数用于处理多端轨迹规划问题,他有7个参数,其中QDMAX和TSEG是冲突参数,只能指定其一。
1. WP (Waypoints)
- 含义:轨迹中的节点。
2. QDMAX (Maximum Velocity)【与下面参数冲突】
- 含义:最大速度限制。
3. TSEG (Segment Times)【与上面参数冲突】
- 含义:每个轨迹段的持续时间。
4. Q0 (Initial Position)
- 含义:初始位置。
5. DT (Sampling Time)
- 含义:采样时间间隔。
6. TACC (Acceleration Time)
- 含义:加速和减速时间。
7. OPTIONS (Optional Parameters)
- 含义:其他可选参数。
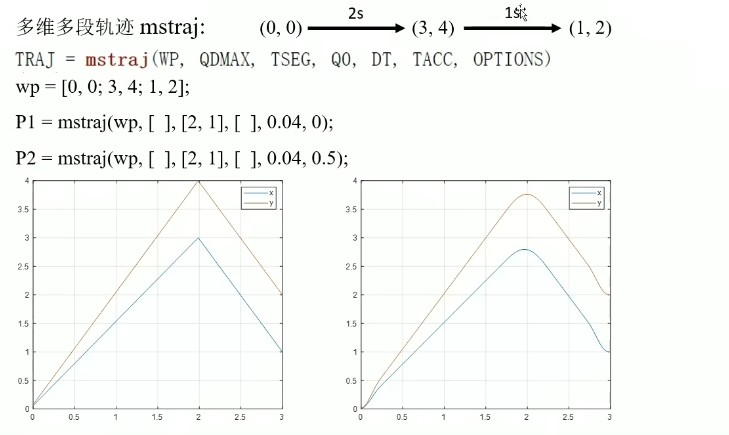
P1代表以wp为路径节点,最大速度置为空,两段路径的花费时间分别是2和1s,Q0初始位置为空,默认为WP的(0,0),间隔为0.04s,加速时间为0
P2代表以wp为路径节点,最大速度置为空,两段路径的花费时间分别是2和1s,Q0初始位置为空,默认为WP的(0,0),间隔为0.04s,加速时间为0.5
显然,图一加速时间为0,因此存在拐点,加速度瞬间从2变到-2,是不合实际的。
而图二的加速时间是0.5s,可以看到拐点前后有大约0.25s的弯曲,此时加速度就是连续的了。
之前我们已经完成了时间规划与插值了,接下来要完成空间规划以及在之前的时间插值点计算变换矩阵的操作了。
★ 三维空间的位置轨迹规划
欢迎来到真正的正文!
在真正进行规划的时候要有这样的意识:**尽管在笛卡尔空间中轨迹是连续的,可能在关节空间内,关节变量并非连续的!**因此,下面从笛卡尔空间插值讲解到关节空间插值的解决方案。
题目:演示从P1到P2位置的插值流程,包括模型描述、轨迹规划与逆运动学求解以及轨迹可视化。
基础不带插值的代码如下,对P1,P2分别转化为变换矩阵,再乘以trotx(180)。因为默认工具坐标系与基坐标系共轴,因此是朝上的,我们尽量从上方靠近目标点,也就是朝下的,要乘以trotx(180)。你可以删去试试。
Matlab
%% 定义五自由度机械臂
L(1) = Link('revolute','d',0.216,'a',0,'alpha',pi/2);
L(2) = Link('revolute','d',0,'a',0.5,'alpha',0,'offset',pi/2);
L(3) = Link('revolute','d',0,'a',sqrt(0.145^2+0.42746^2),'alpha',0, 'offset', -atan(427.46/145));
L(4) = Link('revolute','d',0,'a',0,'alpha',pi/2,'offset', atan(427.46/145));
L(5) = Link('revolute', 'd', 0.258, 'a', 0, 'alpha', 0);
Five_dof = SerialLink(L, 'name', '5-dof');
Five_dof.base = transl(0, 0, 0.28);
%% 生成笛卡尔空间轨迹
P1 = [0.7, -0.5, 0];
P2 = [0.7, 0.5, 0.5];
T1=transl(P1)*trotx(180);
T2=transl(P2)*trotx(180);
q1=Five_dof.ikunc(T1);
q2=Five_dof.ikunc(T2);
Five_dof.plot(q1);
pause;
Five_dof.plot(q2);我们来做空间轨迹规划吧,实际上,具体如何做已经不需要我们完成了,matlab的机器人工具箱提供了封装好的函数,我们只要会用即可。
空间规划有两种形式,一种是在笛卡尔空间做空间插值,另一种是在关节空间内做。
笛卡尔空间规划
法一:mtraj笛卡尔空间内插值,并在各点转化为变换矩阵,接着对各点计算逆解,得到关节变量变化。

具体步骤分析
1. P1/P2 到 Traj
- 使用
mtraj函数生成从起始点P1到目标点P2的平滑轨迹Traj。这一步确保了在笛卡尔空间中的轨迹是平滑和连续的。
2. Traj 到 T
- 使用
transl函数将轨迹中的每个位置点转换为齐次变换矩阵T。
3. T 到 Qtraj
- 使用
ikunc函数根据齐次变换矩阵T计算出对应的关节角度Qtraj。这一步是关键,因为逆运动学求解可能会引入不连续性。
运行代码
这里利用mtraj规划器,采用tpoly五项式的空间插值方式,采用均分时间的速度控制方式
Matlab
%% 定义五自由度机械臂
L(1) = Link('revolute','d',0.216,'a',0,'alpha',pi/2);
L(2) = Link('revolute','d',0,'a',0.5,'alpha',0,'offset',pi/2);
L(3) = Link('revolute','d',0,'a',sqrt(0.145^2+0.42746^2),'alpha',0, 'offset', -atan(427.46/145));
L(4) = Link('revolute','d',0,'a',0,'alpha',pi/2,'offset', atan(427.46/145));
L(5) = Link('revolute', 'd', 0.258, 'a', 0, 'alpha', 0);
Five_dof = SerialLink(L, 'name', '5-dof');
Five_dof.base = transl(0, 0, 0.28);
%%
P1 = [0.7, -0.5, 0];
P2 = [0.7, 0.5, 0.5];
t = linspace(0, 2, 51);
Traj = mtraj(@tpoly, P1, P2, t);
n = size(Traj, 1);
T = zeros(4, 4, n);
for i = 1:n
T(:, :, i) = transl(Traj(i, :)) * trotx(180);
end
Qtraj = Five_dof.ikunc(T);
Five_dof.plot(Qtraj, 'trail', 'b');
Five_dof.plot(Qtraj, 'movie', 'trail.gif');核心代码
Matlab
Traj = mtraj(@tpoly, P1, P2, t);
n = size(Traj, 1);
T = zeros(4, 4, n);
for i = 1:n
T(:, :, i) = transl(Traj(i, :)) * trotx(180);
end这里用mtraj使用五项式插值的空间插值方式得到了插值矩阵Traj,然后对每个Traj进行逆解,得到变换矩阵数组T,并把z轴转到下面。
运行效果
关节变量变化
小技巧:运行节
%%是分节符,比如接下来我需要绘制关节变量的变化趋势,不需要重头执行,而是可以在前面代码最后"追加节"
在上面代码的最后追加以下内容:
Matlab
%%
hold on
plot(t, Traj(:, 1), '.-', 'linewidth', 1);
plot(t, Traj(:, 2), '.-', 'linewidth', 1);
plot(t, Traj(:, 3), '.-', 'linewidth', 1);
grid on
legend('x', 'y', 'z');
xlabel('time');
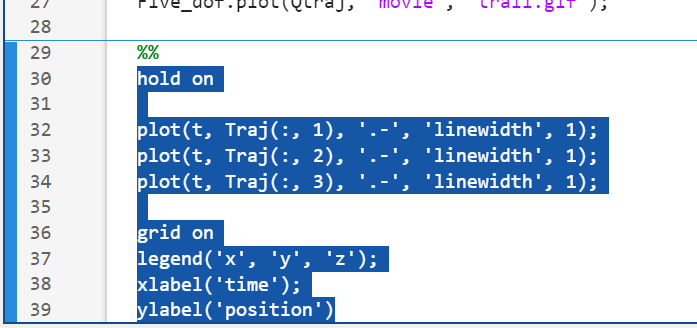
ylabel('position')点击最后这段代码,会在列选出现蓝色条,代表选中当前节了
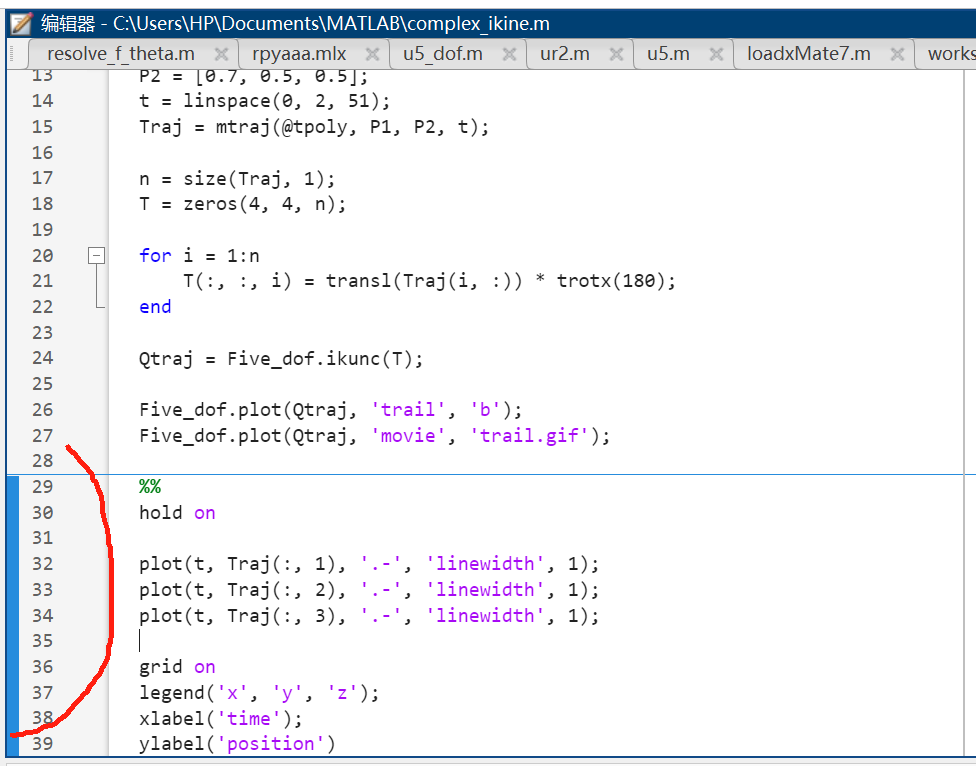
点击"运行节",就只会运行选中部分的代码:
小技巧:执行所选内容
"运行节"是一种方案,假如我们只是要运行一行(或多行)呢?
这个时候可以选中,然后按"F9"。
或者选中所需要运行的内容,右键,点击"在命令行窗口中执行所选内容"
因此"运行节"的操作也可以:
选中需要运行的内容
按"F9"或点击"在命令行窗口中执行所选内容"
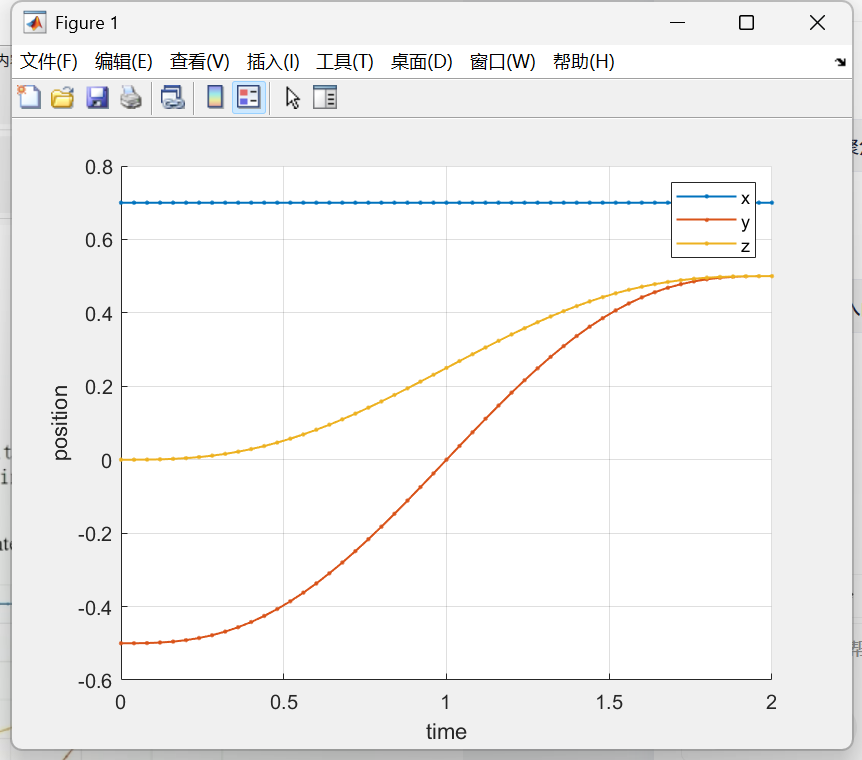
关节变量轨迹
以上"运行节"和"运行所选内容"都能得到这张图:由于是在笛卡尔空间中做的插值,因此xyz三维上都是连续的。
法二:位姿插值函数trinterp
🔹 参数1:T1 和 T2 ------ 起点和终点的"完整姿势"
🔹 参数2:M ------ 选用的空间插值函数
比如看下面,
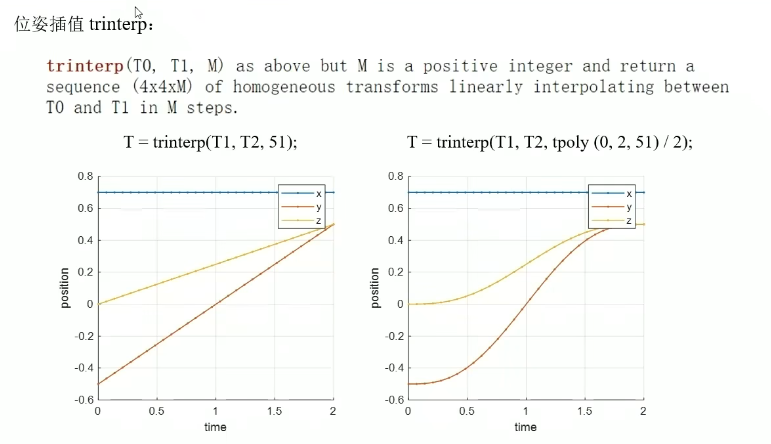
运行代码
Matlab
%% 定义五自由度机械臂
L(1) = Link('revolute','d',0.216,'a',0,'alpha',pi/2);
L(2) = Link('revolute','d',0,'a',0.5,'alpha',0,'offset',pi/2);
L(3) = Link('revolute','d',0,'a',sqrt(0.145^2+0.42746^2),'alpha',0, 'offset', -atan(427.46/145));
L(4) = Link('revolute','d',0,'a',0,'alpha',pi/2,'offset', atan(427.46/145));
L(5) = Link('revolute', 'd', 0.258, 'a', 0, 'alpha', 0);
Five_dof = SerialLink(L, 'name', '5-dof');
Five_dof.base = transl(0, 0, 0.28);
%%
P1 = [0.7, -0.5, 0];
P2 = [0.7, 0.5, 0.5];
T1=transl(P1)*trotx(180);
T2=transl(P2)*trotx(180);
t = linspace(0, 2, 50);
T_interp = trinterp(T1, T2, t/2); % 直接对两个位姿插值
Qtraj = Five_dof.ikunc(T_interp);
Five_dof.plot(Qtraj, 'trail', 'b');
Five_dof.plot(Qtraj, 'movie', 'trinterp_trail.gif');核心代码
Matlab
t = linspace(0, 2, 50);
T_interp = trinterp(T1, T2, t/2); % 直接对两个位姿插值运行效果
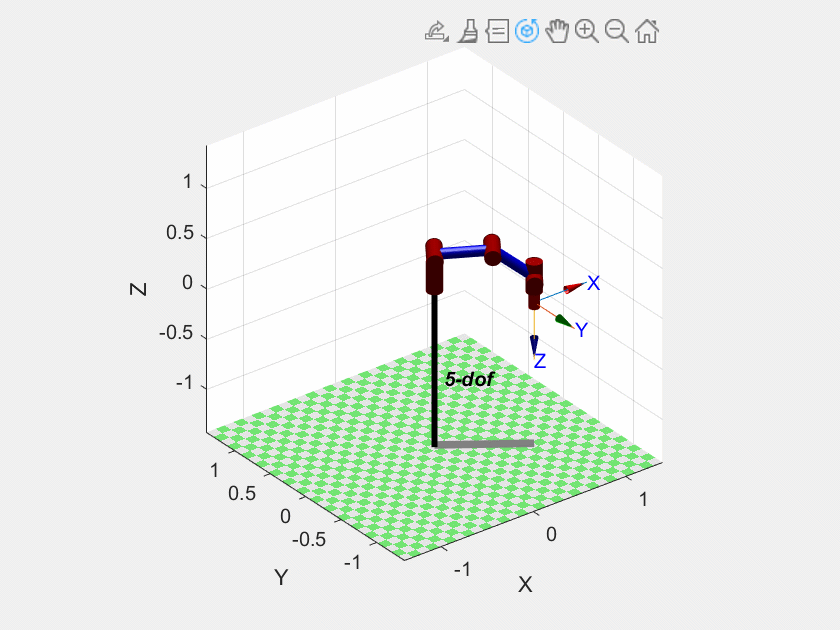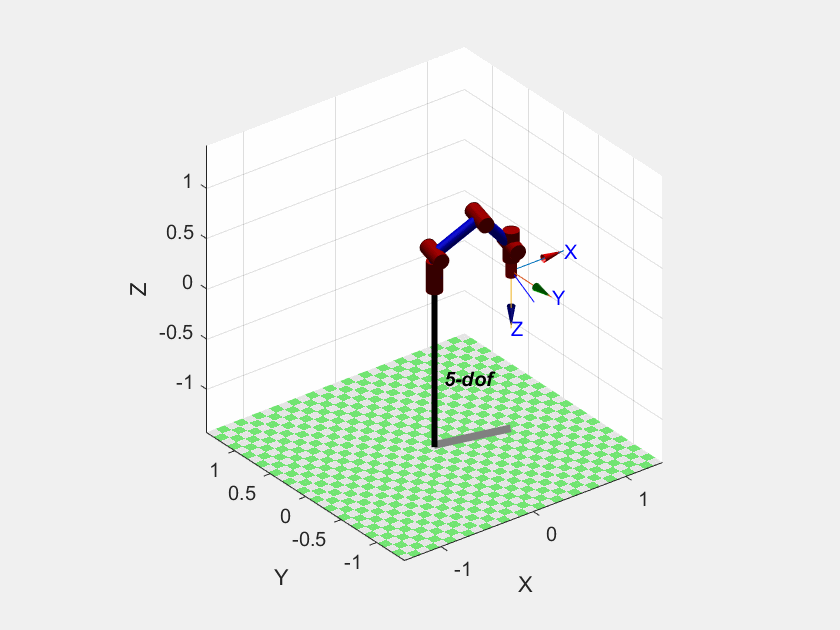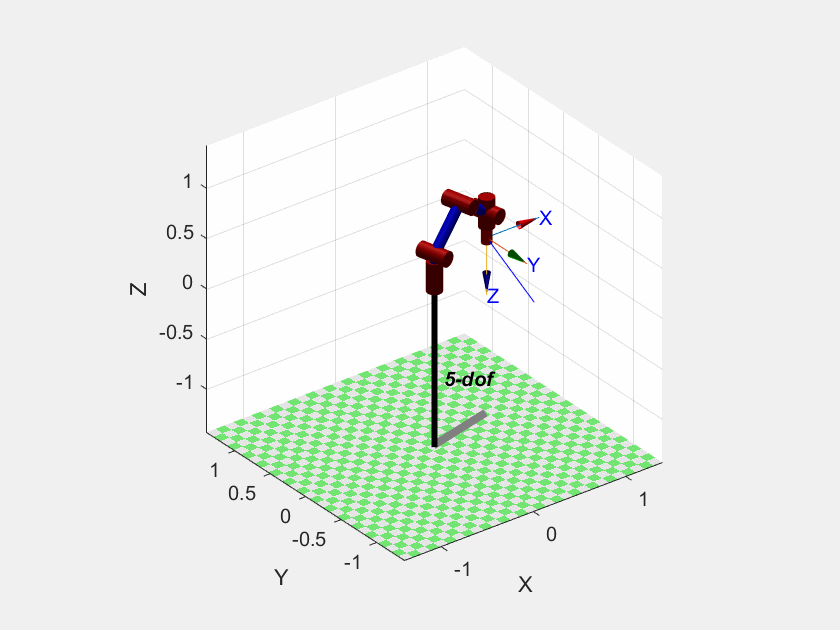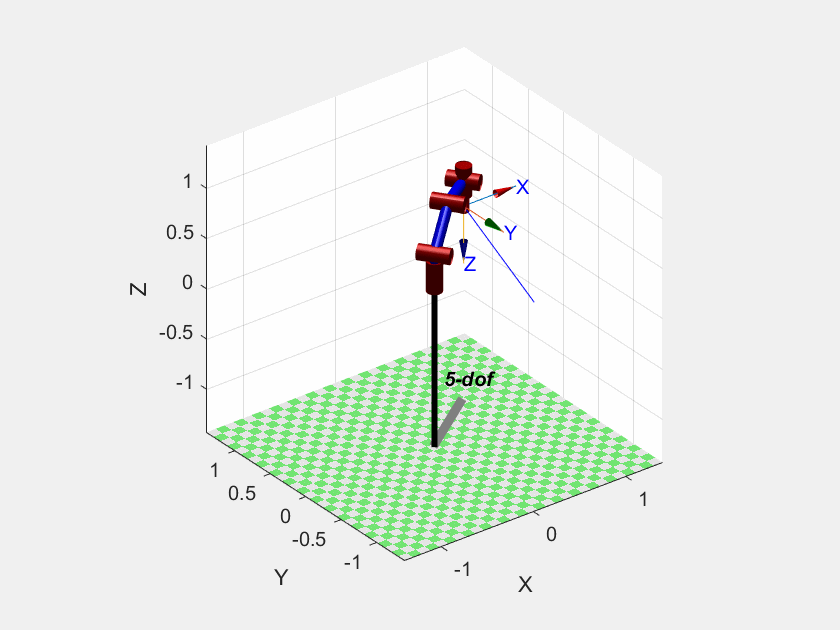
运动曲线
为了看出选用的插值函数M到底对运动曲线有什么影响,我们在后面也添上这段代码
Matlab
%%
P_liner = transl(T_interp);
hold on
plot(t, P_liner(:, 1), '.-', 'linewidth', 1);
plot(t, P_liner(:, 2), '.-', 'linewidth', 1);
plot(t, P_liner(:, 3), '.-', 'linewidth', 1);
grid on
legend('x', 'y', 'z');
xlabel('time');
ylabel('position');由于上面代码用的普通的线性插值,因此笛卡尔空间的运动曲线都是线性的
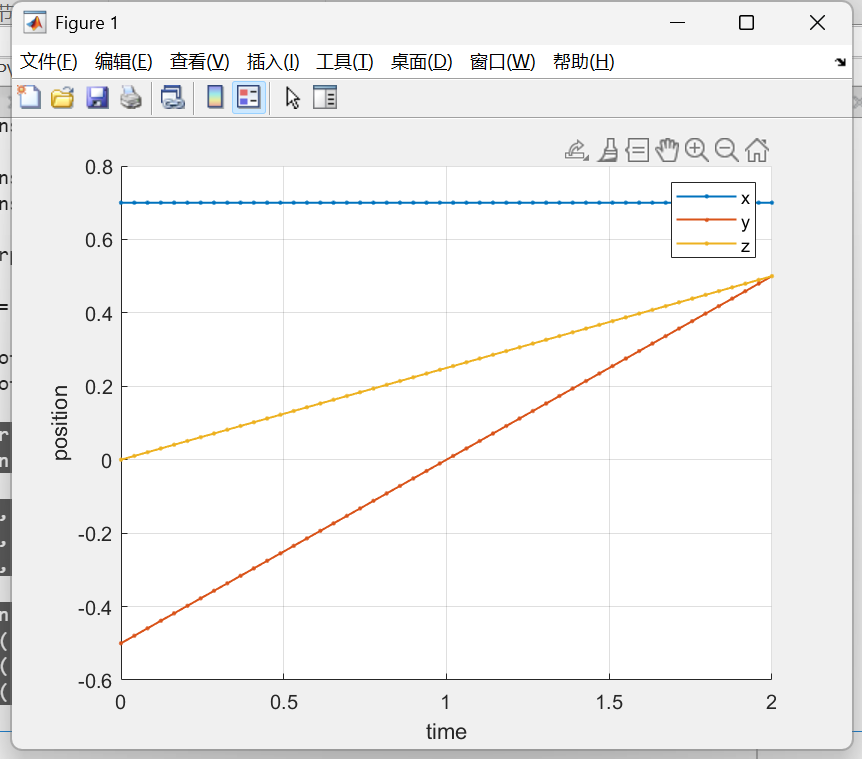
我们试试用tpoly看看会不会呈现不一样的效果:
把这一句:
Matlab
T_interp = trinterp(T1, T2, t/2); % 直接对两个位姿插值替换为:
Matlab
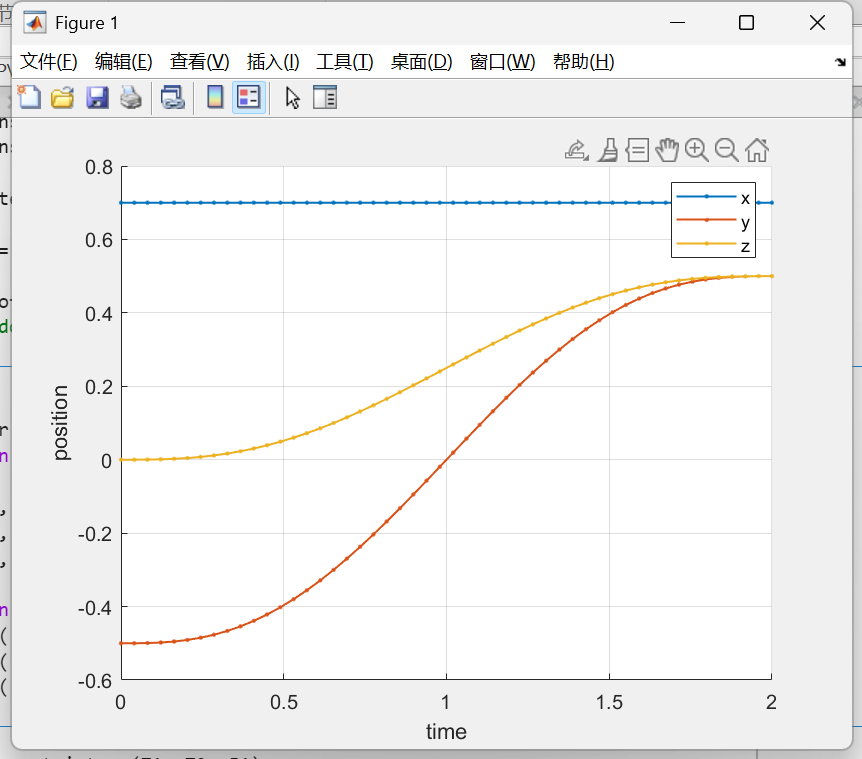
T_interp = trinterp(T1, T2, tpoly(0,2,50)/2); % 直接对两个位姿插值重新运行这一节,然后运行绘图那一节:
显然我们的五项式插值使得运动曲线变弯了,M作为可以任意选择的时间插值函数,就是matlab模块化的特征。
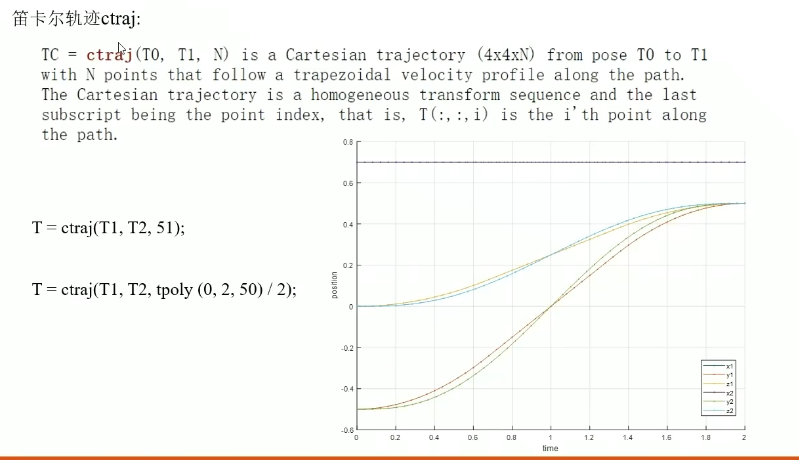
法三:笛卡尔轨迹插值函数ctraj
同上,基本是一样的,把上文trinterp替换为ctraj即可。
运行代码
Matlab
%% 定义五自由度机械臂
L(1) = Link('revolute','d',0.216,'a',0,'alpha',pi/2);
L(2) = Link('revolute','d',0,'a',0.5,'alpha',0,'offset',pi/2);
L(3) = Link('revolute','d',0,'a',sqrt(0.145^2+0.42746^2),'alpha',0, 'offset', -atan(427.46/145));
L(4) = Link('revolute','d',0,'a',0,'alpha',pi/2,'offset', atan(427.46/145));
L(5) = Link('revolute', 'd', 0.258, 'a', 0, 'alpha', 0);
Five_dof = SerialLink(L, 'name', '5-dof');
Five_dof.base = transl(0, 0, 0.28);
%%
P1 = [0.7, -0.5, 0];
P2 = [0.7, 0.5, 0.5];
T1=transl(P1)*trotx(180);
T2=transl(P2)*trotx(180);
t = linspace(0, 2, 50);
T_ctraj = ctraj(T1, T2, t/2); % 直接对两个位姿插值
Qtraj = Five_dof.ikunc(T_ctraj);
Five_dof.plot(Qtraj, 'trail', 'b');
Five_dof.plot(Qtraj, 'movie', 'ctraj_trail.gif');核心代码
把前面的trinterp替换为笛卡尔插值ctraj即可
Matlab
t = linspace(0, 2, 50);
T_ctraj = ctraj(T1, T2, t/2); % 直接对两个位姿插值运行效果
关节变量变化
和上文一样,把T_trinterp替换为T_ctraj即可
Matlab
%%
P_liner = transl(T_ctraj);
hold on
plot(t, P_liner(:, 1), '.-', 'linewidth', 1);
plot(t, P_liner(:, 2), '.-', 'linewidth', 1);
plot(t, P_liner(:, 3), '.-', 'linewidth', 1);
grid on
legend('x', 'y', 'z');
xlabel('time');
ylabel('position');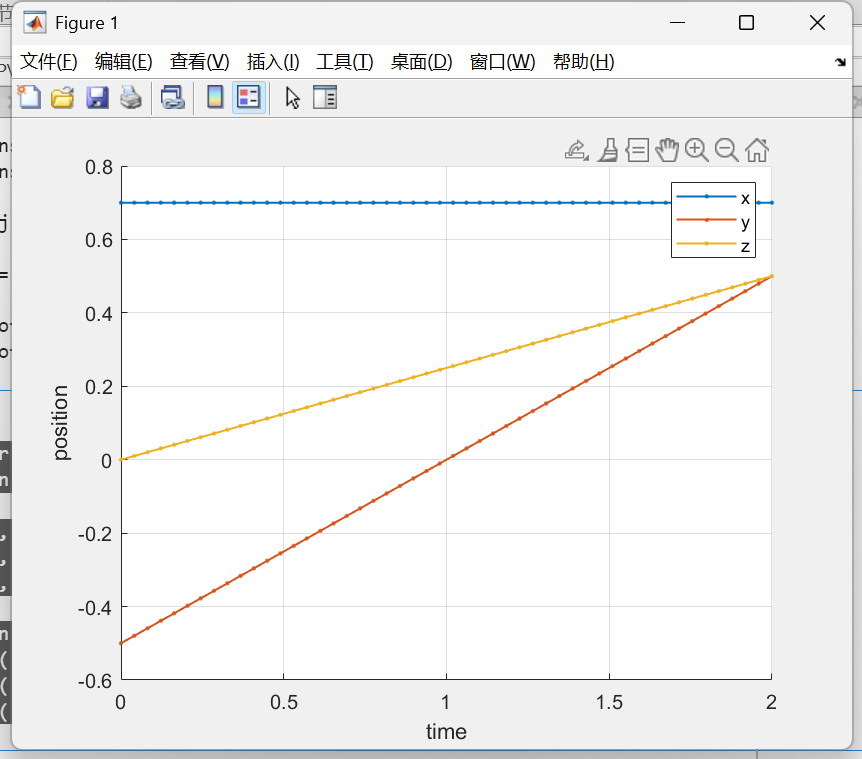
同理,如果把:
Matlab
T_ctraj = ctraj(T1, T2, t/2); % 直接对两个位姿插值替换为:
Matlab
T_ctraj = ctraj(T1, T2, tpoly(0,2,50)/2); % 直接对两个位姿插值依然可以得到弯曲的图像。
至此,对于轨迹规划对于位置的处理主体全部结束。
接下来我们会学习如何处理姿态的轨迹规划。
★ 三维空间的姿态轨迹规划
我们继续,
对于姿态的处理,和位置其实一样,依然可以用最朴素的方式,把初末状态的姿态也用tr2rpy转化为rpy角,然后用mtraj+@XX的方式得到姿态的变换矩阵,再求逆,得到关节变量。

但是,问题这时候出现了!

机械臂以一种极其扭曲抽象怪异猎奇不适不安恐惧的轨迹和姿态走到了终点。

从命令行我们也能看出,好几处位姿到达奇异点,导致关节变量突变,这是极其容易损坏机械臂的。
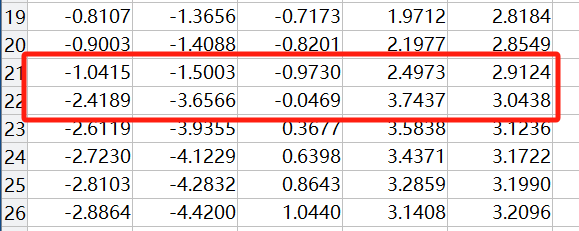
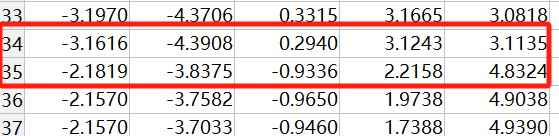
这是因为,在笛卡尔空间规划路径,再通过逆解映射到关节空间。即使末端轨迹连续,但由于逆解不唯一,可能导致关节角度突变。
我们再试试trinterp:
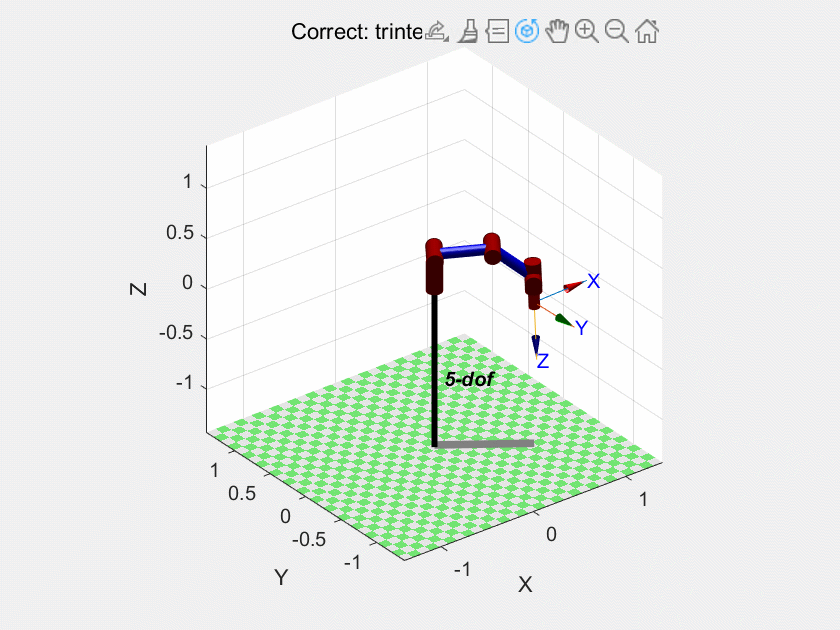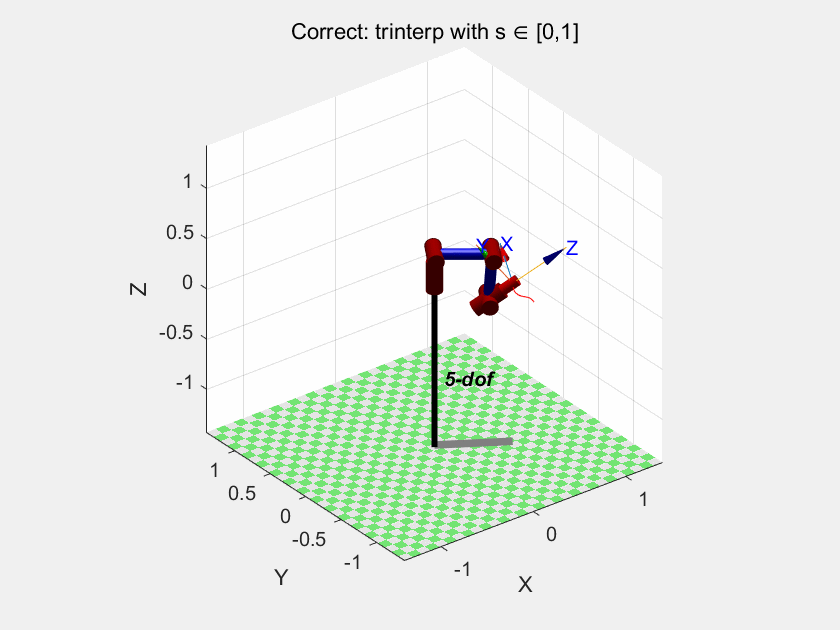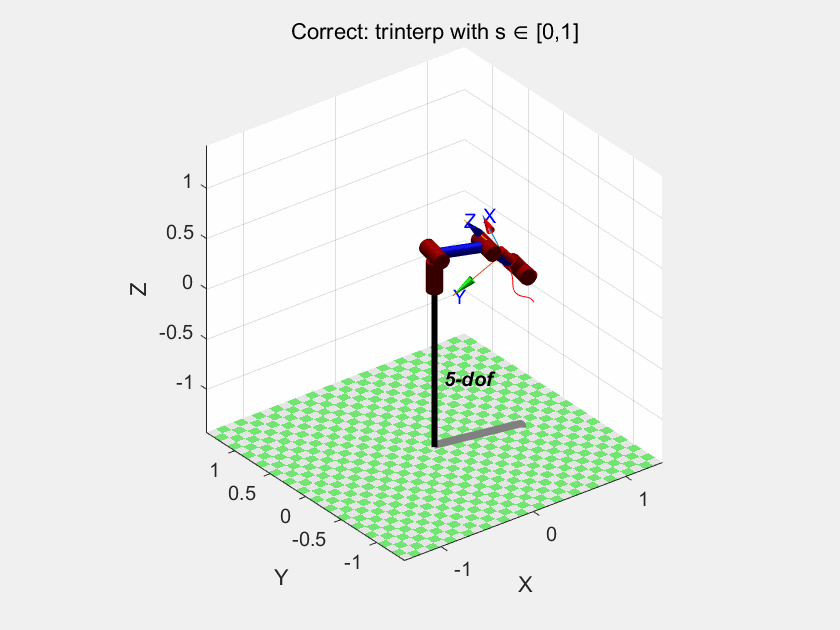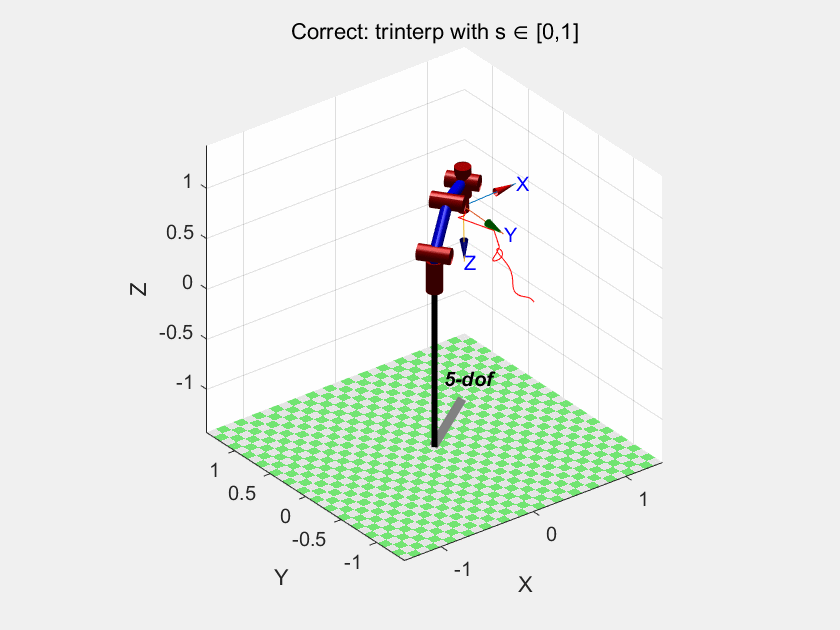
以及ctraj:
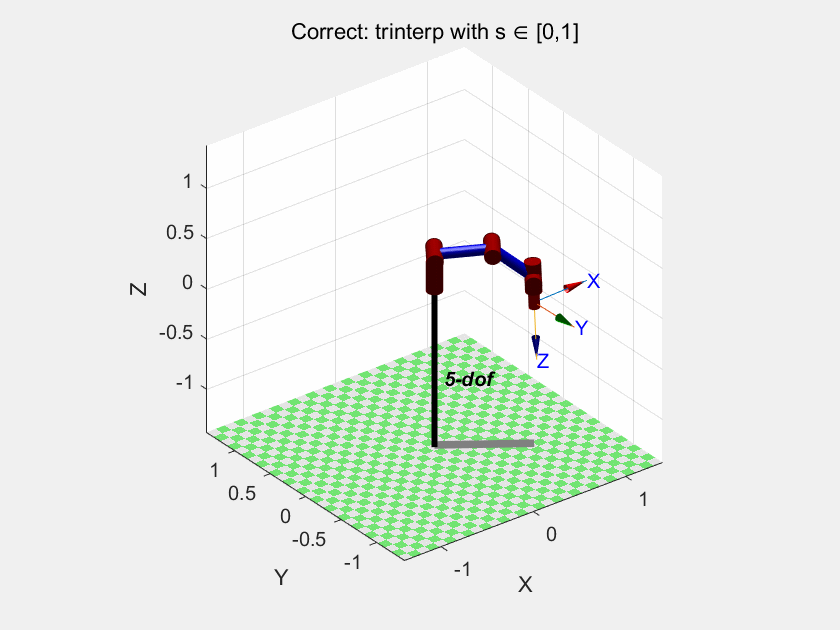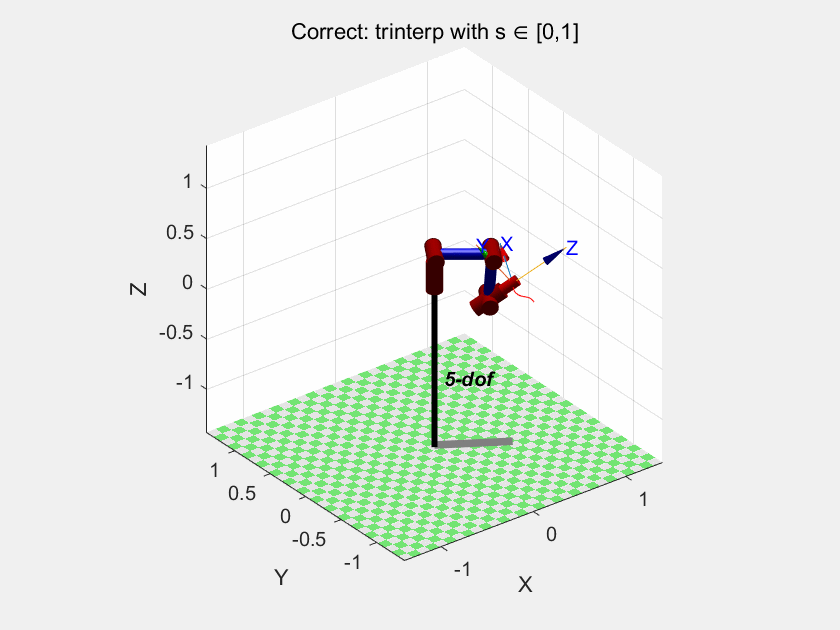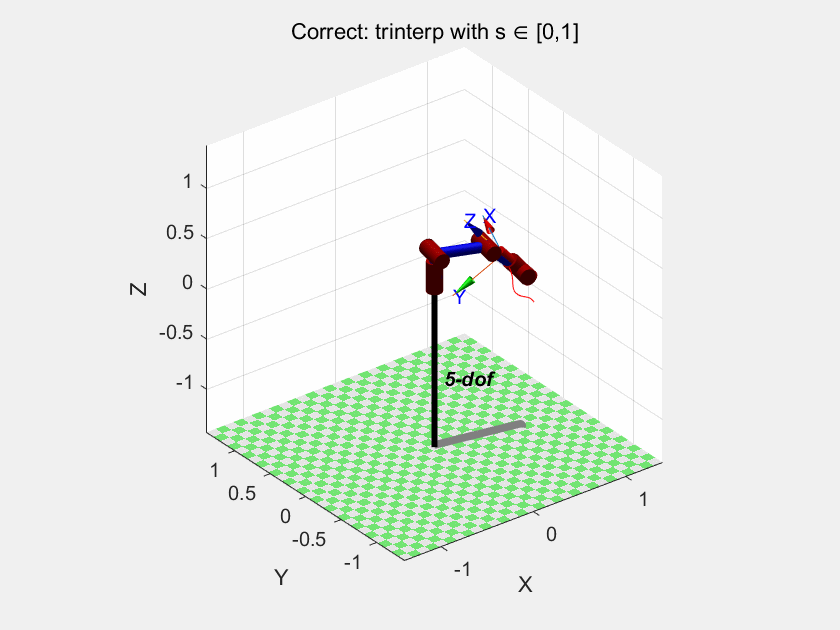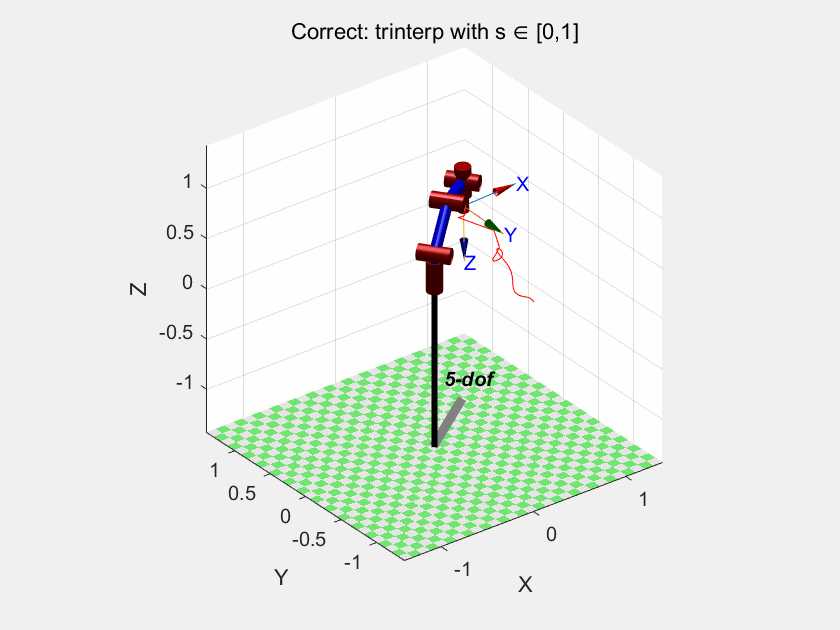
我们可以得出结论:trinterp 和 ctraj 是在笛卡尔空间插值的,因此它们也无法保证关节空间的连续性或最优性。
至于视频中up为何能实现直线旋转移动过去我也没有复现出来。应该是修改了角度。
下面这个是按照这个参数设置的,效果不错:
Matlab
rpy1_base = [0, 150, 30];
rpy2_base = [90, 200, 190];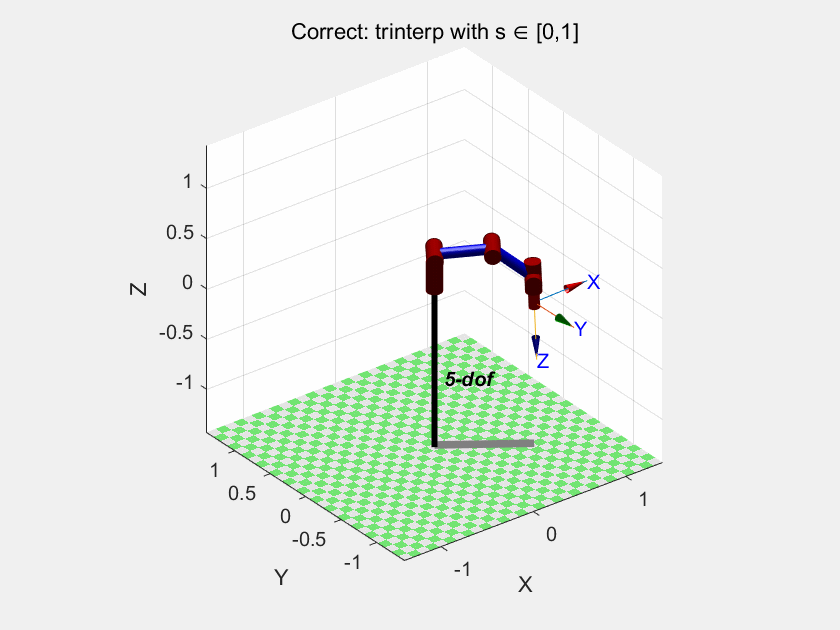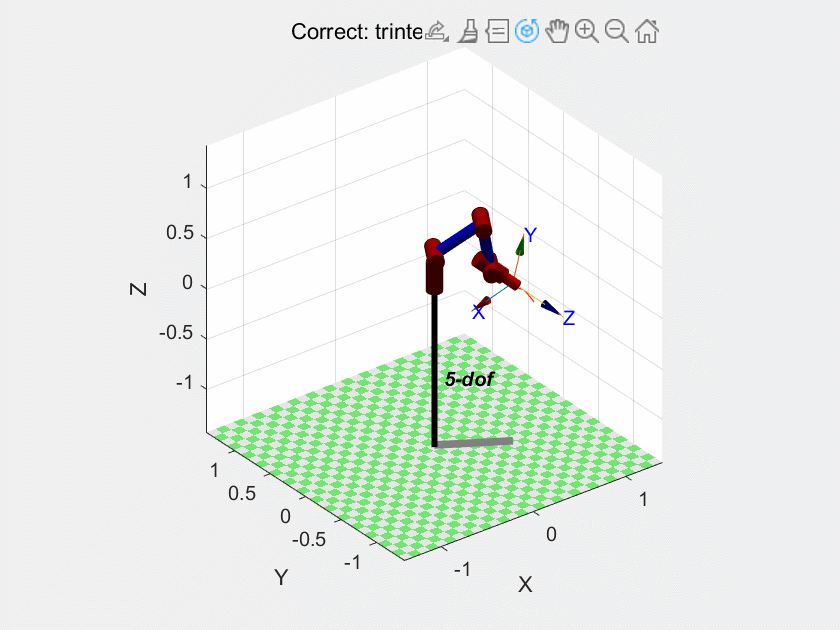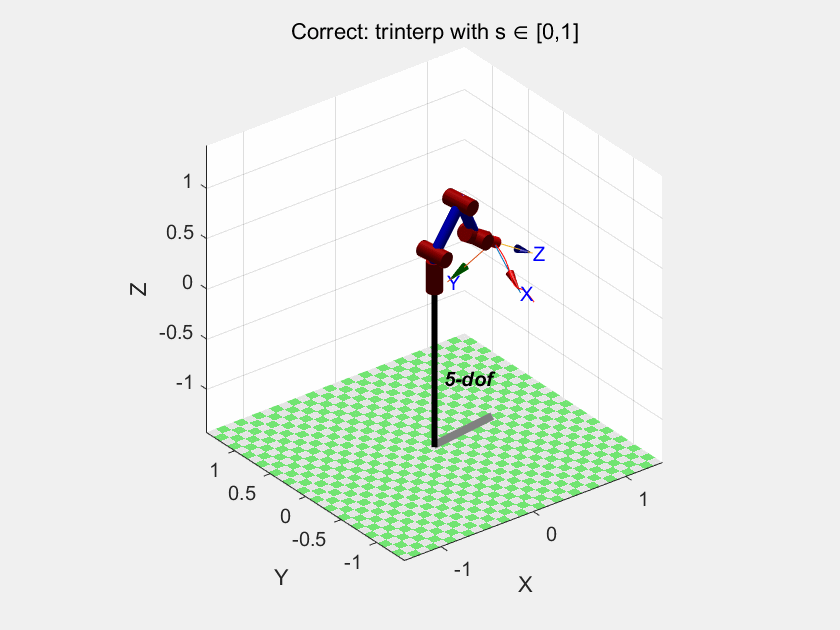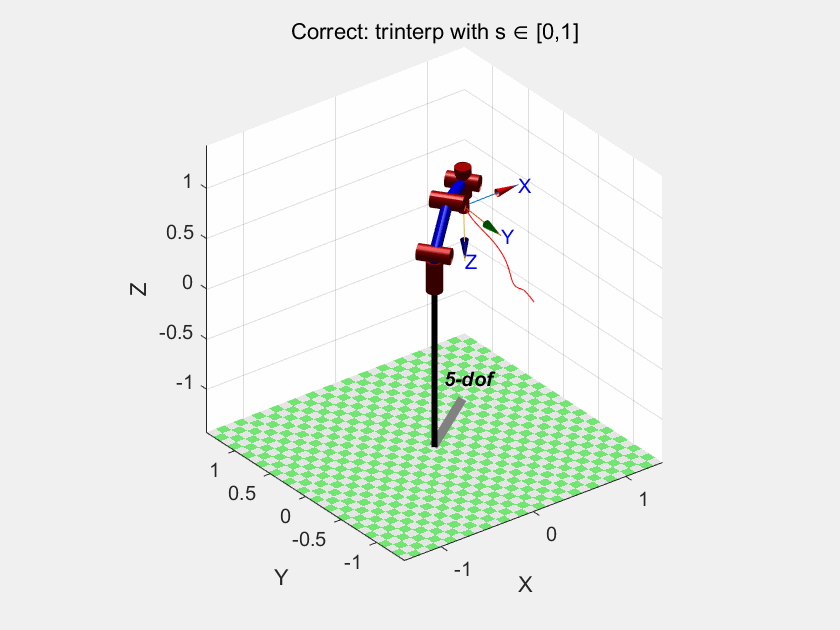
完整代码:
Matlab
%% 定义五自由度机械臂
L(1) = Link('revolute','d',0.216,'a',0,'alpha',pi/2);
L(2) = Link('revolute','d',0,'a',0.5,'alpha',0,'offset',pi/2);
L(3) = Link('revolute','d',0,'a',sqrt(0.145^2+0.42746^2),'alpha',0, 'offset', -atan(427.46/145));
L(4) = Link('revolute','d',0,'a',0,'alpha',pi/2,'offset', atan(427.46/145));
L(5) = Link('revolute', 'd', 0.258, 'a', 0, 'alpha', 0);
Five_dof = SerialLink(L, 'name', '5-dof');
Five_dof.base = transl(0, 0, 0.28);
%% 设置初始和目标位姿(z轴朝下)
P1 = [0.7, -0.5, 0];
P2 = [0.7, 0.5, 0.5];
rpy1_base = [0, 150, 30];
rpy2_base = [90, 200, 190];
T1_orient = rpy2tr(deg2rad(rpy1_base)) ;
T2_orient = rpy2tr(deg2rad(rpy2_base)) ;
T1 = transl(P1) *trotx(180)* T1_orient;
T2 = transl(P2) *trotx(180)* T2_orient;
%% ✅ 正确使用 trinterp
s = linspace(0, 1, 51); % 进度参数 [0,1]
T_traj = trinterp(T1, T2, s); % SE(3) 插值
%% 逆解与可视化
q_traj = Five_dof.ikunc(T_traj);
figure;
Five_dof.plot(q_traj, 'trail', 'r');
title('Correct: trinterp with s ∈ [0,1]');
Five_dof.plot(q_traj, 'movie', 'ctraj_trail.gif');解决关节空间内突变问题
解决方案呢?
本质上说,如果在笛卡尔空间就进行轨迹规划,那么之后才会进行对应关节空间求解,这是很容易造成关节空间不连续的突变的。 而如果先把初末位姿直接先求逆解,得到关节空间的初末位姿再在关节空间进行轨迹规划,就能避免这个问题
恭喜你,发现了
对变换矩阵进行插值的函数------
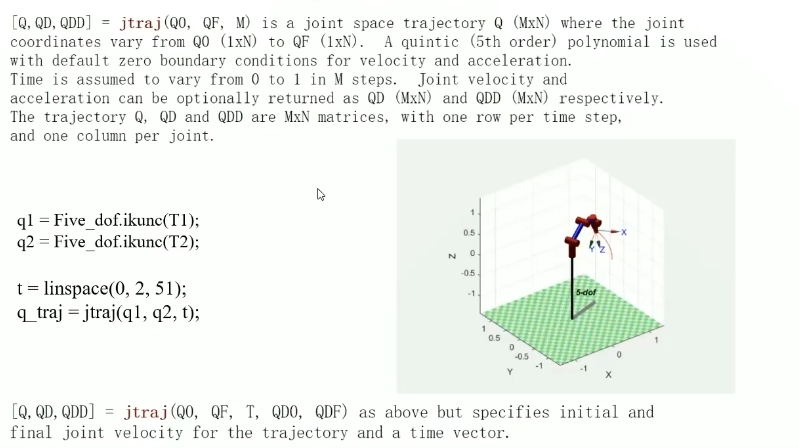
关节空间插值规划器jtraj
运行代码
Matlab
%% 定义五自由度机械臂
L(1) = Link('revolute','d',0.216,'a',0,'alpha',pi/2);
L(2) = Link('revolute','d',0,'a',0.5,'alpha',0,'offset',pi/2);
L(3) = Link('revolute','d',0,'a',sqrt(0.145^2+0.42746^2),'alpha',0, 'offset', -atan(427.46/145));
L(4) = Link('revolute','d',0,'a',0,'alpha',pi/2,'offset', atan(427.46/145));
L(5) = Link('revolute', 'd', 0.258, 'a', 0, 'alpha', 0);
Five_dof = SerialLink(L, 'name', '5-dof');
Five_dof.base = transl(0, 0, 0.28);
P1 = [0.7, -0.5, 0];
P2 = [0.7, 0.5, 0.5];
rpy1_base = [0, 150, 30];
rpy2_base = [90, 200, 190];
T1_orient = rpy2tr(deg2rad(rpy1_base));
T2_orient = rpy2tr(deg2rad(rpy2_base));
T1 = transl(P1) * trotx(180) * T1_orient; % 注意:pi 弧度 = 180°
T2 = transl(P2) * trotx(180) * T2_orient;
% 1. 求起终点关节角(可加初值避免跳解)
q1 = Five_dof.ikunc(T1);
q2 = Five_dof.ikunc(T2);
% 2. 关节空间插值
s = linspace(0, 1, 51);
q_traj = jtraj(q1, q2, s); % jtraj使用五次多项式轨迹规划,全程平滑
% 3. 可视化
figure;
Five_dof.plot(q_traj, 'trail', 'g', 'movie', 'jtraj_smooth.gif');
title('jtraj: No More Jumps! Smooth & Safe Motion');核心代码
Matlab
s = linspace(0, 1, 51);
q_traj = jtraj(q1, q2, s); % jtraj使用五次多项式轨迹规划,全程平滑运行效果

飘柔,纵享新丝滑!
这个是因为,
我们先把初末位姿转化为变换矩阵,然后对其逆解得到初末的关节变量,然后对关节变量进行插值,这就使得关节变量连续可微。
写在最后
这节课内容非常多,你可能需要3-4小时来实操和消化,尤其是在笛卡尔空间插值和在关节空间插值二者的区别和效果的理解上。
首先我们明确了轨迹规划的任务,包括了空间规划和时间规划,使用的方法是插值法;
接着我们复习了书上最简单的关节空间的三项式插值,理解了最基本的原理。
接着我们一起学习了时间上是如何控制的,linspace负责控制开始结束和插值点数,
lspb、tpoly负责将其映射到坐标上,完成时间上的插值;
然后我们学习了一个通用的插值方式------mtraj,他负责多维的插值控制,可以选择@空间映射函数。
接着我们学习了笛卡尔空间的空间规划器------trinterp和ctraj。
最后我们发现,当仿真涉及姿态的变换时,前面这些方法都行不通,这是因为笛卡尔空间的连续性经过逆解后无法推得关节空间的连续性,也就是逆解对连续没有传递性。
因此我们想出来用jtraj直接在关节空间插值,彻底解决了这个难题。
你太棒了!