机器人-六轴机械臂的逆运动学

在机器人学领域，逆运动学（Inverse Kinematics, IK）是一个经典而又挑战性的问题。想象一下，你告诉机械臂末端要到达某个特定位置和姿态，机械臂如何知道每个关节应该转动多少角度？这就是逆运动学要解决的问题。

与正运动学（已知关节角求末端位姿）相比，逆运动学更像是解一道复杂的几何代数方程。今天，我将深入探讨六轴机械臂的逆运动学实现，并提供完整的Python代码。

一、为什么逆运动学如此重要？

1.1 实际应用场景

• 路径规划：机械臂需要从A点移动到B点

• 目标抓取：末端执行器需要以特定姿态抓取物体

• 轨迹跟踪：沿预定轨迹移动

• 避障规划：绕过障碍物到达目标位置

1.2 技术挑战

• 多解性：同一末端位姿可能对应多个关节角组合

• 奇异位置：某些位置会导致自由度丢失

• 计算复杂性：需要高效稳定的算法

• 实时性要求：工业应用需要毫秒级响应

二、我的六轴机械臂模型

2.1 D-H参数定义

连杆 i	关节角 qᵢ（°）	连杆偏移 dᵢ（mm）	连杆长度 aᵢ（mm）	连杆扭转角 αᵢ（°）	关节角偏移 offset（°）
1	q₁（变量）	540	0	90	90
2	q₂（变量）	0	-900	0	-90
3	q₃（变量）	0	-900	0	0
4	q₄（变量）	500	0	90	-90
5	q₅（变量）	345	0	-90	0
6	q₆（变量）	175	0	0	0

2.2 机械臂特点

• 结构：典型的6自由度串联机械臂

• 工作空间：半径约2000mm的球形区域

• 关节类型：前三个关节确定位置，后三个关节确定姿态

三、逆运动学求解原理

3.1 整体思路：分而治之

我将逆运动学问题分解为两个子问题：

1. 位置求解（关节1-3）：确定腕部中心位置

2. 姿态求解（关节4-6）：确定末端姿态

3.2 腕部分离技术

关键洞察：最后三个关节轴相交于一点（腕部中心）。这意味着：

• 腕部中心位置仅取决于前三个关节

• 末端姿态由后三个关节调整

# 腕部中心计算
wrist_center = 末端位置 - d[6] * 末端Z轴方向

四、逐步求解算法

4.1 第一步：求解关节1 (θ₁)

关节1决定机械臂在水平面上的旋转：

# 几何关系求解
wx, wy, wz = wrist_center
q1_1 = atan2(wy, wx) - atan2(d[3], sqrt(wx² + wy² - d[3]²))
q1_2 = atan2(wy, wx) - atan2(d[3], -sqrt(wx² + wy² - d[3]²))

物理意义：第一个关节有两个可能方向，对应机械臂的"左手"和"右手"构型。

4.2 第二步：求解关节3 (θ₃)

使用余弦定理求解肘关节：

# 余弦定理
A = -2*a₁*a₂
B = 2*a₂*d₃
D = (距离公式)/2

cos_θ₃ = (D - a₁*d₃) / (a₁² + d₃² + 2*a₁*d₃*cos(θ₁))

肘部配置：θ₃有两个解，对应"肘部向上"和"肘部向下"。

4.3 第三步：求解关节2 (θ₂)

基于已知的θ₁和θ₃：

k₁ = a₁ + a₂*cos(θ₃) + d₃*sin(θ₃)
k₂ = a₂*sin(θ₃) - d₃*cos(θ₃)

θ₂ = atan2(s, r) - atan2(k₂, k₁)

4.4 第四步：求解关节4-6 (θ₄, θ₅, θ₆)

前三个关节确定后，我们计算剩余旋转：

# 计算前三个关节的变换
T₀₃ = T₁ @ T₂ @ T₃

# 计算需要由后三个关节完成的旋转
R₃₆ = R₀₃⁻¹ @ R_target

# 从R₃₆提取ZYZ欧拉角（对应关节4-6）
# 注意：这里假设关节4、5、6的旋转轴分别为Z、Y、Z

欧拉角提取：

if |R₃₆[2,2]| < 1:  # 非奇异情况
    θ₅ = acos(R₃₆[2,2])
    θ₄ = atan2(R₃₆[1,2]/sin(θ₅), R₃₆[0,2]/sin(θ₅))
    θ₆ = atan2(R₃₆[2,1]/sin(θ₅), -R₃₆[2,0]/sin(θ₅))
else:  # 奇异位置（θ₅ = 0 或 π）
    # 此时θ₄和θ₆不能唯一确定
    θ₅ = 0 if R₃₆[2,2] > 0 else π
    θ₄ = 0  # 选择任意值
    θ₆ = atan2(-R₃₆[0,1], R₃₆[0,0])

五、代码实现详解

5.1 核心逆运动学函数

def your_arm_inverse_kinematics(T_target, q_initial=None):
    """
    六轴机械臂逆运动学求解（解析法）
    
    参数：
        T_target: 4x4齐次变换矩阵，目标末端位姿
        q_initial: 初始关节角（弧度），用于选择最接近的解
    
    返回：
        solutions: 所有可能的关节角解列表
    """
    # 完整的求解流程
    # 1. 提取目标位姿
    # 2. 计算腕部中心
    # 3. 求解θ₁（两个解）
    # 4. 对每个θ₁，求解θ₃（两个解）
    # 5. 对每个(θ₁,θ₃)，求解θ₂
    # 6. 求解θ₄,θ₅,θ₆
    # 7. 处理奇异位置
    # 8. 返回所有有效解

5.2 多解处理策略

对于六轴机械臂，最多可能有8个数学解：

• 关节1：2个解（左/右）

• 关节3：2个解（肘上/肘下）

• 关节5：2个解（腕部翻转）

# 实际实现中需要考虑：
# 1. 关节限位：排除超出物理限制的解
# 2. 奇异位置：特殊处理
# 3. 连续性：选择最接近当前姿态的解

5.3 验证机制

def inverse_kinematics_verification(T_target, q_initial=None):
    """
    逆运动学求解并验证
    
    验证步骤：
    1. 求解逆运动学得到关节角
    2. 使用正运动学计算实际位姿
    3. 比较目标位姿和实际位姿
    4. 计算位置误差和姿态误差
    5. 选择误差最小的解
    """

六、算法性能优化

6.1 数值稳定性处理

# 1. 避免除零
if abs(denominator) < 1e-10:
    # 处理奇异情况

# 2. 浮点数精度处理
if abs(value) < 1e-10:
    value = 0

# 3. 角度归一化
angle = (angle + π) % (2*π) - π

6.2 实时性考虑

# 缓存常用计算结果
cos_cache = {}
sin_cache = {}

def fast_cos(theta):
    if theta not in cos_cache:
        cos_cache[theta] = math.cos(theta)
    return cos_cache[theta]

七、完整演示程序

我的程序提供三种模式：

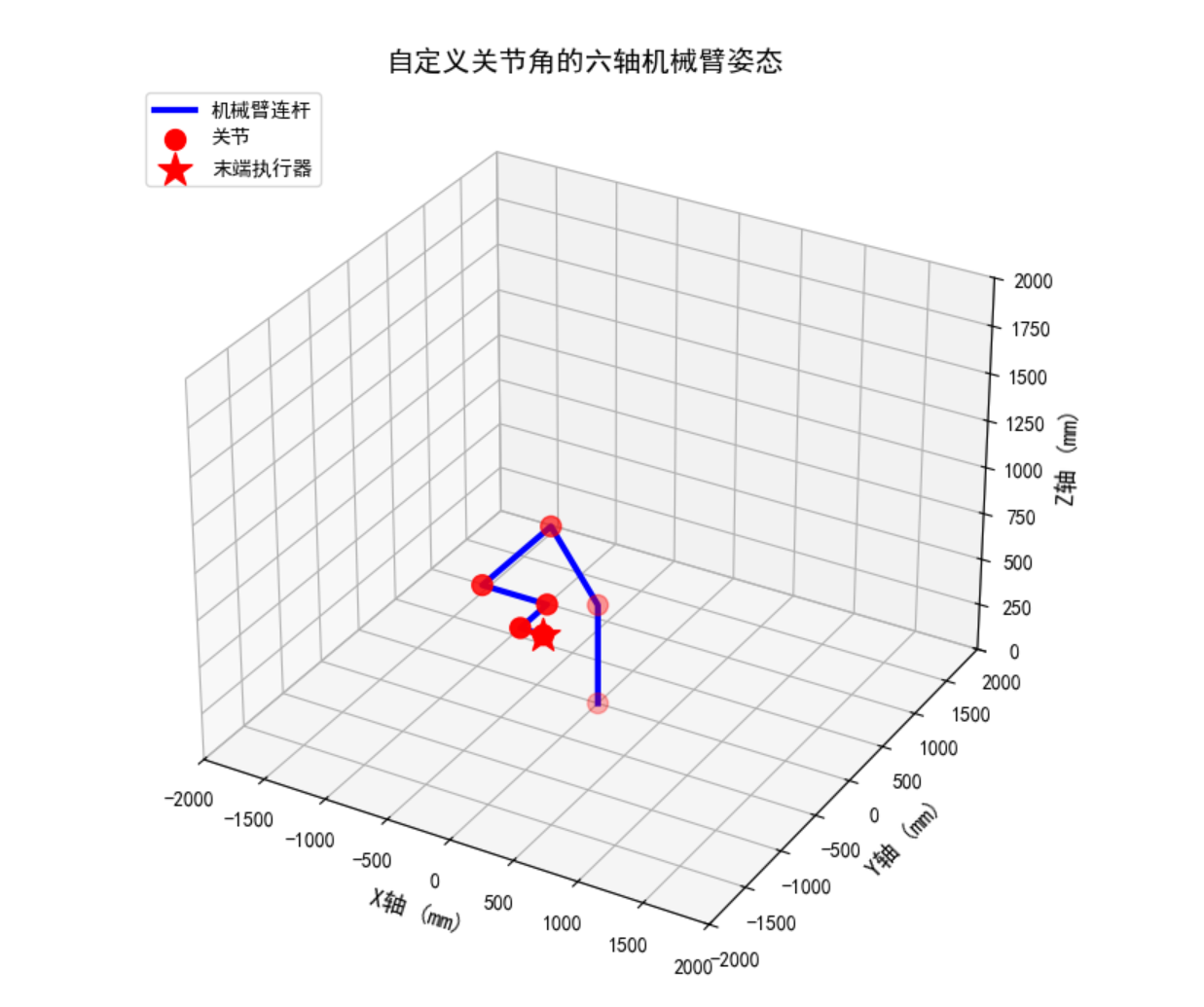
7.1 模式一：正运动学演示

输入：关节角度
输出：机械臂位姿 + 3D可视化

7.2 模式二：逆运动学演示

输入：目标位姿（位置+欧拉角）
输出：关节角度 + 验证误差

7.3 模式三：完整验证

输入：一组关节角度
过程：
  1. 正运动学计算目标位姿
  2. 逆运动学求解关节角度
  3. 比较原始解和求解结果
输出：验证误差 + 可视化

附件（完整代码）：

"""
六轴机械臂逆运动学
基于标准D-H模型，单位：mm（长度）、度（角度）
核心功能：输入末端位姿（齐次变换矩阵），输出所有可行且符合限位的关节角解
"""
import math
import numpy as np

# ========================== 机械臂D-H参数配置 ==========================
# 连杆参数（mm）
d1 = 540.0  # 关节1的连杆偏移
a2 = -900.0  # 关节2的连杆长度
a3 = -900.0  # 关节3的连杆长度
d4 = 500.0  # 关节4的连杆偏移
d5 = 345.0  # 关节5的连杆偏移
d6 = 175.0  # 关节6的连杆偏移

# 关节角偏移（度）：补偿机械臂实际安装的角度偏差
theta_offset = [90.0, -90.0, 0.0, -90.0, 0.0, 0.0]

# ========================== 关节角度限位配置（度）==========================
# 格式：[q1_min, q1_max, q2_min, q2_max, ..., q6_min, q6_max]
JOINT_LIMITS_DEG = [
    -180.0, 180.0,  # q1：基座旋转
    -90.0, 90.0,  # q2：肩部俯仰
    -150.0, 150.0,  # q3：肘部俯仰
    -180.0, 180.0,  # q4：腕部旋转
    -120.0, 120.0,  # q5：腕部俯仰
    -180.0, 360.0  # q6：末端旋转
]

# 常量定义
PI = math.pi
DEG_TO_RAD = PI / 180.0  # 角度转弧度
RAD_TO_DEG = 180.0 / PI  # 弧度转角度
ZERO_THRESH = 1e-10  # 数值计算容差（避免除以0或根号负数）


# ========================== 逆运动学核心类 ==========================
class SixAxisIK:
    def __init__(self):
        """初始化：存储逆解结果"""
        self.solutions_rad = []  # 关节角解（弧度）
        self.solutions_deg = []  # 关节角解（度）
        self.valid_solutions_deg = []  # 符合限位的关节角解（度）
        self.valid_solutions_normalized = []  # 归一化后的有效解（度）

        # 解析关节限位为字典，便于调用
        self.joint_limits = {
            i: (JOINT_LIMITS_DEG[2 * i], JOINT_LIMITS_DEG[2 * i + 1])
            for i in range(6)
        }

    @staticmethod
    def sign(x):
        """符号函数：处理数值正负"""
        return 1 if x > 0 else (-1 if x < 0 else 0)

    @staticmethod
    def clamp_angle_rad(theta):
        """将弧度角限制在[-2π, 2π]范围"""
        while theta < -2 * PI or theta > 2 * PI:
            theta -= SixAxisIK.sign(theta) * 2 * PI
        return theta

    @staticmethod
    def clamp_angle_deg(theta):
        """将角度制角限制在[-360°, 360°]范围"""
        while theta < -360.0 or theta > 360.0:
            theta -= SixAxisIK.sign(theta) * 360.0
        return theta

    @staticmethod
    def normalize_angle_deg(theta):
        """
        将角度归一化到[-180°, 180°]范围（机械臂关节旋转的等效角度）
        :param theta: 原始角度（度）
        :return: 归一化后的角度（度）
        """
        theta = theta % 360.0
        if theta > 180.0:
            theta -= 360.0
        return theta

    def check_joint_limit(self, joint_angle_deg, joint_idx):
        """
        检查单个关节角是否符合限位（考虑角度循环特性）
        :param joint_angle_deg: 关节角（度）
        :param joint_idx: 关节索引（0-5对应q1-q6）
        :return: (是否符合限位, 归一化后的角度)
        """
        min_deg, max_deg = self.joint_limits[joint_idx]
        # 归一化到[-180°, 180°]，体现关节的实际旋转角度
        norm_angle = self.normalize_angle_deg(joint_angle_deg)

        # 特殊处理q6的限位（-180°~360°），不做归一化
        if joint_idx == 5:
            return min_deg <= joint_angle_deg <= max_deg, joint_angle_deg
        else:
            return min_deg <= norm_angle <= max_deg, norm_angle

    def filter_solutions_by_limit(self):
        """筛选符合关节限位的解，并保存归一化后的角度"""
        self.valid_solutions_deg = []
        self.valid_solutions_normalized = []
        for sol in self.solutions_deg:
            is_valid = True
            norm_sol = []
            for idx, angle in enumerate(sol):
                valid, norm_angle = self.check_joint_limit(angle, idx)
                norm_sol.append(norm_angle)
                if not valid:
                    is_valid = False
                    break
            if is_valid:
                self.valid_solutions_deg.append(sol)
                self.valid_solutions_normalized.append(norm_sol)
        return self.valid_solutions_deg, self.valid_solutions_normalized

    @staticmethod
    def euler_to_trans(position, euler_zyx):
        """
        由末端位置和欧拉角生成齐次变换矩阵
        :param position: 末端位置 [x, y, z] (mm)
        :param euler_zyx: 欧拉角 [α, β, γ]（Z-Y-X顺序，度）
        :return: 4x4齐次变换矩阵
        """
        x, y, z = position
        alpha, beta, gamma = [ang * DEG_TO_RAD for ang in euler_zyx]

        # 绕Z轴旋转矩阵
        Rz = np.array([
            [math.cos(alpha), -math.sin(alpha), 0],
            [math.sin(alpha), math.cos(alpha), 0],
            [0, 0, 1]
        ])
        # 绕Y轴旋转矩阵
        Ry = np.array([
            [math.cos(beta), 0, math.sin(beta)],
            [0, 1, 0],
            [-math.sin(beta), 0, math.cos(beta)]
        ])
        # 绕X轴旋转矩阵
        Rx = np.array([
            [1, 0, 0],
            [0, math.cos(gamma), -math.sin(gamma)],
            [0, math.sin(gamma), math.cos(gamma)]
        ])
        # 组合旋转矩阵：R = Rz * Ry * Rx
        R = np.dot(Rz, np.dot(Ry, Rx))

        # 构造齐次变换矩阵
        T = np.eye(4)
        T[:3, :3] = R
        T[:3, 3] = [x, y, z]
        return T

    def solve(self, T):
        """
        逆运动学核心求解：输入末端齐次矩阵，计算所有可行关节角
        :param T: 4x4末端齐次变换矩阵
        :return: 所有解（度），符合限位的解（度），归一化后的有效解（度）
        """
        # 清空历史解
        self.solutions_rad = []
        self.solutions_deg = []
        self.valid_solutions_deg = []
        self.valid_solutions_normalized = []

        # 提取齐次矩阵的旋转轴和位置向量
        n = T[:, 0]  # x轴单位向量
        o = T[:, 1]  # y轴单位向量
        a = T[:, 2]  # z轴单位向量
        p = T[:, 3]  # 位置向量

        # ========================== 步骤1：求解关节1（θ1） ==========================
        m = d6 * a[1] - p[1]
        n_val = d6 * a[0] - p[0]
        r = m ** 2 + n_val ** 2 - d4 ** 2

        theta1_candidates = []
        if r >= -ZERO_THRESH:
            r = max(r, 0)
            sqrt_r = math.sqrt(r)
            theta1_1 = math.atan2(m, n_val) - math.atan2(d4, sqrt_r)
            theta1_2 = math.atan2(m, n_val) - math.atan2(d4, -sqrt_r)
            theta1_candidates = [theta1_1, theta1_2]
        else:
            theta1 = math.atan2(m, n_val)
            theta1_candidates = [theta1]

        # ========================== 步骤2：求解关节5（θ5） ==========================
        theta5_candidates = []
        for theta1 in theta1_candidates:
            temp = a[0] * math.sin(theta1) - a[1] * math.cos(theta1)
            temp = np.clip(temp, -1, 1)
            theta5_1 = math.acos(temp)
            theta5_2 = -math.acos(temp)
            theta5_candidates.append([theta1, theta5_1])
            theta5_candidates.append([theta1, theta5_2])

        # ========================== 步骤3：求解关节6（θ6） ==========================
        theta6_candidates = []
        for theta1, theta5 in theta5_candidates:
            m = n[0] * math.sin(theta1) - n[1] * math.cos(theta1)
            n_val = o[0] * math.sin(theta1) - o[1] * math.cos(theta1)
            theta6 = math.atan2(m, n_val) - math.atan2(math.sin(theta5), 0)
            theta6_candidates.append([theta1, theta5, theta6])

        # ========================== 步骤4：求解关节3（θ3） ==========================
        theta3_candidates = []
        for theta1, theta5, theta6 in theta6_candidates:
            c1 = math.cos(theta1)
            s1 = math.sin(theta1)
            c6 = math.cos(theta6)
            s6 = math.sin(theta6)

            m = d5 * (s6 * (n[0] * c1 + n[1] * s1) + c6 * (o[0] * c1 + o[1] * s1)) - d6 * (a[0] * c1 + a[1] * s1) + p[
                0] * c1 + p[1] * s1
            n_val = p[2] - d1 - a[2] * d6 + d5 * (o[2] * c6 + n[2] * s6)

            m2_n2 = m ** 2 + n_val ** 2
            denominator = 2 * a2 * a3
            if abs(denominator) < ZERO_THRESH:
                continue

            cos_theta3 = (m2_n2 - a2 ** 2 - a3 ** 2) / denominator
            cos_theta3 = np.clip(cos_theta3, -1, 1)
            theta3_1 = math.acos(cos_theta3)
            theta3_2 = -math.acos(cos_theta3)
            theta3_candidates.append([theta1, theta5, theta6, theta3_1])
            theta3_candidates.append([theta1, theta5, theta6, theta3_2])

        # ========================== 步骤5：求解关节2（θ2） ==========================
        theta2_candidates = []
        for theta1, theta5, theta6, theta3 in theta3_candidates:
            c1 = math.cos(theta1)
            s1 = math.sin(theta1)
            c6 = math.cos(theta6)
            s6 = math.sin(theta6)
            c3 = math.cos(theta3)
            s3 = math.sin(theta3)

            m = d5 * (s6 * (n[0] * c1 + n[1] * s1) + c6 * (o[0] * c1 + o[1] * s1)) - d6 * (a[0] * c1 + a[1] * s1) + p[
                0] * c1 + p[1] * s1
            n_val = p[2] - d1 - a[2] * d6 + d5 * (o[2] * c6 + n[2] * s6)

            denominator = a2 ** 2 + a3 ** 2 + 2 * a2 * a3 * c3
            if abs(denominator) < ZERO_THRESH:
                continue

            s2 = ((a3 * c3 + a2) * n_val - a3 * s3 * m) / denominator
            c2 = (m + a3 * s3 * s2) / (a3 * c3 + a2)
            theta2 = math.atan2(s2, c2)
            theta2_candidates.append([theta1, theta2, theta3, theta5, theta6])

        # ========================== 步骤6：求解关节4（θ4） ==========================
        for theta1, theta2, theta3, theta5, theta6 in theta2_candidates:
            c1 = math.cos(theta1)
            s1 = math.sin(theta1)
            c6 = math.cos(theta6)
            s6 = math.sin(theta6)

            numerator = -s6 * (n[0] * c1 + n[1] * s1) - c6 * (o[0] * c1 + o[1] * s1)
            denominator = o[2] * c6 + n[2] * s6
            if abs(denominator) < ZERO_THRESH:
                continue

            theta4 = math.atan2(numerator, denominator) - theta2 - theta3
            self.solutions_rad.append([theta1, theta2, theta3, theta4, theta5, theta6])

        # ========================== 结果处理 ==========================
        for sol_rad in self.solutions_rad:
            sol_deg = []
            for i in range(6):
                theta_rad = sol_rad[i] - theta_offset[i] * DEG_TO_RAD
                theta_deg = self.clamp_angle_deg(theta_rad * RAD_TO_DEG)
                sol_deg.append(theta_deg)
            self.solutions_deg.append(sol_deg)

        # ========================== 筛选符合限位的解 ==========================
        self.filter_solutions_by_limit()

        return self.solutions_deg, self.valid_solutions_deg, self.valid_solutions_normalized


# ========================== 测试代码 ==========================
if __name__ == "__main__":
    ik_solver = SixAxisIK()

    # 定义末端位姿
    target_pos = [675.0, -1800.0, 1100.0]
    target_euler = [0.0, 90.0, 0.0]

    # 生成齐次变换矩阵
    T_target = ik_solver.euler_to_trans(target_pos, target_euler)
    print("=" * 60)
    print("目标末端齐次变换矩阵：")
    print(np.round(T_target, 3))

    # 求解逆运动学
    all_solutions, valid_solutions, valid_normalized = ik_solver.solve(T_target)

    # 输出所有解
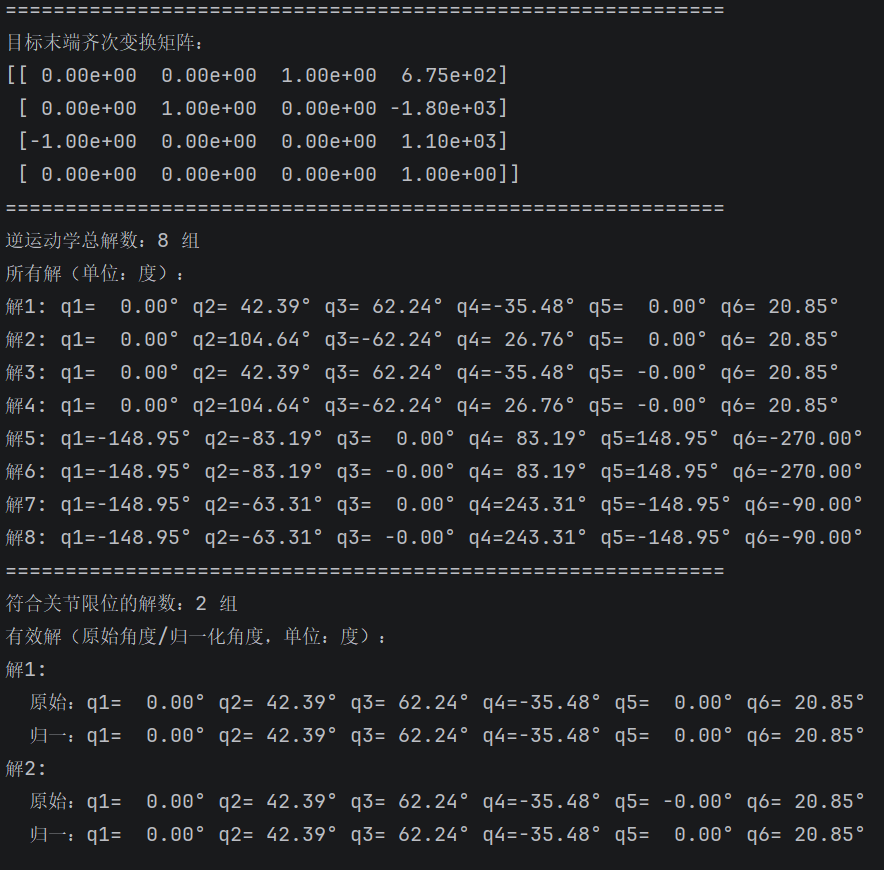
    print("=" * 60)
    print(f"逆运动学总解数：{len(all_solutions)} 组")
    if len(all_solutions) > 0:
        print("所有解（单位：度）：")
        for i, sol in enumerate(all_solutions):
            print(
                f"解{i + 1}: q1={sol[0]:6.2f}° q2={sol[1]:6.2f}° q3={sol[2]:6.2f}° q4={sol[3]:6.2f}° q5={sol[4]:6.2f}° q6={sol[5]:6.2f}°")

    # 输出有效解（含归一化角度）
    print("=" * 60)
    print(f"符合关节限位的解数：{len(valid_solutions)} 组")
    if len(valid_solutions) > 0:
        print("有效解（原始角度/归一化角度，单位：度）：")
        for i, (sol, norm_sol) in enumerate(zip(valid_solutions, valid_normalized)):
            print(f"解{i + 1}:")
            print(
                f"  原始：q1={sol[0]:6.2f}° q2={sol[1]:6.2f}° q3={sol[2]:6.2f}° q4={sol[3]:6.2f}° q5={sol[4]:6.2f}° q6={sol[5]:6.2f}°")
            print(
                f"  归一：q1={norm_sol[0]:6.2f}° q2={norm_sol[1]:6.2f}° q3={norm_sol[2]:6.2f}° q4={norm_sol[3]:6.2f}° q5={norm_sol[4]:6.2f}° q6={norm_sol[5]:6.2f}°")
    else:
        print("警告：无符合关节限位的解！")

    # 测试末端位姿
    target_pos = [675.0, -1800.0, 1100.0]
    target_euler = [0.0, 90.0, 0.0]

运行实例：