LeetCode 24 两两交换链表中的节点（ 迭代与递归）

LeetCode 24 两两交换链表中的节点（图解 + 迭代与递归）

### 文章目录

• [LeetCode 24 两两交换链表中的节点（图解 + 迭代与递归）](#文章目录 LeetCode 24 两两交换链表中的节点（图解 + 迭代与递归） @[toc] 题目 思路总览 迭代解法 C++ Python 递归解法 C++ Python 易错点与排坑 测试用例 复杂度对比与选择 总结)
• [@[toc]](#文章目录 LeetCode 24 两两交换链表中的节点（图解 + 迭代与递归） @[toc] 题目 思路总览 迭代解法 C++ Python 递归解法 C++ Python 易错点与排坑 测试用例 复杂度对比与选择 总结)
• [题目](#文章目录 LeetCode 24 两两交换链表中的节点（图解 + 迭代与递归） @[toc] 题目 思路总览 迭代解法 C++ Python 递归解法 C++ Python 易错点与排坑 测试用例 复杂度对比与选择 总结)
• [思路总览](#文章目录 LeetCode 24 两两交换链表中的节点（图解 + 迭代与递归） @[toc] 题目 思路总览 迭代解法 C++ Python 递归解法 C++ Python 易错点与排坑 测试用例 复杂度对比与选择 总结)
• [迭代解法](#文章目录 LeetCode 24 两两交换链表中的节点（图解 + 迭代与递归） @[toc] 题目 思路总览 迭代解法 C++ Python 递归解法 C++ Python 易错点与排坑 测试用例 复杂度对比与选择 总结)
• [C++](#文章目录 LeetCode 24 两两交换链表中的节点（图解 + 迭代与递归） @[toc] 题目 思路总览 迭代解法 C++ Python 递归解法 C++ Python 易错点与排坑 测试用例 复杂度对比与选择 总结)
• [Python](#文章目录 LeetCode 24 两两交换链表中的节点（图解 + 迭代与递归） @[toc] 题目 思路总览 迭代解法 C++ Python 递归解法 C++ Python 易错点与排坑 测试用例 复杂度对比与选择 总结)
• [递归解法](#文章目录 LeetCode 24 两两交换链表中的节点（图解 + 迭代与递归） @[toc] 题目 思路总览 迭代解法 C++ Python 递归解法 C++ Python 易错点与排坑 测试用例 复杂度对比与选择 总结)
• [C++](#文章目录 LeetCode 24 两两交换链表中的节点（图解 + 迭代与递归） @[toc] 题目 思路总览 迭代解法 C++ Python 递归解法 C++ Python 易错点与排坑 测试用例 复杂度对比与选择 总结)
• [Python](#文章目录 LeetCode 24 两两交换链表中的节点（图解 + 迭代与递归） @[toc] 题目 思路总览 迭代解法 C++ Python 递归解法 C++ Python 易错点与排坑 测试用例 复杂度对比与选择 总结)
• [易错点与排坑](#文章目录 LeetCode 24 两两交换链表中的节点（图解 + 迭代与递归） @[toc] 题目 思路总览 迭代解法 C++ Python 递归解法 C++ Python 易错点与排坑 测试用例 复杂度对比与选择 总结)
• [测试用例](#文章目录 LeetCode 24 两两交换链表中的节点（图解 + 迭代与递归） @[toc] 题目 思路总览 迭代解法 C++ Python 递归解法 C++ Python 易错点与排坑 测试用例 复杂度对比与选择 总结)
• [复杂度对比与选择](#文章目录 LeetCode 24 两两交换链表中的节点（图解 + 迭代与递归） @[toc] 题目 思路总览 迭代解法 C++ Python 递归解法 C++ Python 易错点与排坑 测试用例 复杂度对比与选择 总结)
• [总结](#文章目录 LeetCode 24 两两交换链表中的节点（图解 + 迭代与递归） @[toc] 题目 思路总览 迭代解法 C++ Python 递归解法 C++ Python 易错点与排坑 测试用例 复杂度对比与选择 总结)

题目

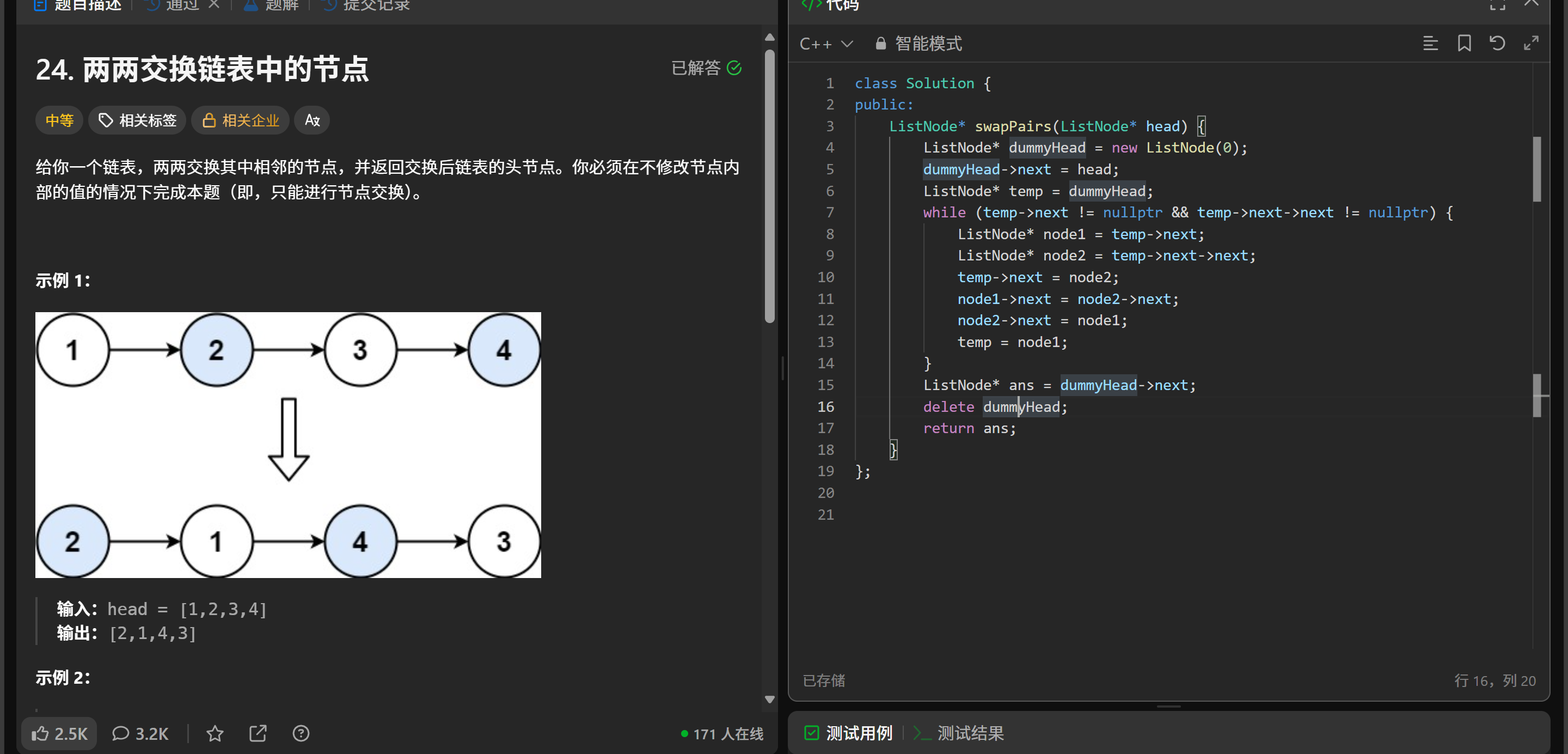
给定一个链表，两两交换其中相邻的节点，并返回交换后的头节点。必须在不修改节点内部值的情况下完成交换（即只能进行节点交换）。

• 原题链接：LeetCode 24. Swap Nodes in Pairs
• 难度：中等

---

思路总览

• 交换单位：以一对一对节点为单位：first 和 second。
• 连线顺序（关键）：
  1. prev->next = second
  2. first->next = second->next
  3. second->next = first
• 移动指针：完成一对交换后，prev 移动到 first（交换后的第二个），继续处理下一对。
• 处理边界：
  • 空链表或单节点直接返回。
  • 哑节点 dummy 简化头结点被交换的连接逻辑。

---

迭代解法

C++

// Definition for singly-linked list.
struct ListNode {
    int val;
    ListNode *next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *next) : val(x), next(next) {}
};

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        ListNode dummy(0);
        dummy.next = head;
        ListNode* prev = &dummy;
        while (prev->next && prev->next->next) {
            ListNode* first = prev->next;
            ListNode* second = first->next;

            // 1) prev -> second
            prev->next = second;
            // 2) first -> second->next
            first->next = second->next;
            // 3) second -> first
            second->next = first;

            // 移到下一对的前驱
            prev = first;
        }
        return dummy.next;
    }
};

Python

from typing import Optional

class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

class Solution:
    def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:
        dummy = ListNode(0, head)
        prev = dummy
        while prev.next and prev.next.next:
            first = prev.next
            second = first.next

            prev.next = second
            first.next = second.next
            second.next = first

            prev = first
        return dummy.next

• 时间复杂度：O(n)
• 空间复杂度：O(1)

---

递归解法

递归天然按"每次处理两个节点"展开：

1. 递归处理 head->next->next 作为后续链；
2. 交换当前的 head 与 head->next；
3. 返回新的子头节点。

C++

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if (!head || !head->next) return head;
        ListNode* first = head;
        ListNode* second = head->next;
        // 递归交换后续
        first->next = swapPairs(second->next);
        // 当前二者交换
        second->next = first;
        return second;
    }
};

Python

class Solution:
    def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:
        if not head or not head.next:
            return head
        first, second = head, head.next
        first.next = self.swapPairs(second.next)
        second.next = first
        return second

• 时间复杂度：O(n)
• 空间复杂度：O(n)（递归调用栈）

---

易错点与排坑

• 忘记保存 second->next 导致链断。
• 交换后 prev 的移动位置应为 first（交换后的后者）。
• 没有使用哑节点，导致头结点被交换时连接逻辑复杂、易错。
• 递归写法中要先递归连接后续，再完成当前交换。

---

测试用例

输入：head = [1,2,3,4]
输出：[2,1,4,3]

输入：head = []
输出：[]

输入：head = [1]
输出：[1]

输入：head = [1,2,3]
输出：[2,1,4,3] 中的前两对，注意最后一个单独节点保留为 3（结果 [2,1,3]）

---

复杂度对比与选择

• 迭代：O(n)/O(1)，推荐，工程上更稳。
• 递归：O(n)/O(n)，思路更直观，但要注意栈深度。

---

总结

• 模板化三步连线是本题关键，配合 dummy 指针可无脑套用。
• 面试建议先写迭代版，再口述/补充递归版，展示对指针与递归的掌握。